基于Dijkstra算法的校园外卖配送方案

Campus Delivery Scheme Based on Dijkstra Algorithm

摘要: 近几年，随着科技的发展以及人们的生活水平提高，外卖这个新兴行业正在蓬勃发展，其中发展最快的莫过于是校园外卖。本文通过对校园外卖最短路线问题的优化求解，将校园内的外卖配送问题等效转化为最短路线问题，并运用Dijkstra算法求得校园外卖的最佳配送方案，编制了MATLAB程序，确定了校园外卖派送的最短路线。最后，通过实验算例验证了本文算法的有效性和可行性。

Abstract: In recent years, with the development of science and technology and the improvement of people’s living standards, the emerging industry of take-out is developing rapidly, among which the fastest development is campus take-out. In this paper, by solving the problem of the shortest route of campus take-out, the problem of the delivery of campus take-out is equivalent to the shortest route problem. Dijkstra algorithm was used to obtain the best delivery scheme of campus take-out, and MATLAB program was compiled to determine the shortest route of campus take-out delivery. Finally, the validity and feasibility of the proposed algorithm are verified by an experimental example.

1. 引言

近两年，随着电子商务的兴起以及送货上门服务的发展 [1] ，电子商务已经渗透到了我们生活的方方面面，校园外卖的迅速崛起就是最好的证明。由于恶劣天气、课业繁重、睡眠不足等等原因，越来越多的同学不想起身去餐厅吃饭，他们通常会选择订外卖的方式来节约时间。对饥饿的同学来说，最希望的就是外卖能够准时到达，但是由于商家配送外卖的数量多、宿舍楼分布错乱等问题，外卖常常不能够按时送达。所以，合理规划外卖路线是十分重要的，这样不仅可以为商家留住客户，更可以为商家送出更多的外卖，节省了运输成本，使商家获得更多的利润。我们通过对最短路线的研究，将外卖配送路线问题转化为最短路线问题进行研究。目前，国内外的专家学者对最短路线的问题也进行了较为深入的研究。比如，王树西等 [2] 分析了多邻接点问题与多条最短路径问题的成因对Dijkstra算法进行了改进；周康等 [3] 给出了固定端点的最短路问题闭环DNA算法；赵礼峰等 [4] 通过迭代矩阵和下标标注法对Floyd算法进行了改进,改进后的算法能快速地计算出网络中任意两节点之间的最短路长值；冯树民等 [5] 为了简化多目标最短路算法的问题，利用理想点法的优点，探索出一种多目标最短路问题的简便算法；丁秋雷，胡祥培等 [6] 针对干扰事件导致物流配送难以顺利实施这一难题，提出基于前景理论的扰动度量方法进行求解。本文根据Dijkstra算法的思想并在此基础上做出了改进，Dijkstra算法是保证源点到各个顶点之间的路程最短的求解最短路线的方法，而改进后的算法是在保证经过所有顶点的前提下，使得总的路线最短，这样就对外卖配送路线问题给出了优化设计方案，给出了算法步骤，并编制出了MATLAB程序。

2. 模型建立

在校园外卖配送过程中，按时到达是一件非常重要的事。而按时到达，取决于骑手配送外卖的速度。当外卖骑手最大速度一定的情况下，路线越短，配送的速度就越快。

由于校园外卖有如下几个特点：

1) 区域密集性。学生宿舍一般是聚集在某个区域内，宿舍楼在区域内密集分布。

2) 时间确定性。订餐时间一般在从午九点到下午一点、下午五点到七点。

3) 路线复杂性。各宿舍楼之间的连通的路线繁复。。

这就意味着，外卖骑手需要在一个固定的时间、一块密集的宿舍楼区域、一段曲折蜿蜒、岔路丛生的路上配送尽可能多的外卖。倘若走错了一个路口，那很可能需要绕一圈路才能到达目的地。

由此带来的不仅是顾客的不满、骑手的金钱损失、甚至于商家的信誉损失。所以给出一条从商家到客户的最短路线是十分重要的。

现给出一个以起点(1)为起始点的有向图图G，如图1所示。

其中，在有向图图G中，存在n个连接点与m条连接各点的路径，在图一的所有路径中，不同路径有不同的权值，寻找以起点(1)为起始点，连接其余 $\left(n-1\right)$ 个点的最短路径。

本文根据两种不同情况下提出求解最短路径的方法：

1) 单条路径最短路线求解，在图1中寻找一条路径经过其中所有的连接点，使得求得最短路径的权值和最小。

2) 多条路径最短路线求解，在图1中寻找多条路径经过其中所有的连接点，使得求得最短路径的权值和最小。

2.1. 单条路径最短路线求解(附录1)

已知起始点的位置是固定的，由起始点开始由一条最短路径连接剩下的连接点.在已知相互各点之间的权值的情况下，找出与起始点权值最小的连接点 $i$ ，然后再以 $i$ 点为起始点找出与它相连的权值最小的连接点，以上述规则进行迭代，每次都选取最小的权值，最终所形成的路径的权值也会是最小的，即最短路线.下面利用矩阵的形式表示上述方案：

Step 1：将各点之间的权值在矩阵中表示出来， $a_{ij}$ 为 $i$ 点与 $j$ 点之间的权值，由此建立一个 $n\times n$ 的矩阵 $A$ 。

$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right)$

其中，矩阵 $A$ 中当 $a_{ii}\left(i=j\right)$ 时表示的为自身之间的距离，为避免对结果造成影响，故设为无穷大数，即 $a_{ii}=\infty$ 。

Step 2：比较矩阵 $A$ 的第一列，得出第一列的最小值 $a_{1k}$ ，即与起始点相连的点中， $k$ 点与起始点之间的权值最小。

Step 3：再以 $k$ 点为起点，找与 $k$ 点之间权值最小的点。在矩阵 $A$ 的第 $k$ 行，比较 $k$ 行中各个元素的大小，可得第 $k$ 行中最小的元素为 $a_{km}$ ，其含义为 $k$ 点与 $m$ 点之间的权值最小。输出点 $m$ ，将元素 $a_{km}$ 所在的列上所有的元素都变为无穷大值，得到矩阵 $B$ 。

$B=\left(\begin{array}{ccccccc}{a}_{11}& \cdots & a_{1\left(m-1\right)}& \infty & a_{1\left(m+1\right)}& \cdots & a_{1n}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{k1}& \cdots & a_{k\left(m-1\right)}& \infty & a_{k\left(m+1\right)}& \cdots & a_{kn}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{n1}& \cdots & a_{n\left(m-1\right)}& \infty & a_{n\left(m+1\right)}& \cdots & a_{nn}\end{array}\right)$

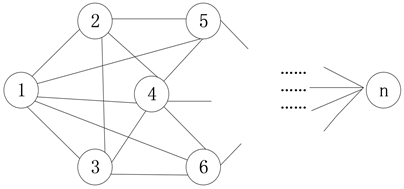
Figure 1. Directed graph with starting point (1) as the starting point

图1. 以起点(1)为起始点的有向图图G

Step 4：以点m为起点，依照第三步的步骤进行迭代，直至路线经历所有点。根据依次输出的值的列序号就能得出单条路径情况下的最短路线。

本方案是基于迭代思想并且运用矩阵给出的算最短路径的方法，该方法简单易懂，过程相对简单，不过对于计算机要求较高，运算起来较为麻烦，对前期数据要求较为具体，但是也从迭代的方面提出了最短路径的算法。

2.2. 多条路径最短路线求解(附录2)

对于该问题的求解，我们给出两种成熟且稳定的算法：

1) 枚举法

枚举法是指找出连接上述 $n$ 个点的所有路径，分别求出每条路径的权值，最后比较各条路径的权值

大小，从而找出最短路径。但是连接各点路径最多将会有 $\frac{n\left(n-1\right)}{2}$ 条，当 $n$ 很大时，利用枚举法将会耗费大量的时间和精力。

2) Dijkstra法

Dijkstra法是一种基于矩阵和集合的思想来求最短路径的方法，具体步骤如下：

Step 1：创立两个集合 $U,V$ ，其中 $U$ 集合存放源点，指路径出发的点， $V$ 集合存放待定点，指路径到达的终点。

Step 2：比较各源点与待定点之间的权值，将权值最小的两点连线，将此待定点加入源点集合 $U$ 。

Step 3：重复第二步，直到待定点全部加入源点集合 $U$ 。待定点加入源点集合的顺序即路径行走的顺序。

接下来我们通过矩阵形式来表示上述过程：

首先，我们先提出两个假设：

①假设不存在孤立点，各连接点至少由一条路径与其他连接点相连；

②自身与自身相连表示权值为无穷，两点之间不相连表示权值为无穷。

根据假设，图1可用矩阵表示为

$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right)$

其中 $a_{ii}=\infty ,\left(i=1,2\cdots n\right)$ ， $a_{ij}=a_{ji}$ ， $a_{ij}$ 表示为 $i,j$ 两点之间的权值。

①在矩阵 $A$ 中找到源点所对应的行向量 $S$ 。如以点1为源点，源点矩阵 $S=\left[a_{11}{a}_{12}\cdots a_{1n}\right]$ 。

②在源点矩阵 $S$ 寻找权值最小的 $a_{ij}$ ，其中 $i$ 为源点， $j$ 为待定点。

③将 $j$ 点对应的行向量加入源点矩阵 $S$ ， $S=\left[\begin{array}{l}{a}_{11}{a}_{12}\cdots a_{1n}\\ a_{j1}{a}_{j2}\cdots a_{jn}\end{array}\right]$ ，在其中以无穷大替换步骤②找出的最

小值 $a_{ij}$ 。

对源点矩阵 $S$ 循环实行②③步，直至源点矩阵 $S$ 的维数与矩阵 $A$ 相同。待定点加入源点矩阵的顺序即路径行走的顺序。

2.3. 算法比较

枚举法与迪杰斯特拉法相比，过程清晰，结果精确度高，原理简单明了，可一旦连接点的个数变多，运算过程就会变得冗杂、繁复、实际应用时问题很大。Dijkstra法的好处在于不需要数据运算，只需要进行简单的比较就能得出结果，并且能够剔除已知的结果，使得下一步过程进一步简化。由此可知，在面对实际应用时，Dijkstra法能够快速的找到最佳的多条路径最短路线方案。

3. 数值算例

某学校有五座宿舍楼，外卖商家与五座宿舍楼不在一处。已经给出五座宿舍楼之间的距离和五座宿舍楼与商家的距离，如表1所示。假设骑手的配送速度固定，现要求给出两种方案，一种是当只有一个外卖骑手配送外卖时的最短路线；另一种是由多位外卖骑手共同配送外卖时的最短路线。上述两种方案中，要求骑手经过所有宿舍楼且配送外卖的时间最短。

已知骑手的速度 $v$ 一定，要求找出最佳方案，使得骑手配送外卖的时间 $t$ 最短。再由简单的物理知识

路程(s) = 时间(t) × 速率(v)可知：“ $t=\frac{s}{v}$ ”，即配送路线距离越小，配送外卖所用的时间越短。由此，

将最短时间问题转化为最短路线问题。

假设外卖骑手的配送速度为 $v$ ，配送时间为 $t$ ，配送路线距离为 $s$ ，其中配送速度已知。由于

$t=t\left(s,v\right)=\frac{s}{v}$ ，故求出最短路线的距离 $s$ 即可。

Step 1：作出路线图

根据表1的数据，做出路线图，如图2所示。

Table 1. The distance between any two points

表1. 任意两地点之间的距离

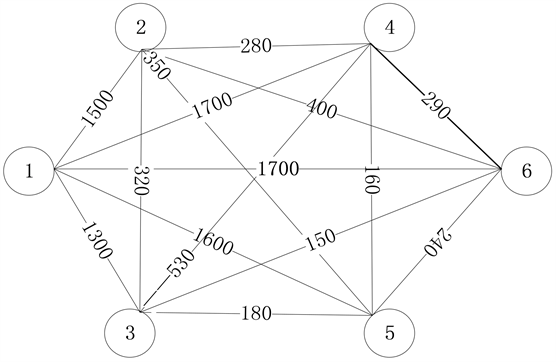
Figure 2. A road map from known data

图2. 由已知数据得出的路线图

Step 2：将表1使用矩阵的形式表述

$A=\left(\begin{array}{cccccc}0& 1500& \text{1300}& \text{1700}& \text{1600}& \text{1800}\\ 1500& 0& 320& 280& 350& 400\\ 1300& 320& 0& 530& 180& 150\\ 1700& 280& 530& 0& 160& 290\\ 1600& 350& 180& 160& 0& 240\\ 1800& 400& 150& 290& 240& 0\end{array}\right)$

为了使得运算过程简单方便，在此采取两个小技巧，规定自己本身相连的距离为无穷 $a_{ii}=\infty ,\left(i=1,2\cdots n\right)$ ；若两座宿舍楼不直接相连，规定它们之间的距离为无穷，矩阵变为：

$A=\left(\begin{array}{cccccc}\propto & 1500& \text{1300}& \text{1700}& \text{1600}& \text{1800}\\ 1500& \propto & 320& 280& 350& 400\\ 1300& 320& \propto & 530& 180& 150\\ 1700& 280& 530& \propto & 160& 290\\ 1600& 350& 180& 160& \propto & 240\\ 1800& 400& 150& 290& 240& \propto \end{array}\right)$

Step 3：最短路线求解

①单人配送外卖方案

通过单条最短路径求解中求解原理编译的MATLAB程序 $\left[U,V,d\right]=lcxz(A)$

可直接解得

$U=\left[\text{01300150240160280}\right]$ ， $V=\left[\text{136542}\right]$ ， $d=2130$

其中，矩阵 $U$ 储存每一步迭代过程取出的最小值；矩阵 $V$ 储存每步迭代取出的连接点，并且连接点的顺序就是最短路径的顺序； $d$ 为最短路径的长度。

具体路线图如图3所示

②多人配送外卖方案

通过多条最短路径求解中Dijkstra法的求解原理编译的MATLAB程序 $\left[U,V,d\right]=ndjtslA$

可直接解得

$U=\left[\text{01300150180160280}\right]$ ， $V=\left[\text{136542}\right]$ ， $d=2070$

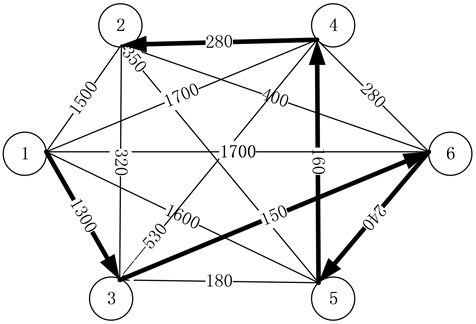
Figure 3. The shortest route to deliver take-out by one person

图3. 单人配送外卖的最短路线方案

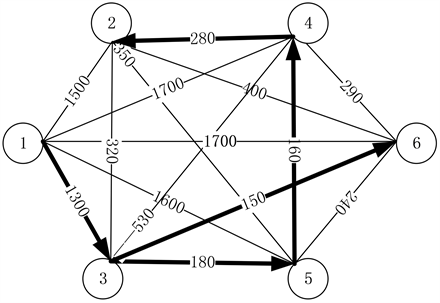
Figure 4. The shortest route to delivery take-out by many people

图4. 多人配送外卖的最短路线方案

其中，矩阵 $U$ 储存每一步迭代过程取出的最小值；矩阵 $V$ 储存每步迭代取出的连接点，并且连接点的顺序就是最短路径的顺序； $d$ 为最短路径的长度。

具体路线图如图4所示。

附录

附录1：单人配送外卖方案MATLAB程序

function [U,V,d]=lcxz(A)

b=inf;

B=A;

U=zeros(1,n);

V=ones(1,n);

R=b*ones(1,n);

L=b*ones(m,1);

a=A(1,:);

B(1,:)=R;

B(:,1)=L;

t=1;

U(1,2)=u;

V(1,2)=v;

for i=2:n-1%循环计算经过路径

s=v;

f=B(v,:);

t=i+t;

U(1,i+1)=u;

V(1,i+1)=v;

B(s,:)=R;

B(:,s)=L;

i=i+1;

end

U;%存储最短两点之间的权值

V;%存储最短路线经过的节点

d=sum(U);%最短路线的总距离

附录2：多人配送外卖方案MATLAB程序

function [U,V,d]=ndjtsl(A)

b=inf;

C=inf*ones(n);

B=A;

U=zeros(1,n);

V=ones(1,n);

rep=b;

a=B(1,:);

B(1,v)=rep;

B(v,1)=rep;

U(1,2)=u;

V(1,2)=v;

f=B(1,:);

for i=3:n %循环计算经过路径

r=v;

F=[f;B(v,:)];

rv=v;

U(1,i)=u;

x=v;

s=V(x);

y=rv(v);

v=y;

V(1,i)=y;

B(r,y)=rep;

B(y,r)=rep;

B(s,y)=rep;

B(y,s)=rep;

f=[f;B(r,:)];

f(x,y)=rep;

i=i+1;

end

U;%存储最短两点之间的权值

V;%存储最短路线经过的节点

d=sum(U);%最短路线的总距离