油气产量预测的GM(1,1)幂模型

GM(1,1) Power Model for Prediction of Oil and Gas Production

摘要: Arps递减模型是目前应用最广的油气产量预测模型，但对测试序列要求高。GM(1,1)幂模型能适应多种形状序列的建模预测。根据二者形式上的相似性，将GM(1,1)幂模型看成Arps模型的扩展。利用GM(1,1)幂模型推导了产量及产量递减率预测公式，建立以误差最小为目标的优化模型求解参数，并利用粒子群算法求解。通过实例证明：利用GM(1,1)幂模型进行产量预测，建模精度更高，适用范围更广。

Abstract: Arps decline model was the most widely used model for predicting oil and gas production at present, but it had a high requirement for test sequences. The GM(1,1) power model was appro-priate for the modeling forecast of multiform sequence. Based on the similarity between the Arps decline model and GM(1,1) power model, this paper regards the GM(1,1) power model as the extension of the Arps decline model. The GM(1,1) power model was taken as the expansion of Arps model; the GM(1,1) power model was used to deduce the predicting formulae of production and production decline rate, and build the optimization model with the objective function that the error was minimal and the particle swarm optimization algorithm was used to solve the problem. It is proved by examples that the modeling accuracy is higher and the range of application is wider by using GM(1,1) power model to predict output.

1. 引言

油气产量预测是油气田制定长期规划的主要依据。由于影响油气产量的因素众多，这给建立理论模型带来一定的困难。根据系统分析的原理，利用生产数据进行建模预测是目前被广泛采用的方法，其中选择科学合理的模型是研究的重点。在20世纪90年代及以前，就已经提出了多种预测模型，例如Arps模型 [1] 、翁氏模型 [2] 、t模型 [3] 、Weibull模型、贝塔旋回模型 [4] 、HCZ模型、伽马旋回模型等一系列模型。但目前在现场应用最广的仍是Arps模型 [5] [6] [7]。但Arps模型选择标准曲线受主观因素影响大，尤其对于非光滑序列，选择初始递减率和递减指数困难，误差大。随着计算机技术的发展，智能算法也逐渐被用来预测油气产量，例如神经网络算法、遗传算法等 [8] [9] [10]。但智能算法需要样本量大，对于少数据的情况难以推广应用。

油气田产量影响因素错综复杂，因此油气生产系统可以看成一个不确定系统。针对该系统“小样本”、“贫信息”的特征，灰色预测模型也在产量预测中得到广泛应用。相对GM(1,1)模型，GM(1,1)幂模型可以满足更多形状序列的模拟 [11]。笔者在分析Arps产量递减模型的基础上，采用GM(1,1)幂模型进行油气产量和产量递减率预测，取得了很好的效果。

2. Arps产量递减模型

Arps产量递减模型是目前应用最广的一种模型，该模型形式如下：

$\frac{a}{a_{\text{i}}}={\left(\frac{Q}{Q_{\text{i}}}\right)}^n$ (1)

式中：a、 $a_{\text{i}}$ 分别为时间t和初始时刻的产量递减率，mon⁻¹或a⁻¹，表示单位时间内产量的变化率。定义式为：

$a=-\frac{1}{Q}\cdot \frac{\text{d}Q}{\text{d}t}$ (2)

式中：Q、 $Q_{\text{i}}$ 分别为时间t和初始时刻的产量，单位是t/mon或t/a；n为递减指数，当 $n=0$ 时称为指数递减；当 $n=1$ 时称为调和递减；当 $n=0.5$ 时称为产量衰减；当 $0<n<1$ 且 $n\ne 0.5$ 时称为双曲递减。该次研究不考虑指数递减，即取 $0<n\le 1$ 。

联立式(1)和式(2)可以得到：

$\text{d}Q=-\frac{a_{\text{i}}}{Q_{\text{i}}^n}\cdot Q^{n+1}\text{d}t$ (3)

取递减初始条件， $t=0$ 时 $Q=Q_{\text{i}}$ ，则可以得到产量和递减率随时间变化的公式：

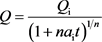(4)

$a=\frac{a_{\text{i}}}{1+n{a}_{\text{i}}t}$ (5)

如果令 $B=-\frac{a_{\text{i}}}{Q_{\text{i}}^n}$ ， $m=n+1$ ，则式(3)可以写为：

$\frac{\text{d}Q}{\text{d}t}=B{Q}^m$ (6)

3. GM(1,1)幂模型

设 $Q^{\left(1\right)}$ 为原始产量序列， $Q^{\left(1\right)}=\left(Q^{\left(1\right)}\left(1\right),Q^{\left(1\right)}\left(2\right),\cdots ,Q^{\left(1\right)}\left(k\right)\right)$ ， $Q^{\left(0\right)}=\left(Q^{\left(0\right)}\left(1\right),Q^{\left(0\right)}\left(2\right),\cdots ,Q^{\left(0\right)}\left(k\right)\right)$ ； $Q^{\left(0\right)}$ 为 $Q^{\left(1\right)}$ 的一次累减生成序列，其中 $Q^{\left(0\right)}\left(j\right)=Q^{\left(1\right)}\left(j\right)-Q^{\left(1\right)}\left(j-1\right)$ ， $j=1,2,\cdots ,k$ 。

$z^{\left(1\right)}$ 为 $Q^{\left(1\right)}$ 的均值生成序列， $z^{\left(1\right)}=\left(z^{\left(1\right)}\left(1\right),z^{\left(1\right)}\left(2\right),\cdots ,z^{\left(1\right)}\left(k\right)\right)$ ，其中 $z^{\left(1\right)}\left(j\right)=0.5Q^{\left(1\right)}\left(j-1\right)+0.5Q^{\left(1\right)}\left(j\right)$ ，则称：

$Q^{\left(0\right)}\left(j\right)+A{z}^{\left(1\right)}\left(j\right)=B{\left(z^{\left(1\right)}\left(j\right)\right)}^m$ (7)

为GM(1,1)幂模型。

根据最小二乘法，GM(1,1)幂模型的参数可按下式求解：

$P=\left[\begin{array}{c}A\\ B\end{array}\right]=\frac{\left[\begin{array}{c}s\left(m+1\right)E-s\left(2m\right)D\\ s\left(2\right)E-s\left(m+1\right)D\end{array}\right]}{s\left(2\right)s\left(2m\right)-s^2\left(m+1\right)}$ (8)

其中： $s\left(v\right)={\displaystyle \underset{j=2}{\overset{k}{\sum }}{\left(z^{\left(1\right)}\left(j\right)\right)}^v}$ ( $v=2,2m,m+1$ )， $D={\displaystyle \underset{j=2}{\overset{k}{\sum }}{Q}^{\left(0\right)}\left(j\right)z^{\left(1\right)}\left(j\right)}$ ， $E={\displaystyle \underset{j=2}{\overset{k}{\sum }}{Q}^{\left(0\right)}\left(j\right){\left(z^{\left(1\right)}\left(j\right)\right)}^m}$ 。

GM(1,1)幂模型的白化方程为：

$\frac{\text{d}{Q}^{\left(1\right)}}{\text{d}t}+A{Q}^{\left(1\right)}=B{\left(Q^{\left(1\right)}\right)}^m$ (9)

根据式(6)和式(9)可以看出，Arps产量递减模型也是幂模型，是GM(1,1)幂模型在 $A=0$ 时的特例。

GM(1,1)幂模型白化方程的通解为：

$Q^{\left(1\right)}\left(t\right)={\left[\frac{B}{A}+C{\text{e}}^{A\left(m-1\right)t}\right]}^{\frac{1}{1-m}}$ (10)

式中：C为任意常数。取递减初始条件， $t=0$ 时 $Q=Q^{\left(1\right)}\left(1\right)$ 可以得到产量随时间变化公式：

$Q={\left\{\frac{B}{A}+\left[Q^{\left(1\right)}{\left(1\right)}^{\left(1-m\right)}-\frac{B}{A}\right]{\text{e}}^{A\left(m-1\right)t}\right\}}^{\frac{1}{1-m}}$ (11)

根据式(2)和式(10)可以得到：

$a=A-B\cdot Q^{m-1}$ (12)

将式(11)代入式(12)即可得到GM(1,1)幂模型的产量递减率随时间的变化公式：

$a=A-B\cdot {\left\{\frac{B}{A}+\left[Q^{\left(1\right)}{\left(1\right)}^{\left(1-m\right)}-\frac{B}{A}\right]{\text{e}}^{A\left(m-1\right)t}\right\}}^{-1}$ (13)

4. 模型的求解方法

不同油田产量的递减规律不同，表现在初始递减率 $a_{\text{i}}$ 和递减指数n不同，而又主要取决于n的变化情况。影响n的因素很多，如岩石性质、驱动方式、地质条件以及开采方式等，所以n变化范围很广，其选择和应用都比较麻烦。Arps产量递减模型采用标准曲线对比法求解 $a_{\text{i}}$ 和n，受主观影响大，误差大，尤其对于不规则序列，难以选择标准曲线。GM(1,1)幂模型可以满足多种形状序列的模拟，这主要取决于A、B和m的大小，但同样存在m求解难的问题。笔者通过构建最优化模型，利用智能算法求解m。

油田产量递减规律一般是随着时间推移，产量递减变慢，最后趋近于0。根据GM(1,1)幂模型的性质，进行产量递减预测时应有 $A>0$、 $m>1$ 。由式(7)，参数A、B可以看成m的函数，即 $P={\left[A,B\right]}^{\prime }=f\left(m\right)$ ，构建相对误差函数，建立以相对误差最小为目标的优化模型：

$\begin{array}{l}\min E\left(m\right)=\frac{1}{k}\left[{\displaystyle \underset{j=1}{\overset{k}{\sum }}\left|\frac{{\stackrel{⌢}{Q}}^{\left(1\right)}\left(j\right)-Q^{\left(1\right)}\left(j\right)}{Q^{\left(1\right)}\left(j\right)}\right|}\right]\times 100\%\\ \text{st}A>0,m>1\end{array}$ (14)

式中： ${\stackrel{⌢}{Q}}^{\left(1\right)}(j)$ ， $j=1,2,\cdots ,k$ 为预测值。

粒子群算法由于理论计算简单，收敛速度快而得到广泛应用。采用文献 [12] 提出的多种群多极值粒子群算法进行求解。

由于GM(1,1)幂模型和Arps产量递减模型形式不同，A、B和m只代表一个数值，没有实际意义，所以不能直接采用 $B=-\frac{a_{\text{i}}}{Q_{\text{i}}^n}$ 和 $m=n+1$ 计算Arps模型中的初始递减率 $a_{\text{i}}$ 和递减指数n。对于初始递减率，

正确的求解方法是根据式(12)，取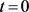进行求解。在GM(1,1)幂模型中没有递减指数的概念。

5. 实例分析

取文献 [1] 中某油田在生产后期的产量数据(表1)。文献 [1] 将产量变化曲线与标准图版对比，确定递减指数 $n=0.3$ 、初始递减率 $a_{\text{i}}=\text{0}\text{.05}$ ，从而得到产量和递减率随时间变化的关系分别为：

$Q=\frac{902.2}{{\left(1+0.015t\right)}^{1/0.3}}$

$a=\frac{0.05}{1+0.015t}$

采用GM(1,1)幂模型求解，得到 $A=0.00961$、 $B=0.00139$、 $m=1.65$ ，从而得到产量和递减率随时间变化的关系分别为：

$Q={\left\{-0.14464+0.15664{\text{e}}^{0.00284t}\right\}}^{-1.53846}$

$a=0.00961+0.00139\times {\left(-0.14464+0.15664{\text{e}}^{0.00284t}\right)}^{-1}$

预测结果见表1。

Table 1. The results of model prediction (data taken from reference [1] )

表1. 模型预测结果(数据来自文献 [1] )

*样本平均相对误差是根据式(14)计算得到，即 $\frac{1}{k}\left[{\displaystyle \underset{j=1}{\overset{k}{\sum }}\left|\frac{{\stackrel{⌢}{Q}}^{\left(1\right)}\left(j\right)-Q^{\left(1\right)}\left(j\right)}{Q^{\left(1\right)}\left(j\right)}\right|}\right]\times 100\%$ 。

从表1中的结果可以看出，相对Arps产量递减模型，GM(1,1)幂模型相对误差小，建模精度高。另外计算时发现在 $A<0$、 $m>1$ 和 $A>0$、 $0<m<1$ 两个区域，也可以达到很高的建模精度，但是根据长期预测，产量趋近于 ${\left(B/A\right)}^{\frac{1}{1-m}}$ ，不符合现场实际。主要原因是样本数据点少，贫信息，只能反映中、短期产量变化规律。对于长期预测，则需要更多的数据点。这也同时说明任何模型的建立，都必须以实际规律为基础。

6. 结论

1) GM(1,1)幂模型适合少样本、贫信息的不确定系统，能满足多种形状序列的建模。同时GM(1,1)幂模型与Arps产量递减模型在形式上存在共性，可以用来预测油气产量，建模精度高。

2) 在油田现场，受各种因素的影响，测试的数据带有一定的“噪声”，因此在建模过程中，不仅要追求建模精度，更要分析模型是否能反映实际生产规律。尤其是长期预测，要随时用最新的测试点更新模型。