1. 引言
近年来,为实现节能减排与生产工艺灵活调整要求,油田电网中变频器等非线性电力电子设备日益增加,且有随机接入系统的网电钻机、网电修井机等设备,导致油田电网谐波源数量和类型不断增加,谐波分布日趋复杂。谐波含量超标易造成补偿电容器无法投入甚至爆炸、谐波谐振以及保护误动作等问题,直接影响着油田供电系统的安全可靠运行 [1] 。所以,研究油田电网中谐波产生的机理、总结在油田生产设备中典型谐波源发生特性,分析谐波产生的影响是非常必要的。谐波在线监测系统可为分析和掌握油田电网谐波发射与传递规律,提供有效手段,但基于主站数据的系统状态评估方法等问题的研究较少,成为限制该系统应用与发展的瓶颈之一。
文献 [2] 选取节点注入功率和线路上的视在功率为量测量,基于关联矩阵,建立了状态量与量测量之间的数学模型,通过把节点注入分为非谐波源注入以及可疑谐波源注入两种类型减少了待求的状态量的数量。但由于对无功功率的理解没有形成统一的认识,因此该方法并没有说服力。文献 [3] 将谐波的状态估计视为一种优化问题,并且给出一种通过最下方差进行估计的算法,该文章将状态量选取为节点电压,量测量选取为支路电流和节点电压,通过最小二乘法对状态方程进行求解,但文章并没有考虑节点注入量测方程,因此其可观测范围受到影响。文献 [4] 提出了基于电力系统连续谐波的一种谐波状态估计方法,该文将母线分为两类,一类为非谐波源注入母线,一类为可能的谐波源注入母线。由于非谐波源注入母线的数量远多于可能的谐波源注入母线数量,因此该方法大大减少了未知的状态量。此外,在上述第二类可能的谐波源母线的基础上,将该类母线分为已有量测和没有量测两种情况,这种方法再一次减少了需求解的状态量的数量,结果表明这种方法是经济、高效且准确适用的,但其精确度难以保证。文献 [5] 和文献 [6] 提出了一种基于同步相量量测装置(PMU)的谐波状态估计方法,该文章选取状态量为节点电压,选取量测量为支路电流、节点电压和节点注入电流,通过加权最小二乘法对建立的谐波状态估计方程进行求解。并且依据量测量和状态量的选取方法,给出了谐波状态估计问题的统一数学模型和各种电路器件下相量量测方程。通过对量测节点编号的优化,提出了分层算法来降低稀疏矩阵的计算量,将状态估计问题从整个系统范围缩小到单母线系统范围,既降低了量测矩阵的维度,又降低了计算量,但其计算效率较低,运行较慢。
本文利用节点电压作为状态量,节点电压、支路电流和节点注入电流作为量测量,建立谐波状态估计数学模型。基于油田负荷运行监测系统数据,能够实时获取负荷运行信息,即某些支路虽然没有安装谐波量测装置,但能获得基波电流。利用各支路基波电流与节点注入基波电流之比等于各支路谐波电流与节点注入谐波电流之比,将量测方程由欠定变为正定,再利用最小二乘法求解。算例表明,该建模方法不仅能有效增加可观节点,而且能避免求解欠定方程带来的较大误差。
2. 配电网谐波状态估计方法
谐波状态估计与传统状态估计存在一些区别,不是简单的传统状态估计在谐波领域的拓展。尤其是同步相量量测技术的发展,使得谐波状态估计与传统状态估计的量测量类型发生了变化,从而使谐波状态估计在估计理论、数学模型及求解算法方面与传统状态估计有很大的区别。
传统状态估计选用节点的电压幅值、支路电流、节点注入有功、无功功率作为量测量,而谐波状态估计以节点电压、支路电流和节点注入电流为量测量,以节点电压为状态量。由于量测量的选取不同,谐波状态估计数学模型也需要重新建立 [5] [6] 。
2.1. 网络谐波模型的数学描述
根据网络中各节点、各元件之间的连接关系以及各元件的谐波模型,形成整个电网的节点谐波导纳矩阵。假设某连通的电力网络的节点数是n,支路数是b(包括接地支路)。对于频率为f的某次谐波,该网络的支路谐波导纳矩阵yf有如下形式 [7] :
(1)
其中,矩阵元素
的下标
表示支路编号。当
时,
表示第i条支路的自导纳,当
时,
表示第i条支路和第j条支路之间的互导纳。
对每条支路规定了正方向后,则其节-支关联矩阵A的阶次是
,A中的元素定义为:当节点i是支路k的发点,
;当节点i是支路k的收点,
;当节点i不是支路k的端点,
。
据此定义,A由图1所示:
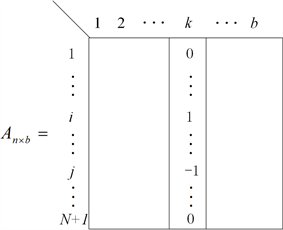
Figure 1. Node-to-branch incidence matrix A
图1. 节支关联矩阵A
矩阵A有b个列矢量,每一列与一条支路对应,表示该支路与哪两个节点相关联,所以每一个列只有1和-1两个非零元素,其余元素都为0,非零元素的正负表示支路的方向。上式只给出了第k条支路中非零元的情况。A中有
个行矢量,每一行与一个节点对应,表示该节点与哪些支路相关联,因此每行中非零元素的数目就等于该节点的度。
利用节点-支路关联矩阵和支路导纳矩阵求解节点导纳矩阵的公式为:
(2)
矩阵A反映了网络的拓扑约束,
反映了网络的支路特性约束,所以节点导纳矩阵集中了网络两种约束的全部信息。每次谐波都对应一个独立的支路导纳矩阵和节点导纳矩阵。
2.2. 谐波状态估计的数学模型
在一定的量测配置条件下,谐波状态估计利用网络谐波模型建立起各个谐波量测量和状态量之间的联系,即形成谐波状态估计的各个量测方程,量测方程的组合构成了谐波状态估计的数学模型。以谐波量测装置测量的谐波电压、谐波电流相量作为量测量,建立的谐波状态估计数学模型是线性的 [7] [8] [9] [10] ,因此,在电网络的拓扑结构、支路参数以及量测装置安装布局已知的条件下,谐波状态估计的数学模型为:
(3)
式(3)中:Z为m维量测量,通过量测装置直接读取;H为量测矩阵,表示谐波量测量和状态量之间的函数关系,与线路的拓扑结构、线路的参数以及量测装置的安装布点有关;
为量测误差;X为待解的n维状态量。
2.3. 谐波状态估计相量量测方程
谐波状态估计量测方程主要包括电压量测方程、节点注入量测方程、支路量测方程,这是谐波状态估计与传统状态估计数学模型的主要区别 [11] [12] [13] [14] 。
1) 电压量测方程
电压量测主要是指量测量为节点的电压向量。由于谐波状态估计选择节点谐波电压作为待求解的状态量,故电压量测方程也可称为自量测方程,其方程可表示为:
(4)
其中:
表示i节点h次谐波电压量测量;
表示i节点h次谐波电压状态量;
I表示适当维数的单位矩阵;
表示i节点h次谐波电压量测误差。
2) 节点注入电流量测方程
基于基尔霍夫电流定律(KCL),可知通过节点电流注入量测得到的量测值等于该节点各支路电流注入的相量之和,其方程可表示为:
(5)
其中:
表示i节点h次谐波注入电流量测量,中间节点的谐波注入电流值为0;
表示j节点h次谐波电压状态量;
表示节点导纳矩阵中对应节点i和j的分块导纳矩阵元素;
n表示网络节点总数。
3) 支路量测方程
流过支路的电流等于支路两端的电压与支路导纳的乘积,其方程可表示为:
(6)
其中:
为节点i到j之间支路的电流,
和
为节点i和节点j的节点电压,
对应节点i和j之间的导纳矩阵。考虑到油田线路属于配电网,故在等效线路模型时只考虑电阻和电抗。
4) 考虑基波电流比值的节点注入电流量测方程
基于油田负荷运行监测系统数据,能够实时获取负荷运行信息,即某些支路虽然没有安装谐波量测装置,但可以获得其基波电流。利用各支路基波电流与节点注入基波电流之比等于各支路谐波电流与节点注入谐波电流之比,得到考虑基波电流比值的节点注入电流量测方程:
(7)
其中:
表示i节点h次谐波注入电流量测量;
和
表示节点i到j和k之间支路的h次谐波电流;
和
表示节点i到j和k之间支路的基波电流;
表示节点i基波电流注入量。
2.4. 谐波状态估计求解方法
本文采用最小二乘法进行谐波状态估计。最小二乘法由数学家高斯于1795在研究星体运行轨道时提出的。由于最小二乘法要求系统的先验统计知识少,算法简单,计算量小,收敛性能好,因而被广泛应用于系统辨识、状态估计、自适应信号处理、自适应滤波、自校正控制等领域。它是以量测值和量测估计值之差的平方和最小为目标准则的估计方法 [9] 。
对于谐波状态估计数学模型:
(8)
式中:H为
参数矩阵,其元素为
;
为
估计误差矩阵。
利用最小二乘法建立目标函数:
(9)
对目标函J(X)求导,并让该值为0,即:
(10)
通过计算式(9),便可以求解出状态估计量X。
最小二乘解可以归为以下三类 [15] [16] [17] :
1) 矩阵H正定;有唯一解
(11)
2) 矩阵H超定;最小二乘误差解有唯一表示
(12)
其中
是Moore-Penrose广义伪逆。
3) 矩阵H欠定,最小2-范数
的唯一解:
(13)
谐波状态估计建模及求解过程如图2所示:
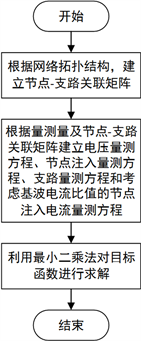
Figure 2. The flow chart of modeling and solving of Harmonic State Estimation
图2. 谐波状态估计建模及求解流程图
3. 算例分析
本算例基于胜利油田河口采油厂大一变电所某馈线及其所带负荷为研究对象,基于PSCAD软件建立了仿真模型。该馈线电压等级为6 kV,最大运行方式下短路电流3.64 kA,最小运行方式下短路电流2.77 kA。线路模型简化图如图3所示,其中:数字表示节点编号;支路“1_1”表示节点1与节点1_1之间支路,支路电流量测方向为节点1指向节点1_1,其他支路同理。算例以5次谐波为例,其他谐波类似。

Figure 3. Simplified schematic of Oilfield distribution network line
图3. 线路模型简化图
3.1. 监测装置的布点
共选择6处量测配置点,每处CT、PT安装路数如表1所示:

Table 1. Measuring equipment configuration
表1. 量测装置配置
3.2. 数据处理
各支路线路参数如表2所示:

Table 2. The parameter of field line
表2. 油田线路参数
各节点5次谐波电压量测量如表3所示:

Table 3. Measurement of node 5th harmonic voltage
表3. 节点5次谐波电压量测
各支路5次谐波电流量测如表4所示:

Table 4. Measurement of 5th branch harmonic current
表4. 支路5次谐波电流量测
3.3. 结果对比
通过运用最小二乘法对量测方程进行求解,结果如表5、表6所示:

Table 5. 5th harmonic voltage amplitude error comparison
表5. 5次谐波电压幅值误差对比

Table 6. 5th harmonic voltage phase error comparison
表6. 5次谐波电压相角误差对比
通过仿真值与计算值对比可以发现误差很小,通过对6个点进行谐波监测,可以实现对19个节点的谐波电压进行非常精确的监控。为了进一步扩大监测的范围,在线路模型中,选取了4个节点,即图2中a1~a4节点,通过求解欠定方程来求得这几个节点的谐波电压。求解过程如下:
首先在表4的基础上加上欠定方程需要的量测量,按照先后顺序为支路电流量测I5_2和I5_1,H矩阵也由19×19转换为21×23。结果如表7、表8所示:

Table 7. The 5th harmonic voltage ampitude of the node obtained by underdetermined equation
表7. 通过欠定方程求得节点电压幅值

Table 8. The 5th harmonic voltage phase of the node obtained by underdetermined equation
表8. 通过欠定方程求得节点电压相位
可见,此时通过欠定方程来进行求解存在的误差较大。可以根据基波的电气量来确定谐波的电气量的方法使误差减小。选取油田该馈线模型仿真结果中的基波电流比值作为谐波电流的比值,基波电流比值见表9:

Table 9. Fundamental wave current ratio
表9. 基波电流比值
根据表9,将欠定方程转变为正定方程,即在表4的基础上加上需要的量测量,按照先后顺序为支路电流量测0.57882倍的i5_2、0.4213倍的i5_2、0.643391倍的i5_1和0.356846倍的i5_1,此时不同于欠定情况,H矩阵由19×19转换为23×23。通过这种方法便可以把欠定方程修改成正定方程,计算结果如表10、表11:

Table 10. The 5th harmonic voltage ampitude of the node obtained by positive definite matrix
表10. 通过正定方程求得节点电压幅值

Table 11. The 5th harmonic voltage phase of the node obtained by positive definite matrix
表11. 通过正定方程求得节点电压相位
通过表10、表11可以看出,通过基波电流与谐波电流关系,将欠定方程修改为正定方程后,方程求解出的结果与仿真值误差明显减少。
4. 结论
为实现节能减排与生产工艺灵活调整要求,油田电网中变频器等非线性电力电子设备日益增加。且有随机接入系统的网电钻机、网电修井机等设备,导致油田电网谐波源数量和类型不断增加,谐波分布日趋复杂。谐波含量超标易造成补偿电容器无法投入甚至爆炸、谐波谐振以及保护误动作等问题,直接影响着油田供电系统的安全可靠运行。所以,有必要研究油田配电网中谐波产生的机理,掌握油田生产设备中典型谐波源发射特性。本文深入研究了谐波状态估计的数学模型,阐述了量测方程的建立方法和量测方程的两种求解算法,取得的主要成果如下:
1) 基于油田负荷运行监测系统数据,某些支路虽然没有安装谐波量测装置,但可以获取基波电流。利用各支路基波电流与节点注入基波电流之比等于各支路谐波电流与节点注入谐波电流之比,建立考虑基波电流比值的节点注入电流量测方程,将量测方程由欠定转为正定。
2) 对油田配电网某馈线进行建模,在6个节点安装谐波量测装置,进行谐波状态估计。通过最小二乘法得出的计算值和仿真出的结果误差较小,并且建立欠定方程求解了4个不精确的状态估计点,并在线路基波量测量基础上将欠定方程转化成了正定方程,减小了不精确点的误差。
算例表明,该建模方法不仅能有效增加可观节点,而且能避免求解欠定方程带来的较大误差。
基金项目
中石化重点科技攻关项目(317018-3)。