上海证券市场的CAPM实证检验

Empirical Test of CAPM in ShanghaiSecurities Market

摘要: 为了对CAPM模型在中国市场的适用性和有效性进行实证分析，从上证180指数中随机选取50支A股股票，并以2016年1月至2018年1月为研究时间段。在得出各支股票贝塔系数的基础上，进行风险和收益的横截面分析。实证结果表明，CAPM并不能完全适用于现阶段我国的A股市场。CAPM的局限性源于自身条件的限制和中国股市的不成熟。

Abstract: In order to empirically analyze the practicality and effectiveness of the CAPM model in the Chinese market, 50 A-shares from the SSE 180 Index are randomly selected, with the investigation period from January 2016 to January 2018. Based on calculation of the beta coefficient of each stock in advance, a cross-sectional analysis for both risks and benefits is performed. The empirical results show that CAPM cannot be fully applied to the current A-share market in China. The limitations of CAPM stem from the limitations of their own conditions and the immaturity of Chinese stock mar-ket.

1. 文献综述

自从1964年Sharpe (1964) [1] ，Lintner (1965) [2] 和Mossin (1966) [3] 提出资本资产定价模型(CAPM)以来，国外学者就该模型在以美国资本市场为代表的西方成熟资本市场上的适用性问题做了大量实证研究。Black，Jensen和Scholes (1972) [4] 以及Fama和MacBeth (1973) [5] 对1969年之前的数据进行检验，发现如CAPM模型所表述，平均股票收益与β系数之间确实存在正相关关系；Clare，Priestly和Thomas (1998) [6] 在英国股票市场进行检验，证明无法拒绝β系数与其截面平均收益呈正相关的假设。然而80年代以来，不一致的验证结果接踵而至。Reinganum和MarcR (1981) [7] 以及Lakonishok，Josef和Alan C.Shapiro (1986) [8] 均研究发现，在70年代以后的数据检验中，平均股票收益与β系数间不存在正相关关系。

我国证券市场起步较晚，二十世纪末才将CAPM模型引进并应用到各个投资决策和金融理论研究。杨朝军和邢靖(1998) [9] 对沪市股价的表现展开研究，通过对传统CAPM中平均收益和β系数关系进行实证研究以及对影响收益的其他因素做横截面检验得到以下研究结论：沪市的风险和收益关系与模型不相符，除系统风险外还存在其它决定收益的因素。陈浪南和屈文洲(2000) [10] 对CAPM进行实证检验，将股市划分为上升、下跌和横盘三种市场格局，在每种格局中分别检验β的解释力后得出：1) β系数对市场风险的度量有较为显著的作用，但β的均值以及β对收益率的解释程度在不同市场格局中存在显著差异；2) β系数与股票收益率之间的相关性较不稳定。翟羽(2015) [11] 以沪市前五批进行股权分置改革的60支股票为样本，对CAPM的适用情况进行实证研究。结果表明：在股权分置改革的背景下，CAPM在沪市具有一定适用性。姜婕(2016) [12] 从运输行业的28支股票中选取了15支代表股票，发现运输行业的β系数分析出的拟合效果不佳，故可以推测我国股市不是一个有效市场。朱光宇(2017) [13] 通过总结各方关于CAPM模型及其扩展在我国股市中的适用性实证检验，发现得到的结论众说纷纭，受到公认的、具有影响力的结果很少，目前尚未得出可以推动该领域发展的新理论，因此认为CAPM模型的研究在我国仍处于初级阶段。

综上所述，大多数实证研究表明CAPM模型在中国证券市场上的适用性较低，目前相关研究还处在初级阶段。然而，我国证券市场经过多年的发展，上市公司的规模和市场制度安排等也不断出现调整。因此，有必要通过新数据对CAPM的适用性和有效性进行重新检验，以观察影响我国证券市场的风险因素是否发生显著变化。

2. CAPM模型介绍和检验方法

20世纪60年代，Sharpe，Lintner和Mossin将马科维茨的均值方差理论延伸成为CAPM模型。CAPM认为投资者是基于均值-方差模型来进行投资的选择。在均值-方差模型中，证券市场存在一条有效前沿线，该线与一条从无风险利率出发的射线相切于某一点。马科维茨将这一切点定义为最佳有效资产组合，将这条线定义为资本市场线，即在所有组合中该点对应的有效投资组合最优。如果按照比例复制一个投资组合，使其与市场组合相同，各个投资者的区别在于其无风险资产和市场组合在其总资产的比例上。因此，市场组合是CAPM模型研究的基础。CAPM将资产收益与市场组合收益间的协方差同市场组合收益方差间的比值定义为该资产的系统风险，其方程表达式为：

$E\left(R_i\right)=R_f+\beta \left[E\left(R_m\right)-R_f\right]$ (1)

其中，E(R_i)是资产i的期望收益率；R_f指无风险利率；E(R_m)为市场组合的期望收益率，它是指所有风险资产组成的投资组合；β表示系统风险，是资产i与市场组合收益间的协方差，即：

$\beta =\mathrm{cov}\left(R_i,R_m\right)/{\sigma }^{²}{R}_m$ (2)

拟根据Fama和MacBeth (1973) [5] 提出的方法，将横截面回归方程与时间序列回归法相结合，进行CAPM实证检验。具体步骤如下：1) 划分时期。将样本数据分成三段进行检验，每个时间段包含若干周。2) 利用第一期的股价数据进行时间序列回归，计算出个股的β系数，记作β_i。3) 将第一期β_i按大小排序分组，构造投资组合，并在第二期对各组合再次进行时间序列回归得到组合的β系数，记作β_p。④将第二期组合的β_p作为自变量，利用第三期的组合周收益率做横截面回归检验CAPM模型。

3. 样本和数据

CAPM成立的前提是市场有效性且股票的价格应在时间序列上线性不相关。由于2015年6月至2016年1月处于股灾期间，此阶段样本不适合研究，因此选择的研究时间为2016年1月29日至2018年1月29日，每个时间段包含33周。研究对象为上证180指数当中的净收益率排名较优、分布在不同行业的50支股票。选择上证180指数作为市场指数。上证180指数作为一种价值加权指数，符合CAPM中市场组合构造的要求。在样本选取上将周收盘价作为观测值，无风险利率选取上海同业拆借利率。所有数据均来源于“同花顺数据中心”和“国泰安数据中心”。

3.1. 个股收益率

CAPM的实证研究大多选用月收益率，考虑到本次选择的时间段较短，采用月收益率将会导致样本量不足，故以下实证研究的观测值选用股票的周收益率。股票的周收益计算方法为：

$r_{i,t}=\left(P_{i,t}-P_{i,t-1}\right)/P_{i,t-1}$ (3)

其中，r_i,t表示第i支股票在第t的周收益率，P_i,t与P_i,t−1分别表示股票在第t周和第 $t-1$ 周的收盘价。

3.2. 市场收益率

采用上证180指数替代市场投资组合来计算市场收益率，计算公式如下：

$r_{m,t}=\left(W{I}_t-W{I}_{t-1}\right)/W{I}_{t-1}$ (4)

其中，r_m,t表示第t周的市场收益率， $W{I}_t$ 和 $W{I}_{t-1}$ 分别表示第t周和第 $t-1$ 周的指数。

3.3. 无风险利率

文献中通常以短期国债利率或银行同业拆借利率作为无风险利率，基于样本股票所处的市场环境，本次研究采用上海同业拆借利率代替无风险利率。

4. 实证分析

4.1. CAPM的时间序列检验

4.1.1. 计算个股 系数

首先根据第一期(前33周)数据计算出r_i,t和r_m,t，并通过R语言回归得出所有样本个股(共50支)的β系数即β_i。采用的单因素模型为：

$r_{i,t}={\alpha }_i+{\beta }_i{r}_{m,t}+{\epsilon }_i$ (5)

对式(5)取期望值，假设 $E\left({\epsilon }_{i,t}\right)=0$ ，于是有：

$E\left(r_{i,t}\right)={\alpha }_i+{\beta }_{i}E\left(r_{m,t}\right)$ (6)

由于篇幅限制，仅列出其中10支代表性股票的β回归结果，如表1所示。

Table 1. Time series regression results of the first period of sample stocks

表1. 第一期样本个股时间序列回归结果

4.1.2. 构造股票组合

由于单支股票存在较大的非系统性风险，易对收益与风险的关系产生偏差。为分散部分非系统性风险，先将第一期个股回归出的β_i依照大小关系每5个进行分组(共10组)，依照简单算术平均法算出组合超额收益r_p,t−r_f,t，根据以下公式(7)对组合再次做时间序列回归，得到组合β_p。回归模型为：

$r_{p,t}-r_{f,t}={\alpha }_p+{\beta }_p\left(r_{m,t}-r_{f,t}\right)+{\epsilon }_{i,t}$ (7)

对式(7)取期望值，假设 $E\left({\epsilon }_{i,t}\right)=0$ ，于是有：

$E\left(r_{p,t}-r_{f,t}\right)={\alpha }_i+{\beta }_{p}E\left(r_{m,t}-r_{f,t}\right)$ (8)

其中，r_p,t表示组合的收益率；r_m,t和ε_i,_t分别表示市场组合收益率和回归的残差。对第二期样本数据进行时间序列回归得到以下表2所示的结果：

Table 2. Time series regression results of the second period of stock portfolio

表2第二期股票组合时间序列回归结果

由表2可见，各组合的β_p值较为相近，大都在1左右，其显著性水平基本较小，这表明股票收益受证券市场收益的影响较明显。此外，60%的组合α_p均为显著，故拒绝零假设；同时，决定系数R²并没有随β_p值的增大而增大，这表明股票收益受除系统性风险外的其他因素的影响。

4.2. CAPM的横截面回归

根据第三期(最后33周)的数据，来计算第二期分组构成的10个组合在观测期内的周超额收益率的平均值：

$\overline{r_{p,t}-r_{f,t}}=\frac{1}{T}\underset{t=1}{\overset{33}{{\displaystyle \sum }}}\left(r_{p,t}-r_{f,t}\right)$ (9)

结合第二期的β_p，用以下模型：

$r_{p,t}-r_{f,t}={\gamma }_0+{\gamma }_1{\beta }_p+{\epsilon }_p$ (10)

进行横截面回归分析来检验回归系数 ${\gamma }_1$ 是否显著为零以及高系统性风险能否带来高期望回报率，即：

$E\left({\gamma }_1\right)=E(r_{m,t})-E\left(r_{f,t}\right)>0$ (11)

回归分析结果如表3及图1所示：

Table 3. Cross-sectional regression results of the third period of stock portfolio

表3. 第三期股票组合横截面回归结果

由表3可知，R²仅为0.4728，拟合度一般； ${\gamma }_1=0.0374$ 。从 ${\gamma }_1$ 的t检验值可以看出收益与系统性风险显著正相关，表明收益随风险的增大而增大，与CAPM模型较为相符；常数 ${\gamma }_0$ 显著不为零，表明存在系统性风险之外的其他因素。

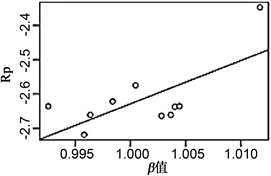
Figure 1. Regression scatter plot of the third period of stock portfolio βand the combined average weekly yield

图1. 第三期股票组合β值与组合平均周收益率的回归散点图

5. 结论

实证检验结果表明，收益与风险存在一定的正线性相关关系，即与CAPM模型的结论基本吻合，但在定价模型中系统风险并非唯一的决定因素，这样就不排除非系统风险也会对定价起到一定的作用。我国的证券市场起步较晚，股市规模较小，证券市场信息公开化程度较低，与发达国家的证券市场相比有较大差距。投资者的结构中个人投资者的数量占绝对优势，且投资者的投资观念不成熟，也是导致模型有所偏差的主要原因。经历过股灾洗礼后，不断增长的机构投资者逐渐成为我国证券市场的主体。随着多层次市场体系的建立和完善以及新股发行体制改革的深化，我国证券市场逐步走向成熟，证券投资中风险和收益的均衡关系将日益得到体现。