1. 引言
系统是指由一些基本部件(其中也可以包括人)组成的完成某种指定功能的整体 [1] 。根据部件之间的关系,可将系统分为串联系统,并联系统等。串(并)联系统类似物理学上的串(并)联电路。若有n个部件构成串联系统,当且仅当n个部件均正常工作时系统正常。若有n个部件构成并联系统,只要有一个部件正常工作,系统就正常工作。串联系统举例来说就如工厂生产流水线,只要其中一个环节出现问题,就无法完成生产流水线的根本目的。系统根据是否可修分为两类,是否可修则取决于技术经济问题。可修系统是指符合经济价值的系统,不可修系统则是不符合经济价值的系统。在现实生活中,电冰箱中制冷循环过程,机器人需要串接十四组马达的伺服驱动器,均是串联系统。显然串联系统在人们生活中无处不在。因此对于可修复串联系统的研究有极高的价值与意义。
本文针对部件不一定服从指数分布这一问题进行研究。可用于现实生活中计算不同型部件的串联系统的瞬时可用度与稳态可用度。目前对于三部件系统可靠性的研究,文献 [2] 针对修理工休假情况下的三部件系统进行讨论,通过补充变量法、拉普拉斯变换得出了休假情况下的可用度、可靠度。文献 [3] 在休假情况的基础上运用补充变量法对有优先修理权的三部件进行研究,得出系统的瞬态和稳态的可用度。文献 [4] 同样是对在休假情况下三部件串并联系统进行讨论,通过向量Markov过程方法、Laplace变换工具和补充变量法得出稳态下修理工处于休假状态的概率。文献 [5] 利用泛函分析方法对单部件可修系统的瞬时可用度,牢固可靠度进行分析。文献 [6] 则是在考虑修理工休假情况下的单部件可修系统。文献 [7] 则是针对两部件建立可靠性模型再通过泛函方法转换为抽象柯西问题。文献 [8] 则在基于文献 [7] 的结论证明了系统是稳定可解的。文献 [1] 对两个不同型部件串联可修系统进行研究,但并未对三个乃至n个不同型部件进行讨论。本文将基于以上论文对三个不同型部件串联非马尔科夫可修系统采用补充变量法,将其转化为广义马尔科夫系统来建立数学模型并求解。再推广到n部件讨论其一般性。
2. 系统假设与状态描述
2.1. 系统假设
三部件串联系统逻辑框图,如图1所示:
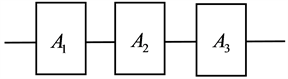
Figure 1. Logic block diagram of series system of three different types of components
图1. 三个不同型部件串联系统的逻辑框图
假设1在短时间内,不可能出现两个或两个以上部件同时失效的情况,设
为t时间内部件损坏个数,即对于充分小的
,有
[1] 。
假设2 部件
的失效时间服从参数为
的指数分布,设
为部件
在修复时间x内的修复可能。修复时间服从一般分布
,其中
。
假设3 部件失效后马上进行维修。
假设4部件之间相互独立。
2.2. 系统状态
用
表示系统状态,
状态0:
,无故障部件;
状态i:
,表示若t时刻部件
发生故障,
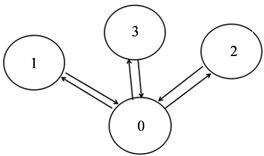
Figure 2. Three-component state transition diagram
图2. 三部件状态转移图
3. 模型建立
t为系统开始工作到目前状态的时间,显然
;记
表示
时,立即开始维修且持续维修时间为x,
。过程
是一个连续时间下的广义马尔科夫过程 [1] 。由于指数分布的无记忆性,可知t时刻前的过程与t时刻后的过程无关。令
表示t时刻系统因第i个部件发生故障而使系统驻留的时间为x的概率。记
为部件i的维修度,
为维修度的概率密度函数。
从图2中可以看出:当
内部件不发生故障时,
必然
。
有两种可能,第一种是
内系统一直处于正常工作状态未曾失效;第二种则是
内曾失效过但已经修复完成。因此:
从上试中可推出:
(1)
类似可得:
(2)
其中
,
.
系统初始条件:
(3)
边界条件:
(4)
当
时
,有
。
即三部件串联可维修系统的可靠性概率微分方程模型为:
(5)
4. 模型求解
利用初始条件和边界条件对模型(5)进行拉普拉斯变换,记
,得:
(6)
(7)
(8)
(9)
(10)
(11)
方程(7)是一个变量可分离方程,分离变量两边积分并带入(11)式,得
(12)
(13)
(14)
将(12),(13),(14)代入(6)可得
(15)
根据拉普拉斯公式可得
(16)
再将(16)代入(12)可得
(17)
与
也可类似得出。
即
(18)
系统的瞬时可用度为
,对它进行拉普拉斯变换得
,所以
根据拉普拉斯终值定理可知系统的稳态可用度为
,令
为修
理时间均值,通过洛必达法则可得出稳态可用度为:
5. 验证与推广
重复上述方法可知单部件可修系统可靠性数学模型为
其瞬时可用度与稳态可用度为
当
且
时,与参考文献 [6] 推论1所得出的稳态可用度结果相同。
双部件可修系统可靠性数学模型为
其瞬时可用度与稳态可用度为
当
且
时与参考文献 [8] 所得出的稳态可用度结果相同。
由上述公式可相应推广到n部件,可知其可靠性数学模型为
其瞬时可用度与稳态可用度为
当
且
时,其稳态可用度为
与参考文献 [9] 中n个相同部件串联可修系统的稳态可用度一致。
6. 小结
本文主要讨论在部件不服从指数分布情况下的三个不同型部件的串联可修系统,并推广至n部件。通过验证可知所求结果是较为真实有效的。因此该结论对相关方面的研究,具有较高的应用价值。并可用于解决实际生活中不同型部件系统的稳态可用度求解问题。
基金项目
南华大学研究生科学基金项目“可维修旁联系统可靠性分析与计算”(编号:2018KYY089)。