1. 引言
H-矩阵在计算数学,数学物理,控制论,统计学,弹性力学等众多领域中有着广泛应用。由于H-矩阵广泛的应用范围,其判定方法一直是人们关注的热点问题。因此,判别一个矩阵是否为H-矩阵及讨论其性质如何具有重大意义。由于近年来计算机的发展,国内外许多学者提出不少关于H-矩阵的迭代判定算法 [1] - [6] 。文献 [7] 以细化的思想通过对方阵行下标集及矩阵行和不同的递进式划分,得到了非奇异H-矩阵的若干判定定理和相应的迭代判定算法,增大对H-矩阵判定的范围,改进了文献 [8] [9] 中的结果。本文主要基于文 [7] 思路,针对文献 [10] 的判定结果做出改进得到一类迭代判定新算法,同时改进了文献 [10] 的判定定理范围和文献 [7] 的部分算法结果,最后用数值仿真结果说明了新算法判定的稳定性和高效性。
文 [7] 中给出了如下一个迭代判别算法。
算法A
输入:矩阵
输出:
,如果A是H-矩阵。
步骤1. 如果
或存在
使
,则“A不是非奇异H-矩阵”,停止;否则,
步骤2. 设
,
,
,
步骤3. 计算
,
步骤4. 如果
,则“A是非奇异H-矩阵”,停止;否则,
步骤5. 如果
,则“A不是非奇异H-矩阵”,停止;否则,
步骤6. 计算
,
,
,
,
,
,
,
步骤7. 令
。
步骤8. 如果
,则“A是H-矩阵”,停止;否则,
步骤9. 设
,其中
步骤10.
,返回步骤3。
2. 主要结果
主要基于文 [7] 的思想,本文通过对文 [10] 中H-矩阵判定结果的改进得到新的无参数迭代判别算法B,又适当选取参数得到更高效的带参数迭代判定算法C。
通过对算法中迭代阵因子及收敛条件的改进,下面给出较算法A判定范围更广的一个迭代算法。
设
为n阶复(实)矩阵的集合。
,记
,
,
,
,
,
,
,
,
,
,
,
.
,
.
2.1. 无参数算法
算法B
输入:矩阵
输出:
,如果A是H-矩阵。
步骤1. 如果
或存在
使
,则“A不是非奇异H-矩阵”,停止;否则,
步骤2. 设
,
,
,
步骤3. 计算
,
步骤4. 如果
,则“A是非奇异H-矩阵”,停止;否则,
步骤5. 如果
,则“A不是非奇异H-矩阵”,停止;否则,
步骤6. 计算
,
步骤7. 如果
,
且
或
时,存在
,使得
,则“A是非奇异H-矩阵”,停止;否则,
步骤8. 设
,其中
步骤9.
,返回步骤3。
注1:由上述符号可知,
,
。则
,
,有
.
所以,算法B具有比算法A更少的迭代次数。
在算法B的基础上,我们选取了适当的参数得到了下述算法C,它在一定程度上扩大了算法B的判定范围,修正了它判定结果的准确率,减少了运行迭代次数及时间。
2.2. 带参数算法
算法C
输入:矩阵
输出:
,如果A是H-矩阵。
步骤1. 如果
或存在
使
,则“A不是非奇异H-矩阵”,停止;否则,
步骤2. 设
,
,
,
步骤3. 计算
,
步骤4. 如果
,则“A是非奇异H-矩阵”,停止;否则,
步骤5. 如果
,则“A不是非奇异H-矩阵”,停止;否则,
步骤6. 计算
,
步骤7. 如果
,
且
或
时,存在
,使得
,则“A是非奇H-矩阵”,停止;否则,
步骤8. 设
,其中
其中
。
步骤9.
,返回步骤3。
3. 算法收敛性分析
下面通过定理1给出算法B作为H-矩阵迭代判定的收敛性分析。
定理1. 矩阵
是H-矩阵当且仅当算法B经有限次迭代生成一个严格对角占优矩阵而停止。
证明 假设矩阵A是非负矩阵。用
和
表示算法A的迭代过程中前一次和当前次迭代矩阵,其中m是某一迭代次数。
充分性:假设算法B经过m次迭代停止生成一个严格对角占优矩阵,则得到一个严格对角占优矩阵
,其中
是正对角矩阵。显然此时A是H-矩阵。
必要性:令A是H-矩阵。利用反证法,假设算法B经过有限次迭代不停止。由算法B可知
,其中
是对角元小于1的正对角矩阵,则
,
即无穷矩阵序列
单调递减且有界,因此有
,
其中
,
是正对角矩阵。
接下来,要证明
.
再次利用反证法,假设
,则
,
,
且存在某一
及常量
使得
,
,
,
令
。
由算法B,有
,
,
.
因此
,
令
,则
,产生矛盾。故
.
这说明矩阵B不是H-矩阵。另一方面,由于A是不可约H-矩阵,则存在一个正对角矩阵E使得
是严格对角占优的。易知,
仍是正对角矩阵,从而可得矩阵B是H-矩阵,产生矛盾。故算法B经有限次迭代停止。
算法A是利用对矩阵下标集的迭代细分来划分其占优与非占优指标集,一定程度上增大了它判定的范围,但迭代过程相对繁琐导致运行迭代次数与时间相对增加。算法B是构造新的迭代因子得到的新算法,由更小的对角阵迭代因子将使得算法运行的迭代次数和时间相比算法A需要的更少,且乘积因子对不等式的放缩使得判定范围比前者更广。在算法B基础上添加参数得到算法C,相比前两个算法运行的迭代次数和时间更小、判定范围更广,且在一定程度上修正了前两个算法判定结果的正确率,后面的数值仿真实验结果也说明了这一点。
4. 数值仿真
本文通过数值仿真实验测试比较了3个算法程序的性能,测试中随机选取近年来H-矩阵迭代算法相关论文的18个真实样本。综合实例的适用度,在带参数的算法C中q的取值为q = 4。实验机器选用联想台式机,具体配置:(Inter(R)Core(TM)i5-4590 CPU@3.30GHz,双核处理器8.00G内存64位windows操作系统),用Matlab R2013a语言编程实现。
根据算法A、B、C对不同样本运行产生的迭代次数,我们得到了数值仿真结果如图1所示(横坐标为样本编号,纵坐标为迭代次数)。由图1可以看出三个算法中算法C产生的迭代次数相对是最小的。针对算法有无参数对算法B、C产生的迭代次数作出对比可以看出,算法C相较算法B产生的迭代次数相对较少。综合图像来看,算法A的迭代次数明显高于后两个算法,且对某些样本实例的判定次数偏高,出错率也是三者中最高。算法B、C产生的次数相对较少且稳定在低次数段,两者的出错率相比算法C更低。
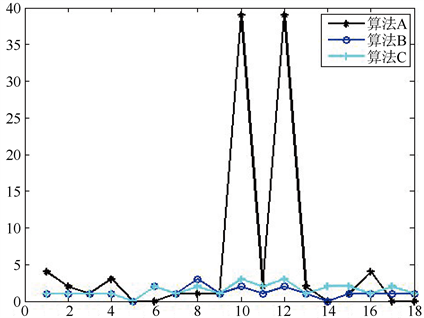
Figure 1. Curve: system result of iterative Algorithm
图1. 算法迭代结果曲线

Table 1. Resulting data of Algorithm runtime
表1. 算法运行时间结果数据
根据以上3个算法对不同实例产生的运行时间,得到运行时间表1。对算法产生的运行时间,运用SPSS软件对其做单因素方差分析。由其中的一项输出结果表2,单因素方差分析表,可以看出方差检验统计量F = 31.120,相应的sig值等于0.000,小于显著性0.05,因此我们认为不同算法的运行时间有显著性差异。再根据表1的结果可以说明算法A运行的时间与其他两个算法有较大差异,算法A花费的时间最多。

Table 2. One-way analysis of variance (ANOVA)
表2. 单因素方差分析表
为了检验不同的算法对不同实例结果判定的正确性,得到相应算法的正确率表3。

Table 3. Table of Algorithmic correct rate
表3. 算法正确率表
考虑到算法运行产生的迭代次数、判定结果的正确率和时间对算法的重要性不同,运用层次分析法做出了比较矩阵,并在matlab上实现依次得到它们的权重系数为0.5390、0.2973、0.1638。根据上述结果,对本文中3个算法做出算法综合评估表4。

Table 4. Data of Algorithmic comprehensive performance
表4. 算法综合性能数据
注2:本文在实例判定结果上,将运行判定结果出错或者无限循环结果在迭代次数中记迭代次数为0次,在正确率判定中判定为结果错误。在运行迭代次数及运行时间的数据处理中,将出错结果的迭代次数和时间分别用其它实例的平均迭代次数和时间替代,以减少对其它数据的影响。
5. 结论
从上述数值仿真分析结果来看,算法B的综合性能值是最低的,即算法B从迭代产生的次数、时间和正确率综合来看相较其他算法是最好的。从算法的判定式语句来看(即步骤7或者步骤8),算法C对H-矩阵的判定范围较算法B更广,且这两个算法判定H-矩阵的范围亦优于算法A的判定范围。其次,综合性能值较低的带参数算法C,它对实例判定结果的准确度最高,在对准确度的需求最高的情况下,它无疑是最好的选择。总体来看,得到的两个新算法不论在迭代产生的次数、时间还是正确率方面,相较文 [7] 的算法A都是有显著优势的。
致谢
感谢王海波等同学在算法数值仿真实验中所做的工作。
基金项目
国家自然科学基金(11461027)和湖南省教育厅科研基金(16A173)。
NOTES
*通讯作者。