1. 引言
系统动力学(system dynamics)起源于美国,“系统动力学是系统科学理论和计算机仿真紧密结合,研究系统反馈结构和行为的一门科学。”系统动力学由麻省理工学院教授Jay W. Forrester始创于1956年,经过随后的发展成为一门认识系统问题和解决系统问题探索系统行为的独立学科。系统动力学在早期主要研究工业系统因此被称为“工业动力学”,从系统的角度解决问题,将所考虑的问题放在一个系统中,确定系统的边界再逐步确定系统的结构,其主要思想是“系统的结构决定系统的行为”。系统动力学是系统科学理论和计算机仿真紧密结合,研究反馈结构和行为的一门学科。系统动力学的基础理论是系统论和反馈控制理论,系统动力学的主要目的是研究一个系统的结构并从整体角度通过结构分析研究系统的动态行为即研究系统行为随着时间变化的变化。系统动力学的目的不是寻求最优解,而是寻求改善系统行为的可能途径。它是将现有的信息通过系统结构联系起来,借助计算机软件和仿真语言进行动态模拟,对系统未来行为的仿真和描述。同时,系统动力学是在总结运筹学的基础上,为适应现代社会系统的管理需要而发展起来的。它不是依据抽象的假设,而是以现实世界的存在为前提,不追求“最佳解”,而是从整体出发寻求改善系统行为的机会和途径。从技巧上说,它不是依据数学逻辑的推演而获得答案,而是依据对系统的实际观测信息建立动态的仿真模型,并通过计算机试验来获得对系统未来行为的描述。简单而言,“系统动力学是研究社会系统动态行为的计算机仿真方法”。具体而言,系统动力学包括如下几点。① 系统动力学将生命系统和非生命系统都作为信息反馈系统来研究,并且认为,在每个系统之中都存在着信息反馈机制,而这恰恰是控制论的重要观点,所以,系统动力学是以控制论为理论基础的;② 系统动力学把研究对象划分为若干子系统,并且建立起各个子系统之间的因果关系网络,立足于整体以及整体之间的关系研究,以整体观替代传统的元素观;③ 系统动力学的研究方法是建立计算机仿真模型——流图和构造方程式,实行计算机仿真试验,验证模型的有效性,为战略与决策的制定提供依据。
系统动力学于20世纪70年代末引入中国,国内系统动力学的研究领域广泛涉及生态环保、社会保障、物流与供应链、产业研究、城市交通、可持续发展、商品价格等。国内学者主要集中于系统动力学的应用研究,通过分析系统结构,确定系统目的,构建因果回路图和库流图对系统中关键参数的量化分析,在此基础上,进行实例分析 [1] [2] [3] [4] [5] 。
在对自然资源的合理利用中,系统动力学提供了一个有效的管理工具,基于实验研究的基础上,综合主要影响因素,给出比较优的可能结果。系统动力学目前广泛应用于生态 [6]、风险评价 [7]、经济效益 [8]、港口发展 [9]、项目管理 [10]、战略管理 [11] 等方面,而系统动力学在水资源管理方面主要研究水环境质量、水资源承载力、水资源开发利用、水资源规划等 [12] [13] [14] 。
2. 系统动力学建模流程
系统动力学对问题的理解,是基于系统行为与内在机制间的相互紧密的依赖关系,并且透过数学模型的建立与操作的过程而获得的,逐步发掘出产生变化形态的因、果关系,系统动力学称之为结构。所谓结构是指一组环环相扣的行动或决策规则所构成的网络,例如指导组织成员每日行动与决策的一组相互关联的准则、惯例或政策,这一组结构决定了组织行为的特性。构成系统动力学模式结构的主要元件包含下列几项,“流”(flow)、“积量”(level)、“率量”(rate)、“辅助变量”(auxiliary) (Forrester, 1961)。系统动力学将组织中的运作,以六种流来加以表示,包括订单(order)流、人员(people)流、资金(money)流、设备(equipment)流、物料(material)流与信息(information)流,这六种流归纳了组织运作所包含的基本结构。积量表示真实世界中,可随时间递移而累积或减少的事物,其中包含可见的,如存货水平、人员数;与不可见的,如认知负荷的水平或压力等,它代表了某一时点,环境变量的状态,是模式中资讯的来源;率量表示某一个积量,在单位时间内量的变化速率,它可以是单纯地表示增加、减少或是净增加率,是资讯处理与转换成行动的地方;辅助变量在模式中有三种涵意,资讯处理的中间过程、参数值、模式的输入测试函数。其中,前两种涵意都可视为率量变量的一部分。 系统动力学的建模基本单位-资讯回馈环路结构的基本组成是资讯回馈环路(information feedback loops)。环路是由现况、目标以及现况(积量)与目标间差距所产生的调节行动(率量)所构成的,环路行为的特性在消弭目标与现况间的差距,例如存货的调节环路。除了目标追寻的负环外,还有一种具有自我增强(self-reinforced)的正回馈环路,即因果彼此相互增强的影响关系,系统的行为则是环路间彼此力量消长的过程。但除此之外结构还须包括时间滞延(time delay)的过程,如组织中不论是实体的过程例如生产、运输、传递等,或是无形的过程例如决策过程,以及认知的过程等都存在着或长或短的时间延迟。系统动力学的建模过程,主要就是透过观察系统内六种流的交互运作过程,讨论不同流里,其积量的变化与影响积量的各种率量行为。
系统动力学的主要问题在于分析系统的结构,确定系统结构首先需要根据所要研究的问题确定系统边界,分析系统内部各要素之间的因果关系并画出因果图,之后根据各要素之间的因果关系将系统划分为几个子系统,用流程图将各个子系统连接起来,确定了系统的整体结构之后,设置各要素的变量属性,并输入变量之间的方程式,模型检验无错误后进行仿真,系统动力学模型的构建主要包含以下几个步骤:
1) 确定系统边界
建立系统动力学模型的首先明确所要研究的问题,根据问题确定系统的边界,确定系统的边界就是考虑系统中应包含哪些因素,去除那些不需要考虑的因素。与所研究问题有重要关系的因素应纳入系统,而与研究问题关联弱的因素则不予考虑。系统边界决定了系统的复杂程度和系统的大小,系统边界直接关系到模型的仿真结果,如果系统边界确定的不合理,得出的结果可能无法解决问题,可能引发错误的决策。
2) 画出因果关系图
在确定系统边界之后,将系统内部互为因果的因素用带箭头的曲线连接起来即因果链,在因果链附近用正号或负号标示,表示因与果是同向变动或反向变动。
① 因果链
图1中的左图是系统动力学模型中的最小构成,表示两要素之间的因果反馈,GDP的增加使得人均GDP增加,同时,人均GDP会随着GDP的减少而相应减少,说明GDP的变化(因)带来了人均GDP的变化(果),“+”则表示两者同向变动,因果之间呈现正反馈作用即正因果链。而右图显示利率与投资支出之间的负反馈即负因果链,利率降低促进投资,投资支出增加,相反如果利率上升则抑制投资,投资支出则减少。
② 因果回路
因果回路又称为反馈环(causal feedback loop)由两个及两个以上依次相互作用的因果链构成的封闭回路。因果回路同因果链一样也有正负之分,在正因果回路中,一个变量的变化最终使自身同方向变化的趋势增强,而在负因果回路中,一个变量的变化最终使自身同方向变化的趋势减弱。因果回路的极性由回路中负因果链数目的奇偶决定。如果一条回路中含有奇数个负因果链则回路的极性为负,如果回路中的负因果链为偶数个则极性为正。如图2:
在因果回路中,各要素互为因果相互影响,左图中含有两条负因果链则因果回路为正,右图中含有一条负因果链则因果回路为负。
3) 确定子系统
根据系统边界内各要素之间的因果关系,将系统划分为几个子系统,分别研究各个子系统的结构和反馈机制,最终通过流程图将各个系统连接成一个整体。
4) 画出系统流图
系统流图是依据因果关系图,通过明确各变量的属性,用系统动力学特有的符号连接各个变量。流图中主要包含水平变量、辅助变量、速率变量、常数。
① 水平变量(Level)
水平变量用来表示系统的累积效应,又称为状态变量,反映物质、信息、能量随时间变化的积累,是对物质、信息、能量存储。
② 辅助变量(Auxiliary)
辅助变量帮助描述信息反馈的变量,位于水平变量与速率变量之间。
③ 速率变量(Rate)
速率变量又称为流率变量,用来表示水平变量的变化快慢。
④ 常数(Constant)
常数(常量)是在一个计算过程中不随时间变化的量。
5) 输入变量方程
将反映各变量之间的关系用数学方程表示出来,输入系统动力学模型中。
6) 模型参数设计
根据模型中的变量方程,明确模型中的参数,系统动力学模型中一般有常数类、转换系数、状态变量的初始值等几类参数,通过参数估计方法对参数进行合理设计。
7) 模型仿真
在检验模型没有错误之后,包括对模型单位以及变量方程等的检验,运用系统动力学专门的软件(如STELLA、VENSIM等)进行模拟。
8) 模型检验
模型初步建成后,在仿真前需对模型进行初步检验即单位检验和模型检验,及时发现模型中的错误,以便模型顺利运行。
9) 模型仿真调试及最后决策方案确定
在模型检验无错误之后,进行模拟,对模拟的结果分析,然后设定政策方案,进行方案的比较和决策。
3. 污水初始排放权定价模型构建
3.1. 模型子系统的确定
本文选取化学需氧量为指标,所以污水初始排放权价格等于COD平均处理成本。运用系统动力学方法分析排放权价格,确定排放权价格系统的边界,废水产生是由于生活用水和生产用水,生活用水由人均用水量和人口数量决定,生产用水由每元GDP用水量和GDP决定,所以系统中应该包含水资源子系统、人口子系统、经济子系统,由于废水排放造成环境污染,降低了社会效益,为了治理和控制水环境污染须投入人力、物力、财力,故系统中也包含社会子系统,因此系统分为水资源子系统、人口子系统、经济子系统、社会子系统。
3.1.1. 水资源子系统
水资源子系统是整个系统的核心部分,由用水需求引发排水需求,用水量主要包括居民生活用水以及生产过程用水量两部分,其中生活用水量由人均生活用水量决定,生产用水量由GDP增加值决定。大部分水经使用后最终以废水的形式排放,生活用水经使用后80%以上以废水形式排放通过污水排放系数将用水总量与污水排放总量联系起来,
水资源子系统中系统动力学主要变量方程有:
用水总量 = 生产用水量 + 生活用水量
生产用水量 = GDP * 每元GDP用水量
生活用水量 = 人均生活用水量 * 总人口数量
污水排放总量 = 污水排放系数 * 用水总量
污水处理总量 = 污水处理率 * 污水排放总量
COD排放总量 = 每吨污水COD含量 * 污水排放总量
水资源子系统流图如图3:

Figure 3. The flow chart of water resources subsystem
图3. 水资源子系统流程图
3.1.2. 人口子系统
人口子系统是系统中重要组成部分,人口数量变动的影响生活需水量的变化,从而影响污水排放量,引起社会平均COD处理成本变动,即影响污水初始排放权价格。人口子系统包括总人口数量、人口增长值、人口增长率,总人口数量为状态变量表示人口的累积,系统中主要变量方程如下:
总人口数量 = 总人口数量初始值 + 人口增长值
人口增长值 = 总人口数量初始值 * 人口增长率
人口子系统流图如图4:

Figure 4. The flow chart of population subsystem
图4. 人口子系统流程图
3.1.3. 经济子系统
生产活动促进经济增长,同时需要消耗水资源,并向环境排放生产过程中产生的含有化学物质的污水。经济子系统中包含的要素有GDP(国内生产总值)、GDP增加值、GDP增长率,其中GDP为状态变量。其系统动力学方程为:
GDP = GDP + GDP增加值
GDP增加值 = GDP * GDP增长率
经济子系统流图如图5:
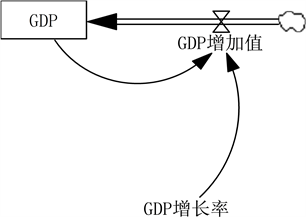
Figure 5. The flow chart of economic subsystem
图5. 经济子系统流程图
3.1.4. 社会子系统
社会子系统主要包括一些为了提高社会效益而采取的措施,为了改善治理水污染投入的财力(固定资产投资等)、物力(排水管道建设等)、人力(污水处理人员、管网养护人员)等。变量方程有:
固定资产 = 固定资产+固定资产增加额
固定资产增加额 = 固定资产 * 固定资产增加率
固定资产折旧额 = 固定资产 * 固定资产折旧率
管网运行人员 = 平均每人养护管网长度 * 排水管道长度
工资总额 = 污水处理人员工资 + 管网人员工资
排水管道长度 = 排水管道长度 + 排水管道长度增加值
排水管道长度增加值 = 排水管道长度增加率 * 排水管道长度
污水处理人员 = 平均人员配备比例 * 污水处理总量
污水处理人员工资 = 污水处理人员 * 职工平均工资
管网人员工资 = 管网运行人员 * 职工平均工资
社会子系统流图如图6。
3.2. 系统动力学流程图绘制
系统动力学流程图见图7。
3.3. 模型变量说明
模型中共包含43个变量,其中状态变量有5个:固定资产、职工平均工资、排水管道长度、总人口数量、GDP,以及反映状态变量变化速度的5个速率变量,21个辅助变量,12个常量(见表1)。
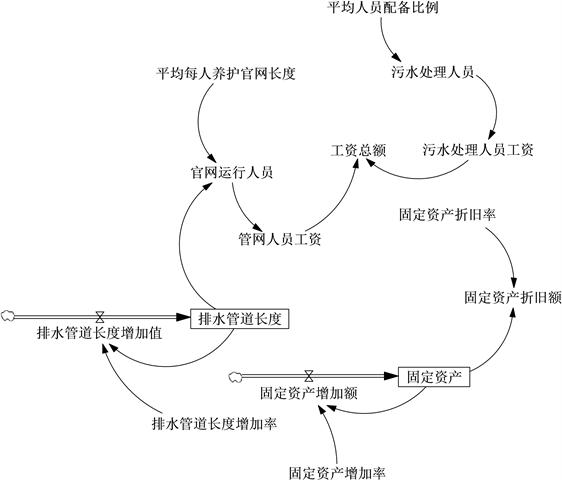
Figure 6. The flow chart of social subsystem
图6. 社会子系统流程图

Figure 7. The flow chart of system dynamics
图7. 系统动力学流程图
3.4. 系统动力学变量方程
根据污水初始排放权定价系统动力学混合图建立变量方程,变量方程用来确定变量间的数学关系,初步确定了27个变量方程:
1) COD平均处理成本 = COD年运行总成本/COD年处理总量
2) COD年运行总成本 = 固定资产折旧额 + 工资总额 + 年运行费用 + 耗电费用
3) 固定资产折旧额 = 固定资产折旧率 * 固定资产
4) 固定资产 = 固定资产 + 固定资产增加额
5) 固定资产增加额 = 固定资产增加率 * 固定资产
6) 工资总额 = 污水处理人员工资 + 管网人员工资
7) 污水处理人员工资 = 污水处理人员 * 职工平均工资
8) 污水处理人员 = 平均人员配备比例 * 污水处理总量
9) 管网人员工资 = 管网运行人员 * 职工平均工资
10) 管网运行人员 = 平均每人养护管网长度 * 排水管道长度
11) 排水管道长度 = 排水管道长度 + 排水管道长度增加值
12) 排水管道长度增加值 = 排水管道长度增长率 * 排水管道长度
13) 职工平均工资 = 职工平均工资 + 职工平均工资增加
14) 职工平均工资增加值 = 平均工资增长率 * 职工平均工资
15) 年运行费用 = 平均每吨运行费用 * COD年处理总量
16) 耗电费用 = COD年处理总量 * COD电单耗 * 平均用电价格
17) COD年处理总量 = COD去除率 * COD排放总量
18) COD排放总量 = 每吨污水COD含量 * 污水排放总量
19) 用水总量 = 生产用水量 + 生活用水量
20) 生活用水量 = 人均生活用水量 * 总人口数量
21) 总人口数量 = 总人口数量 + 人口增长值
22) 人口增长值 = 人口增长率 * 总人口数量
23) 污水处理总量 = 污水处理率 * 污水排放总量
24) 污水排放总量 = 污水排放系数 * 用水总量
25) 生产用水量 = 每元GDP用水量 * GDP
26) GDP = GDP + GDP增加值
27) GDP增加值 = GDP增长率 * GDP
3.5. 模型参数设计
模型的参数由模型的变量方程确定,根据以上变量方程可知模型中的参数有固定资产折旧率、固定资产增加率、平均人员配备比例、平均每人养护管网长度、排水管道长度增长率、平均每吨运行费用、平均工资增长率、每吨污水COD含量、COD电单耗、平均用电价格、COD去除率、人均生活用水量、人口增长率、污水处理率、污水排放系数、每元GDP用水量、GDP增长率等参数。模型参数的合理设计不仅决定模型准确程度还会影响最终决策方案的选取,所以模型参数设计须符合实际。模型参数的估计主要有以下几种方法:
1) 通过现有的数据整理所得
2) 对模型中变量方程分析获得参数值
3) 根据已有的相关系统知识对参数合理估计
4) 根据实际要求在上限和下限之间合理选择参数值
5) 通过模型参考行为特性分析估计参数
4. 结论
综上,本文主要进行了污水初始排放权定价模型的构建,首先确定了水资源子系统、社会子系统、经济子系统、人口子系统四个子系统,在分析各子系统之间的关联关系基础上画出系统动力学流程图,对模型中各变量的属性进行了说明,然后根据各变量之间的相互关系初步确定了27个变量方程,最后对模型中的17个参数进行设计,以此构建了污水初始排放权定价模型。预期为污水初始排放权的系统建模进行理论扩充,同时,为环保管理当局进行相关决策提供依据。
基金项目
2017年辽宁省科技厅自然科学基金项目;项目号:20170540439;项目名称:基于中微观的污染控制模型体系构建。
NOTES
*通讯作者。