1. 引言
许多复杂系统的演变过程都存在着临界点,比如种群生物数量系统、金融市场、气候系统、癫痫发作等系统中都存在着在某个很短的时间段内系统从一个稳定状态迅速转变到另一个稳定状态的现象。在临界点时期,复杂系统的鲁棒性急剧降低,状态转移风险大幅升高 [1] 。关于复杂疾病的临界点,相关的研究已经取得了许多有效的成果,比如最近有国内学者提出了利用动态网络生物标志物进行复杂疾病临界点探测的方法 [2] [3] [4] 。一般而言,可以将复杂疾病(比如肝癌、糖尿病、癫痫等)的发展过程划分为三个阶段,分别是健康阶段、临界阶段、疾病阶段,其中临界阶段持续的时间相较于其他阶段而言非常短暂。处于健康阶段的系统比较稳定,不易受到外界环境的扰动而改变,具有较强的恢复力和鲁棒性。而临界阶段的系统恢复力和鲁棒性均很弱,状态很不稳定,经过及时治疗,系统可以从临界阶段恢复到健康阶段,一旦系统进入了疾病阶段,则系统便处于了另一个较稳定状态,即疾病已经发展到重症阶段,再给予多大强度的治疗,系统也难以从疾病阶段恢复到健康阶段。
预测复杂疾病进展过程中的临界点具有非常重要的实际意义,但这项工作却是非常困难的。前人提出的单纯利用基因表达浓度的变化得到相关的不一致性指标的方法是静态的方法,不适用于探测复杂疾病的临界点。而利用传统的临界慢化法则需要病人提供大量的时序列样本数据,现实情况下难以在短时间内获取符合要求的疾病数据,所以利用生物网络对复杂疾病进行早期诊断是大势所趋。最近有学者提出了利用单个样本检测复杂疾病临界点的方法 [5] ,本文则基于利用单个样本与已知样本结合局部网络 [6] [7] [8] [9] [10] 以及熵的概念 [11] [12] [13] [14] 开发出了一个新的探测复杂疾病临界点的算法。本文首先利用希尔方程建立具有11个结点的复杂疾病生物仿真网络,并将我们的算法应用于仿真网络生成的数据,算法成功探测出了仿真数据的临界点。然后对NCBI生物网站上的小鼠肺光气实验(GSE2565)这个真实的高通量时序列数据应用本文的算法进行研究发现,该疾病即将恶化的预警信号出现的时间点与实验观察的结果吻合。
2. 方法
2.1. 单样本网络熵的推导
由于生理现象的复杂性,影响生理状态的因素非常多,目前尚无法用一个微分方程来描述。对于复杂疾病的临界点这个特殊时期,疾病的发展依赖于某几个主导因素,于是通过研究低维的动力系统微分方程来代换高维而复杂的疾病生理系统 [2] [3] [4] 。
对于一个复杂疾病临界点时的系统,可通过建模成为离散的动力系统:
. (1)
在系统(1)中的
代表固定t时刻下n维基因表达浓度的状态变量,参数向量
代表生理系统的驱动因子,比如基因拷贝数变异、DNA甲基化等。
系统(1)需要满足一些条件:1) 存在不动点
满足
;2) 存在
使得雅可比矩阵
, (2)
有一个或一对特征值的模等于1;3) 当
时,系统(1)的特征根的模不总等于1。这三个条件意味着当P达到阈值
时该系统在
处经历了一个相变或一个余维数一的分岔。
在系统(1)的
附近,当P到达
前,按假设系统应该会留在一个稳定的不动点
上,因此所有的特征值的模是在(0,1)之间的。在系统处于临界点时的参数值
称为分岔点值或临界跃迁值。
现在考虑系统(1)的线性化近似方程,具体而言,通过引入新的变量
和
一个可逆的转换矩阵S,即
. (3)
结合系统(1)有
,(4)
(4)式中
是均值为零的微小高斯噪声,
的标准偏差为
,
是关于参数P的对角矩阵。
根据假设,对角化矩阵
的每个
的模均在0和1之间。不失一般性,在
的特征值中,假设模最大的一个为
,当参数转换
发生时,
是第一个到达1的。特征值
表征了系统围绕不动点改变的速率,
被称为占主导地位的特征值。系统远离临界点时的状态对应于
,而系统趋近临界点时的状态对应于
。设Y中与
相关的变量为
,又根据方差与均值的性质得到
的方差为
, (5)
当主导特征值
时,从(5)式中,可以得到变量
的标准偏差急剧增加的结论。因此,当系统处于远离临界点的状态时,
远小于1并且没有大的变化,
和
之间的分布也没有明显的变化。然而,当该系统处于趋近临界点时的状态,即
接近1时,
和
这两者的分布便有差异。
对于以第i个结点为中心的局部网络,假设总共有m个一阶邻居
,现令随机变量
代表局部网络的状态,局部网络中结点的值为0或1,则
总共取值个数为
,设
代表t时刻第u个局部网络并且状态为v的概率,则第i个局部网络的熵为
, (6)
整体网络熵为
. (7)
系统远离临界点时,假设局部网络中某个结点
为显著改变状态,即值取1的概率为
, (8)
其中
,
为t时刻单样本第
个基因的表达浓度值,
为t时刻已知样本第
个基因的表达浓度值,所以结点
为不显著改变状态即值取0的概率为
, (9)
因为正常状态下基因表达稳定,所以
,即
. (10)
令第i个局部网络的状态
,则有
, (11)
而
,所以局部网络i处于
以外的其他状态的概率是趋于0的,
故在正常状态有
. (12)
而系统趋近于临界点时,对于第
个结点,有
,其中
为第
个基因的表达浓度值,而
,故有
, (13)
也即说明
的离散程度非常高,对于第i个局部网络,有
, (14)
和
. (15)
针对(14)和(15)二式引入拉格朗日乘子
,得到
, (16)
令
对每个
及
求偏导并令其等于0,可得
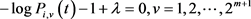 , (17)
, (17)
和
. (18)
所以
,则有
, (19)
故当
是均匀分布的时候,单样本网络熵能取到最大值,此时有
. (20)
2.2. 探测临界点
1) 针对某种复杂疾病,收集该疾病已有的多个样本,并将该疾病对应的全基因组映射到STRING (STRING数据库是一个搜寻已知蛋白质之间和预测蛋白质之间相互作用的系统)的蛋白质–蛋白质相互作用网络。
2) 针对某个未知状态的样本,将该样本分别与每个已知样本建立状态网络。
3) 局部化全基因组状态网络。
4) 计算每个局部化状态网络的单样本网络熵。
5) 将所有局部状态网络的单样本网络熵排序并取前10%的平均值作为差异评价指标。
3. 主要结果
3.1. 仿真网络
本文利用11个结点网络生成疾病的仿真数据,然后利用新开发的算法探测疾病发展过程的临界点。这种类型的基因调控网络常常应用于研究基因转录、翻译等影响基因调控的活动。利用MM (Michaelis-Menten)方程并加入基因自身的降解率,可以得到11个结点的仿真网络,对应的微分方程组为:
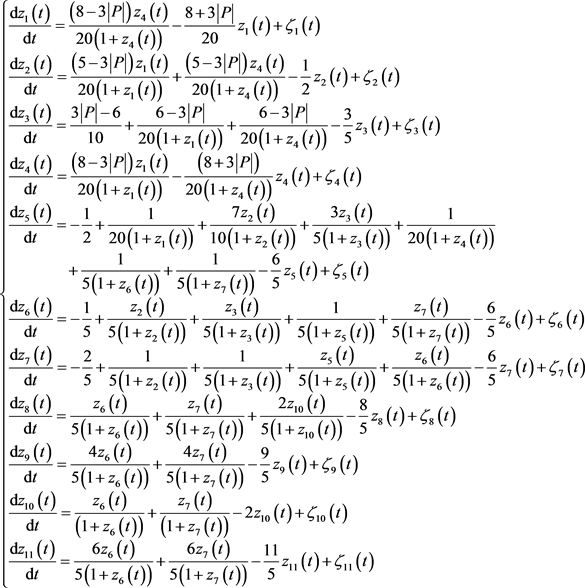 (21)
(21)
其中P为数值控制参数,
是均值为0的高斯噪声,
为第i个mRNA的浓度,11个mRNA的自降解率分别为
。微分方程组(21)完全
体现了仿真网络之中结点间的调控关系,并且有一个稳定点:
. (22)
将微分方程组(21)利用一个小
进行差分化,然后用
代表差分方程组的雅可比
矩阵,有
, (23)
其中A为微分方程组(21)线性主部的系数矩阵,A的11个特征值分别为:
, (24)
所以当
时平衡点
是稳定的,当
时,系统便失去了稳定性,并且系统状态会经
历一个临界转变。
现在将雅可比矩阵J进行对角化,先引入可逆矩阵S:
, (25)
使得
,对于
有:
,(26)
即
是个对角矩阵。现假设
的特征值
对应的特征向量分别为:
.(27)
注意到变量
与最大的特征值
相关并且最接近1,因此,当P趋于0时,主特征值
趋于1,系统发生临界转变。又根据:
, (28)
可知
中的四个变量
和
是直接与主特征值对应的
相关的,根据2.1节的理论推导可知,
构成了11个结点仿真网络系统的主要部分,即相当于真实数据中的动态网络生
物标志物。
基于本文新开发的算法,收集11个仿真结点的时序列数据,并将算法应用于数值模拟数据得到的结果如下图1:
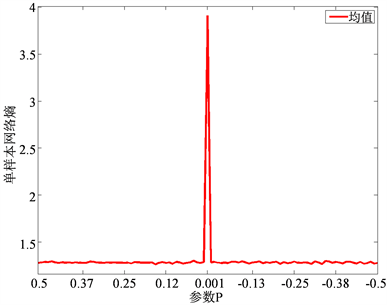
Figure 1. Curve: result of algorithm applied to simulation network data
图1. 算法应用于仿真网络数据结果曲线
3.2. 真实数据
实验数据是从NCBI的GEO数据库(https://www.ncbi.nlm.nih.gov/geo/)下载得到,数据编号为GSE2565。氯化羰(光气)是一种有毒的工业化合物,人或小鼠暴露于光气之中会产生肺水肿和不可逆急性肺损伤,令CD-1雄性小鼠全身暴露于空气(控制组)和光气(实验组)之中,并分别在暴露0.5、1、4、8、12、24、48、72小时后提取小鼠肺部RNA以获得基因表达浓度,实验中观测到在GSH还原转化进入氧化型GSSG的过程起非常重要作用的GPX-2在暴露4到12小时的时候基因表达显著增加,表现出显著性 [15] 。根据小鼠肺光气实验数据,利用本文基于单样本开发的新算法,得到单样本网络熵在第4小时显著增加并达到峰值,即探测到的临界点为第4个时间点,得到的结果与实验观测吻合,真实数据的结果如下图2:
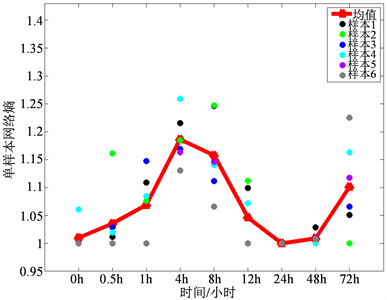
Figure 2. Curve: result of algorithm applied to data GSE2565
图2. 算法应用于数据GSE2565结果曲线
4. 讨论
本文思考传统方法的局限性,创新性地将单样本地方法与熵进行结合,提出了一种新的有效稳定的预警复杂疾病临界点的方法。基于小鼠肺光气实验数据,本文开发的算法成功探测出了第四个时间点为临界点。复杂疾病比如前列腺癌、肝癌、肿瘤等等对人类健康造成巨大的威胁,而能够成功探测出复杂疾病即将恶化的信号,便能帮助人类及时预防甚至治疗复杂疾病,本文开发出的新算法是传统方法的一个突破。
本文仍然有不足之处,比如为了使模型简单,只讨论了线性化系统系数矩阵的特征值全不相同的这一种情况,并没有考虑有重根和共轭复根时算法的效果,这是以后需要改进的一个主要方向。
基金项目
广州市科技计划珠江科技新星专项项目资助(No. 201610010029)。