1. 引言
Joag-Dey和Proschan (1983, [1] )提出了PA (positive associate)随机变量在可靠性理论和多元统计分析中有广泛的应用。经验似然是由Owen (1988)提出的一种非参数推断方法 [2] [3] ,其有类似Bootstrap的抽样特性。这一方法与传统的统计方法比较有很多优点。比如:用经验似然方法构造置信区间拥有域保持性,变换不变性,置信域的形状由数据自行决定,以及Bartlett纠偏性和无需构造轴统计量等等。因而在相依情形下,经验似然方法研究成果少见 [4] - [10] ,尤其在PA相依样本见之甚少。目前,关于分布函数的研究多数局限于非参数核方法。本文将尝试在PA相依样本下,攻克普通经验似然方法的缺陷,重新利用分组经验似然方法,构造未知的分布函数置信区间。首先给出PA序列概念。
定义1: [1] 称随机变量
(
)是PA的,如果对于集合
的任何两个不相交的非空子集
和
,都有
此处,
与
是任何两个使得协方差存在的对每个变量均非降(或非升)的函数。称随机变量序列
是PA序列,如果对任何
,随机变量
(
)都是PA (正相协)的。
若
为来自总体
的正相协样本,由于
,
经验似然
对数经验似然为
。
此处
,且满足
。
2. 主要的结论及其证明
条件:
1)
是来自总体的强平稳PA样本;
2) 令
,若对某个
,满足
,
3)
;
定理1:如果上述条件成立,我们有
。
此处
,
。
然而
和
未知,定理1的结果不能应用,为了攻克这一缺陷,下面利用分组经验似然方法,重新构造经验似然比函数。
记
,其中
表示取整,
为简单起见,使
。
令
(对任意的
)
由于
的强平稳性,
有共同分布函数
,对应经验分布函数
。分组经验似然比为
。
对数经验似然比为
。
此处
且满足
。
定理2:在定理1的条件下,我们有
,
。
利用定理2,当样本
比较大时,可构造未知的分布函数
的置信水平为
的渐近置信区域:
,其中
为
分布的上
分位点,例如
取0.05或0.01。
引理1:记
,有
。
证明:由于
有界,易得
。
引理2: [7] 若
为PA变量,有
,且
,
。令
,
,假设对某个
,
,则
。
引理3: [11] 设
是强平稳PA序列,并且
,假定
,
,则
收敛,且有
,其中
为标准正态分布。
引理4:设
是强平稳PA序列,则有
。
其中
。
证明:令
,利用引理2和条件2有
此处
为某个正常数,不同的地方
取值可不同。
因此有
。
由于
利用引理3和文献 [12] 知
。
综上可得
。
定理1的证明:
由于
, (3.1)
这表明0是集合
所构成的凸包的内点,
因此
存在为正。 (3.2)
观察到
, (3.3)
对上式右端对
求上确界时,满足
。
利用拉格朗日乘子法,可得
。 (3.4)
此处
,且满足
(3.5)
再利用引理3知:
,利用引理2得
。(3.6)
令
满足
,
利用(3.6)式及引理1知:
。 (3.7)
则有
。
令
利用(3.6),(3.7)式和引理4可得
。
借助Taylor展开,我们有
,对某正数
有
。
则有
。 (3.8)
再利用引理3知:
,
。 (3.9)
由条件得:
。 (3.10)
又由(3.6)和引理2得
其中
为某个正数,故有
。 (3.11)
综合(3.9)~(3.11)式便得
,
。 (3.12)
定理2的证明:
只需证明
。 (3.13)
观察到
,对上式右端对
求上确界时,
满足
。
借助拉格朗日乘子法得
, (3.14)
此处 ,且满足
,且满足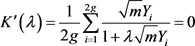 。
。
利用引理1证明得 。 (3.15)
。 (3.15)
有 。 (3.16)
。 (3.16)
 。 (3.17)
。 (3.17)
展开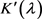 得
得 (3.18)
(3.18)
此处 。
。
利用引理4得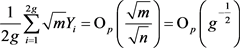 。 (3.19)
。 (3.19)
利用(3.18)及(3.19)式得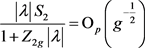 。 (3.20)
。 (3.20)
又由引理1,引理2,(3.17)及(3.20)式知 。记
。记 。
。
利用(3.17)和(3.18)式得: 。 (3.21)
。 (3.21)
又展开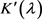 可得
可得
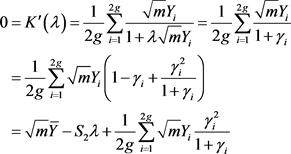 。
。
记 ,有
,有 。 (3.22)
。 (3.22)
利用引理4和(3.18)式得
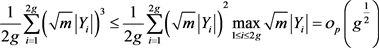 。 (3.23)
。 (3.23)
又利用(3.21),(3.22)和(3.24)式得
 。 (3.24)
。 (3.24)
利用(3.23)式并利用Taylor展开式,则有
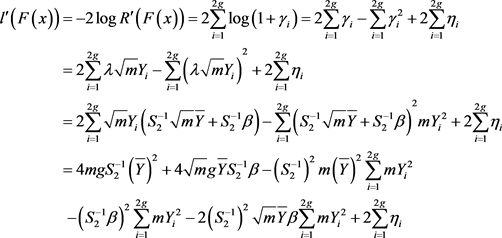
 (3.25)
(3.25)
此处 。
。
利用引理3及引理4,得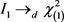 ,
, 。 (3.26)
。 (3.26)
利用(3.24)式得 。 (3.27)
。 (3.27)
利用(3.18)和(3.24)式得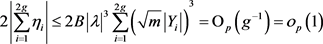 ,
,
从而可得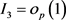 。 (3.28)
。 (3.28)
综上(3.25)~(3.28)式得 ,
,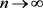 。 (3.29)
。 (3.29)
基金项目
本论文得到广东省自然科学基金项目资助(2016A030313812; 2018A030307070)。