球类物体在空气中飞行阻力的应用研究

The Investigation about the Flying Drag Force of Sphere Type Body

摘要: 通过对羽毛球飞行时的力学分析，对球类(羽毛球)运动中的一些现象做出了理论解释。通过实验，得出某羽毛球的飞行阻力系数。在此基础上，对羽毛球的飞行现象做出了理论分析，并用Matlab做出数值计算。结果表明，数值结果与实际现象较为吻合。此项研究成果可推广到其它飞行物体中。

Abstract: Due to the mechanical analysis of a flying bbadminton, some phenomena of the badminton sports were discussed and the theoretical explanation is presented. The experiments on the drag coefficient of the flying badminton were conducted. Based on the experiments, the badminton flight phenomenon was analyzed via the commercial software of Matlab. The results can be expanded into the other field and it can be added in the teaching process of fluid dynamic or the other class.

1. 引言

羽毛球运动是世界上广泛开展、竞赛频繁的体育运动之一。自从一九九二年列为奥运会项目以来，比赛更加激烈，运动水平得到进一步发展 [1] [2] [3] [4] 。羽毛球在比赛中其最高时速可达332公里 [5] 。在羽毛球比赛中，经常会出现一个很有趣的现象，运动员打出速度很快的平高球时，眼看球飞向边界，但是，往往在到达边界不远处时，羽毛球却迅速的减速下落，并不会出界 [6] 。网上有一些解释，却往往是很定性的分析。另外，现今发表的文章大都关注于羽毛球的训练及发展等方面 [7] ，鲜有对羽毛球运动的力学分析方面的探讨 [8] [9] [10] 。本文经过查询资料，再结合实验，给出准确解释，同时通过对羽毛球飞行规律的探讨，认识和掌握羽毛球飞行的受力规律，为今后的进一步研究提供基础 [11] [12] [13] [14] 。

2. 控制方程

羽毛球在飞行过程中，受两种外力作用，其一为重力，方向向下，大小为mg，m为羽毛球质量，g为地球表面重力加速度；其二为空气对羽毛球的阻滞作用，方向为羽毛球运动方向相反，假设大小为 $f$ 。按地面水平方向与重力方向建立坐标系，设羽毛球飞行方向与地面水平夹角为 $\theta$ (见图1)。

Figure 1. The analytical layout of the flying badminton

图1. 羽毛球力学分析图示

设羽毛球水平位移为 $S_x$ ，竖向位移为 $S_y$ ，由牛顿第二定律可知：

$\{\begin{array}{l}m\frac{{\text{d}}^2{s}_x}{\text{d}{t}^2}=f\cdot \cos \theta \\ m\frac{{\text{d}}^2{s}_y}{\text{d}{t}^2}=f\cdot \sin \theta +mg\end{array}$ (1)

其中，由流体力学理论知道 [15] ， $f=-\frac{1}{2}{C}_d\rho v^2$ ， $\rho$ 为空气密度，取值为1.225 kg/m³、 $v$ 为动体相对于空气的速度绝对值、g取9.8 kg∙m/s²、m为动体质量。另外， $\theta$ 为飞行速度方向与水平方向夹角， $\cos \theta =\frac{v_x}{\sqrt{v_x^2+v_y^2}}$ ， $\sin \theta =\frac{v_y}{\sqrt{v_x^2+v_y^2}}$ 。将流体作用力代入方程(1)，另外，把变量由位移代换为速度，方程(1)可以化为：

$\{\begin{array}{l}m\frac{\text{d}{v}_x}{\text{d}t}=-\frac{1.225}{2}{C}_d\left(v_x^2+v_y^2\right)\frac{v_x}{\sqrt{\left(v_x^2+v_y^2\right)}}\\ m\frac{\text{d}{v}_y}{\text{d}t}=-\frac{1.225}{2}{C}_d\left(v_x^2+v_y^2\right)\frac{v_y}{\sqrt{\left(v_x^2+v_y^2\right)}}+mg\end{array}$ (2)

令 $\frac{1.225C_d}{2m}=c$ ，则方程可化为：

$\{\begin{array}{l}\frac{\text{d}{v}_x}{\text{d}t}=-c{v}_x\sqrt{\left(v_x^2+v_y^2\right)}\\ \frac{\text{d}{v}_y}{\text{d}t}=-c{v}_y\sqrt{\left(v_x^2+v_y^2\right)}+g\end{array}$ (3)

其中，羽毛球的阻力系数无法由理论求出，应该由实验确定。为了确定出羽毛球在空气中的阻力系数，本文作者设计了某羽毛球的自由落体实验，即令羽毛球静止下落，由实验过程可知，水平方向速度恒为零，因此，由方程(3)中可知有

$t+\text{const}=\frac{1}{2\sqrt{gc}}\ln \left|\frac{\sqrt{g/c}+v_y}{\sqrt{g/c}-v_y}\right|$ ，

代入t = 0时，v = 0条件，可以确定积分常数const ＝ 0，于是，有

$t=\frac{1}{2\sqrt{gc}}\ln \left|\frac{\sqrt{g/c}+v_y}{\sqrt{g/c}-v_y}\right|$ (4)

因此，只要测量出下落后速度与时间关系，则阻力系数就可以直接由公式(4)求出。另外，由于实验中的时间–速度关系与式(4)预测曲线有一定的离散，可以根据最小二乘法原理求出阻力系数。

另外，由公式(4)可以看出

$e^{2\sqrt{gc}\cdot t}=\frac{\sqrt{g/c}+v_y}{\sqrt{g/c}-v_y}$ ，

同时，化简后有

由此式可以知道，当时间增加时，速度有最大值 $\sqrt{g/c}$ ，方向为正(向下)，对此式积分得，

$s_y={\displaystyle {\int }_0^{T}2\sqrt{g/c}\frac{e^{2\sqrt{gc}\cdot t}}{1+e^{2\sqrt{gc}\cdot t}}-\sqrt{g/c}}\text{d}t=\sqrt{g/c}\cdot t-c^{-1}\ln \left(\frac{1+e^{2\sqrt{gc}\cdot t}}{e^{2\sqrt{gc}\cdot t}}\right)$ (5)

由式(5)可知，竖直方向的位移(即羽毛球下落位移)由两方面组成，其一为重力引起的位移 $\sqrt{g/c}\cdot t$ ，以最终速度 $\sqrt{g/c}$ 匀速增加；另一方面由阻力引起，以极快的方式趋于零。即只在开始时对位移有影响(抵消重力引起的位移)，随着时间增加，此部分位移迅速变为零，而动体则作匀速运动。

3. 实验结果

实验采用“沉球法”进行羽毛球的阻力系数测量，羽毛球采用“迎客松”牌77#球，球重4.8~4.9克之间 [16] ，取其均值4.85克，共进行了四次实验，实验数据见下表1。

Table 1. Test data

表1. 实验测量数据

四组数据计算结果如表2。

Table 2. The velocity result of the test

表2. 实验测量速度结果

根据表2结果，本文对阻力系数取平均值，则阻力系数为4.382 × 10⁻³。这个结果为文献 [17] 推荐使用的值1.87 × 10⁻³的2.34倍，原因可能为羽毛球的性质不同而造成的。

4. 数值计算

根据前述分析及试验数据，假设羽毛球飞出时的速度为100 m/s，角度为10度，Matlab数值分析可知，其空间飞行轨迹图像如图2所示。从图中可以看出，羽毛球在刚开始时，水平位移与竖向位移同步增加，其比值与速度分量的比值相同，而到达羽毛球轨迹后期，羽毛球竖向位移减少，相应的物理意义是羽毛球已经开始下降，这时，羽毛球水平位移增长极其缓慢，在整个羽毛球下落的过程中，其水平位移增量非常有限。

图3(右)为羽毛球飞行时的速度与时间图像，可以看出，水平及竖向速度在一开始是按指数下降，这与公式(4)的预测是吻合的。速度几乎在0.1秒内就迅速下降到10 m/s以内。

图4为竖向位移与时间图像，可以看出，羽毛球从上升到下落到原点位置，时间不超过一秒钟，实际情况中，羽毛球要下落到比击球点(图中原点位置)要低到地面的距离才停止运动，因此，实际运动时间可能要长一些，尽管如此，其运动时间也是非常少，因此，对运动员的反应要求也比较高。

Figure 2. The plot of velocity vs time

图2. 实验结果速度–时间图

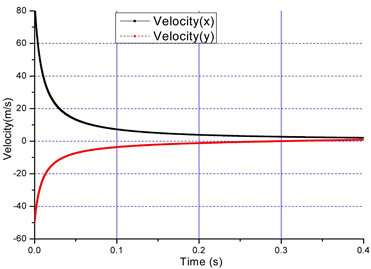
Figure 3. The plot of height vs displacement (left) and velocity vs time (right)

图3. 羽毛球空间飞行图像(左)、速度与时间图(右)

Figure 4. The plot of height vs time

图4. 竖向位移与时间图

图5为水平位移与时间关系图，可以看出，水平位移对时间成对数增长，在开始阶段增长极快，在极短的时间内0.2秒时，位移达到10米，在这么短的时间内，运动员就做出反应，需要长时间的训练与敏捷的反应。另外，从图中同时可以看出，在一段时间后(0.6秒)，位移的增加极为缓慢，也就是说，这时，羽毛球几乎就垂直下落。

Figure 5. The plot of displacement vs time

图5. 水平位移与时间图像

5. 结论

通过以上的分析，可以看出，给出“平高球速度很快但却不会出界”的准确解释，同时，结合实验数据，根据流体力学及相关理论对羽毛球做出数值计算。结果表明，这种计算方法与实际效果还是比较符合的，本文结果可以在流体力学教学中结合实际事例探讨抽象理论的应用，以便达到良好的教学效果；也可以用这种方法对羽毛球的生产或训练做一些指导。

基金项目

国家自然科学基金资助项目(51508238)，江苏省博士后科研资助(1601014B)。

NOTES

^*第一作者。

^#通讯作者。