1. 引言
油气储层岩石受自身沉积、成岩作用,以及受地下非均质应力环境等影响,其渗透率往往表现出明显的各向异性,渗透率是一个矢量。储层在地下环境中,渗透率的各向异性是油气田开发的重要岩石物性参数,它将影响油藏布井方式、井距大小、水平井水平段延展方向、人工压裂方案等。目前有关油气藏数值模拟的软件基本都能处理渗透率各向异性模型。采用渗透率张量对油藏进行描述,能更准确反映油气等流体在地下储层中流动规律,有效提高油藏数值模拟研究精度,为油气藏开发方案及提高采收率措施等提供理论基础,对于指导油气田开发具有重要的意义。
国外早在上世纪30时代就已经开展了对于渗透率方向性的研究 [1] ,上世纪60年代国外已有专门测试渗透率方向性的具体实验方法 [2] [3] [4] [5] 。我国对渗透率方向性研究起步较晚,国内学者们一直都在探索新型的渗透率方向性描述与评价方法 [6] - [16] 。一般认为岩石在一个点不同方向渗透率可以构成如图1所示的椭球体,目前有多种实验测试手段可以得到岩心分别在x,y,z方向的渗透率Kx、Ky、Kz,渗透率各向异性描述方法也是针对这三个方向渗透率值展开的,主要涉及三方面的内容:其一为渗透率各向异性的图示方法,采用恰当的作图方式对各向异性渗透率进行直观描述(图1)。其二为矢量渗透率的平均方法,由于岩心在每一个方向上渗透率都不同,因此需要提取一个特征渗透率值(或视渗透率),代表整个岩心渗透率的大小。最后是渗透率各向异性程度的表示方法,表征不同方向渗透率值的差异程度。
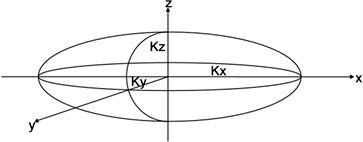
Figure 1. Ellipsoid diagram of vector permeability
图1. 矢量渗透率所构成的椭球体示意图
现有技术一般用如图2所示的柱状图,把三向渗透率放在一起,直观描述渗透率的大小和差异程度 [17] [18] 。

Figure 2. Schematic diagram of permeability anisotropy
图2. 渗透率各向异性图示方法示意图
特征渗透率采用三向渗透率的算术平均表示,即:
(1)
定义
为两向渗透率各向异性系数
(2)
式中Ki,Kj分别为Kx、Ky和Kz中任意两个,用其来描述渗透率各向异性的程度。
定义
为三向渗透率各向异性系数
(3)
用其来描述三向渗透率各向异性的程度 [19] [20] 。
传统渗透率各向异性图示方法由于参数较多,渗透率变化范围大,不利于不同岩心间的比较。
只适用于评价两向渗透率极差。基于算术平均的特征渗透率及各向异性描述方法适用于无相互影响、独立存在的数据体评价,该方式不能体现极值数据点的影响,不适用于存在几何关系的三向渗透率的评价。
针对矢量渗透率的特点,本文提出了新的各向异性渗透率的描述方法,以克服传统方法不能充分体现三向渗透率极值点的影响,物理意义不够明确,且不便于不同岩心间的对比和归类等缺点。
2. 描述岩石渗透率方向性大小的特征值
储层岩石的渗透率是评价储层优劣的主要指标,渗透率的大小则能最直观的反应储层性质。由于岩石的渗透率方向性在地层中受应力影响较为明显,渗透率与应力同为矢量,且一般情况下,Kx、Ky、Kz为不同值,如何用一个特征值来表征渗透率的大小呢?
以往提出的渗透率方向性特征值大都是运用三向渗透率的算术平均值进行计算。我们知道,算术平均值只适合于描述相互独立的多个数据点之间的平均。运用算术平均值推算渗透率方向性特征值时,受极端值影响较大,得出的结果不能够准确表示渗透率的大小。而三向渗透率Kx、Ky、Kz之间是存在相互关系且代表着椭球体在三个轴向上的值。把岩石样品三向渗透率数据Kx、Ky、Kz的几何平均值作为渗透率方向性特征值,受极端值影响较小,能够更加准确的表示渗透率的大小。三向渗透率的几何平均可用下式表示:
(4)
几何平均数考虑了数据间的几何关系,且能更有效反应数据极值的影响,当已知数据呈倍数关系或不对称分布时,几何平均数的效果更好。除此之外,三向渗透率的几何平均还具有明确的物理意义,即为以几何平均数Ka为半径的球体与以三向渗透率Kx、Ky、Kz为半径的椭球体具有相同的体积,如图3所示,而矢量渗透率所包罗的体积能反应该岩石的综合渗透能力,因此用几何平均Ka代表各向异性渗透率的特征值更具有科学性。

Figure 3. Sphere of radius of characteristic permeability Ka
图3. 特征渗透率Ka为半径所构成的球体示意图
3. 三角网状图法描述储层渗透率方向性
三角形统计图是采用数字坐标形式来表现三项要素的数字信息图像。三角形坐标图常用百分数(%)来表示某项要素与整体的结构比例。三条边分别表示三个不同的要素,三个顶点可以看作是三个原点。三角形统计图的适用范围比较广,可用来表示三个项目所占整体的百分比。
已知岩石样品的三向渗透率分别为Kx、Ky、Kz,对其进行归一化可得:
(5)
根据归一化后的三向渗透率值Px、Py、Pz,可在三角图中进行标识,把三个要素体现在同一点上,便于不同岩心之间的比较,表征渗透率各向异性的三角图如图4所示。根据三向渗透率大小之间的关系,渗透率各向异性的三角图可分为3大类区域,每个大类区域又可再划分为两个区域(图4),每个区域点内的三向渗透率大小特征如表1所示。利用这样的原则相比于以往的方法,可以更加有效的描述储层岩石渗透率各向异性情况。

Table 1. Permeability anisotropy triangulation and its characteristics
表1. 渗透率各向异性三角图分区及特征

Figure 4. Depicts the triangular mesh of permeability directivity of the reservoir
图4. 描述储层渗透率方向性的三角网状图
4. 渗透率各向异性程度定量表征
在判断渗透率各向异性的同时,我们还需要知道渗透率各向异性程度的大小。可以利用三向渗透率几何平均与算术平均比值d来代表各向异性程度,即:
(5)
在三角图内分别作出d = 1,d = 0.9,d = 0.7以及d = 0的等值线图,如图5所示。从图中可以看出,在三角形中心点d = 1,此时归一化后的Kx = Ky = Kz,各向同性,在三角形边线上的点d = 0,此时Kx、Ky、Kz中至少有一个为0,三向渗透率变为两向或单向渗透率。在过中心点同一直线上,离中心点距离越远,d值越小,非均质程度越高。可按表2标准对各向异性程度进行评价。

Figure 5. Permeability trigonometric isograms
图5. 渗透率各项异性三角等值线图

Table 2. Triangulation and characteristic of permeability anisotropy
表2. 渗透率各向异性程度三角图分区及特征图
5. 渗透率方向性测试分析及应用
5.1. 方向渗透率仪测量各向异性实验
对取到的其中几组砂岩、碳酸盐岩、页岩样品进行制样处理,如图6所示,利用方向渗透率测试仪(图7)及立方体岩样渗透率各向异性测量流程(图8)分别对砂岩、碳酸盐岩和页岩的渗透率方向性数据进行测试,见表3。

Figure 7. Directional permeability core holder
图7. 方向渗透率岩心夹持器
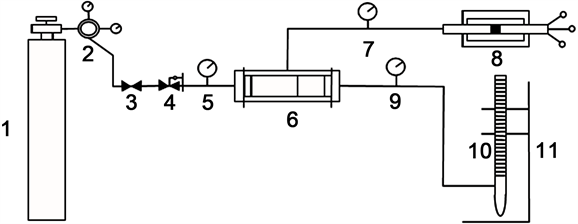 1-气瓶;2-减压阀;减压阀;3-进气阀;进气阀;4-压力调节器;压力调节器;压力调节器;5,7,9-压力表;压力表;6-立方体岩心夹持器;立方体岩心夹持器;立方体岩心夹持器;立方体岩心夹持器;8-恒压泵;10-皂膜流量计; 皂膜流量计;皂膜流量计;11 -铁架台
1-气瓶;2-减压阀;减压阀;3-进气阀;进气阀;4-压力调节器;压力调节器;压力调节器;5,7,9-压力表;压力表;6-立方体岩心夹持器;立方体岩心夹持器;立方体岩心夹持器;立方体岩心夹持器;8-恒压泵;10-皂膜流量计; 皂膜流量计;皂膜流量计;11 -铁架台
Figure 8. Flow chart of permeability anisotropy measurement of cubic rock sample
图8. 立方体岩样渗透率各向异性测量流程图

Table 3. Data of sandstone, carbonate, shale and coal
表3. 砂岩、碳酸盐岩、页岩和煤岩三向渗透率数据表
利用表中数据,作出不同岩类各向渗透率柱状图,如图9所示。从图中可以看出,页岩样品渗透最低,在1 mD以下。砂岩、碳酸盐岩渗透率较高,大于10 mD。但测试样品的各向异性程度无法从柱状图进行判断。因此利用前述方案对渗透率进行评价。

Figure 9. Permeability histogram of sandstone, carbonate and shale samples
图9. 砂岩、碳酸盐岩和页岩样品方向渗透率柱状图
5.2. 渗透率方向性大小和非均质程度评价
利用上述理论中岩石渗透率特征值模型,计算出表3中砂岩、碳酸盐岩和页岩数据的渗透率特征值 、d,见表4,并将其标注在三角等值线图中,如图10所示。

Table 4. Calculation table of permeability directivity and heterogeneity indexes of different samples
表4. 不同样品渗透率方向性大小和非均质指标计算表

Figure 10. Different sample permeability trigonometric isograms
图10. 不同样品渗透率各项异性三角等值线图
从表4计算得到的渗透率特征值可以看出,砂岩、碳酸盐岩样品的渗透率方向性特征值较大,页岩的渗透率方向性特征值较小,则砂岩、碳酸盐岩样品所处地层渗透性明显要优于页岩所处地层的渗透性。同时,结合图4可知,大部分样品都处于II2区域,Kx > Ky > Kz,X方向的渗透率最大。页岩样品9处于Ⅲ1区域,Ky > Kz > Kz,Y方向的渗透率最大。碳酸盐岩样品4处于I2区域,Kz > Kx > Ky,Z方向的渗透率最大,即垂向渗透率最大,造成这一现象的原因大多是因为裂缝或层理的方向。
6. 结论
本文从大小和方向两个方面评价了方向渗透率,该方法克服了无法将三向渗透率统一描述的困难,建立了全新的渗透率方向性评价与描述方法,具有以下优势:
1) 综合岩石的三向渗透率大小提取出描述渗透率大小的特征值,可对不同地层条件的储层或相同地层不同层位的储层渗透率大小进行比较判断;
2) 用三角图对岩石渗透率各向异性进行表征,通过对标点位置可以分析出样品渗透性特征;
3) 利用各向异性程度d和渗透率各项异性三角等值线图可以判断各样品的各向异性程度。
这种表征方法不仅可以判断各向渗透率相对大小,推断优势渗流的方向,还能对比各岩石间渗透率各向异性强弱。相比于利用渗透率的算数平均值描述渗透率各向异性的方法,本文提出的评价方法更加清晰直观,可操作性强,是岩石渗透率各向异性表征方法中较为科学的方法之一,值得使用和推广。