加强凸台的结构参数优化设计

Optimization Design of Structure Parameters of the Strengthening Boss

摘要: 凸台是一种常用的孔边加强方式，本文通过有限元软件ANSYS建立孔边凸台结构模型，分析了一阶和二阶加强凸台结构尺寸对结构静强度和疲劳寿命的影响。通过有限元模型分析，本文以凸台高度、厚度和底部过渡圆角为结构要素，建立了凸台优化设计的方式和原则；在此基础上，结合工程实际，本文给出了二阶凸台设计的方式和原则，且适合于多阶凸台设计。本文的研究结果为孔边加强凸台的结构设计提供了参考和指导，所得结果具有良好的工程参考价值。

Abstract: The boss is a common shape of reinforcement for holes. Based on finite element modeling, this paper established the design principles and procedure for bosses through three fundamental structure elements, i.e. height, width, and transitional fillet radius. The influence of these elements on static strength and fatigue life of the boss was discussed and illustrated. Further, this paper also discussed the design of two-order bosses following the design of general boss above, combined with engineering requirements. The study in this paper is beneficial for engineering, and the demonstration shows optimization of the design which provides the meaningful reference and guidance for design of the hole-side boss structures.

1. 引言

飞机结构中含有各种类型的孔，如翼梁、翼肋及框腹板上的各种孔。由于孔边会出现应力集中，不仅对结构的静强度设计产生重要影响，特别是在疲劳载荷作用下易产生裂纹，从而大大降低了飞机结构的可靠性 [1] 。为了解决这个问题，目前工程上常采用的方式是进行孔边加强，如设置孔边加强凸台。

现阶段凸台结构的疲劳寿命分析还很少，其中周松官等人通过有限元软件Patran和Nastran分析了机加凸台和单侧加强板补强开孔矩形板受面内剪切载荷时的稳定性 [2] ；郑参谋等人采用遗传算法对孔边凸台结构进行基于损伤容限设计思想的优化设计，研究了等重量情况下孔边凸台结构的最优寿命及对应的最佳凸台结构宽厚比 [3] ，继而杜玉梅等人对单边凸台和双边凸台进行了结构断裂品质的对比 [4] 。多数学者致力于通过凸台强度和稳定性研究凸台的优化设计，本文通过进一步研究补强体积变化对寿命的影响，并讨论等补强体积下一二阶凸台的应力关系。

本文借鉴前述学者研究成果 [5] [6] ，基于损伤力学方法，将静强度和疲劳寿命进行综合分析，通过静态强度对凸台结构中内外侧的最大应力进行对比分析，通过损伤计算分析凸台尺寸对疲劳寿命的影响。建立了以补强体积为衡量标准的凸台设计优化原则，并提出了在一定范围内固定补强体积下凸台的优化尺寸，为工程应用提供参考。

2. 计算模型

2.1. 模型参数

考虑到应力集中效应，开口一般为圆形、椭圆形或者带圆角的矩形，通过应力分析不难发现圆形开口对结构强度削弱最小，且圆形开口工艺比较简单，所以开口设计以圆形为佳 [1] ，工程应用中也较为常见，因此本次研究也以此为研究对象。考虑单向受载情况，建立加强凸台的1/4模型，如图1所示，并施加对应的对称边界条件。载荷按照均布应力方式施加，疲劳载荷应力幅值按照100 MPa选取。

对于中部打孔的圆形加强凸台，与应力分布相关的尺寸要素有凸台内通孔半径r、凸台宽度a、凸台厚度h、凸台底边圆角半径r_c、壁板厚度H、壁板尺寸L与W等。考虑到壁板尺寸H、W、L已经确定，凸台内通孔的半径大小r取决于需求大小，则只需要讨论凸台宽度a、厚度h、底边圆角r_c对结构最大应力的影响即可。

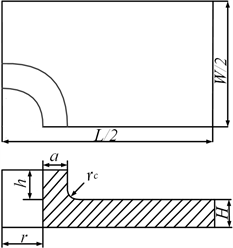
Figure 1. Diagram of the 1/4 strengthen boss

图1. 加强凸台1/4模型示意图

2.2. 有限元模型应力分布

根据图1的模型示意图，使用ANSYS 18.0建立加强凸台的有限元模型，如图2所示，施加均布拉应力(方向参看图3)，对模型进行应力计算和分析，应力分布如图3所示。

Figure 2. Model mesh of the 1/4 strengthen boss

图2. 加强凸台1/4模型网格划分

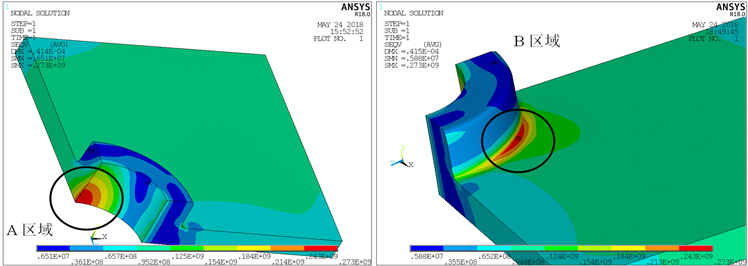
Figure 3. Stress distribution of the 1/4 strengthen boss

图3. 加强凸台1/4模型应力分布

根据加强凸台的有限元分析结果(见图3)可以发现，单向拉伸时结构会出现两处较大应力，一个是加强凸台外侧底部圆角(如图3左图)，以下称为A区域；另一个是通孔内壁底部(如图3右图)，以下称为B区域。显然，加强凸台外侧的底边圆角越大，A区域的最大应力就越小。通过计算发现，只要底面过渡圆角较大，则A区域的最大应力小于B区域的最大应力。由于大过渡圆角有利于加工，因此，设计较大过渡圆角具有良好的可行性，更重要的是，较大过渡圆角使得孔边(凸台内侧)应力最大(即A区域应力最大)，从而简化设计过程。

3. 一阶凸台尺寸计算

对于圆形加强凸台来说，其开口削减材料体积计算式为：

$V=\text{π}{r}^{2}H$ (1)

而加强凸台增加体积与开口削减体积之比为：

$v/V=\frac{\pi \left(r_0^2-r^2\right)\left(H_0-H\right)}{\text{π}{r}^{2}H}=\left(\frac{r_0^2}{r^2}-1\right)\left(\frac{H_0}{H}-1\right)$ (2)

其中r₀为补强圆环的半径，r为原开口的半径，H₀为补强位置的全板厚度，H为原板厚度，该式表达了补强部分与壁板缺失部分的体积比(重量比)。工程设计上r₀均有一定的取值范围，补强有效影响区域为r₀/r = 1.41~2.24范围内，超过此区域补强失效。

3.1. 一阶凸台尺寸的静力分析

分别在不同固定体积比的情况下改变加强凸台的尺寸得到静力加载下最大应力的变化曲线，如图4所示，图中曲线从上至下，补强体积依次为缺口的2、4、6、8、10倍。

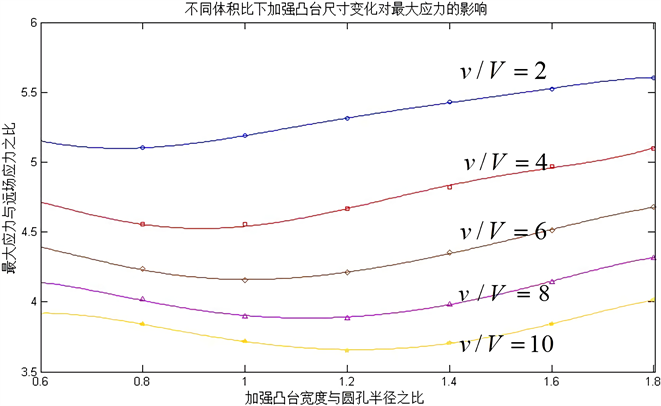
Figure 4. Curve of the boss width, the maximum stress (fixed reinforcement volume)

图4. 加强凸台宽度—最大应力曲线(固定补强体积)

由图4可以看出，每个体积比下都有一个应力极小值，即对应最优凸台尺寸。将上述各最优取值点拟合，可得如下拟合方程：

$\frac{a}{r}=p_1{\left(\frac{v}{V}\right)}^2+p_2\left(\frac{v}{V}\right)+p_3$ (3)

其中p₁ = −0.00464，p₂ = 0.113，p₃ = 0.536。

根据此公式可以找到各补强体积下的最佳凸台尺寸，例如当凸台体积是圆孔(缺失)体积的2~4倍 [1] (工程常用补强体积标准)时，使结构应力最小的凸台宽厚比为2倍左右。另外，若补强体积较大，此时凸台最优宽厚比会有所变化，如补强10倍体积时，最佳宽厚比为1.2。

3.2. 一阶凸台尺寸的疲劳分析

静力分析类似，分别在不同固定体积比的情况下改变加强凸台的尺寸，设定疲劳载荷应力比r = 0，峰值与静载大小相同，使用基于ANSYS二次开发的损伤模拟程序得到一阶凸台的疲劳寿命，结果如图5所示。

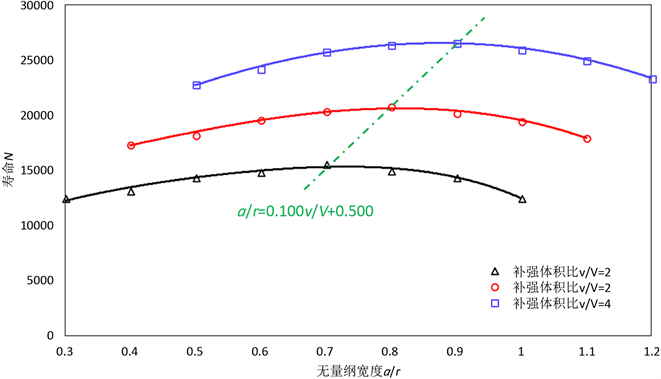
Figure 5. Curve of the boss width-life (fixed reinforcement volume)

图5. 加强凸台宽度—寿命曲线(固定补强体积)

与静力分析相对应，将最优取值点连接并进行拟合分析，寻找最佳的抗疲劳设计尺寸，可以发现拟合结果是一条直线且方程为：

$a/r=0.100v/V+0.500$ (4)

对比式(3)和式(4)可知，在补强体积比为2~4的情况下，疲劳分析的结果与静力分析是基本一致的，综上所述，在进行加强凸台尺寸设计时，可以根据上述的线性拟合公式进行设计计算。

4. 二阶加强凸台的优化

二阶凸台参数

在形式上，可以认为二级凸台是在一阶凸台的基础上设计的，在相同体积比下二阶凸台可以假设为将一阶凸台右上角承受应力较小的部分补回凸台右下部而形成的，如图6所示。

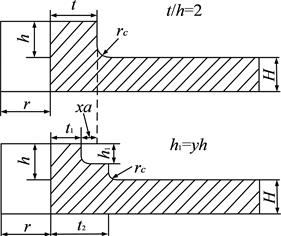
Figure 6. Comparison of primary and secondary bosses (equal volume)

图6. 一级凸台和二级凸台对比图(等体积)

在二阶凸台中，一级凸台宽为t₁，高为h₁，二级凸台宽为t₂，其中考虑到凸台的主要功能，一级凸台多为装配台阶，其尺寸应根据装配需求具体设计，所以说设计关键主要在于第二级。通过设计不同的比例参数y，可以得到不同尺寸的二级凸台，而其最大应力的变化结果如图7所示。

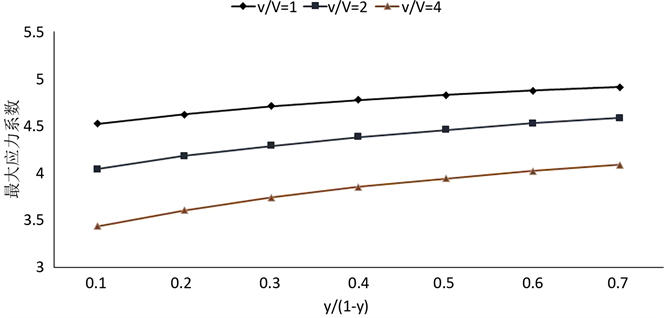
Figure 7. Maximum stress curve for different size secondary bosses (equal volume)

图7. 不同尺寸二级凸台的最大应力曲线(等体积)

图7中三条线分别为1、2、4倍的补强体积情况下的最大应力，可以看出，随着一级凸台尺寸不断增大，凸台的最大应力有所增加。从前面的讨论可知，在补强体积不大时，宽高比在1~2范围内时，凸台宽度加大对应力的减少作用大于凸台高度加大的作用。除非考虑装配需要，一般不要将一级凸台尺寸设计得过大即可。

5. 结论

本文基于损伤力学方法对飞机壁板上的加强凸台进行了尺寸分析，基于静强度和疲劳寿命建立了凸台设计的优化准则，提出了不同情况下凸台的具体优化尺寸，并对多级凸台的设计进行了探讨，为工程应用提供参考，具体结论有以下几点：

1) 在孔边加强凸台结构中，凸台有明显的降低结构应力的作用，也有明显地改善结构力学特性的效果，另外为避免过大的应力集中，加强凸台的过渡圆角半径设计应以r_c > 0.3 h标准设计；

2) 在等重量情况下，凸台结构疲劳寿命与凸台宽厚比之间的关系呈现一定的规律，在结构设计中寻找最佳宽厚比尤显重要，对于本文研究的圆形加强凸台结构，当补强体积为2~4倍时，最佳宽厚比约为2，此时得到结构最优疲劳特性；

3) 二阶凸台的外形轮廓尺寸可以参照对应体积的一阶凸台最优尺寸的选择，在保持同体积条件下，二阶凸台的阶梯尺寸对最大应力的影响不大；

4) 装配用台阶应首先根据装配需求设计，相应的圆角设计也应首先满足装配要求，在此基础上再进行优化设计。