1. 天文信号处理模式发展过程
天文信号的处理模式经过三个典型阶段地心说 [1] 、日心说 [2] - [7] 、大爆炸假说 [8] - [15] 的发展,天文信号的处理模式转换条件,旧模式处理存在诸多无法克服的困难,和体系矛盾。随着观测结果的精密化、远距离化,否定旧体系的内容越来越多,催生新处理模式出现。
托勒密的地心说(古代的天真派):看到天文信号,就是天文现象,就是天象本质,没有虚假。如托勒密的地心说,站在地球上,没有看到地球的运动,看到太阳、月亮、星星都围绕地球运动。根据观测结果综合出均轮、本轮的太阳、行星、月亮、星星围绕地球运动模型,如图1所示。地球是宇宙中心、其它天体都围绕地球运动的地心说。

Figure 1. Ptolemy (geocentric theory), Copernicus (heliocentric theory), Hubble (Big Bang) stood on the earth, observing and interpreting astronomical information
图1. 托勒密(地心说)、哥白尼(日心说)、哈勃(宇宙大爆炸)站在地球上,对天文信息观测与诠释示意图
哥白尼的日心说——理性求真模式:站在地球上,地球的运动是观测不到的。如同站在离开港口的大船上,没有观察到大船的运动,却看到港口、沿岸物体都在后退,它们的后退速度是大船运动的反映。同理,太阳、行星、星星都绕地球运动,是地球自转运动的反映。天空大背景运动反映出地球自转、绕太阳公转运动,如图1所示。哥白尼对天文信息通过理性处理,得到地球、行星绕太阳为中心的运动模型。后来牛顿发现万有引力,彻底证实哥白尼的日心说。
宇宙大爆炸的多普勒效应模式:哈勃用2.54米口径光学望远镜,测量到遥远河外星系发来的光信号,谱线向红光一端移动,简称为红移。红移量与距离成比例的哈勃定律,如图1所示。遥远星系光信号的红移问题,用光源后退的多普勒效应的模式处理,导致星系后退、宇宙膨胀、宇宙大爆炸结论。哈勃认为星系光信号红移形成的原因,用1842年多普勒来解释,得到星系退后的速度:
(1)
式中,Vf——星系远离的速度,HC——哈勃系数;D——星系距离
依此得到宇宙膨胀、宇宙的年龄、暗物质、暗能量等结论。
地心说到日心说,几乎是同样天文信息,只是处理模式不同。获得天文诠释结论相反。宇宙大爆炸的处理模式是否有问题,只有选取更合理的处理模式后,进行对比,才能更好地发现其模式弊端。三种模式如图1所示。
2. 信道天文学:天文信号的信道模式处理
用现代通信模型 [16] - [30] 处理天文信号 [31] [32] [33] [34] ,如图2所示。信道的作用:就是传递信号。但是信道对信号有衰减、失真、噪声、色散等作用,也就是说接收信号与输入信号是不一样的。目前文天信号没有考虑信道的传播影响,因此,其结论的真实性值得怀疑。

Figure 2. Processing astronomical signals using modern communication models
图2. 用现代通信模型处理天文信号示意图
天文信号用信道处理,可用2式表示
(2)
式中,
——信宿(接收端)收到的信号;
——信号源发出的信号;
——信道传递函数,它与传输媒质、传输距离、信号频率、信号强度等参数有关,是一个非常复杂的函数。有时可以简化。
——噪声,式中t——时间参变量;x——信道长度、空间参变量。
由收到的天文信号,在噪声扣除后,经过信道的传递函数逆向处理,可追溯的信号源的发射的原始信号。
(3)
这一处理过程:简称为信道天文学。
3. 宇宙红移的信道模式处理
如果信号源:
(4)
式中,
——恒星、星系发射的信号;A——信号的振幅;
——信号源的角频率,t——时间变量。而信道稳定时的频率响应:传递函数的特征描述。发射源:恒星或遥远的河外星系;信道:光波、电磁波在太空传播的过程、传播的路径,用信道来简化;信宿:地面接收器或卫星接收器。天文信号发射、传播、接收过程可用图2表示。
在现代通信工程中,信道都有媒质:如同轴电缆、光缆、双绞线、大气等构成,对信号吸收、损耗、色散等影响。信号强度、振幅随信道长度按指数规律衰减。
(5)
(6)
式中,
,
分别为信道输出端、入射端的信号强度、或功率密度;
,
分别为信道输出端、入射端的信号振幅;α——衰减系数,x——信道长度、空间自变量。
假定频率随信道传播距离也按指数规律衰减,则有
;
(7)
式中,fo,
信道输出端频率、波长;fs,
信道输入端频率,波长;αf——信道的频率衰减系数;x——信道长度。
天文学上,Z红移通常用波长相对变化量表示
(8)
用信道频率衰减式7代入8式
(9)
红移很小时,近似表达式:
(10)
式中,Z——红移量;αf-——频率随传播距离衰减系数;x——传播距离;
——信宿接收到的信号波长;
——信源信号波长;fo——信宿端信号频率;fs——信源端发射的信号频率。式10与哈勃实测关系式吻合,只是命名以及含义有所区别。
试验测量:红移的试验数值预估
哈勃系数:H0 = 75 km/s/Mpc。
1 Mpc = 106 pc = 3.2616 * 106 l.y. = 3.2616 * 106 * 0.94607 * 1016 m = 3.08568 * 1022 m;
光速1c = 3 * 108 m/s
估算出每一米太空距离,频率或波长相对变化量是:
H1 m = 0.8 * 10−26/m (11)
由于波长、频率变化微小,可以进一步简化
(12)
频率的变化量
(13)
换算成相位角积累
(14)
当取信道长度:D = 20 km;
信号源频率fi = 1015 Hz/s;
哈勃系数:H = 0.8 * 10−26/m;
时间长度一天,
= 86,400 s。
估算频率衰减引起的相位角积累值:
= 360˚ * 86400 s * 0.8 * 10−26/m * 2 * 104 m * 1015 Hz/s = 5˚(15)
实验结构如图3所示,李萨图可以显示输入与输出信号的相位角变化,但是度数不准确缺点。采用波长环,对应0~360度刻度,指针可以在波长环上滑动,用空间相位角来表示信号李萨图的相位角。校对零点:一开始,需要调整波长环指针,Lisa在输入同一正弦波信号时,显示一条直线。按图示接入信号,Lisa图显示信号源与信宿信号的相位角差值,滑动波长指针,李萨图显示相位角零度,这是读出波长环转动的角度就是Lisa图要测量的度数。然后换算成频率、波长的相对变化量、即红移。
用2万米75-5同轴电缆,20 MHz高频信号、20多级宽带中继放大器,测量到波长增加,实验如图3所示。但是实验的重复性不够稳定。水黾产生波纹更容易观察到波纹变宽,波长变长的所谓红移现象。
4. 超新星信号的信道模式处理
超新星信号的特点:作用时间短,持续数天到数月或几年的时间内;信号非常强大:是整个星系的能量总和,是太阳的1010~1012倍。因此,可以看做脉冲函数。收到的信号可以看作脉冲函数对信道的冲击响应。
收到的超新星信号,2011年获诺贝尔物理奖得主的研究成果,如图4所示,超新星亮度比预期小、红移比预期大,推理出宇宙加速膨胀的结论。
信道的传递函数,一般微分方程的表达式
(16)
脉冲函数定义,超新星发出信号可以看做脉冲函数
(17)
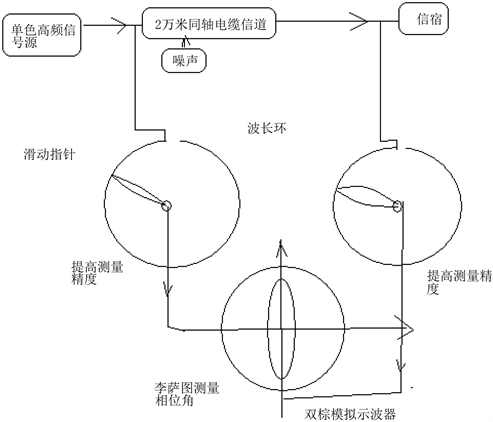
Figure 3. Experimental diagram for measuring frequency attenuation
图3. 测量频率衰减的实验原理图

Figure 4. Supernova signal observations (copy reference)
图4. 超新星信号观测图(拷贝参考资料)
如果A = 1,它称为单位脉冲函数。
二阶信道模式,二阶信道,输入与输出关系式
(18)
其传递函数
(19)
1) 临界阻尼状态响应:
(20)
2) 过阻尼状态
(21)
3) 欠阻尼状态
(22)
用二阶信道,脉冲响应实测图,用简单临界阻尼响应函数拟合,如图5所示。
(23)

Figure 5. Fitting with the second order channel critical damping impulse response function
图5. 用二阶信道临界阻尼脉冲冲击响应函数拟合
与实测拟合曲线非常吻合,也说明太空信道具有二阶信道特征。
2011年诺贝尔获奖者成果:发现超新星亮度比预期的低、红移比预期的大
4.1. 亮度比预期低的信道解释
稳定信号源作用信道:自由空间内,信号源发射电磁波以球面波形式向外传播,亮度与距离成距离平方反比关系
(24)
式中,M——绝对星等;m——视星等;F10——距离10 pc是恒星亮度,Fd——恒星在距离d处的亮度。d——距离(单位pc)。
超新星暴发的信号为脉冲信号形式,接收端收到信号看作是脉冲函数对信道的冲击响应。在时间上、或径向上展开。
导致信号强度降低,即亮度降低。如图6所示。
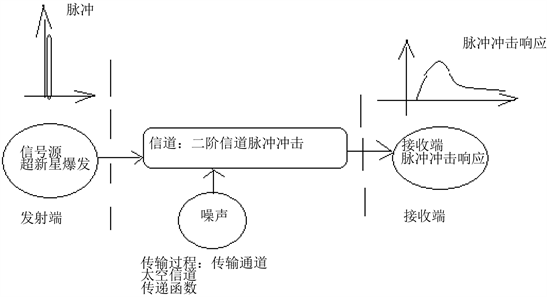
Figure 6. Impact response of pulse function to channel
图6. 脉冲函数对信道的冲击响应
4.2. 红移比预期的大
信道使频率衰减,满足关系式
红移很小时,可近似表示为
超新星暴发的信号为脉冲信号形式,接收端收到信号看作是脉冲函数对信道的冲击响应。在时间上、或径向上展开。
脉冲信号被展宽,频率降低,波长增长。红移量比稳定信号作用信道是大。
5. 信道对波的弥散作用
脉冲波在传播过程中,与连续波传播有区别,存在弥散效应,空间上占据更大的空间,时间上,占据更长的时间段,如图7所示。

Figure 7. Dispersion diagram of wave pulses by channel
图7. 信道对波脉冲的弥散示意图
6. 结论
天文信号的信道模式处理后,更能反映天文现象。遥远星系的红移处理成信道作用,信道使频率衰减。超新星信号经过信道处理,超新星爆发时间更短,传播过程光亮度衰减比恒定光源信号衰减快,红移量也大。
天文信号的信道模式处理结果:星系不用后退,宇宙不用大爆炸,宇宙更不用加速膨胀。宇宙红移仅是光信号在信道中的传播特性。机械波也有波长变长的传播特性,如水波、声波可通过试验观察,电磁波波长随传播距离也有极其缓慢的增长,试验可以验证。
参考文献