关于李雅普诺夫第二方法的教学探究

Teaching Exploration of Lyapunov’s Second Method

摘要: 李雅普诺夫第二方法在自然科学研究中有着广泛的应用。大多数的本科生常微分方程教材只是简单地叙述了这种方法，但是对于李雅普诺夫函数的构造方法和具体形式并没有给出详细的介绍。鉴于此，作者归纳总结几种常用的构造方法和形式，为教学提供参考。

Abstract: Lyapunov’s second method is widely used in natural science research. Most undergraduate text-books of Ordinary Differential Equations simply describe this method, but the construction method and form of Lyapunov function are not been introduced in detail. In view of this, the author summarizes several commonly used construction methods and forms, which provides a reference for teaching.

1. 引言

随着人类认识、改造和利用自然能力的不断提高，以及实际应用的需要，人类面临大量非线性问题的处理。在研究过程中，专家学者们发现微分方程理论是处理非线性问题行之有效的工具之一。为了培养研究非线性科学问题方面的接班人，《常微分方程》基础课的教学就起着至关重要的作用。由于在实际系统中不可避免地会出现各种偶然的外干扰，这些干扰往往会影响系统的稳定性，而且只有稳定的状态或过程才有现实意义，所以研究描述实际系统的微分方程解的稳定性对自然科学有着重要的意义和价值。因此，解的稳定性是《常微分方程》教材中非常重要的内容之一。在过去的几十年里，国内外已经出版了许多经典的《常微分方程》教材，例如文献 [1] - [9] 。

李雅普诺夫在他的“运动稳定性的一般问题”中创立了处理微分系统稳定性问题的两种方法：第一方法是运用微分方程的级数解，在此之后没有得到很好的发展；第二方法是在不求微分方程解的情况下，借助一个所谓的李雅普诺夫函数 $V\left(t\right)$ ，并通过微分方程所计算出来的导数 $\text{d}V\left(t\right)/\text{d}t$ 的符号性质，就能直接推断出解的稳定性，因此又称为直接法。由于国内大多数本科生的《常微分方程》教材中对如何构造李雅普诺夫函数未给出详细的方法，为了弥补这一不足，作者将归纳总结几种李雅普诺夫第二方法中V函数的构造方法和形式，为教学提供了参考。

2. 李雅普诺夫第二方法

本节我们简单地叙述李雅普诺夫第二方法。考虑如下自治微分系统

$\text{d}x/\text{d}t=f\left(x\right),x\in R^N,$ (1)

其中 $f\left(x\right)=\left(f_1\left(x\right),f_2\left(x\right),\cdots ,f_N\left(x\right)\right)$ 在区域 $\left|x\right|\le M$ 上连续且满足初值问题解的存在唯一性条件， $f\left(0\right)=0$ 。假设存在一个标量函数 $V\left(x\right)$ 在区域 $\left|x\right|\le M$ 上有定义且具有连续的偏导数。下面给出两个定义：

1) 若 $V\left(0\right)=0,V\left(x\right)>0\left(<0\right)$ ，当 $x\ne 0$ ，则称V为定正(负)函数；

2) 若 $V\left(0\right)=0,V\left(x\right)\ge 0\left(\le 0\right)$ ，当 $x\ne 0$ ，则称V为常正(负)函数。

下面简单地介绍李雅普诺夫的稳定性准则。

定理2.1 李雅普诺夫的稳定性判别法：

(C₁) 若V是定正(负)函数且 $\text{d}V/\text{d}t|\left(1\right)$ 为定负(正)函数，则系统(1)的零解是渐近稳定的；

(C₂) 若V是定正(负)函数且 $\text{d}V/\text{d}t|\left(1\right)$ 为常负(正)函数，则系统(1)的零解是稳定的；

(C_.) 若V和 $\text{d}V/\text{d}t|\left(1\right)$ 均为定正(负)函数，则系统(1)的零解是不稳定的。

3. V函数的构造

在应用李雅普诺夫第二方法判断微分系统解的稳定性和渐近稳定性时最大的困难就是如何构造合适的V函数和具体形式。本节将简单地归纳并研究出几种常用的构造方法和形式。

3.1. V函数的构造方法1

对于自治系统，判断其零解的稳定性和渐进稳定性可以构造如下形式的V函数：

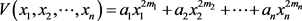
其中 $a_1,a_2,\cdots ,a_n$ 同号， $m_1,m_2,\cdots ,m_n$ 和n都是正整数。这样构造的V函数都是定号函数且不含t。

例1：考虑下列微分系统零解的稳定性

$\stackrel{\dot{}}{x}=-x^5-y^3,\stackrel{\dot{}}{y}=x^3-y^5$

解：令 $V\left(x,y\right)=x^4+y^4$ ，显然V是定正函数。计算其沿着系统的全导数，可得

$\text{d}V/\text{d}t=-4x^8-4y^8$

为定负函数。则由定理2.1可知上述系统的零解渐近稳定。

例2：考虑二阶微分方程 $\ddot{x}+\stackrel{\dot{}}{x}+x=0$ 零解的稳定性。

解：上述二阶微分方程等价于

$\stackrel{\dot{}}{x}=y,\stackrel{\dot{}}{y}=-x-y$

取函数 $V\left(x,y\right)=x^2+y^2$ ，显然V是定正函数。计算其沿着系统的全导数，可得

$\text{d}V/\text{d}t=-2y^2$

为常负函数。则由定理2.1可知零解是稳定的。

3.2. V函数的构造方法2

对于非自治系统，判断其零解的稳定性和渐近稳定性往往找不含t的函数 $V\left(x\right)$ ，用这类函数的优点在于其具有无限小上界，然而这类函数只适用于简单的运动方程。如果用含有t的李雅普诺夫函数 $V\left(t,x\right)$ 时，其中 $t_0$ 可以取任意大，此时条件满足就可以了。

例3：讨论如下微分系统

$\stackrel{\dot{}}{x}=-a\left(t\right)\left(x^2+y^2\right)x+b\left(t\right)y,\stackrel{\dot{}}{y}=-b\left(t\right)y-a\left(t\right)\left(x^2+y^2\right)y$

零解的稳定性，其中 $a\left(t\right),b\left(t\right)$ 为连续函数，对于 $t\ge t_0$ 。

解：取函数 $V\left(x,y\right)=x^2+y^2$ ，显然V是定正函数且具有无限小上界。计算其沿着系统的全导数，可得

$\text{d}V/\text{d}t=-2a\left(t\right){\left(x^2+y^2\right)}^2$ .

1) 当从某一时刻 $t=T\ge t_0$ 之后都有 $a\left(t\right)\ge 0$ ，则 $\text{d}V/\text{d}t$ 是常负函数。根据定理2.1可知零解是稳定的。

2) 当从某一时刻 $t=T\ge t_0$ 之后都有 $a\left(t\right)\ge A>0$ ，则 $\text{d}V/\text{d}t$ 是定负函数。根据定理2.1可知零解是渐近稳定的。

例4：考虑如下微分方程零解的稳定性

$\stackrel{\dot{}}{x}=-\sin \left(tx\right)$ .

解：取函数 $V\left(t,x\right)=0.5x^2+1-\cos \left(tx\right)$ ，显然V是定正函数。计算其沿着系统的全导数，可得 $\text{d}V/\text{d}t=-t\sin {\left(tx\right)}^2\le 0$ ，当 $t\ge 0$ 。

根据定理2.1可知零解是稳定的。

3.3. V函数的构造方法3

对于线性常系数微分系统 $\text{d}V/\text{d}t=AX$ ，有如下结论：

1) 若其特征根 ${\lambda }_j$ 均有 ${\lambda }_i+{\lambda }_j\ne 0,i,j=1,2,\cdots ,N$ ，则对任何负(正)定对称型矩阵C均有唯一的二次型 $V\left(X\right)=X^{\prime }BX$ 使得 $\text{d}V/\text{d}t=X^{\prime }CX$ ，其中矩阵B满足 $B=B^{\prime }$ 和 $A^{\prime }B+BA=C$ 。

2) 若其特征根均具有负的实部，则 是正(负)定的。如果系统特征值有正的实部，则V不是常正(负)的。

例5：考虑下列线性常系数微分系统

${\stackrel{\dot{}}{x}}_1=x_2,{\stackrel{\dot{}}{x}}_2=-2x_1-3x_2$ .

解：系数矩阵 $A=\left[\begin{array}{cc}0& 1\\ -2& -3\end{array}\right]$ 的特征值 ${\lambda }_1=-1,{\lambda }_2=-2$ ，满足 ${\lambda }_1+{\lambda }_2\ne 0$ 。对于对称矩阵 $C=\left[\begin{array}{cc}-4& 0\\ 0& -1\end{array}\right]$ 。由 $A^{\prime }B+BA=C$ 可计算得 $B=\left[\begin{array}{cc}4& 1\\ 1& \frac{1}{2}\end{array}\right]$ 。根据上述方法，可以得到二次型

$V\left(x_1,x_2\right)=4x_1^2+2x_1{x}_2+\frac{1}{2}{x}_2^2$ .

显然可知V是定正函数。根据定理2.1可知上述系统的零解是渐近稳定的。

注1．判定微分系统非零特解的稳定性，一定要作变量替换，把非零特解转化成新系统的零解，然后用李雅普诺夫第二方法来判定其稳定性。

4. 总结

由于国内大多数本科生的《常微分方程》教材中对如何构造李雅普诺夫函数未给出详细的方法，为了弥补这一不足，作者归纳总结了三种李雅普诺夫第二方法中V函数的构造方法和形式，为教学提供了参考。此外，作者发现应用这三种方法和形式能够解决大部分的课后习题以及相关考研试题，所以它们完全适用于本科生学习，对高校教师进行《常微分方程》教学有着一定的帮助，这也进一步补充和完善了这方面的教学内容。如有不妥之处，请予指正。

基金项目

安徽省重大教学改革研究项目(2016jyxm0254)；安徽理工大学教学改革研究项目。