1. 引言
软磁性纳米结构的基态通常由交换能和偶极能间的相互竞争以及形状决定 [1] 。为了减少偶极能,纳米尺寸的圆盘形成了磁矩沿着薄膜面内涡旋状闭合排列,靠近盘中心的磁矩则转向至垂直于盘面方向以减少交换耦合能,我们称这种磁矩状态为磁涡旋态 [2] 。磁涡旋态具有稳定的拓扑磁性结构,其磁矩垂直于盘面的区域被称作涡核。涡核磁矩朝上或朝下,相应地可以定义两种涡核极性
。通过翻转涡核极性,可以实现二进制信息的写入,有希望应用于高密度磁存储和高速磁性随机存储器。
给磁涡旋态施加一个面内激发磁场时,可以激发出低频旋进模式(<1 GHz)和高频角向自旋波模式(≥1 GHz) [3] 。涡核极性可以通过施加脉冲磁场 [4] 、交变磁场 [5] 或者自旋极化电流 [6] 等激励手段来翻转。Matthias Kammerer [7] 等人提出在高频的面内磁场下,涡核极性的翻转是由角向自旋波模式和涡核旋进模式共同作用完成的。在面内磁场作用下,涡核从盘中心沿着螺旋线路径运动,被逐渐加速到每秒几百米的速度,直到涡核–反涡核对产生和湮灭,导致涡核翻转。涡核的大幅度移动会对磁存储器的读取产生一些障碍。给磁涡旋态施加一个垂直于盘面的激发磁场时,可以激发高频径向自旋波模式(~10 GHz)。当所加振荡外磁场频率调到径向自旋波模式的本征频率时,涡核极性翻转所需的临界场比静态垂向磁场小一个数量级,且涡核极性的翻转速度也会大大提高 [8] [9] 。在垂向磁场下,可以实现磁涡旋态极性的原位翻转(即涡核始终位于圆盘中心),更利于磁存储器中信息的读取。王振宇 [10] 等人进一步提出施加一个相位匹配的共振外磁场来驱动涡核极性的翻转,使涡核极性的翻转速度得到大幅度提高,且翻转所需的时间随着本征模式阶数的增加而持续降低。
在过去研究中圆盘厚度通常不超过10纳米。圆盘厚度越大,其动力学会越复杂。A. O. Adeyeye [11] [12] [13] 等人对厚纳米圆盘做了诸多工作,给厚纳米圆盘进行宽频铁磁共振测量,发现圆盘厚度足够大时,会出现更加复杂的高阶回旋模式,即在圆盘涡核处厚度方向产生节点。随着圆盘厚度的增加,角向自旋波模式不仅会与低阶回旋模式发生混合,还会与高阶回旋模式发生混合 [14] 。在本文中,我们发现当圆盘厚度不可忽略时,垂向脉冲磁场不仅激发出了常见的径向自旋波模式,还激发出了厚度方向的驻波模式与径向自旋波模式的混合模式。对于这种混合模式,随着本征频率的增加,厚度方向的节点数不变,径向的节点数逐渐增加。随着圆盘厚度增加,高阶径向自旋波模式还会与厚度方向的高阶驻波模式发生混合,形成更加复杂的自旋波模式。我们给圆盘施加混合模式下的全域垂向共振磁场时,圆盘中磁涡旋态的极性很难发生翻转。而给圆盘施加混合模式下相位匹配的垂向共振磁场时,圆盘中激发共振自旋波的效率要远远高于空间均匀分布的外磁场。因此,涡核极性不仅更容易发生翻转,且翻转所需的时间随着外磁场振幅的增大而减少。
2. 模型及初始态分析
我们采用LLG软件进行微磁模拟。样品模型为直径300纳米、厚度20纳米到90纳米(间隔为10纳米)的一系列坡莫合金(permalloy)纳米圆盘。在数值计算中,所取的分割单元为2.5 × 2.5 × 2.5 nm3到3 × 3 × 4 nm3不等。样品采用坡莫合金材料的常用参数,即饱和磁化强度设为8 × 105 A/m,交换作用常数A为1.3 × 10−11 J/m,磁晶各向异性系数为0,吉尔伯特阻尼系数α为0.01。所有的磁涡旋态的初始涡核极性均设为向上(p = 1)。图1(a)和图1(b)展示了厚度为20纳米和80纳米的圆盘涡旋态的初始磁化强度在z方向上分量的分布图。我们可以看到当圆盘厚度为20纳米时,涡核直径在厚度方向上基本一致。而圆盘厚度为80纳米时,圆盘厚度方向的不同层中磁矩分布有很大的区别。此时,圆盘中间层的涡核直径比靠近盘面处的涡核直径要大得多,呈现中间大两头小的橄榄球状,且在涡核外围区域存在着mz略小于0的区域。
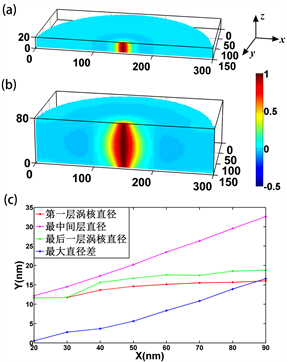
Figure 1. Magnetization distribution of initial vortex states in permalloy nanodisks with diameter of 300 nm and thickness of 20 nm (a) and 80 nm (b), respective. For simplicity, only one half of the nanodisk is displayed. The color bar shows the z-component of magnetization. (c) Variation of vortex core diameter and the biggest diameter difference, in the bottom, middle and top layer, with respect to the sample thickness
图1. 直径为300纳米,厚度分别为20纳米(a)及80纳米(b)的坡莫合金纳米圆盘中磁涡旋态沿着厚度方向的初始磁化空间分布图(为方便起见,仅显示了半个圆盘区域),色彩条状图代表磁化强度在z方向上的分量。(c)涡核在圆盘底层、中间层和顶层的直径及最大直径差随圆盘样品厚度的变化关系
我们将涡旋态中心区域磁矩的垂向分量
的区域定义为涡核,其中
是涡核中心处磁矩的垂向分量。涡核的形状通常接近圆形,因此我们用涡核的直径来定义涡核的尺寸。涡核的尺寸随着纳米圆盘厚度的变化发生改变。在图1(c)显示了不同厚度的圆盘中涡旋态的涡核直径在厚度方向上的变化图。当圆盘厚度大于20纳米时,涡核直径在厚度方向上明显非均匀分布。涡核最大直径(即圆盘中间层涡核直径)随着圆盘厚度的增加呈线性增加。圆盘第一层(即圆盘底层)和最后一层(即圆盘顶层)的涡核直径均随着圆盘厚度的增加而缓慢增加,而圆盘最后一层的涡核直径要比圆盘第一层的涡核直径要更大一些,涡核不再沿着厚度方向对称分布。在厚度方向上的最大直径差(即圆盘中间层与第一层的涡核直径差)也随厚度的增加越来越大。
涡核直径沿着厚度方向的不均匀性与圆盘中各能量项的分布密切相关。图2为厚度分别为20纳米、50纳米及80纳米的圆盘初始态在沿着直径的剖面上各个能量项的空间分布。在没有外场的作用下,总能量主要由交换能和退磁能组成,主要分布在涡核区域。当圆盘厚度为20纳米时,可以观察到交换能在厚度方向上基本均匀分布,中间区域交换能略小于靠近盘面区域的能量。比交换能小很多的退磁能更多分布在靠近圆盘表面的区域,圆盘总能量呈现靠近圆盘表面的能量略大于圆盘中间层的能量。如图1(c)所示,厚度为20纳米的圆盘中间层涡核的直径要略大于圆盘两端涡核的直径。而厚度为50纳米和80纳米的圆盘,涡核均呈现两头小中间大的橄榄球状。当圆盘厚度为50纳米时,中间层的交换能明显小于圆盘表面的交换能,退磁能也主要分布在靠近圆盘表面的区域,从而造成中间层的总能量比圆盘表面的总能量小的多。当圆盘厚度为80纳米时,能量主要聚集在圆盘上下两端,中间层交换能与靠近盘面区域交换能的差异变得更大。
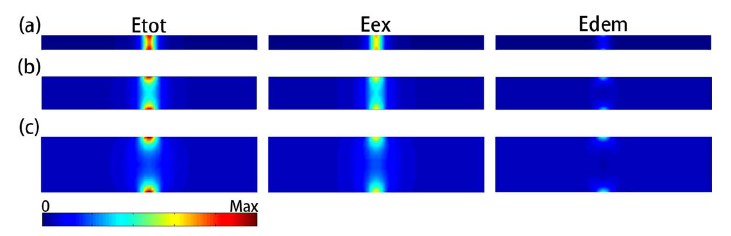
Figure 2. Spatial distribution of the total, exchange and demagnetization energy in a cross section along a diameter in nanodisks with thicknesses of 20 (a), 50 (b), and 80 nm (c), respectively. The color bar denotes the relative magnitude of energies
图2. (a)、(b)和(c)分别是厚度为20纳米、50纳米和80纳米的圆盘中总能量、交换能和退磁能在沿着直径的垂直剖面上的空间分布。色彩条状图表示能量大小
3. 自旋激发频谱分析
当圆盘的厚度为20纳米时,微磁模拟计算中样品分割单元大小为2.5 × 2.5 × 4 nm3。给圆盘施加沿厚度方向的全域方形波脉冲磁场,然后记录圆盘的磁化强度随时间的变化,通过傅里叶变换得到圆盘中涡旋态振动频谱如图3(a)所示。用n代表径向自旋波模式的节点数,在频率50 GHz范围内可以观察到高达n = 9径向自旋波模式,各阶径向自旋波模式在样品第一层的FFT振幅空间分布如插图所示。除了这几个常见径向自旋波模式的共振峰之外,还观察到了额外的峰。这些额外峰对应的振动模式在样品第一层的FFT振幅空间分布如图3(b)所示。我们发现这些特殊模式与径向自旋波模式非常类似,在半径方向上产生节点,并被分割n个相位交替变化的区域,但其频率均在30 GHz以上,比对应阶数的径向自旋波模式的频率要大的多。这些特殊模式除了在圆盘径向形成节点,在圆盘的厚度方向同样形成了节点。我们将厚度出现的节点数用TS = n (Standing wave-thickness modes,n为节点数)表示 [15] 。
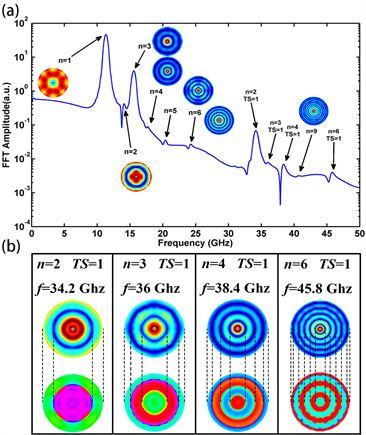
Figure 3. (a) The FFT amplitude spectrum of a nanodisk with diameter of 300 nm and thickness of 20 nm, after excitation of a pulse square field applied along z direction. The inset shows spatial distribution of FFT amplitude of radial spin wave modes in the bottom layer of the nanodisk. (b) Spatial distribution of FFT amplitude and phase of mixed spin wave modes in the bottom layer of the nanodisk
图3. (a) 直径为300纳米,厚度为20纳米圆盘在沿z方向施加方形脉冲磁场作用下的振动频谱,插图为各阶径向自旋波模式在样品的第一层中FFT振幅的空间分布。(b) 混合自旋波模式在样品第一层的FFT振幅和相位空间分布
图4(a)为各阶径向自旋波模式在沿着直径的垂直剖面上FFT振幅和相位的空间分布,可以观察到在厚度方向上振幅和相位的分布基本是均匀的,且沿着中心对称。在n = 9、f = 40.7 GHz的模式的节点处可以清楚地看见围绕中间层的某些点相位有360˚的改变,而且从圆盘中心到边缘的相邻节点的相位变化方向相反。这种相位的变化在其它阶数的径向自旋波模式中也存在。在采用2.5 × 2.5 × 4 nm3的分割单元进行模拟计算时,圆盘在厚度方向被分割的层数为单数。分析这些特殊模式在厚度方向的变化时,中间层的相位变化是不均匀的,缺乏准确性。所以我们又采用2.5 × 2.5 × 2.5 nm3的分割单位重新做了微磁模拟,结果得到振动频谱与2.5 × 2.5 × 4 nm3分割单元的情形类似,共振频率值与图3(a)所示略有区别,同时n = 3、TS = 1的模式不见了(在原本的样品中该模式下的FFT振幅就非常小),其它几个额外峰对应的模式在厚度方向上FFT振幅和相位的空间分布如图4(b)所示。我们观察到沿着圆盘直径方向和厚度方向均有相位在节点两侧的突变。随着本征频率的增加,圆盘厚度方向的节点数并没有增加,但是径向的节点数在逐渐增加。这些额外峰对应的模式实际为径向自旋波模式与厚度方向驻波模式的混合模式。
对于厚度为30纳米的圆盘,所取微磁模拟分割单元为3 × 3 × 3 nm3。给圆盘施加沿厚度方向的全域方形波脉冲磁场后,通过对圆盘的磁化强度随时间的变化做傅里叶变换得到的涡旋态振动频谱如图5(a)所示。在频率50 GHz范围内可以观察到高达n = 7径向自旋波模式。这些径向自旋波模式的FFT振幅和相位在沿着直径的剖面上的空间分布如图5(b)。FFT振幅分布在沿着直径的剖面上开始出现了些许的差别。尤其是n = 1的径向自旋波模式,在靠近涡核外围的中间层出现了振幅很小的区域。与20纳米厚的圆盘类似,FFT相位环绕中间层的节点有360˚的改变,且圆盘中心到边缘的相邻节点的相位变化方向是相反的。

Figure 4. Spatial distribution of FFT amplitude and phase of radial spin wave modes (a), and mixed spin wave modes (b),in a cross section along a diameter of the nanodisk with diameter of 300 nm and thickness of 20 nm. The color bars on the lower left and lower right represent the FFT amplitude and phase, respectively. Use the color bars in all amplitude and phase profiles
图4. 直径为300纳米、厚度20纳米的圆盘径向自旋波模式(a)、混合自旋波模式(b)的FFT振幅和相位在沿着直径剖面的空间分布。左下色彩条状图代表振幅强度,右下色彩条状图代表相位,在所有的振幅和相位图中均使用该色彩条状图

Figure 5. (a) FFT amplitude spectrum of a nanodisk with diameter of 300 nm and thickness of 30 nm. The inset shows spatial distribution of FFT amplitude of radial spin wave modes in the bottom layer of the nanodisk. (b) Spatial distribution of FFT amplitude and phase of radial spin wave modes in a cross section along a diameter of the nanodisk
图5. (a)直径300纳米、厚度30纳米圆盘的振动频谱。插图为各阶径向自旋波模式在样品的第一层中FFT振幅的空间分布。(b)各阶径向自旋波模式的FFT振幅和相位在沿着直径剖面的空间分布
在厚度为30纳米的圆盘振动频谱中同样发现了额外的峰值:(n = 1, TS = 1, f = 20.6 GHz),(n = 2, TS = 1, f = 22.2 GHz),(n = 3, TS = 1, f = 24.7 GHz)和(n = 4, TS = 1, f = 26.7 GHz)的混合模式。其FFT振幅和相位的空间分布如图6所示。与厚度为20纳米的圆盘相比,厚度为30纳米的圆盘的混合模式不仅频率范围更低,而且只是在涡核外围的厚度方向出现了节点。
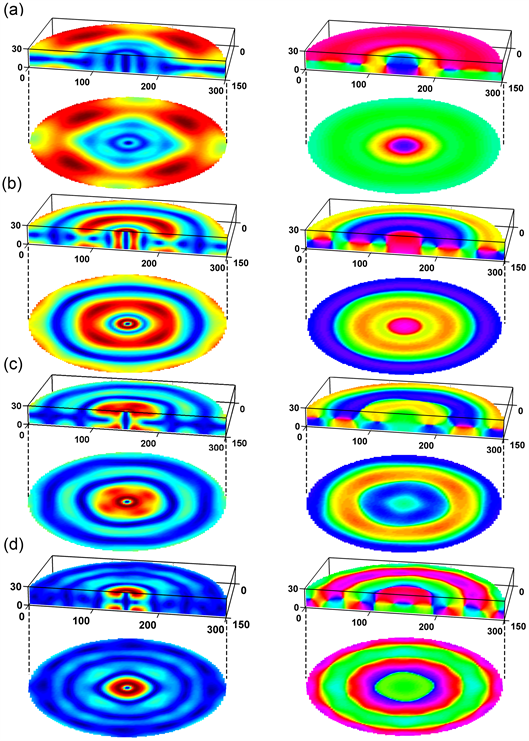
Figure 6. Spatial distribution of FFT amplitude and phase of mixed spin wave modes of a 30 nm thick nanodisk. The number of nodes along the thickness is TS = 1. The numbers of nodes along the radial direction are n = 1, 2, 3, and 4 for (a), (b), (c) and (d) respectively.The FFT amplitude and phase images are displayed underneath the cross sections images
图6. 厚度为30纳米圆盘中的各混合自旋波模式的FFT振幅和相位的空间分布图。在厚度方向上节点数均为TS = 1,半径方向上的节点数分别为(a) n = 1,(b) n = 2,(c) n = 3,(d) n = 4。在剖面图下展示了样品第一层的FFT振幅和相位图
当圆盘厚度增加为40纳米时,厚度方向上均匀分布的径向自旋波模式难以出现,出现更多的是径向自旋波模式与厚度方向上驻波模式的混合态。在频率低于35 GHz时,与厚度为30纳米的圆盘类似,产生了涡核外围与径向自旋波模式的混合模式。在f = 36.6 GHz,出现了n = 3、厚度方向上TS = 2的混合模式(图7(a))。随着圆盘厚度的持续增加,所得到的振动频谱范围均在35 GHz以下,均出现了涡核外围驻波模式与径向自旋波模式的混合模式,且发现了厚度方向上的高阶驻波模式。如在厚度为60纳米圆盘频谱图中发现了(n = 3, TS = 2, f = 24.5 GHz)的混合模式(图7(b));在厚度为80纳米圆盘中(n = 3, TS = 3, f = 26.9 GHz)的混合模式(图7(c))和(n = 5, TS = 3, f = 32.2 GHz)的混合模式(图7(d));在厚度为90纳米圆盘中(n = 4, TS = 3, f = 26.7 GHz)的混合模式(图7(e))。

Figure 7. The spatial distributions of FFT amplitude and phase of hybridization of the high-order standing wave with high-order radial spin wave modes in thick nanodisks
图7. 厚纳米圆盘中产生的高阶径向自旋波模式与厚度方向上高阶驻波模式的混合模式下FFT振幅和相位的空间分布图
4. 混合模式下的动力学
为了研究这种混合模式的动力学,我们尝试施加与这种混合模式的本征频率相匹配的垂向共振磁场。对厚度为20纳米的圆盘中(n = 2, TS = 1)的混合模式,施加一个垂向共振磁场,其随时间的变化表示为
,其中f = 34.8 GHz,t = 2000 ps。当对该圆盘施加全域的均匀垂向共振磁场时,磁场振幅H0增加至800 Oe时涡核极性仍然无法翻转。当施加与(n = 2, TS = 1)模式的相位分布相匹配的外磁场时,磁矩振动明显增强,涡核极性的翻转速度会显著提高。在图4(b)的频谱图中,可以观察到该模式被分为六个不同的相位区域。外磁场方向同振动模式的相位分布匹配即意味着,在绿色相位区域和深蓝色区域的外磁场方向相反。
当相位匹配的垂向共振磁场振幅H0为200 Oe时,涡旋态的极性在t = 988 ps发生了单次翻转。随着外磁场增幅的逐渐增加,圆盘磁矩振动更加剧烈,涡核极性会发生多次翻转,且翻转所需时间也会降低。所加外磁场振幅增至300 Oe时,涡旋态的极性在t = 442 ps发生了第一次翻转,比振幅为200 Oe外磁场下翻转所需的时间减少了一半。图8显示了相位匹配的外磁场振幅H0为200 Oe时样品第一层、中间层(即第四层)和顶层(即第八层)涡核极性翻转前后几个时刻的mz三维示意图。可以观察到在t = 200 ps时,中间层的磁矩振动很小,而在第一层和第八层涡核外围的磁矩振动剧烈,且振动相位相反。在t = 976 ps时,第八层的涡核极性已经发生翻转,第一层和第八层涡核外围的磁矩仍为反相分布,中间层的磁矩小幅度振荡。在t = 9880 ps时刻,中间层的涡核极性也开始发生翻转,第一层的涡核正在被压缩。在t = 984 ps,第八层和中间层的涡核极性已经完全翻转,第一层涡核被剧烈压缩。到t = 988 ps,整个圆盘的涡核极性发生完全翻转,即由原本的极性向上变为极性向下。
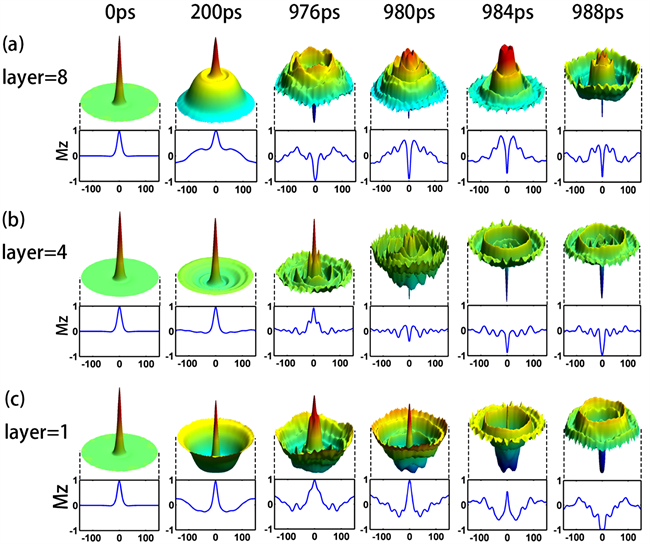
Figure 8. Snap shots of the magnetization dynamics of the top (a), middle (b) and bottom (c) layers of a 20 nm thick magnetic vortex, under the excitation of a phase-matched resonant field
图8. 厚度为20纳米的圆盘在施加一个相位匹配的共振外磁场后,磁涡旋态在顶层(a),中间层(b)及第一层(c)的磁矩变化示意图
对厚度为20纳米的圆盘中(n = 4, TS = 1)的混合模式,我们同样施加一个相位匹配的垂向共振磁场,取(f = 34.8 GHz, H0 = 300 Oe)时,圆盘涡核极性在t = 288 ps发生第一次翻转。对厚度为60纳米的圆盘中(n = 3, TS = 2, f = 24.5 GHz)的混合模式,在厚度方向上出现了多个节点,将圆盘分割为多个相位交替变化的区域,施加振幅为300 Oe的相位匹配的垂向共振磁场时,涡核极性在t = 455 ps发生第一次翻转。在厚度为30纳米圆盘中,只是在涡核外围厚度方向产生节点的(n = 1, TS = 1,f = 20.6 GHz)混合模式,施加振幅为450 Oe的相位匹配的垂向共振磁场时,涡核极性在t = 660 ps发生第一次翻转。我们的结果表明了磁涡旋极性在相位匹配的高频垂向共振磁场下快速翻转,为磁涡旋态随机存储器提供了新的可能性。
5. 总结
本文探讨了当坡莫合金圆盘厚度与半径相比不可忽略时,涡旋态涡核形状的变化,这种中间大两头小的橄榄球状涡核的形成与退磁能与交换能的相互作用密切相关。随着圆盘厚度的增加,交换能在涡核区域的分布差异性越大。
当给这种厚纳米圆盘施加一个垂直于面内的激发磁场时,涡旋态的自旋波激发频谱随圆盘厚度改变而发生变化。随着圆盘厚度的增加,激发模式在厚度方向上不再均匀分布。我们发现在更厚的纳米圆盘中除了常见的径向自旋波模式,还形成了厚度方向的驻波模式与径向自旋波模式的混合模式。随着本征频率的增加,径向的节点数逐渐增加。对于这种混合模式,分为涡核外围厚度方向的驻波模式和厚度方向上均匀的驻波模式两种。我们发现厚度方向上均匀的驻波模式频率(35 GHz以上)要大于涡核外围厚度方向的驻波模式的本征频率(35 GHz以下)。当我们给这些混合模式施加一个相位匹配的高频垂向共振外磁场时可以实现圆盘涡旋态极性的快速翻转。
未来我们将从理论讨论这两种厚度方向的驻波模式差异性的起因、圆盘厚度对高阶混合模式的影响、钉扎边界时是否会出现更加均匀的混合模式等物理因素。
基金项目
本文作者感谢国家自然科学基金项目10974163 和 11174238的支持。