1. 引言
随着用电需求的增加以及电力系统规模的扩大,电力系统在运行过程中有时会出现低频振荡的现象,严重危害系统的稳定运行。从数学角度上来说,电力系统的这种低频振荡现象其实是一种混沌现象。为了抑制系统的低频振荡现象,我们可以在分析了系统的动力学行为的基础上,对系统施加控制,从而抑制混沌行为的出现,最终使系统尽快达到稳定。
在电力系统的动力学行为研究中,简单电力系统模型的动力学行为被广泛研究。如:文献 [1] 研究了电力系统的七阶、六阶、四阶模型的失稳与混沌之间的关系。文献 [2] 研究了电力系统三阶模型的动力学行为,发现了混沌现象和分岔行为。随后许多学者进一步研究了考虑扰动项或时滞等问题的电力系统模型的动力学行为。通过运用诸如多尺度方法 [3] 、自适应无源方法 [4] 、数值模拟 [5] 等不同的方法分析了带有不同扰动项的二阶单机无穷大系统的非线性动力学行为,发现以上系统均出现了混沌现象。文献 [6] 研究了在参数变化时电力系统的四阶时滞模型的分岔行为。除此之外,一些学者分析了某些参数的变化对系统混沌特性的影响,主要包括系统参数中的阻尼系数、功率以及负荷性周期扰动项对系统稳定性的影响 [7] [8] [9] [10] 。在对电力系统的阻尼系数这个电力系统模型中的一个重要参数的研究中,文献 [2] 提出了二阶摆动方程和经典三阶模型在正阻尼条件下,有相似的动力学行为,而在负阻尼条件下,动力学行为截然不同。之前很多文献更多地关注于正阻尼系数对系统动力学行为的影响 [11] [12] ,而对负阻尼研究的较少 [2] ,因此,在研究内容上,本文补充了系统参数同步角速度和负阻尼系数对系统稳定性的影响。
混沌的抑制和控制方法也在不断地增加并改进。文献 [13] 设计出了一种基于微分几何方法的渐近跟踪控制器,该控制器可以消除系统的混沌行为,实现高效地达到渐近跟踪的目的。文献 [14] [15] 分别提出了不同改进后的滑模控制方法,如:模糊控制与滑模控制方法、鲁棒反演滑模法,这些方法也可以达到抑制系统低频振荡的目的。
本文采用了文献 [16] 中的电力系统的三阶数学模型,并利用已有文献 [17] 进一步简化了系统模型,分析了该系统的非线性动力学行为,在控制方案设计上不仅对参数已知时提出了自适应控制与非线性反馈控制两种控制方案,而且针对以前的文献很少考虑参数未知或只考虑一个参数是未知的情况,设计了某些参数是未知的控制设计方案。自适应控制和非线性反馈控制这两种控制方法比较简单,易操作,具有通用性,不仅应用于整数阶系统,并且也可以推广到分数阶系统。本文的总体设计是在考虑负阻尼系数、同步角速度对系统的动力学行为产生的影响上,对参数已知和未知两种情况进行控制器设计。
2. 电力系统三阶数学模型的建立
电力系统是由发电、输电、变电、配电和用电等环节组成的一个复杂的非线性系统,在研究系统的动力学行为和控制之前,必须要选择和建立合适的数学模型。在数学上可以用一组微分方程展示电力系统的非线性特性。为了便于理解与分析,图1给出了一个单机无穷大系统的示意图,同步发电机(G)的功率可以通过变压器电抗(
)和传输线电抗(
)传送到无穷大母线电压(
) [2] 。其中,G代表同步发电机,
是变压器电抗,
是传输线电抗,
表示无穷大母线电压,
表示同步发电机端电压。

Figure 1. Diagram of single machine infinite bus system
图1. 单机无穷大系统示意图
文献 [16] 给出了具有励磁控制的三阶单机无穷大系统的数学模型(1),该模型忽略了d轴和q轴阻尼绕组的动态过程,但考虑励磁的动态变化。该系统的微分方程展示如下:
(1)
式中:
:发电机转子角;
:转子角速度与同步角速度的偏差,即相对转速;E:暂态电势;
:同步角速度;D:阻尼系数;H:惯性常数;
:系统稳态运行时给定的励磁电压;
:发电机的机械功率,该模型其余符号的含义同文献 [16] 第五章。随后进一步简化方程(1) [2] ,可以得到如下数学模型:
(2)
式中:
,
,
,
,
。由于同步发电机的参数B、X、
、
、
在数值计算过程中是固定不变的,但同步角速度
、阻尼系数
、转动惯量H和机械功率
是主要的变化参数 [2] ,并且本文直接考虑
的情况。所以,本文主要研究了
和
的变化对系统稳定性的影响,将其他参数固定取值为:
、
、
、
、
[17] 。因此,得到了相应的数学模型:
(3)
式中:
;
;
;
。本文主要对方程(3)进行研究与讨论。
3. 电力系统三阶模型的稳定性分析
3.1. 参数同步角速度和负阻尼系数对系统的稳定性分析
现在我们将研究参数
的变化对系统稳定性的影响(不失一般性令
,
)。以前的文献为了计算简便,一般只考虑
的情况,本文分别给出了
三种情况下的分岔图和最大Lyapunov指数图。
1) 固定参数
,
,
,改变参数a。
当
时,系统的分岔图和最大Lyapunov指数图如图2所示。由图可知,当
时,系统的最大Lyapunov指数大于0,系统处于混沌状态;当
时,系统的最大Lyapunov指数小于0,系统处于稳定状态。
2) 固定参数
,
,
,改变参数a。
当
时,系统的分岔图和最大Lyapunov指数图如图3所示。同理得到,当
时,系统处于混沌状态;当
时,系统处于稳定状态。
3) 固定参数
,
,
,改变参数a。
当
时,系统的分岔图和最大Lyapunov指数图如图4所示。同理得到,当
时,系统处于混沌状态;当
时,系统处于稳定状态。
因此,观察分岔图和相应的最大Lyapunov指数图,可以得到:从定性上来看,同步角速度
并不影响系统的动力学行为,即不同的
均可以产生混沌、稳定的不动点等丰富的动力学行为,但从定量上来看,不同的
混沌产生的具体区域不同。
接下来分析阻尼系数
对系统动力学行为的影响。不失一般性,我们取参数
,
,
,改变
的取值。对于不同a的典型动力学行为被展示在图5中,从a到d,
。在图5(b)中周期运动是非常小的。
 (a) 系统分岔图
(a) 系统分岔图 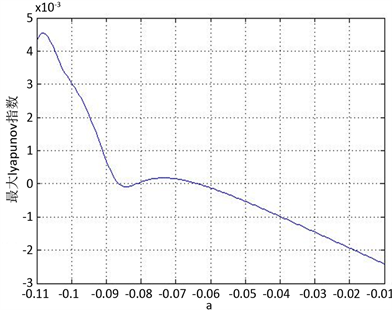 (b) 系统最大Lyapunov指数图
(b) 系统最大Lyapunov指数图
Figure 2. The bifurcation diagram and Lyapunov exponents diagram for
图2.
时系统的分岔图和最大Lyapunov指数图
 (a) 系统分岔图
(a) 系统分岔图 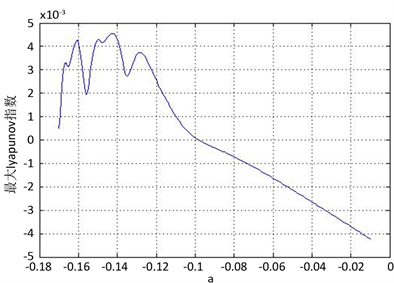 (b) 系统最大Lyapunov指数图
(b) 系统最大Lyapunov指数图
Figure 3. The bifurcation diagram and Lyapunov exponents diagram for
图3.
时系统的分岔图和最大Lyapunov指数图
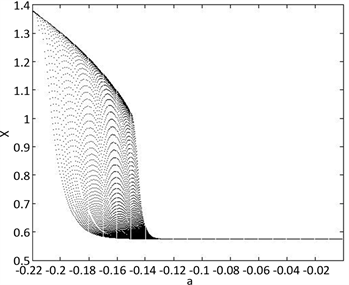 (a) 系统分岔图
(a) 系统分岔图 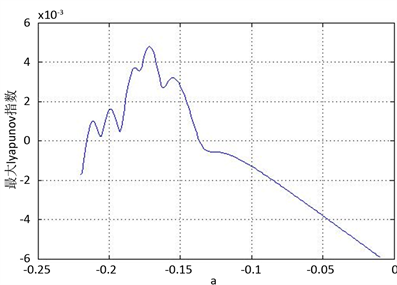 (b) 系统最大Lyapunov指数图
(b) 系统最大Lyapunov指数图
Figure 4. The bifurcation diagram and Lyapunov exponents diagram for
图4.
时系统的分岔图和最大Lyapunov指数图
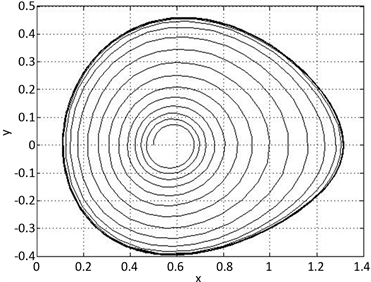
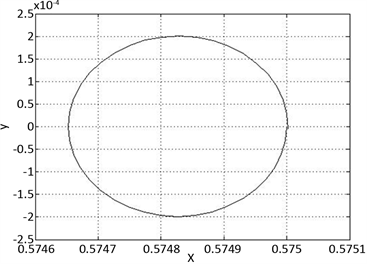 (a) a=-0.01
(a) a=-0.01 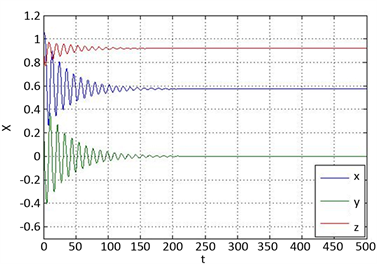 (b) a=-0.0592
(b) a=-0.0592  (c) a=-0.08
(c) a=-0.08  (d) a=-0.1
(d) a=-0.1
Figure 5. Different dynamical behaviors with the change of parameter a
图5. 参数a变化时不同的动力学行为
从图5中可以观察到,如果
,系统处于稳定的平衡点状态;如果
,系统是周期运动;如果
,系统是混沌的;如果
,系统是不稳定的。
以
的情形为例,从图2(a)和图5的图像中,这个系统出现了一些丰富的动力学行为。从右到左,随着a的减少,系统出现了稳定的不动点、周期运动、混沌以及系统的崩溃。我们的分析表明不动点由稳定到不稳定经过了Hopf分岔,在本节的后面会进行具体的介绍。从图2(b),可以确定混沌区域的出现,不同的阻尼系数影响混沌区域的大小和位置。
相同的方法可以用于分析
和H对系统稳定性的影响,在这里主要介绍了参数
和
对系统稳定性的影响。
3.2. 系统的基本性质分析
从以上的分析可以看到,当参数
,
,
,
,系统处于混沌状态。相应的
相图和时序图被展示在图6中。
 (a) x-y相图
(a) x-y相图 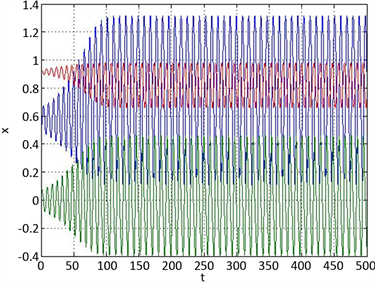 (b) 时序图
(b) 时序图
Figure 6. The phase diagram and time series analysis diagram of the system
图6. 系统的相图和时序图
3.2.1. 耗散性和吸引子的存在性
依赖MATLAB仿真,根据wolf算法,可以得到系统(3)的最大Lyapunov指数分别为:
,
,
,根据最大Lyapunov指数
,因此系统处于混沌状态。
考虑系统(3)的向量场散度
,由散度的定义 [18] [19] [20] ,得到
Liouville定理指出了Lyapunov指数和系统Jacobin矩阵(即散度)之间的关系,即
由此我们可以得到:
即
即
这里
表示初始时刻系统的体积,因此,只要
,系统(3)即为一个耗散系统,系统将以指数−0.86收敛到零,并且随着
,
,表明系统(3)的所有轨线将被限制在一个零体积的空间上,表明了吸引子的存在性。
由Kaplan-Yorke猜测,可以得到系统(3)的分维数
(4)
由于分维数不是整数,也表明系统(3)出现了混沌,存在吸引子。
3.2.2. 稳定性分析和分岔理论
基于方程(2)系统的雅可比矩阵可以写成如下形式:
此处
表示方程(2)的平衡点。
解上式代数方程,我们可以得到
假设特征值方程有以下形式:
其中
,
。我们可以得到
进一步,我们得到以下等式:
将上式进行整理化简,即得:
(5)
分岔曲线的方程由以下方程组成:
(6)
4. 三阶电力系统的控制
随着电力系统用电需求的增加以及远距离输电方式的出现,系统会出现低频振荡现象,因此,我们可以设计相应的控制器使系统恢复稳定状态。本节讨论了参数已知时两种控制器设计方案以及参数未知时系统的控制器设计方案。
4.1. 自适应控制器设计
4.1.1. 控制器设计方案
自适应控制是基于自适应控制原理提出的控制设计方案,研究发现,该方法不仅适用于确定性系统,也适用于不确定性系统。现在采用自适应控制方法对方程(3)进行控制器设计。
取
,其中,
,
,
,
表示系统的平衡点。则该系统的受控系统表示为如下形式:
(7)
受控系统(7)在平衡点
处的雅可比矩阵为:
(8)
特征值方程可以表示成如下形式:
(9)
其中,
根据Hurwitz判据可知,当控制参数
、
、
满足如下关系式时,系统(7)可以在平衡点处渐近稳定。即:
(10)
4.1.2. 数值仿真
取系统参数
,
,
,
,控制参数
,
,
,经过计算,系统存在两个平衡点
和
。下面以平衡点
为例进行数值实验。图7表示在自适应控制下系统被稳定在平衡点
处,在相图中,系统从任一初始值出发,均可以被控制在平衡点处,在时序图中系统在4秒左右达到了渐近稳定,由仿真结果可以得到控制器设计的正确性。并且通过计算得到此时满足Hurwitz判据的条件,仿真结果和理论一致。
 (a) 自适应控制下系统相图
(a) 自适应控制下系统相图 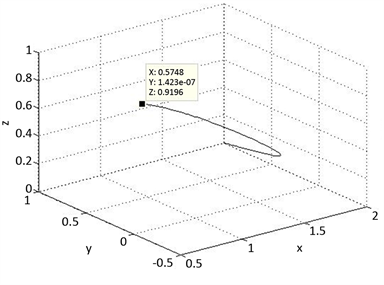 (b) 自适应控制下系统时序图
(b) 自适应控制下系统时序图
Figure 7. Phase diagram and the time series analysis diagram of the system
图7. 系统的相图和时序图
4.2. 非线性反馈控制器设计
4.2.1
. 控制器设计方案
非线性反馈是通过非线性环节而构成的一种反馈方式,一般情况下,采用非线性反馈比采用线性反馈可以获得更好的效果,对简化系统结构也起到一定的作用。下面运用非线性反馈方法对参数已知的情况进行控制器设计。
为了方便讨论,对方程(3)作如下变换:
(11)
其中,
为系统的平衡点,则系统变为如下形式:
(12)
若方程(12)在原点处稳定,则原系统(3)在平衡点
处稳定。
取
其中,
(13)
此处
表示反馈增益,相应的受控系统如下:
(14)
定理:当
,
,
时,系统(14)稳定于原点,从而原系统可以在平衡点
处稳定。
证明:
将方程(13)带入到受控系统(14)中,整理得到
(15)
构造一个Lyapunov函数
取
,
要保证
是负定的,当且仅当以下三个不等式同时成立,即:
,
,
. (16)
因此,当
,
,
时,
是负定的,则系统(14)在原点处是稳定的,原系统可以在平衡点处达到稳定。
4.2.2
. 数值仿真
同样取
,
,
,
,此时考虑平衡点
处的数值试验。取反馈增益
,
,
,初值可以任意取值。从图8的相图中可以看到,系统被很好的稳定在原点,从时序图中发现系统在3秒左右就稳定于原点,同时反馈增益的选取满足定理条件,表明控制器设计的良好性。
 (a) 非线性反馈控制下系统相图
(a) 非线性反馈控制下系统相图 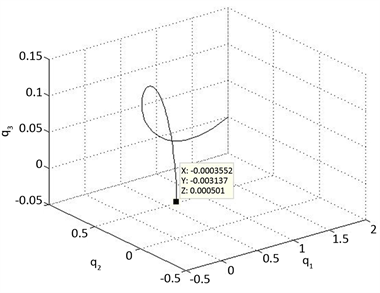 (b) 非线性反馈控制下系统时序图
(b) 非线性反馈控制下系统时序图
Figure 8. Phase diagram and the time series analysis diagram of the system
图8. 系统相图和时序图
4.3. 未知参数控制器设计
4.3.1
. 未知参数控制器设计方案
接下来考虑某些参数未知时,即系统参数a,b,d未知时,控制器设计方案。当参数a,b,d未知,
时,相应的受控系统如下:

取控制器
,
,
。
未知参数辨识律
,
,
。
,
,
,式中
,
,
是未知参数a,b,d的估计值,
,
,
分别表示未知参数a,b,d的误差。
证明:
取Lyapunov函数
,
所以当满足
,
,
的条件时,系统渐近稳定于原点。
4.3.2
. 数值仿真
系统参数
,未知参数实际值
,
,
,控制参数
,
,
。从图9的时序图中可以看到,系统在12秒左右渐近稳定于原点。从图9的未知参数估计值可以得到
,
,
,与实际值相一致,表明控制器与未知参数辨识律设计的正确性。
 (a) x-y-z时序图
(a) x-y-z时序图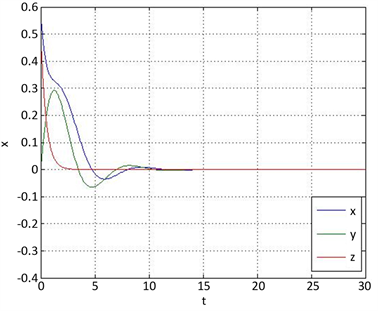 (b) 参数a、b、d的估计值
(b) 参数a、b、d的估计值
Figure 9. The time series analysis diagram with unknown parameters and estimates of unknown parameters
图9. 带有未知参数时系统时序图和未知参数的估计值
5. 结语
本文通过分析电力系统三阶数学模型的分岔图、Lyapunov指数图、相图和时序图,得到了系统参数的变化会影响系统的不动点、混沌、失稳区域的出现并在理论上进行了验证。在此基础上,采用自适应控制、非线性反馈控制和未知参数控制分别讨论了参数已知和未知情况下系统的控制器设计方案,并通过构造Lyapunov函数在理论上证明了三种方案可以使系统达到渐近稳定。本文的理论分析和仿真结果相一致,定性地证明了控制器设计的正确性。论文中的仿真结果都是在MATLAB编程的基础上得出的,程序的设计严格符合相关的定义,因此,仿真结果的准确性和精度是可以保证的。下一步,拟完成相应的分数阶电力系统三阶模型的混沌与控制。本文设计的控制器可以逐渐应用到工程实际中,减少系统的低频振荡,保证系统的稳定运行,因此更适合应用于电力系统的控制与稳定性的研究中。
致谢
首先我要感谢我的导师刘辉昭教授,在学习的道路上给予了我很大的帮助。刘辉昭老师是一个十分谨慎、负责任的导师,对论文中的方程仔细推敲,确保正确无误,对论文中的摘要、引言也提供了很多的意见。导师这种严谨治学以及对科研的认真,深深地影响着我。
其次,我要感谢论文的编辑、审稿人,谢谢你们辛勤的审稿与付出,感谢你们对我的论文提出的各种批评与建议,这些都是促进我不断进步的助力石。
最后,我要感谢我的师姐、师妹以及我的朋友们,非常感谢你们的支持与鼓励。我也要感谢我的父母亲人,正是有你们强大的避风港,我才能在科研道路上不断坚持下去。
我由衷地感谢各位评审专家给予的评审与指导!谢谢!
基金项目
中国国家自然科学基金:11371110。