1. 引言
倒向随机微分方程在金融数学、最优控制、随机决策和偏微分方程等领域中有着广阔的应用前景。经典的倒向随机微分方程是由布朗运动驱动的,1990年Pardoux和Peng [2] 给出了Lipschitz条件下解的存在唯一性结果。然而Lipschitz条件太强,布朗运动太过于理想化,致使倒向随机微分方程的应用受到相当大的限制。因此,一方面,许多学者开始研究各种非Lipschitz条件下的倒向随机微分方程来改进Pardoux和Peng的关于解的存在唯一性,例如,Fan [1] ,Mao [3] ,Lepeltier和Martin [4] ,Kobylanski [5] 分别给出了非Lipschitz条件下解的存在唯一结果。另一方面,有相当多的学者研究了其他干扰源驱动的倒向随机微分方程,其中,李娟 [6] 研究了连续局部鞅驱动的Lipschitz条件下的倒向随机微分方程,王湘君 [7] 研究过由连续半鞅驱动的Lipschitz条件下的倒向随机微分方程。本文中,我们研究了由连续局部鞅驱动的倒向随机微分方程在Fan [1] 中非Lipschitz条件下解的存在唯一性。
2. 主要结果
令
为一个带信息流的完备的概率空间,其中流
满足通常条件,记
为可料 σ 域。
为一个连续局部鞅,并且
,
为M的平方变差过程。
为一个任意固定的数,称为时间区间。
首先给出几个相关记号:
1) 用
表示所有使得
的
-适应的
值的过程
的集合。当
时简记为
。
2) 用
表示所有使得
的
可料的
值的过程
的集合。当
时简记为
。
3) 用
表示所有满足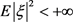 的
-可测的
值的随机变量
的集合。当
时简记为
。
的
-可测的
值的随机变量
的集合。当
时简记为
。
以下,我们将讨论如下形式的一维倒向随机微分方程:
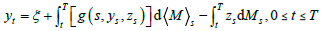 (1)
(1)
其中,
为
适应的过程,
为
可料的过程,
,
为具有零初值的连续局部鞅,具有可料表示性,且
为有界的,即存在正常数
,使得
,a.s.,函数
为
可测的。
假设方程(1)满足以下条件:
(H1)
;
(H2) 存在一个单调不减凹函数
,使得
,
,
其中
,
,
。
(H3)存在一个常数
,使得
,
,
(H4)
;
注1:
是一个单调不减凹函数,且
,即
几乎处处是线性增长的,存在一个常数
,使得对
,有
。
定理1 设函数g满足(H1)—(H4),
,则倒向随机微分方程(1)在
中有唯一的解。
3. 引理
为了证明定理1,我们还需要用到下面的引理。我们首先来构造倒向随机微分方程(1)的Picard逼近序列,由如下的倒向随机微分方程所定义:
, (2)
其中,生成元
满足(H3)和(H4),由文献 [8] 定理4.2得,对
,方程(2)在
中有唯一的解
。
由注1和(H2),容易得
和
引理1 在定理1的假设下,存在一个常数
和常数
,且
只依赖于C,K只依赖于C和T,
使得对任意的
, n,m ≥ 1 ,有
(3)
和
(4)
证明:由方程(2),得
是如下方程(5)在
中的解
(5)
其中
。
由(H2)和(H3),得
(6)
(6)式意味着方程(5)的生成元
满足文献 [1] 命题1中的假设(A),即
,
,
,
。又因为
是一个凹函数,所以由文献 [1] 命题1和命题2,应用Fubini定理和
Jensen不等式,即可得(3)式和(4)式。 证毕。
引理2 在定理1的假设下,存在一个不依赖于
的
,常数
,使得对
,有
。
证明:由定理1的假设,得
即方程(2)的生成元
满足文献 [1] 命题1中的假设(A)。
又因为
是一个凹函数,所以由文献 [1] 命题2,应用Fubini定理和Jensen不等式,存在两个只依
赖于C的正常数
和
,使得对
,有
(7)
其中
令
,
,其中
是引理1中的,A是注1中的,则对 ,有
,有
(8)
由(7)和(8),得
(9)
又因为
是一个单调不减函数,由(9)式,注1和(8)式,得
,
,证毕。
4. 定理1的证明
先证存在性。先定义一个函数列
如下:
(10)
对
,由引理2,得
,
,
。
由数学归纳法,可得
。
因此,对
,函数列
极限存在,记为
。
因为
是一个连续函数,且
,令
,对(10)式取极限,由Lebesgue收敛定理,对
,有
,
,
。
由数学归纳法,可得
即
是cauchy序列,又因为
是一个连续函数,由引理1中的(4)式知,
也是cauchy序列,它们的极限分别记为
和
。令
,对(2)式取极限,可得
是具有参数
的BSDE在
的
解。
可以通过迭代可得,
,方程(1)在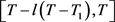 有解,因此可得,方程(1)在
上解的存在性。
有解,因此可得,方程(1)在
上解的存在性。
再证唯一性:设
和
都是方程(1)的
解,则 
是如下方程(11)的
解。
(11)
其中,
。
由(H2)和(H3),可得
,即方程(11)的生成元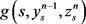 满足文献 [1] 命题
满足文献 [1] 命题
1中的假设(A)。
由文献 [1] 命题1和命题2,存在一个只依赖于C的正常数
和一个只依赖于C和T的正常数
,使
得对
,有
(12)
和
。 (13)
对(12)式应用Bihari’s不等式,得
,因此
,再由(13)式,又可得
,唯一性得证。
基金项目
国家自然科学基金资助项目(11561028,11801238),江西省教育厅青年科学基金资助项目(GJJ170566,GJJ170567,GJJ170525),江西理工大学大学生创新创业训练项目(DC2018-072),江西理工大学本科教学工程项目(XZG-16-01-05)。