基于FY-3D MERSI-2数据的干旱/半干旱地区地表温度反演

Land Surface Temperature Retrieval from FY-3D MERSI-2 Data in the Arid/Semi-Arid Area

摘要: 本文将一种改进的广义分裂窗算法(GSW)用于风云三号D星(FY-3D)中分辨率光谱成像仪II (MERSI-2)数据反演干旱/半干旱地区地表温度。通过MODTRAN5.2和大气廓线数数据TIGR2311 (Thermodynamic Initial Guess Retrieval database)进行辐射传输模拟建立时空代表性的模拟数据库，然后使用稳健回归方法建立不同热红外波段平均发射率(ε)，大气水汽含量(WVC)以及地表温度(LST)区间的GSW算法系数查找表。最后使用热带廓线、中纬度夏季廓线和实测的土壤样本波段发射率作为输入模拟得到2448个验证数据，对算法进行了精度验证。表明改进的GSW算法在干旱、半干旱地区，观测角度不大于30˚的时候，反演精度高。

Abstract: This paper uses an improved Generalized Split-Window (GSW) algorithm to retrieve the land surface temperature (LST) in the arid/semi-arid areas from the data acquired by Medium Resolution Spectral Imager II (MERSI-2) on FengYun 3D (FY-3D). The coefficients in the GSW algorithm corresponding to a series of ranges for the mean emissivity(ε), the atmospheric Water Vapor Content (WVC), and the land surface temperature LST are derived using a robust regression method from the space-time representative numerical values simulated with an accurate MODTRAN 5.2 and Thermodynamic Initial Guess Retrieval database (TIGR2311). At last, 2448 simulative validation data are obtained by MODTRAN5.2, using tropical profilers, mid-latitude summer profilers and band emissivity of measured soil samples as input parameters, to verify the accuracy of the algorithm. The results show that the improved GSW algorithm has high accuracy when the observation angle is not more than 30˚ in the arid and semi-arid areas.

1. 引言

地表温度(Land Surface Temperature, LST)是地表物理过程的关键参数，在地表与大气相互作用以及大气和陆地之间能量交换的过程中起着重要作用，准确获取地表温度对气象、水文、生态、全球变化等众多研究领域具有重要的意义 [1] [2] 。但地表温度是时空变化非常大的一个物理量，传统的地面站点观测难以满足其应用要求，因此使用卫星遥感数据在区域或全球范围内长时间的监测地表温度分布及其变化成为研究热点。为了获取更为准确的LST，研究者们提出了大量的算法。而主要的三类算法，分别是单波段算法 [3] [4] [5] [6] 、分裂窗算法(Split-window algorithm, SW) [7] [8] [9] [10] [11] 和温度与发射率分离算法(Temperature emissivity separation method, TES) [12] [13] [14] 。分裂窗算法是利用大气窗口10.5~12.5 μm内两个相邻波段(中心为~11 μm和~12 μm)的大气吸收特性不同(尤其对大气水汽)，通过对这两个波段亮温的某种组合来剔除大气影响。MODIS地表温度产品官方算法广义分裂窗算法(generalized split-window, GSW) [7] [15] 是分裂窗算法中用于产品业务化生产且验证较多的算法之一。

中分辨率光谱成像仪II (MERSI-2)为我国2017年11月发射的风云三号D星(FY-3D)上搭载的核心仪器之一，整合了原有风云三号卫星两台成像仪器(MERSI-1和VIRR)的功能，能够对大气、陆地、海洋进行连续综合观测，实现云特性、气溶胶、陆地表面特性、海洋水色、低层水汽等地球物理要素的高精度定量遥感反演 [16] [17] 。

MERSI-2红外波段由VIRR的3个红外窗口升级到5个(表1)，它是世界上首台能够获取全球250米分辨率红外分裂窗区资料的成像仪器。MERSI-2热红外分裂窗波段第24和25波段与MODIS分裂窗波段光谱响应对比图(图1)。从图中可以看出，两者响应函数存在一定区别，因此本文旨在分析用改进的GSW算法反演MERSI-2干旱/半干旱地区地表温度的精度。首先使用了MODTRAN5.2和大气廓线数数据TIGR2311 [18] 来进行辐射传输模拟，获得从MERSI-2数据中反演LST的广义分裂窗算法系数，然后使用模拟数据对算法精度进行验证。

Table 1. Technical parameters of MERSI-2 infrared band

表1. 红外波段技术参数

Figure 1. Spectral response functions between MERSI-2 and MODIS split-window bands

图1. MERSI-2与MODIS分裂窗波段光谱响应对比图

2. FY-3D MERSI-2干旱/半干旱地区地表温度反演

2.1. 改进的广义分裂窗算法介绍

广义分裂窗算法最早由Wan和Dozier提出用于MODIS陆面温度反演 [7] 。经过大量的验证发现，广义分裂窗算法使用MODIS数据获取的温热地区裸露地表(干旱/半干旱地区)的地表温度产存在较大误差。为此，Wan [13] 改进了广义分裂窗算法，改进后的算法专门用于反演干旱/半干旱区裸露地表温度。其公式如下：

$T_s=C+\left(A_1+A_2\frac{1-\epsilon }{\epsilon }+A_3\frac{\Delta \epsilon }{{\epsilon }^2}\right)\frac{T_i+T_j}{2}+\left(B_1+B_2\frac{1-\epsilon }{\epsilon }+B_3\frac{\Delta \epsilon }{{\epsilon }^2}\right)\frac{T_i-T_j}{2}\text{+}D{\left(T_i-T_j\right)}^2$ (1)

式中 $\epsilon =\left({\epsilon }_i+{\epsilon }_j\right)/2$ 为分裂窗波段i，j的平均发射率， $\Delta \epsilon ={\epsilon }_i-{\epsilon }_j$， $\Delta \epsilon$ 为波段i，j的发射率(LSE)之差，T_s为地表温度，T_i，T_j为波段i，j大气层顶的亮温。C，A₁，A₂，A₃，B₁，B₂，B₃，D为未知系数。为了提高MODIS地表温度产品反演精度，研究者对卫星观测角、发射率平均值、大气水汽含量(WVC)、大气气温分为了几个区间，得到了各区间相应的方程系数。当广义分裂窗算法用于没有大气气温产品的传感器 [19] [20] ，可用LST分区间代替了大气温度分区间。在MERSI-2，分别对应分辨率为250 m的波段24和波段25。

2.2. FY-3DMERSI-2GSW算法系数获取

GSW算法的未知系数分三步获取：1) 使用大气辐射传输模型MODTRAN建立晴空条件下的大气参数查找表，包括大气透过率 ${\tau }_{\lambda \theta }$，大气上行辐射 $L_{\lambda \theta }^{atm\uparrow }$、大气下行辐射 $L_{a\lambda }^{atm\downarrow }$，用于简易辐射传输公式，这三个大气参数用热红外辐射大气传输计算软件MODTRAN 5.2模拟得到；2) 快速计算波段辐亮度；3) 计算FY-3D/MERSI-2第波段24、25波段的大气层顶(TOA)亮温；4) 分区建立FY-3D/MERSI-2 GSW算法系数查找表。

本文建立大气参数查找表时使用MODTRAN 5.2和大气廓线数数据TIGR2311中的晴空廓线来进行辐射传输模拟，共874条大气廓线被挑选使用 [21] 。MERSI-2为宽幅相机，观测角大，所以模拟时观测角度设置跨度大，从0˚到69˚。本文使用MODTRAN模拟获取大气参数时，详细参数设置如表2：

Table 2. Parameter settings table for MODTRAN5.2 simulation

表2. 使用MODTRAN5.2模拟时的参数设置表

注：12个观测角度为0，10，20，30，40，50，56.05，59.84，62.84，65.27，67.29，69。

根据式2)，2-1/2/3/4，用MERSI-2热红外波段24，25的光谱响应函数对MODTRAN模拟光谱辐射量( $L_{\lambda \theta }^{atm\uparrow }$， $L_{a\lambda }^{atm\downarrow }$， ${\tau }_{\lambda \theta }$ )进行积分，获得24，25波段的上下行辐射，和透过率。将24，25波段的地表发射率，上下行辐射和透过率，以及地表温度带入式2)，即可得到相应波段的TOA总辐射。LST根据大气气温确定，对于冷空气状况即大气气温T_air < 280 K时，T_air − 16 K到T_air + 4 K，热空气条件下T_air > 280 K，T_air − 5 K到T_air + 29 K。间隔均为1 K，平均发射率e从0.89到1，间隔为0.01，发射差Δe从−0.037到0.027，间隔为0.005。最后由普朗克函数即可得到相应波段的亮温。

建立模拟数据库后，通过稳健多元线性回归法获取FY-3D/MERSI-2GSW算法的系数 [22] 。为提高拟合精度，使用分段线性来近似非线性，将WVC，LST，和e均分为几个子区间，为了防止解出现奇异值，相邻的两区间均设置重叠区。WVC从0到6.5 g/cm²分为6个区间，设置0.5 g/cm²的重叠区。LST分为5个子区间：<280 K，[275, 295]，[290, 310]，[305, 325]，and >320 K。e分为两个区间：[0.89, 0.96]，[0.94, 1]，间隔均为0.002。观测角度同模拟时设置角度。

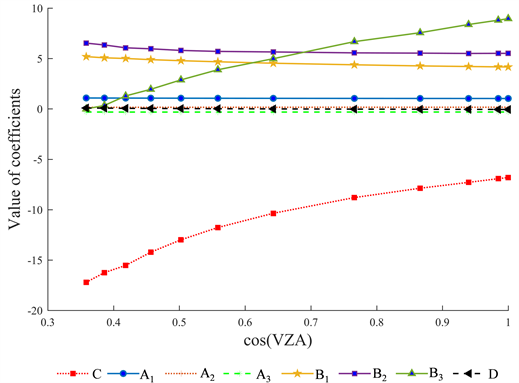
图2为WVC从1 g/cm²到2.5 g/cm²，LST从290 K到310 K时，两个地表发射率区间改进的FY-3D/ MERSI-2GSW算法系数与观测角余弦的关系图。从图中可以看出，GSW算法的系数与观测角度存在线性关系，相同的线性关系在其他区间同样存在，因此，模拟观测角之外的其他观测角度系数可以通过线性插值求的。

(a)

$\epsilon \in \left[0.89,0.96\right],\text{WVC}\in \left[1,2,5\right],\text{LST}\in \left[290,310\right]$

$\epsilon \in \left[0.94,1.00\right],\text{WVC}\in \left[1,2,5\right],\text{LST}\in \left[290,310\right]$

Figure 2. Examples of the GSW coefficients for FY-3D/MERSI-2 data

图2. FY-3D/MERSI-2GSW算法系数示例图

图3为12个观测角度下，不同WVC，ε以及LST区间使用GSW算法估算的温度与实际地表温度之间的均方根误差(RMSEs)。从图中可以发现：在所有区间LST区间，RMSEs随着观测角度和大气水汽含量的增大而增大。当观测角度大于60˚，RMSEs急剧增加。当VZA小于等于30˚，WVC小于4.5 g/cm²时，RMSEs小于1 K。那么在实际地表温度反演中，在数据充足的情况下，可以通过舍弃大角度观测值来提高反演精度。图3(f)为LST未分区情况下的RMSEs，可以看出未分区时RMSEs相对较大。由此可得，通过对LST分区，能在一定程度上提高LST反演的精度。

(a) LST < 280 K (b) 275 K < LST < 295 K (c) 290 K < LST < 310 K (d) 305 K < LST < 325 K (e) 320 K < LST (f) LST不分区间

Figure 3. Examples of RMSEs between the estimated and actual LST

图3. FY-3D/MERSI-2GSW系数拟合均方根误差示例

3. 验证分析

验证算法精度，可将该算法系数用于中国西北干旱/半干旱地区的地表温度反演，并与地表实测数据进行验证。但是由于目前缺少实测数据，本文先使用模拟数据对算法精度进行验证。

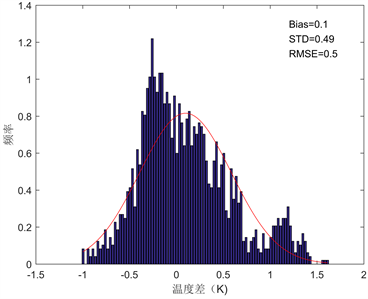
建立验证模拟库使用MODTRAN5.2自带的热带和中纬度夏季廓线，代表干旱地区大气状况。这两条廓线在模拟系数时并没有使用，用来模拟数据库验证合理。由于这两条大气廓线的大气气温都高于280 K，LST设置为T_air − 5 K到T_air + 20 K，间隔5 K，最终LST从289.2 K到319.7 K。观测角度为0˚，15˚, 30˚和69˚，利用MERSI-2第24，25波段响应函数和ASTER 2.0光谱库 [23] 土壤样本数据共51条，积分得到裸土的波段发射率作为输入。被选用的土壤样本波段平均发射率从0.96到0.98，波段发射率之差从−0.01到0.003。经过模拟共得到2448个24，25波段的大气层顶辐亮度，进而得到波段亮温。最后利用改进的GSW算法系数进行LST估算。计算时先不考虑地表温度分区，使用系数近似估计地表温度，然后根据近似地表温度，选择其所属地表温度区间的系数计算地表温度，多次迭代直到地表温度两次差值小于某阈值，这时所得到的温度即为精确地表温度。验证时计算偏差(Bias)、标准差(STD)以及均方根误差(Root-Mean-Square-Error, RMSE)。估算的地表温度与实际地表温度误差直方图见图4。

(a) 不包含69˚ VZA(b) 包含69˚ VZA

Figure 4. Error histogram of the estimated and actual LST

图4. 估算的地表温度与实际地表温度误差直方图

从图4(a)中可以看出，改进的广义分裂窗算法，在小角度观测状况下(VZA ≤ 30)，反演精度较高。Bias为0.1，STD为0.49，RMSE为0.5，地表温度反演精度能满足小于1 K的精度要求。但是在大角度观测下，算法误差较大。在VZA达到69˚时，误差最大接近8 K。这说明该算法在观测角度较大时精度有限，将在以后的工作中进行改进。

4. 总结

本文将一种改进的广义分裂窗算法用于风云三号D卫星(FY-3D)搭载的中分辨率光谱成像仪II (MERSI-2)数据反演干旱/半干旱地区的地表温度。通过MODTRAN5.2和大气廓线数数据TIGR2311进行模拟建立具有时空代表性的模拟数据库。为了提高算法反演精度，将热红外波段ε、WVC以及LST分为不同区间建立GSW算法系数查找表。然后使用热带廓线、中纬度夏季廓线和实测的土壤波段发射率作为输入建立模拟数据对算法进行了精度验证，表明GSW算法在干旱、半干旱地区，VZA观测角度不大于30˚的时候，反演精度高。其中Bias为0.1，STD为0.49，RMSE为0.5。为了进一步验证该算法的实际应用精度，接下来会将该系数用于中国西北干旱地区的MERSI-2数据地表温度反演，并通过地面实测数据对比验证其精度。