1. 前言
偏微分方程的应用涉略于多个领域,与许多学科中的交叉学科(比如:数学物理、金融数学、生物医学和通讯工程等)相互结合共同进步、共同发展。偏微分方程的重要源泉是物理学、力学、电磁学与几何学。它起源于18世纪,发展于19世纪,兴盛于20世纪至今,在信息通讯、工程技术、生物数学、金融数学和图像处理等领域中备受关注。首先介绍了偏微分方程的发展及其意义;其次,在20世纪末以来,偏微分方程在备受关注的生物医学、物理学、金融数学与图像处理等领域大量涌现并得到应用。比如有年龄结构SIS型的传染病、微分几何、证券投资与图像处理等模型;最后,通过已叙述的几个实例说明建立数学模型并在其中运用偏微分方程的重要性,它们极大地推动了科学、技术、工程技术和社会的进步与发展。同时,它们也无时无刻地环绕在我们的身边,为我们的生活的各个方面提供着极大的便利,影响着我们的生活。
2. 偏微分方程的发展及意义
2.1. 偏微分方程的发展
(一) 18世纪的偏微分方程
微积分学的深入发展和广泛应用是18世纪数学的主流,它刺激和推动了偏微分方程等许多新分支的产生。欧拉(Leonhard Euler,1707~1783,瑞士)在1734年提出了特殊的偏微分方程,即弦振动的二阶方程。他还引进了许多现代数学的术语和书写格式,最为著名的是第一个将函数表示为
。拉普拉斯(Pierre-Simon Laplace,1749~1827,法国)曾说:读读欧拉,他是我们所有人的老师(Read Euler,read Euler,he is the master of us all)。从科研成果来说,欧拉在数学史上甚至是自然科学史上首屈一指的数学家 [1]。他在创建数学纯粹理论的同时,还应用数学工具去解决大量的来自天文、物理和力学等方面的实际问题。
1743年,达朗贝尔(Jean-Baptiste le Rond d’Alembert,1717~1783,法国)在动力学的著作中提出了特殊的偏微分方程,却并未引起多大的关注。1747 年,在《张紧在弦振动时形成的曲线研究(Recherches sur la courbe que forme une corde tenduë mise en vibration)》中首先明确了弦振动方程
,
且给出了其通解的表达式
称为达朗贝尔解,引入分离变量思想为解偏微分方程提供了方法,故被看作偏微分方程论的发端 [2]。
1753年,数学家丹尼尔·贝努利(Daniel Bernoulli,1700~1782,瑞士)发表了《弦振动问题新思考》。他假定初始曲线都可以用正弦级数来表示,从而弦振动问题的解都可以表示为正弦周期模式的叠加。同时,他在数学物理方面的问题上提出了对于求解弹性系统在振动方面具有一般性的方法,这对于偏微分方程的发展有着很大的影响 [2]。
18世纪中另一类重要的偏微分方程,即位势方程(又称为拉普拉斯方程,调和方程),这与当时另一个热门的问题计算两个物体之间的引力是相关的。被誉为“法国牛顿”的拉普拉斯在1785年发表的论文《球状物体的引力理论与行星形状(Théorie du movement et de la figure elliptique des planètes)》中引进了标量函数V,推导出V所满足的方程
,
这就是位势方程,也称为拉普拉斯方程(Laplace方程) [3]。
(二) 19世纪的偏微分方程
在19世纪这一期间,数学家与物理学家关注的核心是偏微分方程,主要有两点原因:一是偏微分方程在物理学、力学、电磁学研究中的大量应用;二是促进了函数论、代数和无穷级数等分支的快速发展,极大地推动了数学的进步。
19世纪傅里叶(Joseph Fourier,1768~1830,法国)在偏微分方程求解方面迈出了至关重要的一步。1807年,他提交给巴黎科学院关于热传导方程
的论文,并在求解该方程时,发现了许多函数都可由三角函数构成的级数形式表示。1822年,他出版了《热的解析理论(Théorie analytique de la chaleur)》,他认为任意周期函数都可表示为正弦函数和余弦函数,同时也提出了变量分离法,在物理与近代数学方面都产生了深远的影响,是现今一部将数学理论应用于物理学的科学元典。热力学之父汤姆森(William Thomson,1st Baron Kelvin,1824~1907,英国)和泰特(Peter Guthrie Tait,1831~1901,英国)在《自然哲学(Treatise on Natural Philosophy)》中曾说:“傅里叶的定理不仅是现代分析学中最美妙的成果之一,而且是现代物理研究不可或缺的工具 [2]。”马克思主义的创始人之一、辩证唯物主义哲学家恩格斯(Friedrich Von Engels,1820~1895,德国)写道:傅里叶是一首数学的诗,黑格尔是一首辩证法的诗 [4]。傅里叶的思想和方法在很多方面潜移默化的影响着我们的生活。例如,拍摄数码照片时会自动地将拍摄到的图像进行压缩处理并存储在数码相机里,使用JPEG数据压缩方法的其中一个步骤就是傅里叶变换;语音识别中将复杂的信号波分解为许多单一频率分量中应用到傅里叶变换;核磁共振成像扫描中的脉冲函数序列、
函数和方波脉冲函数中也有应用到傅里叶变换。
在求解位势方程
方面,1828年,格林(George Green,1793~1841,英国)在《数学分析在电磁学理论中的应用的一篇论文(An essay on the application of mathematical analysis to the theories of electricity and magnetism)》中引入位势的概念,并将位势函数概念运用到电磁学中,是创立了电学和磁学的数学理论的第一人 [1]。他在求解位势方程解所应用到的方法称为奇异点方法。
1828年,仅次于欧拉的多产数学家柯西(Augustin Louis Cauchy,1789~1857,法国)等人得到了弹性介质方程组
1864年,麦克斯韦(James Clerk Maxwell,1831~1879,英国)在法拉第(Michael Faraday,1791~1867,英国)关于电磁实验的基础上提出了麦克斯韦方程组
这个方程就是偏微分方程组,此方程组反应了电磁学现象,将电学与磁学统一为电磁学,预言了电磁波的存在。该方程组是19世纪偏微分方程最重要的结果,被誉为“物理学的第二次大统一”,也被列入“改变世界面貌的10个公式”之一 [2]。
对于偏微分方程,柯西是第一个讨论偏微分方程解的存在性,他在讨论偏微分方程组解的存在性时提出了特征方法并给出了优函数方法进而证明解的存在性 [1]。
后来,柯瓦列夫斯卡娅(Sofia Kovalevskaya,1850~1891,俄国)独立地发展为包括拟线性方程和高阶方程组在内的非常一般的形式 [3]。有关偏微分方程解的存在唯一性定理被称为Cauchy-Kovalevskaya定理,其与常微分方程中
初值问题幂级数解的存在唯一性定理同等重要。
(三) 20世纪的偏微分方程
1900年,希尔伯特(David Hilbert,1862~1943,德国)提出了数学家今后需努力解决的“23个数学问题”,也被称为是20世纪数学的至高点,有力地推动了20世纪数学的发展。其中的第19、20和23个问题分别为“正则变分问题的解是否总是解析函数”、“研究一般边值问题”、“发展变分学方法的研究”,与偏微分方程息息有关,如今已发展成为一个很大的数学分支。
由于第二次世界大战的爆发,刚成立的美国普林斯顿高等研究所抓住了机遇,大量著名的欧洲数学家移民到了美国,包括希尔伯特的接班人外尔(Hermann Weyl,1885~1955,德国),创新数学大师冯·诺依曼(John von Neuman,1903~1957,匈牙利,美国),以及哥根廷大学数学系的主持人柯朗(Richard Courant,1888~1972,德国,美国)等,都汇集于普林斯顿高等研究所集中了众多世界一流的数学家到此工作 [2]。1943年,在西南联合大学任教的陈省身(Shiing-Shen Chern,1911~2004,国际数学大师)先生也被邀请前往普林斯顿高等研究所进行学术访问,并于1943年冬天在普林斯顿高等研究所完成Gauss-Bonnet公式的内蕴证明,现称为Gauss-Bonnet-Chern公式,是现代微分几何的奠基人,1984年荣获沃尔夫奖 [3]。
第二次世界大战使得美国政府想要将数学与科学技术、数学与军事目标密切地结合在一起,开辟了美国数学发展的新时代。于1942年成立了应用数学组,并与11所大学签订了合同,帮助解决战争中所遇到的数学问题。例如,在纽约大学,柯朗和弗里德里希斯(Kurt Otto Friedrichs,1901~1982,德国)领导的小组研究空气动力学、水下爆破和喷气火箭理论、超音速飞机带来的发展成为柯朗数学研究所 [5] ;在布朗大学,以普拉格(William Prager,1903~1980,德国,美国)为首的应用小组着重于研究经典动力学与畸变介质力学,目的是延长军备的使用时间 [5] ;在哈佛大学,伯克霍夫(Garrett Birkhoff,1911~1996,美国)主要研究雷达瞄准和弹道学等流体力学问题 [5]。
第二次世界大战之后,偏微分方程理论取得巨大的进步。20世纪50年代中期,菲尔兹奖和沃尔夫奖得主赫尔曼德尔 [3] (Lars Valter Hörmander,1931~2012,瑞典)、马尔格朗日(Bernard Malgrange,1928~,法国)与埃伦普里斯(Leon Ehrenpreis,1930~2010,美国)独立证明了常系数线性偏微分方程的可解性 [3]。但是,沃尔夫奖得主卢伊 [3] (Hans Lewy,1904~1988,美国)在1957年举出了一个反例
,
进而可以构造出实系数方程的反例。1973年,菲尔兹奖得主费弗曼 [3] (Charles Louis Fefferman,1949~,美国)给出了非退化线性偏微分方程局部可解性的一个充分必要条件。相比线性方程而言,非线性方程的研究却十分困难,进展缓慢。
1834年8月,造船工程师罗素(John Scott Russell,1808~1882,苏格兰)将在行驶中波形不随时间改变的水波包称为孤立波 [6],随后专门从事孤立波的研究,发表了论文《论水波(Report on waves)》。
1895年,科尔泰沃赫(Diederik Johannes Korteweg,1848~1941,荷兰)和德弗里斯(Gustav De Vries,1866~1934,荷兰)获得了描述孤立波现象数学模型 [6]
并给出了一个类似于罗素孤立波的解析解。此方程称为科尔泰沃赫-德弗里斯方程(Korteweg-de Vries Equation),简称KdV方程,但在其后60多年中停滞不前。
1960年,加德纳(Clifford Spear Gardner,1924~2013,美国)等人发展出了“散射反演方法”,且成功地求解了KdV方程 [6]。后来人们发现光纤通信、神经细胞脉冲传导、木星红斑活动等都存在孤立子性质。
(四) 偏微分方程在中国发展的历程
魏时珍(1895~1992)的研究领域是微分方程和数学物理,是最早向国内介绍爱因斯坦相对论的。1922年考入“数学王国”哥根廷大学,1925年以论文《在平均负荷下四边固定的矩阵平板所呈现的现象(Über die eingespan nte rechtechige Platte mit gleichma Big vertechige Belastung)》在德国获得应用数学博士学位的第一位中国人,导师是柯朗。1925年回国后在同济大学、四川大学等高校工作,积极教书育人 [7]。1936 年参考柯朗《偏微分方程讲义》的基础上,撰写了第一本中文的偏微分方程教材《偏微分方程式理论》。
1937年吴新谋(1910~1989)公费留学法国,先师从维拉(Henri Villat,1879~1972,法国),后面跟随阿达玛研究偏微分方程。1951年回国后,他在中科院研究所任研究员时建立了微分方程研究室。1954年在国内主持了第一个以现代偏微分方程理论为主题的大型暑期讲习班 [8]。1956 年他编写了新中国第一本偏微分方程教材《数学物理方程讲义》,之后又扩充为三卷本《数学物理方程》。1961年他主持召开了全国微分方程会议。他是中国偏微分方程研究事业的主要开创者之一。
蒋硕民,北京师范大学二级教授,研究方向为偏微分方程与近世代数。他的博士生导师原来是柯朗(Richard Courant,1888~1972,德国)。后改为雷利希指导。1935年他的博士论文《一个关于两个变量n阶偏微分方程的混合边值问题》获得通过,并应数学家姜立夫(1890~1978年,南开大学数学系创始人)先生之邀回国在南开大学数学系任教授,时年22岁。1954年调至北京师范大学。他是中国研究偏微分方程学科的先行者,近世代数的早期介绍者之一 [8]。
刚开始建立京师大学堂,数学在教学中占有很高的比例。1904年1月13日,我国以政府名义颁布了第一部完整的学制章程《钦定学堂章程》,其中算学门(即“数学系”)的课程就包含了部分微分方程式论(即偏微分方程)等。法国数学家阿达玛1936年来清华大学讲学3个多月,1964年在中国出版了《偏微分方程论》。1954年周毓麟(1923~ )被选派到莫斯科大学,师从女数学家奥列尼克(Olga Arsenievna Oleinik,1925~2001,苏联,俄罗斯),成为中华人民共和国成立之后第一个学习偏微分方程理论的留学生。建国初期偏微分方程领域的国际学术交流活动主要是请苏联和东欧专家前来访问和讲学 [8]。例如,1958年苏联科学院通讯院士比察捷(A.B. Bitsadze,1916~1994)到北京大学讲授混合型偏微分方程;在科学研究方面,周毓麟进行了与空气动力学有关的混合型偏微分方程、与毛细管现象有关的非线性椭圆型
和抛物型偏微分方程
的研究 [9]。1962年,全国讲师以上职称的偏微分方程工作者已达数百人。
2.2. 偏微分方程的研究意义
随着科学技术的发展,偏微分方程的研究领域得到了不断地扩大,尤其是应用科学的发展,已然成为连系数学理论和实际应用之间不可或缺的一条纽带。尤其是数学与其他学科中的交叉学科(如数学生物学、数学物理学、数学金融学和图像处理等)的快速发展,使得近年来国内外的偏微分方程实际应用非常多。一方面是人们不间断地提出有关偏微分方程的新问题,例如,近几年以来,在生物学、生态学、生命科学和众多工程技术领域建立了很多偏微分方程,其中包含了许多新形式的偏微分方程;另一方面,在偏微分方程研究的过程中提出了许多有关于新学科中的新方法,例如,泛函分析中算子半群方法、广义函数法、数值分析中有限元法(即Ritz-Galerkin法)等作为处理线性和非线性偏微分方程问题提供了强有力的框架和工具,遥感和图像处理中的多种模型和反问题,在实际中得到了广泛的应用 [10]。
我们知道偏微分方程不仅是方程理论性与应用性并举的一门学科,更是解决数学问题与生活问题的一种重要的工具。我们熟知偏微分方程起源于18世纪,发展于19世纪,丰富于20世纪。如果没有偏微分方程的存在,人类现有的大部分技术可能都无法被发明出来(例如,人们日常生活中常用手机中的语音通话功能运用到傅里叶变换及其逆变换);如果没有偏微分方程的存在,人类可能还处于中世纪的生活(例如,人们所居住房屋中的梁顶满足横向振动的偏微分方程:
);如果没有偏微分方程中方程式的存在,我们不可能明白冲刷海滩的波涛(例如,描述水波运动的弱非线性弱色散性的近似水波方程为:
和
)、以及变化莫测的天气(例如,大尺度干大气的三维粘性的简化方程组为
)等现象的物理学原理;如果没有偏微分方程的存在,我们不可能清楚了解宇宙的广袤,甚至是我们在宇宙中所处的位置。所以,我们可以知道偏微分方程的应用是极其广泛的,它无时无刻地环绕在我们的身边,为我们的生活的各个方面提供着极大的便利,影响着我们的生活。
3. 数学模型应用问题
偏微分方程的重要源泉是物理学、力学、电磁学与几何学。20世纪末以来,偏微分方程在备受关注的生物医学、物理学、金融数学与图像处理等领域大量涌现。这里首先介绍了年龄结构SIS型的传染病模型,其次是物理学中KdV方程流体模型,最后是微分几何、证券投资与图像处理中的应用模型。
3.1. 年龄结构的SIS型传染病模型
运用数学方法去研究传染病的发病机理、动态过程以及发展趋势,已经为现在一个比较活跃的研究领域。很多传染病的传播都与年龄有关,因此,建立年龄结构的传染病模型具有重要意义。下面建立传染病动力学的偏微分方程模型。
将人口种群分为两种,一种是正常易受感染者;另一种为患病者。第一种人因受感染而变成第二种人,而第二种人因治愈而重新变回为第一种人。并且这两种人都存在自然死亡。其中我们记
为自然死亡率,
为感染率,
为康复率。
设
表示第一种人在时刻t按年龄x的分布密度函数,
表示第二种人在时刻t按年龄x的分布密度函数,于是在时刻t,年龄在区间
中的第一种人数为
,年龄在区间
中的第二种人数为
。
表示在时刻
,年龄在区间
中的第一种人数,即其对应的人数是第一种人在时刻t,年龄区间
在其任意小的一个
区间的人数
减去在该时段的自然死亡的人数
,再减去第一种人因受感染而成为第二种人的人数
,最后还需加上第二种人被治愈康复成为第一种人的人数
,即
则有
类似于人口方程的推导,得
同理,
表示在时刻t + dt,年龄在区间
中的第二种人数,即其对应的人数是第二种人在时刻t年龄区间
在其任意小的一个dt区间人数
减去在该时段的自然死亡的人数
,再减去第二种人被治愈康复成为第一种人的人数
,最后还需加上第一种人因受感染而成为第二种人的人数
,即
则有
因此有
又有初始条件:
,
和边界条件:
,
所以可得,年龄结构的SIS型的传染病模型为
3.2. KdV方程流体模型
由流体力学知,在重力的作用下,不可压缩无粘流体的运动满足连续方程
(1)
和动量方程
(2)
其中 是流速,
是流速, 是重力加速度,
是重力加速度, 是梯度算子,
是梯度算子, 是密度(常数),p是压强。
是密度(常数),p是压强。
选取适当的空间坐标系,使得重力加速度向量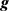 指向z坐标轴的负方向。当
指向z坐标轴的负方向。当 满足
满足 ,即
,即 的旋度为零向量时,流动称为是无旋的。对单连通区域,无旋的流动一定存在一势函数
的旋度为零向量时,流动称为是无旋的。对单连通区域,无旋的流动一定存在一势函数 (在多连通区域时有多值函数),使得满足
(在多连通区域时有多值函数),使得满足
 , (3)
, (3)
此时有
 ,
,
从而动量方程(2)式通过积分可化为
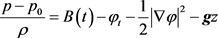 ,
,
其中 分别是由积分产生的积分常数和只依赖于t的函数,
分别是由积分产生的积分常数和只依赖于t的函数, 为某一处的压强。若用
为某一处的压强。若用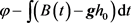 代替
代替 ,则(2)式不受影响,从而上式可化简为
,则(2)式不受影响,从而上式可化简为
 (4)
(4)
其中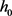 是一个任意常数,可取为某个基准高度。由连续方程(1)式和(3)式得到
是一个任意常数,可取为某个基准高度。由连续方程(1)式和(3)式得到
 , (5)
, (5)
其中 为Laplace算子,(5)式为Laplace方程。若此方程依赖于t的解
为Laplace算子,(5)式为Laplace方程。若此方程依赖于t的解 ,
,
从(4)式就可以得出速度 ,此时动量方程(2)式也就满足了。
,此时动量方程(2)式也就满足了。
若假设流体在具有固壁的容器中运动,而流体表面是和空气接触的。设流体表面的方程为
 , (6)
, (6)
若设 表示流体表面上一条流线的方程,沿此流线流速向量
表示流体表面上一条流线的方程,沿此流线流速向量 的分量为
的分量为

对流线上任意点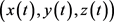 ,则有
,则有
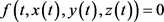 ,
,
关于t求导得
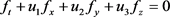
这是流体表面上的一个边界条件。特别地,当流体表面方程可表为显性方程
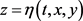 ,
,
则在此表面上的上述边界条件可写为
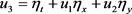 , (7)
, (7)
流体表面上的压强应和大气的压强相等,设为 ,则有(4)式得出流体表面上另一边界条件
,则有(4)式得出流体表面上另一边界条件
 (8)
(8)
流体表面形状事先未定, 为未知函数,因此
为未知函数,因此 也是一个自由边界。此外,在容器固壁处的边界条件是
也是一个自由边界。此外,在容器固壁处的边界条件是

即在固壁处流动的法向速度为零。
从而有流体在固壁的容器中流动的边值问题
 (9)
(9)
进一步考虑流体在水槽(或河道)中的运动。设底部是水平的固壁,即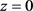 ,对应的边界条件是
,对应的边界条件是 。假设流动状态只和坐标
。假设流动状态只和坐标 有关,其在y方向的流速为零,将波的表面记为
有关,其在y方向的流速为零,将波的表面记为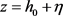 ,其中
,其中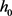 为表面的基准高度。l表示波长,
为表面的基准高度。l表示波长, 表示近似的波速,重选自变量和未知函数的单位,令
表示近似的波速,重选自变量和未知函数的单位,令
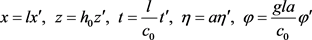 ,
,
其中a是表示表面波的波幅大小的常数。此时方程(5)式和边界条件 ,(7)式和(8)式可化为
,(7)式和(8)式可化为
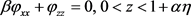 ,
,
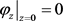 ,
,
 ,
,
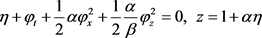 . (10)
. (10)
其中 。由此可知,当
。由此可知,当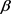 取小值时表示波长较长,当a取小值时表示波幅较小。求(10)式的
取小值时表示波长较长,当a取小值时表示波幅较小。求(10)式的
通解并代入边界条件,同时在长波长和小振幅的假设下忽略含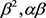 的项,可知
的项,可知
 ,
,
再作变换
 ,
, 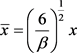 ,
,  ,
,
且将 仍记作
仍记作 ,则可得到KdV方程 [10] [11]
,则可得到KdV方程 [10] [11]
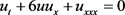 .
.
3.3. 极小曲面方程
极小曲面问题最早是由物理学家普拉托(Joseph Antoine Ferdinand Plateau,1801~1883,比利时)通过“肥皂泡现象”而提出,又被称为普拉托问题。1840年,普拉托关于最小表面积问题的基础上进行了实验研究。通过在做实验的过程中偶然发现,一位仆人不小心将油溅入盛有混合水和酒精的容器里,从而他注意到此时所呈现出的球形。随后,普拉托改用肥皂溶液和甘油进行实验,并把蘸湿的线框放入其中,得到了结果。正如我们现在的生活中小时候的吹泡泡游戏,把一个带柄的塑料环浸入肥皂水中,然后轻轻的取出,在塑料环上就会形成一个处于平衡状态的彩色薄膜,见图1。

Figure 1. A colorful film in a soap bubble
图1. 肥皂泡中的彩色薄膜
若忽略混合液体自身的重量、风力等外部因素,则薄膜的势能在表面张力的作用下会达到最小值,肥皂膜呈现出的曲面形状就是具有相对小的面积,即局部极小。对于极小曲面的研究,一般认为是“最伟大的数学家”拉格朗日(Joseph Lagrange,1763~1813,法国籍意大利裔)从1760年开始的,他第一次给出了这类曲面所应满足的偏微分方程。
在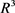 中考虑曲面
中考虑曲面
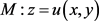 ,
,  ,
,
D是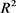 中的某一区域。拉格朗日利用变分法原理得出结论:在所有定义在区域D上且在其边界
中的某一区域。拉格朗日利用变分法原理得出结论:在所有定义在区域D上且在其边界 上取同样值的函数图像中,若存在曲面M的面积是局部极小的曲面,则u满足极小曲面方程
上取同样值的函数图像中,若存在曲面M的面积是局部极小的曲面,则u满足极小曲面方程
 ,
, 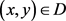 , (11)
, (11)
记M的变形
 ,
, 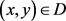 ,
,
其中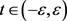 ,
, 为一个正常数,
为一个正常数,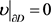 ,则
,则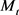 的面积
的面积
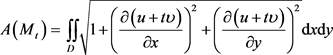
由 的局部极小性可知,
的局部极小性可知, 作为t的函数
作为t的函数 处取极小值
处取极小值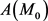 从而
从而
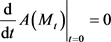 ,
,
即
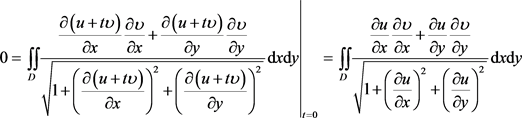
又由散度定理,并注意到 ,记
,记 是
是 的单位外法向量,可得
的单位外法向量,可得
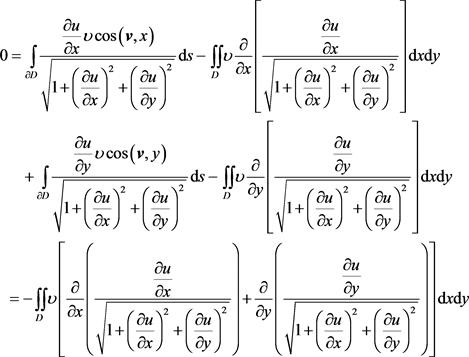
由 的任意性,在D中有
的任意性,在D中有
 ,
,
由此得到方程(11)式。极小曲面方程是二阶拟线性方程的代表,其中这里用到的极小曲面是局部极小的。
3.4. 布莱克–舒尔斯–默顿方程(BSM方程)
金融数学是近年来蓬勃发展的新兴学科,在金融界和数学界受到极大地关注度。它是运用数学工具建立合理的数学模型,进而对所建立的模型作进一步的分析、计算,目的是为了找出金融学中的相关规律,从而更好地运用于实践。金融数学可分为三类,分别为投资组合理论、衍生品定价理论和风险管理理论。其中在衍生品定价理论中的BSM方程最为出名。衍生品的定价理论起源于数学家布莱克(Fischer Sheffey Black,1938~1995,美国)、金融学家舒尔斯(Myron Scholes,1941~ ,美国)和默顿(Robert Cox Merton,1944~ ,美国)1973 年所开启的无套利定价理论,其核心是构造了一个定价测度。可以证明,一旦有了这个定价测度,衍生产品现时的价格就是其(经折现后的)到期价格的期望值。
以股票期权为例。设 为t时刻的股票价格,T为期权的到期日,r为市场的短期利率,
为t时刻的股票价格,T为期权的到期日,r为市场的短期利率,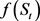 为到期日的合约价格函数,则t时刻的期权价格(即期权金)由下式给出:
为到期日的合约价格函数,则t时刻的期权价格(即期权金)由下式给出:
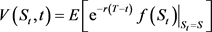 ,
,
其中S是t时刻的股票价格, 是条件数学期望。“对冲”是定价理论的一个重要概念,指特意减少另一项投资的风险的投资。通过支付期权金,投资人将风险转移给庄家,而庄家则通常要为期权卖出作对冲。标准的做法是买入或卖出一定数量的股票,而这个数量正是期权价格相对于股票价格的变化率
是条件数学期望。“对冲”是定价理论的一个重要概念,指特意减少另一项投资的风险的投资。通过支付期权金,投资人将风险转移给庄家,而庄家则通常要为期权卖出作对冲。标准的做法是买入或卖出一定数量的股票,而这个数量正是期权价格相对于股票价格的变化率

假设在股票价格的变化下需满足:
(1) 证券价格服从几何布朗运动,即 和
和 为常数;
为常数;
(2) 允许卖空标的证券;
(3) 没有交易费用和税收,所有证券是全部可分的;
(4) 衍生证券有效期内标的证券没有现金收益支付;
(5) 不存在无风险套利机会;
(6) 证券交易是连续的,价格变动也是连续的;
(7) 衍生证券有效期内,无风险利率r为常数。
由于假设股票价格S遵循几何布朗运动,所以有:
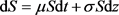 ,
,
在一个小的时间间隔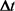 中,S的变化值
中,S的变化值 为:
为:
 ,
,
设V是依赖于S的衍生证券的价格,则V一定是S和t的函数,由伊藤引理(Ito’s Lemma)可知,
 ,
,
在一个小的时间间隔 中,V的变化值
中,V的变化值 满足:
满足:
 ,
,
为了消除风险源 ,可构建一个包括一单位衍生证券空头和
,可构建一个包括一单位衍生证券空头和 单位标的证券多头的组合。令
单位标的证券多头的组合。令 表
表
示为投资组合的价值,则有
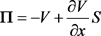 ,
,
在一个小的时间间隔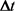 后,投资组合的价值V的变化值
后,投资组合的价值V的变化值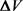 满足:
满足:
 ,
,
将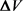 和
和 代入,可得
代入,可得
 ,
,
又由于消除了风险,组合 需获得无风险收益
需获得无风险收益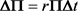 ,所以有
,所以有
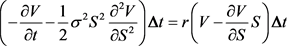 ,
,
化简整理可得,
 ,
,
此方程为BSM微分方程,其适用于其价格取决于标的证券价格S的所有衍生证券的定价。
又由于欧式看涨期权的价格c等于此期望值按无风险利率进行贴现后的现值,即
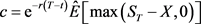 ,
,
其中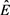 表示为风险中性条件下的期望值,和
表示为风险中性条件下的期望值,和
 ,
,
再令
 ,
,
其中
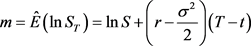 ,
,
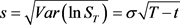 ,
,
可知,有
 ,
,
所以,随机变量W的密度函数 为:
为:
 ,
,
从而可有,
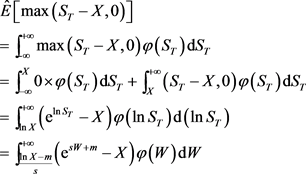

所以,可得
 ,
,
其中

和

从上面可看出,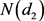 是风险中性世界中W大于
是风险中性世界中W大于 的概率,即风险中性世界中
的概率,即风险中性世界中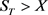 的概率。
的概率。
所以证明了 满足偏微分方程终值问题:
满足偏微分方程终值问题:

其中 为股价的波动率。该方程在定价方面存在一定的偏差,但仍是至今为止解决期权价格动态的最佳模型之一,应用十分广泛。
为股价的波动率。该方程在定价方面存在一定的偏差,但仍是至今为止解决期权价格动态的最佳模型之一,应用十分广泛。
3.5. AMSS (Affine Morphological Scale Space仿射形态尺度空间)方程
将偏微分方程引入图像处理领域中的一个研究方向是图像滤波。作为一个预处理手段,图像滤波几乎成为所有图像处理方法的前奏。早在1984年,Koenderink就发现了图像信号经过高斯滤波后的结果与热传导方程存在一定的联系。在许多场合图像滤波作为图像识别的一种预处理手段,它需要满足两个限制条件:对比度不变和仿射不变。而仿射不变性可以被分解为平移不变、旋转不变、欧氏不变、伸缩不变等。满足相关不变性条件的滤波器都有相对应的一族偏微分方程,随着逐渐对图像变换不变性要求的加强,可以选择的图像变换范围也在逐渐缩小,相应的可供选择的偏微分方程范围也在逐渐的缩小,最后只剩AMSS方程初值问题的解作为图像变换满足仿射不变性和对比不变性。
设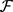 是图像函数空间,
是图像函数空间,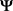 是
是 中所有水平集的集合。设对比变化下是稳定的,并且包含了T中所有元素的特征函数。令
中所有水平集的集合。设对比变化下是稳定的,并且包含了T中所有元素的特征函数。令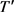 是T的伴随集合算子。如果对
是T的伴随集合算子。如果对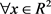 ,集合族
,集合族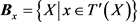 ,那么
,那么 有:
有:

对x几乎处处成立。其中 。
。
另外,如果T是位移不变算子,则
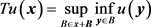
反之,若有一算子可表示成上式,则该算子是单调和对比不变的。
所以,若T是仿射不变的形态学算子,则必定是平移不变的形态学算子。通过上面的叙述可知,任意一个平移不变的形态学算子T都具有
 (12)
(12)
的表现形式。通过给(12)式加上一个局部化参数 ,构造出
,构造出
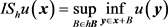 (13)
(13)
其中 。
。
如果:(i) 与任何满足
与任何满足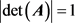 的矩阵
的矩阵 是可以交换的,
是可以交换的,
(ii) 常数c,
常数c, 满足
满足
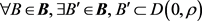
和

又假设图像函数u在x的某个邻域内是 的,且
的,且 时,
时,
 (14)
(14)
其中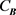 是一个仅仅与
是一个仅仅与 有关的常数。即,仿射不变形态学算子的微分特性 [12]。其中(ii)限制的条件是为了使
有关的常数。即,仿射不变形态学算子的微分特性 [12]。其中(ii)限制的条件是为了使 满足局部化条件。否则,无论h取多么小的值,
满足局部化条件。否则,无论h取多么小的值, 的取值不仅仅依赖于x某个邻域内的图像灰度值。
的取值不仅仅依赖于x某个邻域内的图像灰度值。
与线性滤波器和热传导方程中的方法类似,如果知道一个图像变换的微分性质后,可以通过局部化和迭代的方法导出相关的偏微分方程。令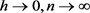 ,且
,且 ,令
,令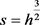 ,则有
,则有
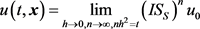
是偏微分方程
 (15)
(15)
初值问题在t时刻的解。在零时刻的初始值为原始图像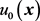 ,此时(15)式所表示的方程被称为AMSS方程。该方程在t时刻的解可以作为对图像
,此时(15)式所表示的方程被称为AMSS方程。该方程在t时刻的解可以作为对图像 滤波的结果,近似地用
滤波的结果,近似地用
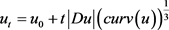
表示。这个滤波器通常被称为AMSS算子 [13]。该算子满足了平移不变、灰度平移不变、仿射不变、对比不变和数学形态等多种不变性,作为最好的一类滤波器可用于图像处理中以满足多种需求的光滑性。通过图像经过AMSS算子作用后在不同时刻的解可知,虽图像质量在 比较大的时候出现了退化,但它还是比较好的保留了边缘的信息,见图2。
比较大的时候出现了退化,但它还是比较好的保留了边缘的信息,见图2。
 (a) 肥皂泡中的彩色薄膜
(a) 肥皂泡中的彩色薄膜  (b) 部分水平集的叠加
(b) 部分水平集的叠加  (c) AMSS滤波器t = 0.4作用结果
(c) AMSS滤波器t = 0.4作用结果  (d) AMSS滤波器t = 2.0作用结果
(d) AMSS滤波器t = 2.0作用结果
Figure 2. The effect of the AMSS filter
图2. AMSS滤波器作用效果
若变换 满足 [14] 中的条件,则
满足 [14] 中的条件,则 是下列方程在t时刻的解:
是下列方程在t时刻的解:

其中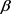 是连续的非减函数:
是连续的非减函数:
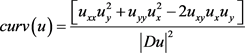
该式表示u的曲率,其中u表示为图像的亮度值。
在二维情况下,可以得知用于图像处理的简便形式的方程:
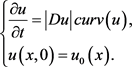 (16)
(16)
或
 (17)
(17)
称(16)式为MCM (Mean Curvature Motion)中值曲率驱动)方程,(17)式就是AMSS方程。用(17)式在t时刻的解作为滤波后的图像进行数字图像处理 [12],其具有独特的性能:可不依靠图像在三维空间中位置和方向的条件下,对平面形状进行细致的分析。因此,它是在基于微分方程的图像处理中举足轻重的地位,不仅能够很好地去除偏微分方程中的噪声,也能很好地保留图像的边缘信息,它是最具典型性的代表。例如:法国宇航局已采用AMSS算子作为对航拍图像进行图像增强的标准方法 [15]。通过利用偏微分方程去对于图像进行相关的处理就是利用偏微分方程把图像变形,然后求解出该方程进而获得图形处理的预期效果。偏微分方程在图像分割、图像重建、图像检索、对比度增强和医学图像处理等相关的图像处理方面都取得了很好的效果。
4. 数学模型的重要性
通过以上生活中不同方面数学模型的建立,可知道利用偏微分方程中的知识来建立数学模型在我们的实际生活中的应用是十分广泛的。合理而又正确地建立数学模型,在促进数学学科多方面发展的同时,也促进了社会的进步与发展。运用数学的语言与方法对各种实际对象作出抽象或模仿而形成的一种数学结构就是数学模型。它是数学中运用最典型的方法之一。其中把建立数学模型的过程称为数学建模。偏微分方程建模就是运用偏微分方程的思想和方法,去认真地了解、分析和解决社会中的应用问题。
数学模型这一方法越来越受到人们的重视,使许多的社会、经济等问题也越来越多的用偏微分方程(组)来建立,进而引起了社会各界的高度重视。我们要将实际问题转化为数学问题,构造出相应数学模型,从定性和定量的角度去分析和解决实际问题。例如,上面提到的BSM方程,不正是利用数学的工具,进行数学建模、理论分析等定量分析来研究金融方面的问题吗?回答当然是肯定的,正是利用与之相应的偏微分方程模型去代替生活中的实际对象,才可以将所需研究的现实问题运用数学模型表达成数学问题,再合理地利用数学工具去分析和处理问题,这样才能充分发挥数学工具在解决问题时的关键性作用,从而使我们能够深化对所需研究的实际问题的认识。
上述的几个用数学模型建立的偏微分方程的例子,目的就是为了说明建立数学模型具有重大的意义。现今科技与数学的飞速发展,以及电子计算机的广泛使用,使得想要实现数学化,建立数学模型成为了科技数学化的关键。我们身处于这个社会环境,经济发展等方面都需要运用数学模型,由于时间、空间的复杂性,需要忽略次要因素,抓住主要因素,建立合理、优化的偏微分方程模型,是为了让人们能更好、更方便地获取所需信息,从而推动社会的进步与发展。一些自然科学学科是比较容易建立偏微分方程模型的,如力学、物理学等,但也存在一些学科不是很容易建立偏微分方程模型,如生物学、金融学和社会学等。由于数学自身的快速发展,现代数学逐步地向高维、高次、多变量方向的迅猛发展,对于偏微分方程模型的建立要求也越来越高,不仅在于自然科学、工程建设等领域,更有经济、管理等领域,并成为一种解决社会环境,经济发展等问题的强有效的数学方法。
基金项目
获得2018年新疆维吾尔自治区研究生教育创新计划项目资助。
NOTES
*通讯作者。