1. 引言
复杂网络是由数据庞大的节点及节点之间错综复杂的关系所构成的网络结构。复杂网络普遍存在于现实生活中,如社会关系网络 [1] ,交通运输网络,基因网络等。因此,对复杂网络的研究成为近年来的热点问题 [2] 。
本文基于高斯图 [3] 模型(Gaussian Graphical Model, GGM)对复杂网络结构进行研究。其数学模型如下,假设
服从p维正态分布
,
为均值,
为协方差矩阵。利用
的样本
估计
[3] 。当
时,表示
与
条件独立。高斯图模型中,随机向量用无向图表示
[4] 。其中,V代表节点,每个节点分别对应随机向量的一个分量。
代表边,两个节点之间无边,当且仅当这两个节点对应的随机变量条件独立,即
。因此,判断协方差矩阵的逆
中的每个元素是否为0即是判断网络的结构。
在高斯图模型中,标准的模型选择方法是Greedy stepwise。该方法下参数估计结果是基于被选择的模型 [5] 。在每一步中,边的选择或删除通常通过在某个水平
的假设检验来完成。这种方法的缺点是没有正确地考虑到多重比较。另一个缺点是该方法在计算上具有复杂性 [5] 。为了解决以上问题,Drton和Perlman [6] 提出产生保守同步的
置信区间,并在每一步中利用这些置信区间进行模型选择。该方法的提出是基于对渐近性的考虑。Meinshausen和Buhlman [7] 为协方差选择提出具有较强计算能力的方法,可用于更庞大的高斯图。该方法为图中的每个节点进行领域选择,并结合选择结果来研究高斯浓度图模型的结构。Meinshausen和Buhlman说明了他们的方法对于稀疏高维图模型具有一致性。上述的这些方法,在模型选择和参数估计上都是分开的。并且,参数的估计是基于被选择的模型。Breiman [8] 也证明了这些方法在估计上具有不稳定性,即数据发生小的变动时,会导致估计结果有很大的不同。
本文提出的正则化模型在高斯图中可同时进行模型选择和参数估计,并使得估计结果具有稀疏性。正则子为The seamless-L0 (SEL0) [9] 。该正则化模型对所要估计矩阵非对角线上的元素进行SEL0惩罚。该思想类似于SEL0惩罚在线性回归模型中的应用。本文使用MM算法和Maxdet算法求解该模型。最后,通过数值模拟和实例分析说明本文提出的正则化模型有良好的模型选择和参数估计效果。
2. 正则化模型
设
服从p维正态分布
,
为均值,
为协方差矩阵。设
为协方差矩阵的逆。基于随机变量
样本观测值
的对数似然函数是
(1)
当不依赖于常数A和
时,设
的最大似然估计为
。其中
通常利用样本协方差矩阵
进行协方差矩阵的估计。因此,
可利用
或者
进行估计。但是,当变量的维数很大时,矩阵
稳定性差。并且,当
时,矩阵
是正定矩阵,矩阵中的元素不包含零项。所以,以此方法进行的估计结果是不具有稀疏性的图模型。
因此,通过引入L1正则子进行模型选择和参数估计。本文选择的L1正则子为SEL0惩罚,改惩罚形式是对L0惩罚的形式的模仿 [10] 。
但当变量维数很大时,该方法在计算上具有复杂性,并且具有不连续性和复杂性 [9] 。为解决上述问题,Dicker L.和Huang B.等提出SEL0惩罚。该惩罚形式为
(2)
其中,
是调节参数,当
很小时,
,并且,当
时,该方法呈现更好的效果。
因此,为了得到具备稀疏性的图模型结构,并更加准确的估计
。本文结合The seamless-L0惩罚(SEL0)和
寻找
的最大值。即
st
(3)
其中,
是调节参数。
因为对观测值作中心化处理。所以
。因此,(1)式可写为
st
(4)
进一步地,我们可以将(2)式写为
st
(5)
由于(3)式中的目标函数和可行区域都是凸的,因此,可以利用拉赫朗日形式将(3)式等价得写为
(6)
因此,最大化(4)式中的
,即可得到图模型的协方差矩阵的逆的估计。
3. Maxdet算法与参数选择
本文利用Maxdet算法 [11] 求解目标函数(6)。但由于本文中目标函数
的SEL0惩罚项是
和
惩罚函数的复合形式,因此,目标函数较难直接进行优化,需要利用Minorize-Maximization (MM) [12] 算法,构造
的Minorization函数
,其中,
是MM算法的第n部估计,也是参数a的一个定值。该函数逼近于原目标函数
且易于优化。因此,本节先构造出函数
,再通过对函数
利用Maxdet算法,得到逼近于
的估计值。最后使用BIC方法进行参数估计。
首先构造
的Minorization函数
。
若满足以下条件,则目标函数
可用构造函数
代替。
由于当
,
故
不等式两边同时加上
得
令不等式右边为
,即
(7)
故
,条件
满足。
又因
即
故
,条件
满足。
因此,
,且
故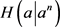 满足
,
两个条件。所以
的Minorization函数为
。
满足
,
两个条件。所以
的Minorization函数为
。
下面利用Maxdet算法求解式(7)。Maxdet问题的形式如下:
故对(7)式取负号,将其转化为求最小值问题。假设
的符号是已知的,设为
。根据Maxdet问题的形式,可将转化后的(5)式写成如下形式:
(8)
其中,
为第
项为1,其余项为0的
的矩阵,
为第
项为1,其余项为0的
的矩阵。
关于参数
的选择,常用的方法是多重交叉验证法,但计算上更有效的替代方案是用于模型选择和估计的BIC准则。因此,本文选择如下BIC准则选择参数
[13] :
其中,如果
,则
;其余情
。
下面式算法的具体步骤:
第一步:令
并且对任意的
,
。
第二步:令
在正定矩阵集上解决(6)式。
第三步:如果
,停止迭代并令
。否则,对所有的
设
,并且
,所以
。然后返回第二步。
第四步:使用BIC准则选择
,并输出相应的A的估计值。
4. 数值模拟
本文中的网络图模型由R语言huge包中的huge.generator函数生成,所生成的图形模式为随机模型。并且在此函数的输出结果中可得到该图形模式下随机生成的样本数据及其协方差矩阵。本文设置样本量为n = 200,维数p分别为15,30,50,100。分别比较本文提出的方法和Meinshausen & Buhlmann (mb)提出的方法在不同维数下参数估计和模型选择的情况。用KL损失量以及FPR (false positive rate),TPR (true positive rate)作为评价正则化模型在参数估计和模型选择上优良性的标准。其中,KL损失量(KL loss)为 [14] :
FPR和TPR为:
;
。其中,TPR越大,FPR越小说明模拟效果越好。
模拟结果如下(表1~表4)。
模型选择的目标是在高维数据中挑选出更具代表性的变量。表数据结果表明,在不同维数下,SEL0方法相比于mb方法在模型选择和参数估计方面均是最优的。并且在p = 15时,SEL0方法下所得到的KL loss最小,FPR达到最小,TPR达到最大。随着维数的增加,虽然KL loss值和FPR值逐渐增大,TPR值逐渐减小,但总体来说,gSEL0方法仍有较好的模型选择和参数估计能力。故综合以上结果,本文提出的gSEL0方法有良好的模型选择和参数估计能力。
5. 实例分析
本文将提出的正则化模型应用到基因调控网络的数据中。数据来源于Faith等人的论文数据 [15] 。该数据包含两个对象。第一个对象是40行,153列的矩阵,该矩阵的行和列代表了Escherichaia coil (E. coil)细菌在40种不同实验下,153种基因的基因表达水平,基因表达的测量结果指示了153种基因在每个特定的实验干扰下的活动水平。该153种基因是转录因子,在基因调控关系中有重要作用。第二个对象是一个邻接矩阵,概括了生物学文献中发现的E. coil细菌的153种基因之间已经实际存在的调控关系。结果如图1所示。
下面通过统计软件,首先根据邻接矩阵统计出生物学文献中已经发现的153种基因之间实际存在的调控关系的个数;然后利用本文提出的正则化模型,统计出在该模型下得到的生物学文献中已发现的实际调控关系及生物学文献中未被发现的调控关系的总量。步骤和结果如下:
1) 对邻接矩阵中基因之间的实际调控关系的个数进行统计,所得结果如下:
## IGRAPH UN-153 209
## attr: name (v/c)
结果表明:生物学文献中已经发现的基因之间的实际调控关系共209对。
2) 利用第一个数据对象中40行,153列的矩阵,根据本文提出的正则化模型,统计出在该模型下得到的生物学文献中已发现的实际调控关系及生物学文献中未被发现的调控关系的总量。所得结果如下:

Figure 1. Actual regulatory relationships among 153 genes
图1. 153个基因之间实际存在的调控关系
IGRAPH 68d9b0b U-153 554--
结果表明:根据本文提出的正则化模型共找到554对调控关系。
3) 最后统计在步骤2中利用本文提出的正则化模型得到的生物学文献中已发现的实际调控关系的个数。所得结果如下:
## IGRAPH UN-153 192--
结果表明:通过本文提出的正则化模型在已发现的209对实际调控关系中共得到了192对调控关系。这一结果进一步说明了该正则化模型在实际应用中的优良性。
6. 结论
本文基于高斯图模型进行复杂网络结构的研究,根据SEL0惩罚在线性回归模型中应用的思想,将其应用到图模型的模型选择和参数估计中,提出了新的正则化模型。本文使用Minorize-Maximization (MM)算法和Madex算法求解该模型。数值模拟实验结果显示,本文提出的正则化模型相比于Meinshausen & Buhlmann (mb)方法,KL loss值和FPR值更小,TPR值更大。说明本文提出的正则化模型在参数估计和模型选择方面都有良好的效果。最后,将该模型应用到E. coil细菌基因调控关系的实际数据当中,结果表明,本文提出的正则化模型对基因之间实际存在的调控关系有较好的估计效果,说明该方法在应用中具有良好的适应性。