1. 引言
在统计学教材 [1] [2] 以及时间序列分析教材 [3] 中提到,当研究现象的趋势随着时间的推移呈现出稳定的增长或下降的线性变化,则可用线性趋势方程来对现象进行刻画和分析。当研究现象的趋势随着时间的推移呈现出某种非线性变化趋势,则需要拟合适当的趋势曲线。特别地,如果现象的趋势变化中只有一个拐点,则可以拟合抛物线曲线;如果现象的趋势变化中有两个拐点,则可以拟合三阶趋势曲线;如果现象的趋势变化中有多个拐点,则需要拟合多项式趋势曲线。
刘田和谈进 [4] 从理论上利用局部多项式回归来去除任意序列的确定性趋势,然后利用残差差分序列的方差比进行单位根检验,通过计算结果说明了方法的有效性。沈松英等人 [5] 根据广东省1995年至2009年梅毒发病率的变化特点,选用了多项式趋势曲线和指数曲线对发病率进行拟合,并得到了未来3年的发病率数值。根据计算的结果,作者给政府部门和相关防治机构提供了可量化的参考结果。段树乔和段方婕 [6] 提出了带有电源供给能力约束条件的回归函数筛选及其综合方法,并建立了电网公司售电量的多项式回归预测模型及其检验方法,并通过一个具体实例详细说明了该方法的应用。高峰和余志豪 [7] 利用二次多项式趋势曲线,即抛物线曲线,对浙西地区的农业生产用电市场进行了研究,并基于研究结果提出了今后浙西地区农业生产用电的一些建议。左凯等人 [8] 提出了一种新的确定k阶趋势曲线参数的新方法,并通过我国国内生产总值和金属切削机床产量两个具体的实例分析了新方法的有效性和可行性。
受上述文献以及文献 [9] [10] 的启发,本文将多项式趋势曲线模型引入到白条猪价格指数中,以误差最下为准则确定最优的多项式趋势曲线模型。本文相比于以往的研究文献,主要工作体现在如下两个方面:1) 在确定多项式系数方面,我们采用了局部求和的思想方法而不是传统的最小二乘法方法。这种方法的求解思路简单、计算量小且很容易Matlab编程实现。2) 在模型求解的基础上,进一步讨论了残差的性质。利用时间序列分析理论和统计软件EViews 8.0检验残差是否为白噪声。如果残差为白噪声且模型的精度在要求的范围内,则建模结束。如果残差不是白噪声序列,则需要进一步对白噪声中的有用信息进行提取以建立恰当的时间序列模型。这样可以保证模型在满足精度的要求下,信息量是充分提出利用了的。
本文的结构具体安排如下:第2节给出局部求和方法在多项式趋势曲线模型参数求解中的具体应用,以及残差序列的白噪声检验。第3节以白条猪价格指数为例,以说明多项式趋势曲线在食品领域中的具体应用。第4节给出了本文的结论。
2. 多项式趋势曲线
本小节将具体讨论多项式趋势曲线模型参数的局部求和方法,并给出相应的形式表达式。进一步,利用时间序列分析方法对残差序列进行白噪声检验,以确定所建立的模型是充分提出了数据的信息。
2.1. 模型参数的确定
由文献 [1] 可知,多项式趋势曲线模型的一般形式可表示为
(1)
其中
。关于参数
的估计方法目前有最小平方法,三点法和折扣最小平方法等待,有兴趣的读者可参看相关资料。在这里,我们将采用局部求和的思想方法给出模型参数
的矩阵表达式。
设原始数据是长度为h的非负序列
,其中用于建模的数据为
,用于检验的数据为
。首先,将用于建模的时间序列分成相等的
个数组,每个组的数据有
项。根据趋势值
的
个局部总和来确定参数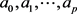 。具体为:设原始观察值
个局部总和分别为
,则有如下关系式
。具体为:设原始观察值
个局部总和分别为
,则有如下关系式
. (2)
在(2)式中分别令i的取值为 1,2,……, p +1 ,于是得到如下方程组
(3)
在方程组(3)中,
的表达式很难给出显示表达式。这里,我们将表达式(3)写成矩阵的形式
为
.(4)
通过求解矩阵方程组(4),即可得到参数
的值,然后代入多项式趋势曲线模型中即得到相应的函数表达式,进而可以计算
的值。
2.2. 计算精度的评估
在选择某种特定的多项式趋势曲线进行计算时,需要评价该模型的计算效果或准确性。评价的方法就是找出计算值与实际值的差距。最优的模型就是计算的误差达到最小的模型,下面给出常见的衡量模型精度的指标。
· 百分比误差(APE)
. (5)
· 平均绝对百分比误差(MAPE)
, (6)
这里
表示的是建模误差,
表示的是拟合误差,
表示的是总的误差。
· 均方根误差(RMSPE)
. (7)
2.3. 残差的白噪声检验及建模
由文献 [3] 可知,白噪声序列是平稳序列,且没有进一步提取信息的必要。因为白噪声序列前后观测值不存在相关关系,即使有历史观察数据对预测也毫无意义。本小节的目的就是继续检验残差序列是否为白噪声,以确定是否有必要进一步研究的必要。
白噪声检验也称纯随机性检验,即检验序列的自相关系数
是否满足
。但是这只是理论上才会出现的理想状况。在实际应用中,由于观察序列的长度总是有限的,导致序列的自相关系数不可能完全为零。为此,我们通过下面的一些准则来判断序列是否为白噪声序列。
时序图判断法:对2.1节的残差序列
作出相应的时序图,如果时序图的值始终在一个常数值上下随机波动,但是波动强度随时间变化不大且没有明显的趋势性和周期性,则可定性的判断出残差序列为平稳序列,或白噪声序列。
自相关系数判断法:如果残差的自相关系数随延迟期数的增加突然或者迅速衰减为在零的周围小幅波动,也可定性的判断出残差序列为平稳序列,或白噪声序列。
P值法:对于残差序列APE,其样本自相关系数记为
,r为指定的延迟期数。构造LB统计量
, (8)
以及原假设
和备折假设
;
. (9)
在原假设
下,给定检验水平为
(本文取
),计算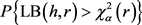 的值,如果
则接受
,认为APE序列为白噪声序列,则建模结束;如果
则拒绝
,认为APE序列为非白噪声序列,需要进一步对残差序列进行建模分析,并将计算的结果反馈到多项式趋势曲线模型的计算值上,从而得到最终的计算值。
的值,如果
则接受
,认为APE序列为白噪声序列,则建模结束;如果
则拒绝
,认为APE序列为非白噪声序列,需要进一步对残差序列进行建模分析,并将计算的结果反馈到多项式趋势曲线模型的计算值上,从而得到最终的计算值。
3. 多项式趋势曲线在白条猪价格指数中的应用
在本节中,我们将以白条猪价格指数为例来说明多项式趋势曲线的应用,其数据来源于全国农产品商务信息公共服务平台(http://nc.mofcom.gov.cn/zhuanti/ap88/jgzs.shtml)的最新数据(星期六和星期日的数据系统没有统计),具体见下面的表1:

Table 1. White pig price index data (2019)
表1. 白条猪价格指数数据(2019年)
对表1的数据,我们分别考虑
,
,
三种类型的多项式曲线进行建模,通过Matlab 2013b编程计算得到他们的数学表达式分别为
· p = 2时的表达式
. (10)
· p = 3时的表达式
. (11)
· p = 4时的表达式
. (12)
通过计算得到相应的数值结果见表2。
从表2可以看出,四阶多项式趋势曲线在建模误差方面是最好的,无论是MAPE还是RMSPE都是最好的,但是拟合误差的值很大,均大于10%。另一方面,二阶多项式趋势曲线和三阶多项式趋势曲线从整体上来看都是很好的,无论是建模误差还是拟合误差都在1.5%一下,并且两个模型基本上精度都是一样的。不过从苛刻的角度来看,三阶还是比二阶有一点点的优势。因此,对于白条猪价格指数我们选择三阶趋势曲线来建模、拟合和预测。
但是,由上面的理论分析我们会问三阶趋势曲线是否完全将历史数据的信息提取出来了呢?针对这一问题,我们将继续对其残差序列进行分析,下面的分析工作是基于统计数学软件EViews 8.0计算出来的,具体见图1和图2。
下面的图1给出了残差APE的时序图,从中可以定性的看出,序列值基本上是在0值附近随机波动,但是波动强度随时间变化并不大,一直在[−2,3]之间波动。进一步,序列值也没有明显的趋势性和周期性。因此,由时序图判断法可以判断残差序列APE为平稳时间序列,或白噪声序列。

Table 2. Computation results of three polynomial trend curves (2019)
表2. 三种多项式趋势曲线的计算结果(2019年)
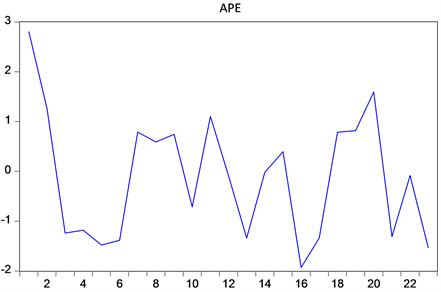
Figure 1. Sequence diagram of residual APE
图1. 残差APE的时序图
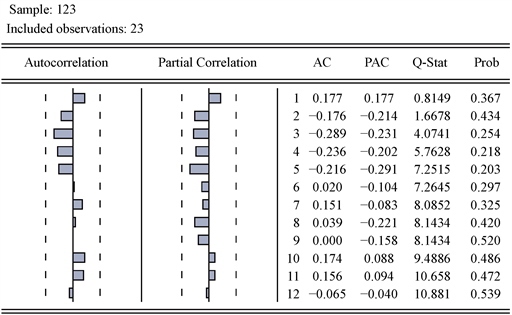
Figure 2. APE correlation coefficient diagram
图2. APE的相关系数图
图2左边显示残差的自相关系数和偏自相关系数都在2倍标准差范围内,且变化范围不大,即两种的值都是非常小的。因此,结合自相关系数判断法可以知道序列值为平稳序列或在白噪声序列。
图2的右边给出的是相应的P值,从计算的结果可知,所有的P值都是大于0.05的。因此,结合P值判断法可明确知道APE序列是一个白噪声序列。即三阶趋势曲线已经将白条猪价格指数的信息提取完全,没有进一步对其残差进行分析建模的必要。基于此,本文的白条猪价格指数的函数表达式为
. (13)
有了方程(13),我们可以预测接下来的几天时间里白条猪价格指数的走势,从而为政府和相关部门制定决策提供可量化的依据,其预测计算结果见表3。

Table 3. Prediction results of trend curves of third-order polynomials
表3. 三阶多项式趋势曲线的预测结果
4. 结束语
本文首先讨论了多项式趋势曲线的参数求解和残差序列的白噪声检验,并通过白条猪价格指数具体展示了如何实现相应的步骤。在传统的预测模型研究中,往往都是以误差最小选择最优的模型,然后对实际问题进行预测,而没有继续讨论模型残差序列的性质。本文与之前的工作相比较,利用时间序列分析方法讨论了模型残差是否为白噪声。只有在残差序列为白噪声的基础上,才可以进一步对所讨论的进行预测分析。在今后的研究中,可将此思想应用在其他类似的统计预测模型中。
基金项目
成都师范学院大学生创新创业训练计划项目(201814389100)。
NOTES
*通讯作者。