1. 引言
从描述自然现象的方程结构角度来看,自然界的规律可粗分为两大类:局域规律和整体规律。前者用微分方程描述,后者用积分方程描述。由于深信局域性和因果性为基本物理现象的内秉特性,即时空每一点上的物理量变化率只受其临近点上其它物理量所贡献,不会即时受到来自遥远时空点上的物理量的影响,因此过去物理学基本方程都是微分方程,而非积分方程。当然,积分方程也是存在的,它们多因考虑了非基本的复杂关联过程所致,例如,众所周知,统计物理学所介绍的描述普通流体系统中原子、分子碰撞及宇宙热力学系统中基本粒子散射的玻尔兹曼积分微分方程,其在相空间(动量–坐标六维空间)内的分布函数的演化率受非平衡碰撞项的相空间积分贡献所影响。有的方程即使不具有积分形式,但其实也考虑了整体平均效果。一个最简单的例子是导体内欧姆定律的微分方程
(其中
为电流密度,
为电场强度)。按照基本物理定律,此方程有太多“自我矛盾”之处,如按照牛顿第二定律,电荷的加速度应该与电场强度
成正比,但在这里,方程左边电流密度是
,因此在欧姆定律中电荷速度
才与电场强度
成正比,“不符合”牛顿运动定律;按照Galileo变换,电荷速度
可以变换为零,而电场强度在Galileo变换下不变(在相对论Lorentz变换下,电场强度
才变化,但如果参考系速度很小,也可以看作其不变)。欧姆定律违反Galileo相对性原理,这也是一个“矛盾”。但是实际上,从推导欧姆定律的微分方程的过程看,该定律描述的并非是基本的物理过程,而是包含了电荷受电场加速和受正离子热散射两种作用下的复杂驰豫过程,含有了整体平均过程(例如上面的电荷速度
,也并非电荷瞬时速度,而是平均效果)。除了以上非基本的或复杂的物理过程包含整体性外,物理学如量子力学还提出了其它更多的整体效应或现象,如波函数塌缩与规范势(联络)的积分效应。前者的典型例子是量子纠缠波函数(或状态矢量)的非局域、超空间、超光速的隔空关联塌缩这一类似“超自然”的现象(这方面涉及量子力学基本解释。各种诠释和流派争论很多,其也非本文关注的对象,不必赘述),后者是与几何相位有关的拓扑、整体效应,在大量物理系统中都有所体现 [1] [2]。本文主要叙述与几何相位、规范势有关的整体物理现象以及它们与一些微分几何概念的关系。
我们对整体现象其实并不陌生。在欧几里德几何中,任意三角形内角和都等于180度以及任意n边形内角和为
度,就是典型的整体现象。尽管在历史上整体效应时有提出,但物理学中第一个著名的整体效应是提出于1958~1959年的Aharonov-Bohm效应 [1] [2]。在经典电动力学中,有物理意义的场量是电场与磁场,四维电磁势被当作是辅助量,并非有物理意义 [1] [2]。但是在量子力学提出后,这种观念受到了挑战,因为至少在荷电粒子的Schrödinger方程中,直接出现的是四维电磁势,而非电场与磁场。Aharonov与Bohm提出了一个有趣的效应,让电子发生类似光学中的双缝干涉现象,即两束从同一源出发的电子束沿着两条不同的路径传播然后汇聚在屏上。此两条路径构成一个闭合环路,设该环路内被一个磁通量穿过 [1] [2],这样在屏上会出现与磁通量有关的干涉现象,如磁通量发生改变,屏上的干涉条纹也跟着改变。需要注意的是:磁通量被聚集在一个小“管子”内,不发生磁漏,因此电子束在路径上并没有受到任何磁力的作用。按照经典电动力学的观点,这种受磁通量影响的干涉是不可能发生的(如果发生,在经典电动力学看来,似乎发生了“超距”作用) [1] [2]。但在量子力学中,这种“超距”作用却要求发生。这是因为,虽然在没有磁场的区域,磁感应强度
为零,但是其磁矢量势
却不为零(与经典电动力学认识不同,在量子力学中,
是有物理意义的),电子和场的相互作用Lagrange密度是
(电流密度
与磁矢量势
发生了耦合) [1] [2]。从这个角度讲,这种所谓的“超距”作用其实并不违反狭义相对论,但是Aharonov-Bohm效应体现了量子力学波函数在磁场中的整体拓扑效应,因为被电子路径包围起来的磁通量影响了电子波的干涉 [2]。如果磁通没有被电子束路径包围(磁通位于电子束路径外面),那么这个磁通就不会影响电子物质波的Aharonov-Bohm干涉。
除了Aharonov-Bohm效应 [1] [2],量子力学还有一个拓扑效应是磁荷(磁单极子) [3] [4] [5] [6]。我们知道,在Maxwell方程中,电与磁的地位并非完全等同,如自然界有电荷,但无磁荷。当然,这个现象可以用磁矢量势
的性质解释:
(旋度的散度必为零)。英国理论物理学家Dirac在1931年指出,假如磁单极子(磁荷)存在,我们不但可以将Maxwell方程组写得更为电磁对称,而且由此(利用波函数单值性以及规范不变性)可解释电荷的量子化起源 [3]。磁荷作为磁场的源,方程
变为
(
为磁荷密度)。显然,在这里,磁荷不同于电荷,磁荷是一种拓扑荷 [3],它使得三维磁矢势
变为非解析函数,即它的两个偏导数不可交换(所谓非解析函数,它是这样一种函数,它导致
),从而我们有
。我们知道,
是电磁学Bianchi恒等式之一,它只在当三维磁矢势
是解析函数时才成立。在Maxwell理论中,另一个Bianchi恒等式是Faraday电磁感应定律。当有磁荷存在时,三维磁矢势
就不再是解析函数了(它在磁单极子所在位置有畸点。在畸点处,偏导数不可交换)。磁荷(假设它存在)让Maxwell方程中的Bianchi恒等式不再成立,所以磁荷是拓扑荷。
其实,Aharonov-Bohm效应 [1] [2] 和磁荷(磁单极子) [3] [4] [5] [6] 这两个拓扑整体现象 [2] 并不限于只出现在我们所熟悉的电动力学内。一切局域规范理论(包括Yang-Mills非阿贝尔规范理论、广义相对论引力理论以及各种引力规范理论)中都可能存在该类整体效应。譬如,我们知道爱因斯坦广义相对论引力场方程在弱场低速近似下可以具有Maxwell方程组的形式,故而一切Maxwell电动力学现象,都可以在广义相对论引力理论中寻找到其对应的物理现象。这里可以介绍一下所谓的引力磁荷(gravitomagnetic charge),它是电磁学中磁荷的类比物。引力磁荷也可以称为引力磁质量(gravitomagnetic mass)、对偶质量
(dual mass)。我们把通常的具有质量的物质称为引力电性物质,质量就是引力电荷量,其引力场分布由爱因斯坦引力场方程决定。与此相对应,我们可以提出引力磁性物质和引力磁荷(对偶质量)的概念,并建立引力磁荷的引力场方程。从对引力场方程的弱场低速近似形式和对偶方程
静态的球对称精确解的分析可以看出,引力磁荷的存在与引力场的度规
的畸点(非解析性)有关。引力磁荷(对偶质量)与引力电荷(质量)不同,它是时空的拓扑荷,因此引力磁荷的引力场方程和运动方程的弱场近似形式类似于电动力学中磁单极子的电磁场方程和磁单极子运动方程。与电动力学中的磁荷一样,引力磁荷在宇宙中倒底是否确实存在,其实难以回答。也许引力磁荷可能以点粒子形式存在,也有可能以一定体积(有限大小)的所谓拓扑性孤粒子(topological soliton) [7] [8] 形式存在(类似在非阿贝尔规范理论中’t Hooft-Polyakov拓扑磁荷孤粒子 [7] [8] )。
上面所介绍的Aharonov-Bohm效应 [1] [2] 和磁荷(磁单极子) [3] [4] [5] [6] 这两个拓扑整体现象都可以通过带电粒子波函数的相位体现出来。实际上,磁通量就是这样一个相位。显然这种相位不同于普通的动力学相位。平常所熟悉的动力学相位取决于粒子或系统的能量、动量等。到1984年, 由于Berry的工作 [9],物理学家明白量子力学的相位包括两种,即普通的动力学相位(dynamical phase)和体现整体、拓扑效应的几何相位(geometric phase) [9] [10]。文献 [2] 认为,尽管“拓扑”与“几何”在数学上差别很大,但是在物理学几何相问题中,拓扑、几何、整体此三术语意思相近,它们总被联系在一起。
下面从本人的理解角度来阐述这两种相位的关系和来源(它们可能只反映个人的一家之言):我们知道,
在量子力学中,如果哈密顿量
是定态(即不含时间)的话,那么Schrödinger方程
可以化
为定态方程
,此方程可以求解,且相位因子是
。但是如果哈密顿量
含有时间参数,即
,那么
还成立吗?如果成立,则能量本征值E变为一个瞬时能量本
征值
,那么相位因子
还成立吗?一般人可能认为这两条猜测都成立;或认为即使不
成立,至少在绝热条件下(即哈密顿量
随时间变化极度缓慢时)此二猜测可能成立。即使在绝热条件下,
上述猜测不成立,根据计算,波函数可以出现一个新的相位因子
,其中相位为
[11]。在Berry之前,很多人对这个相位不以为然,认为它不重要,可以略去 [11]。但Berry发现,这是一个非平庸的相位,它在循环(巡回)条件下,可以写为Aharonov-Bohm相位那种闭合环路积分形式 [9]。
例如我们假设有一个参数空间中的物理量
,那么
可以写为
,这个形式非常类似于Aharonov-Bohm相位中磁矢量势
与路径线元
的点乘的积分,
就好比磁矢量势
[9] [10] [11]。由于
并非是一个全导数(不是一个标准的梯度),因此它的旋度(等效
的磁场)必然不为零(只有梯度的旋度才为零)。因此这个相位具有物理含义,不可被忽略 [11]。经过对
的闭合路径积分之后,相位
被称呼为Berry相位(Berry相位是一种绝热循环几何相位 [9] [10]
[11]。所谓循环条件,是指哈密顿量算符经过一段时间演化后,最终可以复归为初始哈密顿量)。而
中的
只是一个普通的动力学相位。
我们可以将这种等效的“磁矢量势”
写为
形式(这里的梯度算符
既可以代表
三维普通空间中的梯度,也可以代表哈密顿量算符抽象的参数空间内的梯度)。可以证明,在规范变换下,
满足规范势的变换规则。如假设对波函数
施行一个阿贝尔U(1)规范变换
,那么
。设
(归一化),那么此变换规则与磁矢量势
的规范变换
具有一样的结构(对于非阿贝尔规范变换,也可以作类似讨论。这里略)。由于规范变换
中的参量
是一个解析函数,根据Stokes定理,
的闭合路径积分为零(即
),所以Berry相位
具有规范不变性(只要有规范不变性,自然就有物理含义了,也即实验上
可测了。在这里,规范不变、物理含义、实验可测,此三词具有同一意思)。在1983年Berry的论文因为被审稿人弄丢而耽误发表之前 [2],数学家Simon在听了Berry的口头阐述后,发现Berry相位与纤维丛微分几何中的Chern氏类(Chern class)有关,并把这一相位命名为Berry相位 [2]。因此Simon的论文(1983)发表在Berry的论文(1984)之前 [12]。由于几何相位与规范场有关,而规范场又与微分几何纤维丛有关,那么将含时(或含演化参数物理体系的)几何相位与微分几何纤维丛概念联系起来 [12],也是顺利成章的了。
在Berry 1984年发表的理论工作之前,实验物理学家其实已经在多个实验 [13] [14] [15] 中注意到了几何相位的存在 [2]。如1938年苏联Rytov [13] 和1941年苏联Vladimirskii [14] 提出了非均匀介质中的Rytov-Vladimirskii光波极化面偏转效应。由于光波在非均匀介质中传播,且电磁场
、
与传播方向(即波矢量
)要强制构成右手螺旋定则,那么在光波平行移动一周后,光波偏振极化矢量不再与初始状态一致 [2]。1956年印度人Pancharatnam也研究过能改变光波极化偏振面的光学材料中的光波偏振的改变问题 [15]。在以上这类问题之中,局域地看,似乎光波在介质内每一点都没有发生偏振面的改变 [2] (这就像广义相对论弯曲时空中每一点都镶嵌了局域Minkowski惯性系一样),但是光波在路径上循环一周,却出现一个不可积的整体相位 [2]。在1986年,这类光波偏振改变现象由Chiao和Tomita等人再次领悟到,他们使用非共面(noncoplanarly)螺旋弯曲(coiled)光纤实验进行研究 [16] [17]。光子在螺旋弯曲光纤内传播,最终会多出一个与螺旋光纤几何弯曲有关的几何相位(这个几何相位在数值上正比于光子波矢量
在扫描过程中所张开的立体角)。我们知道,立体角大小正比于立体角所对的球冠的面积,因此几何相位正比于通过球冠的某种“磁场”通量 [16] [17] [18]。这个通量来自于等效的“规范势”(物理学语言)或联络(微分几何语言)的曲率与球冠面积的乘积。螺旋弯曲光纤中的光波几何相位既可以用经典电磁波理论、微分几何理论、Berry量子力学方法研究 [16] [17] [18] [19] [20],也可以用电磁场量子化方法研究 [21],在后者的框架下,Gao发现极化光子态会出现量子真空水平上的几何相位,但因为介质的各向同性,左右圆偏振的真空模式几何相位恰好抵消而难以显现 [21]。
在上面的Rytov-Vladimirskii [13] [14]、Pancharatnam [15] 以及Chiao-Tomita [16] [17] 三个效应中,有一个共同特点,就是光的波矢量
是演化着的(要么在非均匀介质内演化,要么在螺旋弯曲光纤内演化),
的方向是时间的函数,因此波函数(光波或光子偏振状态矢量)在动量空间(
参数空间)中演化 [16] - [21]。这也可以默认为光波或光子与非均匀介质或螺旋弯曲光纤之间的耦合哈密顿量是一个在时间上的演化算符。由此,物理学家们认识到,只要哈密顿量算符有一个演化的参量(这种参量既可以是时间,也可以是其它任意发展参数 [21] [22] [23],包括上例在螺旋弯曲光纤内的光波波矢量
[21] ),那么量子态矢量就有可能出现几何相位。参照这条标准,那么能呈现几何相位的物理系统就实在是太多了。例如量子力学教科书中经常提到的氢分子振动,两个氢原子之间的距离R是时间的函数,因此对于每个氢原子内的电子而言,它的哈密顿量就不再是定态的了,而是有一个演化参数
[22] [23]。那么这样的分子系统,就会出几何相位。因此,几何相位在分子化学反应中也有贡献,能影响分子化学反应速率和反应通道 [22] [23]。
对物理系统而言,动力学性质其实总比拓扑性质重要得多,但是因为前者所研已经近乎完毕,后者才被重视起来。在规范理论中,拓扑性质系因规范势有畸点、不再是解析函数所致。但本文并不专门研究这些规范势所带的畸点,而是研究演化系统所需要的描述量,如标架场、联络以及它们与规范理论的关系。此文中的概念和方法可能可用于理解和研究某些课题中的问题,包括经典电磁光学、量子光学、约束体系量子力学、规范场论、广义相对论、引力–规范统一场论以及其它非基础物理学科的专题如机械力学、金融物理学等领域内的部分现象。本文只反映个人的一点浅见,希冀起到抛砖引玉的效果。
2. 演化系统理论研究方法
我们介绍一下研究量子演化系统的一般理论方法。在上面介绍的绝热几何相位
中
[9] [10] [11],状态函数
是瞬时定态Schrödinger方程
的瞬时本征态。但在这里要指出,“瞬时定态Schrödinger方程”和“瞬时本征态”这两个概念在本质上是错误的。它们是不应该存在的概念。实际上,一旦哈密顿量算符含时,瞬时定态Schrödinger方程
便不再严格成立,只有
原始的Schrödinger方程
才仍旧成立。那么几何相位
中的状态函数
是什么?如果它是Schrödinger方程
的解,但是Schrödinger方程的解又含有几何
相位因子
,几何相位
也含有Schrödinger方程的解(态函数
),这一逻辑很不自洽。所以,料想几何相位
中的状态函数
不可能是Schrödinger方程的解。研究者相信,存在某个算符
,它具有本征值方程
,其本征态就是几何相位
中的状态函数
。1969年Lewis和Riesenfeld提出了一个不变量理论 [24],解决了这个问题。在该理论中,不直接求含时Schrödinger方程
,改求某个不变量
的本征值方程
,而Schrödinger方程的解
与
不变量
的本征态
只相差一个相位因子,该相位因子的相位为(非循回)几何相位与动力学相位之和
[24]。Lewis-Riesenfeld不变量
满足(或定义为):
[24]。此方程右边为零,体现
不变量
的本征值
是一个常数(守恒量)。读者也许可以看出,此方程是分析力学中正则哈密顿方程的量子力学版本(对守恒量)。这样,根据Lewis-Riesenfeld不变量理论 [24],含时Schrödinger方程
的特解为
,相位
,其中
是普通的动力学相位,
是非循环、非绝热过程中呈现几何特性的相位 [24]。含时Schrödinger方程
的通解为上述所有特解的线性叠加。虽然Lewis-Riesenfeld理论早在1969年提出 [24],但是当时并没有对后一相位的几何整体特性作特别钻研。
我们可以看出,Lewis-Riesenfeld理论并没有直接求含时Schrödinger方程的解,而是改弦易辙,把目
标放在求不变量本征态上。这也说明,Lewis-Riesenfeld不变量
方程
和
[24] 合在一起时具有含时Schrödinger方程
的功能。态的演化,其实
就是满足某个么正群对称性下的么正变换。此二法(即不变量方法 [24] 与Schrödinger方程法)都是同一么正群的不同的等价表示而已。这让我们回忆起规范理论中的另一个现象:矢量规范场与物质场都是么正群的表示。确实如此,无源矢量规范场方程即Yang-Mills方程
[25] 与Lewis-Riesenfeld不变量
方程
[24] 在结构上比较相似(只不过前者定义在四维时空内,
后者仅仅定义在一维时间上);物质场方程如狄拉克方程和Schrödinger方程都含协变导数
,
而含时方程
也含有协变导数,即
,故而两者在结构上也十分相似。
这样一比较,我们认识到Lewis-Riesenfeld不变量 [24] 为什么必须呈现的理由了。具体说来, 类似群有基础表示,同时也有伴随表示一样,Lewis-Riesenfeld不变量方程(正则哈密顿方程的量子力学版本)好比是Schrödinger方程(基础表示)的伴随表示(这是作者个人的一家之言)。
当然,Lewis-Riesenfeld含时不变量
[24] 的本征态仍旧难以求解。于是在1991年,Gao等人提出了一种么正变换方法(全名叫“与不变量有关的么正变换方法”) [26]。通过对不变量
的本征值方程
、不变量方程
[24] 以及含时Schrödinger方程
三者
施行么正变换
[26],将含时不变量
化为了一个不含时的不变量
,该么正变换总的思想是将含时不变量
和含时哈密顿量
对角化,这样求解就变得更为容易 [26]。经过么正变换,新的哈密顿量
算符变为
[26]。如此一来,新的一项
的规范势特点十分明显。这样的结构,显然满足普通的规范变换。新的这一项
(可以称为几何相联络或几何相规范势)
会导致几何相位。几何相位与该系统哈密顿量参数空间中的几何构型有关 [26] [27] [28]。如果哈密顿量不含时,那么这样的么正变换也是不含时的(即在时间轴上,这是一个整体规范变换,不再是一个局域规范
变换了),新的这一项
就变为零了,量子系统也就不含几何相位了。
不变量理论 [24] 及其么正变换方法 [26] (应用广泛 [27] [28] ),其意义有:(1) 将量子力学算符方程化为了不变量算符内的参量代数方程(虽然这组方程是非线性的,仍旧难以求解,需要依靠数值计算),使得求解在形式上变得容易;(2) 回避了量子力学复杂的编时乘积和时序算符方法。我们知道,在Schrödinger
方程
中,如果哈密顿量
不含时,那么方程的形式解很简单,它是
。但是如果哈密顿量
含时,有人如果要将Schrödinger方程的解写为
,这就错误。这是因为不同时刻的哈密顿量如
与
不可对易,
上面的解并不正确。不可对易算符的微积分与传统可对易数的微积分大不相同,前者十分复杂,涉及编时乘积问题。而Lewis-Riesenfeld不变量方法则回避了这个难题,因此该方法可望在量子场论中也有应用意义 [27] [28]。
对于量子力学系统,根据不同的参数条件,有三种相位值得注意,分别是:Berry相位(它是绝热、循回几何相位) [9]、Aharonov-Anadan相位(非绝热、循回几何相位) [29]、Lewis-Riesenfeld相位(非绝热、非循回几何相位) [24]。后者便是在Lewis-Riesenfeld不变量理论中计算得到的相位。Berry相位和Aharonov-Anadan相位因为是在哈密顿量参数在循回条件下定义,其拓扑秉性最为明显,即其相位大小就是哈密顿量参数空间内量子系统演化路径所张开的立体角 [9] [20]。Lewis-Riesenfeld相位的这一拓扑特点不明显 [24],但是值得一提的是,它的微分形式也具有立体角微元的形式,因此在局域意义上,我们认为其亦有拓扑秉性。
我们叙述了有关几何相位的研究历史。下面扼要说明一下其应用。上面已经提到,只要哈密顿量含有演化参数,量子系统必然呈现等效的规范势、等效的“磁场”和通量,出现几何相位。这样的系统比较容易在实验上构造。几何相位因为其无色散性 [2]、规范不变性,不受动量和能量等动力学物理量的直接影响,只与参数空间演化路径几何构型有关,因此,几何相位在物理学各个分支中都有研究,包括量子力学 [30] - [36]、量子光学 [37] [38] [39] [40] [41]、原子物理学 [42] [43]、核物理学 [44]、规范理论 [45]、引力理论 [46]、凝聚态物理学 [47] [48]、分子物理/化学反应等领域 [49] 和量子计算 [44] [50] 等。具体介绍各个应用并非本文重点,但我们可以举若干简单例子(这些例子中的哈密顿量数学形式在后半文需要涉及)。
3. 几个含时演化量子系统
在这里,我们举若干含时演化量子系统的例子。这些例子包括:约瑟夫森隧穿电流效应、二能级原子在经典光场下的Rabi振荡、运动中子或电子磁矩与电磁场的耦合等。
如果两块超导体之间有(使用某种介质或真空间隙隔离的)弱接触或弱连接(根据简要分析或者根据有关固体理论、超导物理学或量子物理学专著 [51],研究人员知道可以用几纳米到几十纳米厚的绝缘体材料形成弱接触或弱连接;对于自由电子密度越大的弱连接材料,间隙厚度允许更大一点,例如一些资料如 [51] 所引用的超导隧穿电流文献表明,由于超导电子库伯对本身几何尺寸或空间上的相干长度有微米或若干微米量级 [11],那么使用稍厚一点的几百纳米宽的半导体材料或更厚的几千纳米尺寸的金属材料来连接该两超导体,也有可能造成两块超导体之间的弱连接效果 [51] ),超导体之间就有隧道贯穿电流,此谓约瑟夫森(Josephson)隧穿电流效应,两块超导体之间的电子库伯对波函数相位之间有关联 [51]。这是比较容易理解的,因为电子库伯对的波长比较长,长于弱接触间隔距离。我们设左右两块超导体内的库伯电子对的波函数分别是
和
,那么约瑟夫森隧穿效应的费曼方程是 [51]。
。
该方程也可以写为矩阵形式
。
上述Schrödinger方程的哈密顿量H可以写为三个泡利矩阵的线性叠加。这类方程比较典型,除了约瑟夫森超导结,很多二态系统(如二能级原子、在磁场中进动的电子或中子自旋、耦合波导体系如两根临近波导线之间的耦合系统)以及所有哈密顿量满足SU(2)群结构的体系的动力学效应均可以用该方程来描述(以上这些体系可在量子力学、量子光学以及导波光学教材内找到)。如果哈密顿量不含时间,那么该系统没有几何相位。如果耦合系数K有一含时因子,如
(这可以通过添加一个磁通量来实现,磁通量可以让约瑟夫森效应耦合系数K由实数变为复数) [51],那么此时描述约瑟夫森效应的费曼方程是
,
。
我们可以定义一个新的波函数
,
。于是计算得到
;
。
我们希望
、
,也就是
。那么
和
就化为了如下形式
,
。
为了方便,我们可以将哈密顿量写为三个泡利矩阵的线性叠加,由此要求
,也
即
。于是,我们可以取
(其它虽满足
但不满足
的
也是允许的。所有多种选择之间无非仅仅差了一个或几个幺正变换)。现在我们看到,原本耦合系数含有“时谐振荡因子”
的哈密顿量,通过一个幺正变换,就变为了不含时的哈密顿量。由此说明,耦合系数含“时谐振荡因子”的哈密顿量系统,不带有几何相位。但是,如果哈密顿量的耦合系数含时因子不能写成时谐振荡因子
,那么就不存在这么一个简单的幺正变换,因此也就无法将含时的哈密顿量变换为定态(不含时)的哈密顿量,这样的系统肯定会携带几何相位。
上述超导约瑟夫森效应方程的矩阵形式的哈密顿量可以写为三个SU(2)生成元的叠加形式:
。
以上已经将哈密顿量参数化了。我们由此可以得到如下一组关系:
,
,
及
。
二能级原子系统(在光场驱动下)的几率幅方程 [52] [53] 与约瑟夫森效应的费曼方程 [51] 在数学结构上是一模一样的。这可以讨论如下:设二能级系统
的几率幅为
、
(
是低能级、
是高能级),频率失谐
定义为
(
是跃迁频率,
为驱动
跃迁的光场的频率),按照量子力学Schrödinger方程,二能级原子系统(在光场驱动下)的常用的几率幅方程是 [52] [53]
,
。
此方程在所有量子光学教材中都能找到。为了能将它的哈密顿量写成三个泡利矩阵的组合,我们重新定义几率幅:设
,
,于是计算如下
,
。
我们就有新的几率幅方程
,
。
它可以写为矩阵方程形式
。
此方程在数学结构上与约瑟夫森效应的费曼方程是一模一样的(
,
,
)。
当然,我们也可以有更为简单的论证:在如下方程
的基础之上,在哈密顿量上可以新添加一个单位矩阵的能量算符,即
。
于是只要定义
,我们就有
。
从而有
。
最终我们得到矩阵形式的新的几率幅方程:
。
在中子、电子自旋磁矩与磁感应强度相互作用的体系中,哈密顿量是
。如果在空间上放置一个电场
,那么在运动的中子或电子看来,根据相对论电动力学,电场会感应出一个磁感应强度:
。于是自旋磁矩与磁感应强度的耦合哈密顿量是
。 令
,那么自旋粒子与场的耦合哈密顿量是
(其在数学结构上类似于电流与磁
矢量势的耦合)。由于
中的磁矩
含有自旋算符(SU(2)规范群生成元),那么
就是一种非阿贝尔(磁矢量)规范势。类似的,对二能级原子也可以作类似操作。如在前述与光波发生电偶极相互作用的原子体系中,其Rabi频率 为电场与电偶极矩的点乘,如果在空间中放一个磁场,那么在运动原子看来,这个磁场就会感应出一个电场
,于是在效果上造成了电偶极原子与磁场的耦合。那么类似上面的讨论,也可以出现类似
这样的耦合哈密顿量,它在效果上表现为某种流与某种非阿贝尔“磁”矢量势
的耦合。如果
是阿贝尔规范势,那么与哈密顿量有关的相位十分简单,只要计算哈密顿量的时间积分即可,如
。但是在上面的例子中,
是一种非阿贝尔“磁”矢量规范势。直接计算
积分一般是错误的(除非不同位置上的“磁”矢量规范势
的分量可以彼此对易)。在非阿贝尔形式的哈密顿量
中,等效“磁”场(曲率张量或规范场张量)是
。上述的电子、中子或二能级原子会受到与
有关的等效Lorentz“磁”力,因此处于不同自旋态或者不同能级态的原子受到的Lorentz“磁”力并不相同,这是类似自旋Hall效应的一种现象。
为电场与电偶极矩的点乘,如果在空间中放一个磁场,那么在运动原子看来,这个磁场就会感应出一个电场
,于是在效果上造成了电偶极原子与磁场的耦合。那么类似上面的讨论,也可以出现类似
这样的耦合哈密顿量,它在效果上表现为某种流与某种非阿贝尔“磁”矢量势
的耦合。如果
是阿贝尔规范势,那么与哈密顿量有关的相位十分简单,只要计算哈密顿量的时间积分即可,如
。但是在上面的例子中,
是一种非阿贝尔“磁”矢量规范势。直接计算
积分一般是错误的(除非不同位置上的“磁”矢量规范势
的分量可以彼此对易)。在非阿贝尔形式的哈密顿量
中,等效“磁”场(曲率张量或规范场张量)是
。上述的电子、中子或二能级原子会受到与
有关的等效Lorentz“磁”力,因此处于不同自旋态或者不同能级态的原子受到的Lorentz“磁”力并不相同,这是类似自旋Hall效应的一种现象。
与不变量有关的幺正变换理论 [26] [27] [28] 是用来将哈密顿量算符对角化的有效方法。通常使用了该幺正变换方法,还必需使用Baker-Campbell-Hausdorff公式 [54],以便计算经过了幺正变换(与不变量有关)
之后的新的哈密顿量
(尤其是几何相规范势
)。不过对于三生成元量子系统(即
哈密顿量算符可以写为某李代数三个闭合、完备的生成元的线性叠加),其实可以不必使用该幺正变换方法;即使使用了该幺正变换,也可以避开使用Baker-Campbell-Hausdorff公式。对于生成元多余四个的哈密顿系统,使用与不变量有关的幺正变换理论方法 [26] 可能是避免不了的,使用它,应当可以为计算带来大量方便。下面介绍本专题的基本计算方法(Lewis-Riesenfeld不变量理论 [24] 及其幺正变换方法 [26] ),其余进一步论述与讨论,则属于笔者个人的思考和总结。
为了便于叙述含时量子系统的计算过程,有必要对Lewis-Riesenfeld不变量理论 [24] 的要点进行总结。Lewis-Riesenfeld不变量理论的要旨可以用如下几个公式概括 [24]:含时Schrödinger方程是
,它的解可以写为
,其中
是
Lewis-Riesenfeld不变量算符
的本征态:
。此不变量
满足方程
。含时Schrödinger方程解析解
中的相位为
。这个相位为两部分之和。我们可以分别称呼其为动力学相位(与哈密顿量算符
有关)和几何相位(与导数算符
有关)。我们的任务就落实于求解
Lewis-Riesenfeld不变量方程中的不变量算符
以及本征值方程(
)。
不少量子力学系统的哈密顿量具有某个李代数结构,它们往往是李群生成元的线性组合。所包含的李群可以多种多样,如SO(2)群、SU(2)群、SU(1,1)群、SO(3)群、SU(3)群等。例如经典光场与二或三能级原子的相互作用,其哈密顿量为SU(2)或SU(3)李代数生成元的叠加;量子化光场与二或三能级原子相互作用,即用所谓Jaynes-Cummings模型描述 [55],其哈密顿量具有超对称李代数结构(尤其是当二能级跃迁过程中同时牵涉到多个光子的吸收和发射 [56] [57] [58],那么光子-原子相互作用哈密顿量更能体现超对称代数结构 [56] [57] [58] [59] [60] )。哈密顿量内李代数生成元越多,计算越复杂。因此我们在这里选择尽可能少的系统来研究,钻研本主题微分几何概念。SO(2)群过于简单,SU(2)群、SU(1,1)群、SO(3)群是最合适的手工分析对象。在本主题中,我们选择简单的SU(2)群结构的哈密顿量来研究(因为对它我们可以进行手工计算。当然对SU(1,1)群、SO(3)群也可以进行手工计算,只是它们所对应的物理系统不如SU(2)群那么广泛),但其结果对其它群结构的哈密顿量系统也有借鉴意义。
4. 几种计算态矢量与相位的方法
1) 使用不变量理论, 但不使用幺正变换方法:
我们的讨论是以三生成元哈密顿量体系(磁场中的自旋磁矩粒子)为例。设Lewis-Riesenfeld不变量算符
空间矢量可以写为
,那么不变量算符
可以写为
,
其中算符
。在下面的计算中我们针对自旋1/2的自旋角动量算符(
,
为三个泡利矩阵)。众所周知,
的本征值方程
很容易求解(可见一般量子力学书籍中的自旋章节 [55] )。如果
的本征值只有两个(
),那么
的两个本征态矢量是
,
。
这组解满足完备性条件:
(
是二维单位矩阵)。这个量子系统的哈密顿量算符可以写为
,其中
是含时任意矢量参数, 我们可以取作
。
在矩阵表示下,这个哈密顿量算符可以写为
。
下面我们来计算哈密顿量算符的期待值(在不变量本征态
下):
。
不变量本征态
的时间导数是
。
这样,
等于
。
于是含时Schrödinger方程(对应不变量本征态
)的解的相位变化率是
。
我们也可以求解哈密顿量的另一个期待值(在不变量算符另一个本征态
下)以及Schrödinger方程的解的相位,这个相位是上述情形相位的−1倍(过程略)。
2) 使用幺正变换方法 [26],但避用Baker-Campbell-Hausdorff公式:
下面的式子对于我们的计算用处很大,所以我们先列出来:
,
其中单位矢量
满足:
。
我们来考虑一个如下的幺正变换(这是与不变量有关的幺正变换 [26] )
。与上面的式子比较,我们可以得到
,
,
,其中
,
,
。于是我们得到如下两个关系:
,
。
这样
可以写为矩阵形式
。
我们因此可以定义:取
为正数,且将
、
参数化,即
,
,我们就有幺正变换
。
注意不变量算符 [24] 与哈密顿量算符都是同一组闭合(完备)生成元的线性叠加 [26]。上面已经选取
与
是不变量算符的参数,即
。
根据已有经验,在这个问题中,与不变量有关的幺正变换(此问题的幺正变换思想源泉见文献 [26] )应当就是
,
。
这是一个么正变换算符,满足
(单位矩阵)。
下面我们来计算不变量算符I的幺正变换。计算如下:
由此看出,不变量算符I变为了SU(2)群第三个生成元(此为文献 [26] 关于改造不变量算符的思想要旨之一)。么正变换将含时不变量I变为了不含时的不变量
,并且不变量也被对角化了 [26]。
哈密顿量H的幺正变换为:
,其中
其中矩阵元的各个元素为
进一步可以写为
矩阵非对角元
与
需要特别关心。它们可以写为:
,
。
我们进一步计算
(此可以称为“几何相联络”):
于是
为
那么在幺正变换后的哈密顿量
内,矩阵右上角元素为
考虑Lewis-Riesenfeld不变量方程
[24],得到一组复杂的非线性方程
,
。
于是我们可以有
。
那么可以证明新哈密顿量
矩阵右上角元素为零。计算过程如下:
。
同理,在新哈密顿量
内,矩阵左下角元素也为零。最终我们可以得到幺正变换后的新的哈密顿量为
。
由此可见,经过么正变换 [26],含时哈密顿量变为了一个对角化的简单哈密顿量。
3) 既使用幺正变换方法,也使用Baker-Hausdorff公式:
在用与不变量有关的幺正变换计算动力学相位时,需要用到如下的Baker-Hausdorff公式 [61]
对于该公式,很多量子力学教材或者习题集均有证明 [61]。为了方便读者(尤其为了下面需要继续讲
解的计算几何相联络
的多种方法),这里简述如下:
设
,
为某个实参数。下面我们计算算符
的一阶、二阶、三阶关于参数
的导数 [61]:
,
,
我们因此可以利用泰勒级数对
展开,并将上述结果代入泰勒级数,得到
最后令
,那么就可以得到上式 [61]。
值得一提的是,算符B并不仅限于矩阵算符,微分算符其实也是允许的。由于在计算几何相位时,
我们需要计算
,为此我们可以计算如下:
设
,
,我定义
(
是参变量,本身不含时间,时间含在矩阵算符L
内。注意:L与
不对易)。下面我们求出
的一阶、二阶、三阶导数:
,
,
,
当
趋近于零时,
,上面结果变为
,
,
,
我们可以利用泰勒级数对
进行展开,并将上述结果代入泰勒级数,得到:
最终令
,我们就得到 [26]
此公式对于计算几何相位或者几何相位联络十分有必要 [26] [27] [28]。
与不变量有关的幺正变换方法 [26],其用途要旨就在于将不变量算符对角化,最终将哈密顿量对角化,从而获得精确解(解析解)。当然,这个精确解的最终获得,还需要求解一套非线性辅助代数方程(
和
的方程) [在文献 [26] 中,这类方程被称呼为辅助方程]。由Lewis-Riesenfeld不变量方程
[24] 得到的非线性辅助代数方程是
,
。这实际上是将Lewis-Riesenfeld不变量算符方程代数化 [26]。该辅助代数方程是关于求解Lewis-Riesenfeld不变量算符
中的含时参数的方程 [24] [26] [27] [28]。
在计算几何相位时,总是牵涉到计算规范势算符(或几何相联络)
。上面实际上已经有两种方法获得
的展开式:第一法是在
展开式中,将B看作时间导数算符
,将算符A看作
,再利用
;第二法是计算 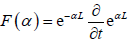 (最终令
)。此外,我们还有两种计算规范势算符
的方法,即(第三法)采用按部就班法(不借助任何技巧),只要把
中的
与
各自
(最终令
)。此外,我们还有两种计算规范势算符
的方法,即(第三法)采用按部就班法(不借助任何技巧),只要把
中的
与
各自
利用泰勒级数展开至第四、五项,就可以发现各项规律;还有(第四法)验证法,对于SU(2)群结构的量子系统,可以将么正变换
的指数算符写为
(
为三个泡利矩阵,
为三维空间中的某个单位矢量),那么算符
,
,于是将这些结
果代入规范势算符
,很容易计算下去。总之,对于规范势算符(或几何相联络)
,我们其实有多种计算方法。
Schrödinger方程对于态矢量
而言,它是线性方程。但是对于态矢量
内的各个分量而言,它就不一定也能说是线性的,这是因为在二态和多态体系中,态矢量内诸分量之间有耦合,且态矢量还要满足归一化约束条件
(从一定意义上讲,这种约束条件也代表一种耦合)。所以,线性的Schrödinger方程也可能表现非线性混沌特点,即态矢量对初始数值具有敏感性(微挠能指数发散)。从根本上讲,这种耦合效应,也与不同时刻的哈密顿量不可对易也有关系。确实如此,如上面由Lewis-Riesenfeld不变量方程得到的辅助代数方程
,
就是这样的非线性方程(值得一提的是,即使避用不变量算符方程 [24],仅仅使用Schrödinger方程,也可以得到该组方程。下面一节“对简单系统避用不变量理论和么正变换方法”证明了这个结论)。但这组方程在一定条件下也有定态解,如假设哈密顿量参数
线性(
)且
(常数),那么我们就有解
,
。但是一旦
,情况就复杂,一般没有解析解,需要依靠数值计算。由于量子计算中涉及二态体系的演化,因此这种由于参数演化所带来的非线性效应值得研究。
5. 对简单系统避用不变量理论和么正变换方法
上面我们介绍了一种思路也即使用Lewis-Riesenfeld不变量理论 [24] 以及与不变量有关的么正变换方法 [26] 可以求解含时Schrödinger方程。但是, 实际上这两法并非总是必须。它们是重要的技巧(当然,这样的技巧其实是很有物理含义的,本文也将阐述其不少物理含义)。但是若一位研究者并不熟悉此二法,其实也不影响其研究含时Schrödinger方程,采用按部就班法也可以获得Schrödinger方程的解。我们以二态体系为例子(当然这种观点对多态体系也成立,只是论述与手工推演操作起来比较复杂)。在下面即将介绍的不需要技巧的按部就班法中,由于代数对易关系已经包含在哈密顿量具体形式之内,所以在计算中也不需要使用到哈密顿量李代数对易关系(也就是说,么正变换、Baker-Campbell-Hausdorff公式等都可以避开使用)。我们考虑如下哈密顿量算符
。
这样的哈密顿量可以描述电子和核子自旋磁矩与磁场的相互作用,也可以描述经典光场与二能级原子的耦合以及约瑟夫森超导结电流隧道贯穿效应。如果该哈密顿量内的参数(
、
)不含时, 则它的两个互相正交的本征态是
,
。
这样的本征态很容易从能量本征值(定态Schrödinger方程)
获得,也可以参看关于电子自旋
或磁共振的量子力学教材。可以发现,
,能量本征值为
。但是,当哈密顿
量参数(
、
)不含时,定态Schrödinger方程不再成立,我们需要求解的是含时Schrödinger方程
。此时上面的
不再是Schrödinger方程的解。但是我们可以预测,含时Schrödinger方
程必然是二维列矢量。那么写为什么样的二维列矢量好呢?上面的
已经构成二维列矢量的归一化、正交、完全集,那么模仿
,我们认为含时Schrödinger方程的解可能具有如下结构:
,
。
此结构与前面地
一样。当哈密顿量不含时,那么参数
,
。于是含时Schrödinger方程的通解是
和
的线性叠加
,
其中允许增加各自的含时相位因子
。我们研究其中一个态矢量
。将它代入Schrödinger方程
,
得到
,其中
,
。
于是由上面的Schrödinger方程, 我们得到两个关系
在上面此二方程中,由于每个方程都有实部和虚部,所以实际上这里有四个方程,但只有三个方程是独
立的,因为从Schrödinger方程可以推导出一个数学恒等式
。于是三个独立方程恰好可以获
得三个变量(
、
、
)。
由上面方程组的第一个关系的实部和虚部,我们可以分别得到
上面方程组的第二个关系可以被写为
。
由其虚部可以得到
。此式在上面其实已经获得。上面该方程的实部可以化为
。
将上面已经得到的
代入上式,我们可以得到
,
其中使用了
。
在相位的时间变化率
中,
。那么相位的时间变化率最终可以化为
,
其中采用了
。利用前面方程
,我们可以得到
。还可以计算得到哈密顿量
和
的期待值
,
。
上面我们证明,即使不使用Lewis-Riesenfeld不变量理论 [24] 以及与不变量有关的么正变换方法 [26],我们使用传统的按部就班法、不采用任何技巧,也是可以把含时Schrödinger方程求解出来的,而且在数学计算步骤上,并不比使用Lewis-Riesenfeld不变量理论以及与不变量有关的么正变换方法时增加复杂性。如此说来,Lewis-Riesenfeld不变量理论以及与不变量有关的么正变换方法是可以避免使用的。上面尽管仅仅讨论了二态(或二能级)体系,其实也是可以推广到三态(或三能级)体系的。
例如我们研究一个哈密顿量算符具有SU(3)李代数结构的量子体系(譬如包含三能级原子与两个或三个经典光场的相互作用体系)。此哈密顿量是八个盖尔曼矩阵的线性叠加。关键是要先构造定态Schrödinger方程的三个三维本征列矢量,然后通过类似
,
等的替换,获得含时Schrödinger方程的解,推导出
、
等所满足的方程。最简单的方法是假设三维本征列矢量是
,把它作为八个盖尔曼矩阵的线性叠加后的哈密顿量本征态,于是获得a、b、c之间的关系。采用参数化方法,a、b、c含有实部和虚部,从表面上看,有六个参量,但是因为归一化原因,实际上只有五个参量。那么从含时Schrödinger方程的角度看,独立的方程也是五个,因为从Schrödinger方程可以推导出一个
数学恒等式
。我们分析认为,即使不采用Lewis-Riesenfeld不变量理论以及么正变换方法,
采用传统的按部就班法,并不增加数学复杂性。所以不变量理论方法与么正变换方法并非研究含时量子系统的必须, 即使研究者不熟悉、不了解此二法, 也不影响研究。
对于哈密顿量具有SU(3)李代数结构的量子体系,它的态矢量可以是如下三个正交归一的基矢量的线性叠加:
,
,
。
当然三维正交归一的基矢量还可以被写为其它形式。对于哈密顿量具有SU(4)李代数结构的量子体系其正交归一的基矢量可以依次类推写出。再在以上基矢量上加相位因子,代入含时Schrödinger方程,就可以得到以上参数
与哈密顿量中的含时参数之间的关系,相位的表达式也可以获得。如此说来, 即使不采用Lewis-Riesenfeld不变量理论和么正变换方法,采用朴素方法,也是可以求解含时Schrödinger方程的,且运算步骤其实也并不增加。在么正变换方法中,需要利用哈密顿量内的李代数生成元的对易关系,而在这里采用的是生成元的具体的矩阵表示,因而可以回避这些对易关系(这些对易关系不必直接使用到)。
6. 不变量理论和么正变换的物理含义
前面提到,Lewis-Riesenfeld不变量理论 [24] 和么正变换方法 [26] 这个体系有很多物理意义。下面将说明这一点。Lewis-Riesenfeld不变量理论和么正变换方法与时空的微分几何具有类比或对应关系。这些类比关系包括:(i) Lewis-Riesenfeld不变量算符I好比弯曲时空度规
,经过么正变换后的不变量算符
好比平直时空度规
。Lewis-Riesenfeld不变量算符有本征值方程,我们将它写为
,这类似
。
类似
(
对应标架场
,V对应标架场
。
与
互为复数共轭)。由此看出,么正变换算符V类比于标架场(vierbein)
。(ii) Lewis-Riesenfeld不变量方程
类比于度规的metricity条件
的展开
。从这个角
度看,Levi-Civita联络
类比于哈密顿量算符H。(iii) 哈密顿量算符H经过么正变换后变为
,可以看出
类比于自旋仿射联络(洛伦兹联络)
,它的具体展开式子是
。(iv)
可以化为
或
,此式其实类比于标架场(vierbein)
的协变导数为
零(
),其展开式为
。值得专门指出的是,严格说来,
对应
,V对应
。
与
互为复数共轭,但是在实数时空和实厄密度规约定下,
与
在数值上相等(都是实数),不必互为复数共轭。如果选定度规可为复数(复厄密度规,即
),那么
与
互为复数共轭,于是上面类比关系可以写为具有完全一样的结构。如此类比很有启发性,但限于篇幅,此专题不再详细写出。
我们已经证明如下形式的
与
,
是不变量算符的本征态,它们满足
。
这是完备性条件。其中
。
又因为不变量算符可以写为
,
现在可以看出,
。又可以计算
,得到
。
我们也可以看出,
。所以,无论是
还是
,它们
其实都是不变量。它们相加,得到的量也是不变量(
);它们相减,得到的量也是不变量(
)。由此说明,不变量其实可以有很多个(在文献 [26] 中还提到构造不变量的方法,以及证明两个不变量的乘积仍旧是不变量)。但只有
才是我们要的不变量(与不变量有关的幺正变换 [26] 中的Lewis-Riesenfeld不变量)。
下面我们来研究另一个重要问题:哈密顿量参数空间的标架场vielbein与度规(包括平直与弯曲度规)。我们发现,
与
可以构成标架场
,
与
可以构成另一个共轭的标架场
:
,
。
也就是说两个vielbein可以写为
,
。
那么不变量算符内部空间度规
可以写为
。
平直度规为
。
从上面看出,
和
都是单位矩阵。实际上这是因为我们选择的vielbein让内部空间(规范群空间)是平直的。我们也可以选择其它更为广义的vielbein让内部空间是弯曲的,这就导致Levi-Civita联络。例如,我们采用
与
作为构造vielbein的素材,然后可以得到弯曲度规
。这里c和s是含时的,而
是Schrödinger方程的相位。在这样的背景下,非阿贝尔内空间的度规
不再平直,因此我们可以计算复Levi-Civita联络和复空间中的黎曼曲率张量。这将在下篇中讨论。
我们在上面已经定义了标架场
、
,由此可以直接写出所谓的“自旋(仿射)联络”
以及对应的曲率张量
(Yang-Mills规范场)。这个“自
旋(仿射)联络”
是前面几何相联络
的推广。如果所研究的系统除了有时间上的
发展参数外,还有空间上的发展参数(如运动的二能级原子在电磁场中),那么就需要使用上述“自旋(仿射)联络”
。系统得到的相位就来自曲率张量
的“磁”通量。
根据Lewis-Riesenfeld不变量理论, 我们应当可以写下如下式子
,
。
于是我们得到
。这样,
,
就是一个与单位矩阵成正比的算符(平庸)。但是,实际上并不总是如此。我们选定
,
。
我们计算得到
。
实际上,这个结果并不稀奇,它其实就是
这意味着
是不变量算符I的属于本征值+1/2的本征态,
是不变量算符I的属于本征值−1/2的本征态。
7. 有关几何相位的讨论
我们再讨论几个与几何相位有关的问题:绝热近似、含时Schrödinger方程的解的幺正变换、不变量与哈密顿量的关系、有几何相位的体系的特征等。
1) 所谓绝热(绝热近似、绝热条件),对一个二态体系而言,就是指它的哈密顿量算符内的演化参数如
(哈密顿量在参数空间内的进动频率)远远小于
(二态跃迁频率) [9] [10] [11],那么我们就有
。所以,在绝热情形的例子中,量子系统的哈密顿量算符
与Lewis-Riesenfeld不变量算符
[24] 是十分接近的、几乎相等的(因此我们可以用量子系统的哈密顿量算符
代替不变量算符
,也就是说,
可以近似允许有瞬时本征态,那么自然Lewis-Riesenfeld不变量算符
也就不再需要了) [26]。但是,对于非绝热情形,哈密顿量
与不变量算符
相差太大 [26],不变量算符
有本征态,但哈密顿量算符
没有(瞬时)本征态(即认为“哈密顿量
有瞬时本征态”的观点是错误的,这是因为如果有瞬时本征态,那么这就与含时Schrödinger方程相悖) [9] [10] [11] [26] [27] [28]。还有一种情形也值得考虑:那就是哈密顿量中耦合项比较小,即
接近于零。此时从不变量辅助方程可以看出,
、
,
。
如果哈密顿量携带含时谐振荡因子,我们总可以通过一个幺正变换,将哈密顿量变为不含时的哈密顿量算符。此时,不变量也可以由含时变为不含时。这种情形就不再属于是绝热条件的问题了,它是一种在根本上就可以化为定态系统的情形。
2) 下面讨论一下含时Schrödinger方程的解的幺正变换(规范变换):
如果
已经是含时Schrödinger方程的解,满足
,
我们来看一个幺正变换:
。我们设
也满足Schrödinger方程,那么么正变换结果如下
。
它可以进一步化为如下形式:
。
我们希望结果等于
。下面我们来得到
:
,
。
所以,
(
为常数相位,但常数相位是没有什么意义的)。我们发现,如果幺正变换算符
本身不携带相位因子的话,在这样的幺正变换下,Schrödinger方程的解的相位本身是不变的。
3) 下面我们来研究SU(2)含时三生成元体系的不变量算符与哈密顿量算符的数学关系(相关的性质可能在一些文献内已经有隐现或交代 [2] [24] [26] [27] [28] ),这可以让读者进一步理解不变量算符和哈密顿量算符之间的依赖关系。Lewis-Riesenfeld不变量算符和量子系统的哈密顿量算符的生成元系数各自可以写为三维空间的单位矢量
和
形式,即
,
。
于是不变量和哈密顿量算符可以各自写成以上单位矢量
和
与由SU(2)三个生成元构成的矩阵矢量的点乘。设哈密顿量
与不变量算符
的矢量系数之间的夹角是
,那么可以证明:
。这只要计算
在
上的投影就可以了:
。
在与不变量有关的幺正变换方法中,经幺正变换之后的哈密顿量是
,
其中
这部分与动力学相位有关,它恰好等于上面已经计算得到的
在
上的投影
。这说明似乎动力学相位被分离出了一部分(因为投影
),哈密顿量在相位上的贡献只是它在不变量算符上的投影。只有在不含时系统中,Lewis-Riesenfeld不变量算符与哈密顿量算符才同一(
),此时没有几何相位,才有
(或者说,此时不需Lewis-Riesenfeld不变量算符)。
4) 什么样的量子系统含有几何相位呢?当然,含时系统含有几何相位。但并非所有含时系统都含有几何相位,根据分析,必须要排除两种情形:(1) 不同时刻的哈密顿量对易的系统。这样的系统其哈密顿量只能是这样的形式:
,其中参量
和
不含时,仅仅
含时。从Lewis-Riesenfeld不变量辅助方程可以看出,
,
,参量
和
不含时,那么
与
也为常数(
、
),这样几何相位(
的时间积分)为零;(2) 哈密顿量中的非对角项(与
与 有关的项)含有时谐振荡因子,其可以通过幺正变换,将时谐振荡因子变换掉(这在上面已经有论证)。此外,为了几何相位是可测相位,还要求哈密顿量(与不变量)满足循回条件(
,
) [2] [26]。在绝热条件下,
与
是等价的。但在非绝热条件下,
比
更基本、更重要 [2] [26]。这一点从与不变量 [24] 有关的幺正变换方法 [26] 得到的新哈密顿量(可以直接用于计算几何相位)
有关的项)含有时谐振荡因子,其可以通过幺正变换,将时谐振荡因子变换掉(这在上面已经有论证)。此外,为了几何相位是可测相位,还要求哈密顿量(与不变量)满足循回条件(
,
) [2] [26]。在绝热条件下,
与
是等价的。但在非绝热条件下,
比
更基本、更重要 [2] [26]。这一点从与不变量 [24] 有关的幺正变换方法 [26] 得到的新哈密顿量(可以直接用于计算几何相位)
就可以发现,循回周期
是直接与不变量的参数有关的。如果没有循回条件,这样的几何相位在数值上不确定。既然具有不定性,就谈不上有物理含义了(也就是说,我们可以通过幺正变换来改变其数值。这是显然的,因为规范变换可以改变“磁”矢量势,如
),但是一旦附上了哈密顿量参数的循回(循环)条件,量子系统的几何相位就被确定了,因为规范变换变不了“磁”矢量势在闭合路径积分下的积分值 [2] [9] [10] [11] [26] (在这里,
的闭合环路积分为零。
与
的闭合环路积分相等,即规范变换改变不了磁通量数值)。由此,难道说非循回条件下的相位(如Lewis-Riesenfeld相位) [24] 就没有物理意义了吗?从是否可测角度讲,它确实是没有物理意义。因为相位的测量一般需要用到干涉条件,而一旦发生了干涉,就必然意味着有闭合环路。所以,可测的相位必须是闭合路径下的相位累积(它是一个相对相位)。绝对的相位是没有(测量)意义的。但是毕竟Lewis-Riesenfeld相位它也是波动方程的解的一部分,从这个角度讲,不能完全说它没有意义。
在几何相联络
中,在对
进行一个循回周期积分后,得到一个立体角
,
即几何相位具有参数空间内的立体角的上学形式。Berry相位(它是绝热循回几何相位) [9] 和Aharonov-Anadan相位(非绝热循回几何相位) [29],就是这样的具有立体角形式的几何相位。Lewis-Riesenfeld相位 [24] 因为其积分区间并非巡回,故不一定能写成立体角形式,但是
是一个立体角微元。作为一个微元,总之既然它也是一个立体角,因而我们认为它也是具有拓扑特征的。因此,Lewis-Riesenfeld相位也可以当作是几何相位(当然,这是一家之言。也有人可能持不同意见)。
8. 本专题的衍伸意义
上面已经提到,使用Gao等人的么正变换方法,新的哈密顿量变为
[26],其中
具有联络(规范势)的特征。在基本相互作用中,我们所熟悉的联络只有两个:规范势(联
络)
(包括四维电磁势和Yang-Mills规范势)和引力理论中的Levi-Civita联络。此外,还有自旋仿射联络(即Lorentz联络,包括其矢量表示和旋量表示),它与引力理论中的Levi-Civita联络有一些联系,将在第二篇中涉及。论及联络,就不得不提一下度规(或标架场vierbein)。在四维时空中“标架场”的德语写法为vierbein (four legs),在大于四维的时空中,标架场写为vielbein (many legs)。实际上,根据与自旋联
络
的类比,我们可以知道
中的么正变换
就是一种“标架场”。引力理论中
的标架场
与四维时空度规
的关系是:
。标架场
所起的作用,是从局域平直Minkowski时空到弯曲的Einstein时空之间的变换。上面的么正变换
,所起的作用也是从不含时的物理
量到含时的物理量之间的变换。两者具有类似功能。自然,类似几何相联络
,普通的Yang-Mills
规范势自然也可以用所谓的Yang-Mills vielbein类似地写出来。而在引力理论的Levi-Civita联络中,代替标架场vierbein的是度规(标架场其实是度规这个矩阵的“平方根”),这一点非常特殊。如Levi-Civita
联络为
[62],按照类似几何相位联络
的形式,Levi-Civita联络只需要包含
这一项即可。但是由于
内指标
与
、
之间具平等关系(处于同一空间),不像几何相位联络
中
的内空间指标(或某种“同位旋”空间指标)与时间指标(外时空指标)那
样并不处于同一空间,因而Levi-Civita联络与几何相位联络在数学结构上相差较大。但是值得一提的是,在广义坐标变换下,Levi-Civita联络也满足与规范变换具有一样数学结构的变换 [62]。它们虽然不是在形式上相似,但是在更加基本层面上享有同一精神。值得顺便提及的是,与Yang-Mills规范势更接近的引力理论中的对应客体是自旋仿射联络。在引力-规范统一理论中,高维自旋仿射联络
就是Yang-Mills规范势。
联络(规范势)导致曲率。在电磁理论中,这就是场强(尤其是磁场)。在非阿贝尔规范理论中,这就是Yang-Mills场强(规范场张量);在引力理论中,这是黎曼曲率张量。在引力-规范统一理论中,与高维自旋仿射联络对应的曲率
就是Yang-Mills曲率(规范场张量、场强)。
自旋联络规范场张量
与黎曼曲率张量之间有关系。我们定义前者如下:
,其中
,最终得到自旋联络规范场张量
。另一方面,使用标架场的协变导数为零(
)这一要求,上面的定义可以变为
,其中左边为
(
为黎曼曲率张量)。将以上两式右边作比较,我们就得到了自旋联络规范场张量
与黎曼曲率张量
之间的关系:
。这一关系颇让人有所启发:由
,我们可以得到自旋联络
,但这里要注意:
是Levi-Civita联络协变导数算符。如果假设Levi-Civita联络为零(要么是全局为零,即恒为零;要么局域为零,即只在局域惯性系内为零),那么上面自旋联络将退化为
以及
。但是,这样一来,由
仍旧可以得到正确的自旋联络规范场张量
,似乎当我们假设Levi-Civita联络为零,并不导致麻烦。其实不然,如果Levi-Civita联络全局为零,那么黎曼曲率张量
恒为零,这样一来上面的关系
就不再成立(左边非零,右边为零),导致矛盾。那么问题出在哪里呢?原来只要存在自旋联络规范场张量
,黎曼曲率张量也必须存在。虽然可以假设Levi-Civita联络局域为零,即只在局域惯性系内为零,但是Levi-Civita联络的导数必不为零(对应于潮汐力即引力落差必然存在)。例如,在
内,有
,在它里面,自旋联络携带有Levi-Civita联络,即使它局域为零,但是其导数却不为零,最终要求黎曼曲率张量也必须存在。如此说来,一旦存在自旋联络或者Yang-Mills场(Yang-Mills场是高维Lorentz转动群规范场),其内黎曼曲率张量就为非零,如高维空间(也即Yang-Mills规范群空间)必须是弯曲的。所以,最终要求自旋联络(Lorentz转动对称性联
络)
才是正确的,而
是错误的。但是在几何相联络
中,关于时
间的导数,为何这里出现的是普通导数算符,而非协变导数算符
呢?原因在于这里复数Levi-Civita联
络
被隐去了,其实它是可以显示出来的。证明如下:我们从Schrödinger方程
出发,将其化为
。再展开为
,
它也就被化为Schrödinger方程的新形式
。
于是新的哈密顿量为
。此推导无错,但是不协变。其实,我们可以在导数上添加一
个复数Levi-Civita联络
,让其具有Levi-Civita联络下的协变性。注意上面我们使用了
,但是实际上此式也可以写为
。
于是我们就可以得到Schrödinger方程的新形式
。
新的哈密顿量为
。这样,真正的几何相联络应当是
(它含有复数Levi-Civita联络
)。外时空中可以取平直(总存在一个局域惯性系),那么复数Levi-Civita联络
可以被设置为零(但是由于“潮汐力”的存在,其普通时空导数不一定为零)。同时,我们关心的是内空间规范群(在引力-规范统一理论中,内空间就是高维空间),外部空间的曲率不会被涉及,所以,复数Levi-Civita联络
可以一直被设置为零而不出矛盾。如此,几何相联络
也是正确的。
上面已经提到,度规或标架场具有上面么正变换
的功能,而Levi-Civita联络才是规范势。但是,不得不顺便提及的是,由于Einstein-Hilbert广义相对论引力理论的微妙性,出现了一种“撞车”现象。度规在广义坐标变换下,却有类似电磁规范势(四维电磁势)的特性(磁矢量势
的规范变换是
,即
,而度规的变换是
。两者在数学形式上很相似),而Levi-Civita联络(本是联络)却在弱场近似下具有引力电场、引力磁场的特点 [62]。与此有关联的是,Einstein-Hilbert引力作用量密度仅仅是一个Ricci曲率标量(而非Ricci曲率标量的平方),而电磁(以及Yang-Mills)规范场的Lagrange作用量密度却是曲率(电磁场强或电磁场张量)的平方。在以联络为宗的前提下,这导致Maxwell电磁理论、Yang-Mills规范理论与广义相对论在数学结构上大不相同。但是,以度规为宗,广义相对论方程在弱场近似下又具有Maxwell方程的结构。所以关于引力场–规范场的统一理论,这就导致两派方案:以联络为宗的引力-规范理论和以度规为宗的Kaluza-Klein理论 [63]。前者的引力作用量密度具有Maxwell-Yang-Mills曲率平方结构(极其推广),要用该结构把Einstein广义相对论引力理论囊括进去;后者的引力作用量密度仍旧具有Einstein-Hilbert曲率标量结构,要把Maxwell-Yang-Mills规范场方程囊括进去。可以说,这是两条相反的路线。两条路线的共同点是:都要引入高维内空间,在引力场框架内将引力场与规范场统一起来,也即Maxwell-Yang-Mills规范场只是高维引力在普通的四维时空内的投影。
9. 结论
微分几何的应用范围不仅仅被限制在数学内,在与数学看起来没有直接关联的其它学科也有其应用范围。例如微分几何在机械力学中也有应用意义(由于机械部件的密度分布不均匀,欧几里德几何距离等概念已经不再直接适用,需要考虑含有弯曲度规、联络、协变导数的微分几何概念,才能方便描述)。此文所阐述的概念、方法可能也可用于理解和研究诸如经典电磁光学(如耦合波导、各向异性晶体光学)、量子光学(光–原子相互作用)、约束体系量子力学、规范场论、广义相对论、引力–规范统一场论以及其它更广泛的专题如金融物理学(涉及规范理论与路径积分技术在量子金融物理学中的应用)等。例如,光场与三能级原子的相互作用,会出现电磁感应透明等与原子能级跃迁路径有关的量子相干(相消干涉)效应 [64] [65]。很多人曾研究了三、四能级原子系统在控制光打开与关闭时的原子系统极化率的瞬态演化效应 [66] [67] [68],这对分析光信息在原子能级中的量子相干存储机制很有价值。这也是一个含时演化过程,相互作用哈密顿量含时间演化参数。量子相干性与相干保持 [69] [70] 在量子计算中十分关键,因此研究人员利用二能级与多模场的相互作用的原子约化密度矩阵方法,研究置于热库中的二能级体系,可以通过外加适当的驱动场,使之满足一定条件,让原子态函数(或状态矢量)保持相干性 [69] [70],这也是一种延迟量子位qubit的量子退相干的很好的思路(这些思路中所包含的情形包括 [70]:热库辐射场与原子之间的大失谐相互作用的二能级体系、具低温热运动的二能级原子系统、线性离子阱中被囚禁的粒子在热辐射驻波场中的运动问题、电场驱动下的简并双光子和多光子过程等。这些研究可见文献 [70] 以及它章末的其它引文)。在这类“相干保持”方案中,由于脉冲或有关驱动场也可能是含时的,那么也值得研究其中的参数演化和几何相位问题。在三能级Lambda位型系统的“电磁感应透明”现象中,两个低能级会线性组合,得到两个正交的暗态与亮态 [64] [65]。其中暗态不与探针光与控制光发生净相互作用,因为它与第三能级(高能级)之间的跃迁电偶极矩的矩阵元为零。与此类似,根据粒子物理学的Cabibbo理论,d和s夸克会线性混合得到新的夸克态(d'和s'夸克) [71],它们也类似暗态与亮态,因此会发生类似“电磁感应透明”中的与原子能级跃迁类似的量子相消干涉机制 [72]。相消、相加量子干涉在基本物理学系统中屡有呈现,包括超导库伯对以及约瑟夫森隧道效应等(在这些宏观量子现象内量子干涉都有其身影隐现)。这方面课题中的量子演化系统效应值得分析。除了这些基本问题外,量子演化系统效应在其它应用型专题如量子计算 [44] [50]、光的自旋Hall效应 [73] 和光学轨道角动量 [74] [75] [76] 等因为存在“等效磁场”的进动因而也有所呈现。
本文根据已有文献介绍了若干研究量子演化系统的理论方法如不变量方法 [24] 和与此有关的么正变换方法 [26],也给出了回避使用此二法的方法。在此基础上,对不变量和么正变换的物理意义作了探讨,发现不变量本征态可以用于构造所谓的标架场,而求解Schrödinger方程的么正变换算符 [26] 正相当于这样的标架场。由此几何相联络的规范群空间内的度规和联络(包括复Levi-Civita和“自旋仿射联络”)都可以分别定义,此二种联络的曲率张量也可以定义。以上这些概念与Berry联络和几何相位都有密切关系,或者说是它们的推广。本文的讨论还不够系统和完整(如度规和标架场的选取还比较特殊,导致规范群内空间仍旧是一个平直空间,度规是平直的。实际上它既然有规范场,因此必须是一个弯曲空间,但这也是可以做到的,这需要推广标架场),但希望对读者有一定的参考意义,以及可以用于研究有关问题,如广义相对论引力场论、微分几何 [5] [6] [77] [78] [79] [80] 及其子问题如Finsler几何 [80] 和复流形 [81] 等(这只是一个愿景,并非一定奏效)。
关于Berry相位、含时演化系统以及几何效应等诸问题,除了外文文献外,前人中文文献如 [2] [6] [11] [26] [27] [28] [51] 已经有独到或精辟或具启发性的解释。本文在这些文献启示下,挂一漏万阐述了其部分要旨;本文前半部分所用不变量计算方法要旨基于文献 [24] [26] 等;本文后半部分(如不变量及其么正变换的物理含义,包括与标架场联系起来,并由此构造参数空间的度规和“自旋联络”以及对应的曲率,将几何相联络以及Yang-Mills规范势,看作是高维内空间“自旋联络”即高维Lorentz转动对称性下的规范势,由此可以进行引力–规范统一等,包括下篇还将论述的一些问题),则属于笔者的一些思考总结。进一步的专题如有关标架场、自旋联络、旋量与挠率等的讨论(以及伴随的度规和曲率张量内容),将在下篇研究。