宇宙质量缺失的一种理论猜想

A Theoretical Conjecture about the Lack of Mass in the Universe

摘要: 通过遥远天体的运动、引力透镜效应、宇宙的大尺度结构的形成、微波背景辐射等观测结果表明，如果基于现有理论计算，宇宙中的星系、星系团等普遍存在“质量缺失”现象，如果不引入额外的质量，将无法对此进行合理解释，这种引入的额外质量就是暗物质。除了引入暗物质，还有另一种方法就是修改现有引力理论，本文不引入暗物质，本质上也没有对现有引力理论进行修改，而是基于观测结果引入一个假设，尝试以另一种全新的角度，对宇宙中普遍存在的“质量缺失”现象进行一种理论解释。

Abstract: Through the observations of distant celestial bodies, gravitational lens effects, the formation of large-scale structures of the universe, and microwave background radiation, it is shown that if the existing theoretical calculations, galaxies and galaxies in the universe generally have the phenomenon of “loss of quality”. Without the introduction of additional mass, this will not be reasonably explained, and the extra quality introduced is dark matter. In addition to the introduction of dark matter, there is another way to modify the existing gravitational theory. This article does not introduce dark matter. In essence, it does not modify the existing gravitational theory. Instead, it introduces a hypothesis based on observations and tries another novel. We try to make a theoretical explanation for the phenomenon of “loss of quality” that prevails in the universe from another new perspective.

1. 引言

1932年，美国加州工学院的瑞士天文学家弗里兹•扎维奇观测漩涡星系旋转速度时，发现星系外侧的旋转速度比牛顿万有引力理论预期的快，因此推测必有数量庞大的质量拉住星系外侧组成，以使其不致因过大的离心力而脱离星系。这个庞大的质量就是后来科学家命名出来的暗物质。后面经过大量的天文观测结果表明，宇宙中所观测到的星系、星系团普遍存在这种“质量缺失”现象。本文不引入暗物质，本质上也没有对现有引力理论进行修改，而是基于观测结果引入一个假设，尝试以另一种全新的角度，对宇宙中普遍存在的“质量缺失”现象进行一种理论解释。

2. 基于现有引力理论和天文观测结果引入假设

我们假设宇宙中有一个河外星系A (椭圆星系或者旋涡星系)，在地球上有一个观测者，通过椭圆星系的位力平衡方法或者旋涡星系的转动曲线方法，得到的星系A总体的动力学质量近似为 $M_1$，通过光学方法比如探测物质的电磁辐射强度，观测者得到的星系A总体的光度质量近似为 $M_2$，经过比较，观测者发现星系A的动力学质量和光度质量明显不等，因为动力学质量是基于理论计算出，所以可以认为是理论质量，光度质量是基于光学方法得到，可以认为是实际质量，所以观测者发现：

$M_1\left(理论质量\right)>M_2\left(实际质量\right)$ (1)

以上结果是依据星系动力学方法得到的，对于引力透镜情形可以得到类似的结果。在实际情况中发现，对于其它星系、星系团普遍存在这种结果。对于这样的结果，一般认为有以下两种解决办法：

1. 修改现有引力理论，使得动力学质量和光度质量大致相等。

2. 星系A中存在看不见的物质质量 $M_3$，使得 $M_2+M_3\approx M_1$。

第一种解决办法实际上是认为所得到的动力学质量有问题，需要对现有引力理论进行修改。修改的引力理论非常多，著名的有MOND理论(相对论版本)、引力的熵力假说、标量-张量-矢量引力理论等。因为牛顿万有引力公式可以由爱因斯坦广义相对论低速弱场近似下得到，所以修改现有引力理论实际上就是要放弃广义相对论，但是从广义相对论诞生开始，到现在随着天文观测技术的发展，科学家们已经对广义相对论进行了一次又一次精确的验证，其中不仅包括在太阳系空间内进行验证，还包括在银河系外更大的宇宙尺度上和更强的引力场情形下，特别是在2016年引力波的发现，至此广义相对论通过了全部检验，是目前最成功的引力理论，所以我们有理由相信，现有引力理论很大可能不会有问题。

第二种解决办法实际上是认为所得到的光度质量有问题，需要引入额外的看不见的暗物质质量。引入的暗物质可分为“重子暗物质”与“非重子暗物质”。“重子暗物质”包括各种死亡恒星、中子星、黑洞等“大质量致密晕天体”以及高度电离的氢氦离子气体等。“非重子暗物质”主要指大质量弱相互作用粒子WIMPs，例如超对称粒子、惰性中微子、轴子等。目前“重子暗物质”已经被排除，所以这里的暗物质主要指“非重子暗物质”。暗物质粒子的探测搜寻实验很多，其中一些已经以失败告终 [1]，一些还在进行中，总之直到目前为止，在差不多100年的时间里，我们并没有能直接发现暗物质粒子的存在。

现有引力理论似乎没有太大问题，暗物质粒子探测实验又一直没有结果，基于这样的状况，其实已经预示着第三种解决办法。

在前面的例子中，我们注意到河外星系A是处于距离太阳系以外遥远的宇宙空间中，对于它的理论质量 $M_1$ 是根据理论计算间接得到的，所以理论质量 $M_1$ 可以认为是太阳系外空间得到的质量，可以表示为：

$M_1\left(理论质量\right)=M_1\left(太阳系外空间得到的质量\right)$ (2)

而光度质量 $M_2$ 是实实在在存在的质量，是观测者在太阳系内空间通过光学方法观测得到的，所以可以认为是太阳系内空间得到的质量，可以表示为：

$M_2\left(实际质量\right)=M_2\left(太阳系内空间得到的质量\right)$ (3)

根据以上关系(1)、(2)、(3)我们可以得到：

$M_1\left(太阳系外空间得到的质量\right)>M_2\left(太阳系内空间得到的质量\right)$ (4)

基于大量暗物质粒子探测搜寻实验结果，我们至少目前为止还不能直接发现暗物质粒子的存在，所以这里我们可以暂且假定暗物质不参与进来，所以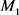和 $M_2$ 实际上是相同的物质质量M，代入式子(4)，我们可以得到：

$M\left(太阳系外空间得到的质量\right)>M\left(太阳系内空间得到的质量\right)$ (5)

以上式子(5)实际上是基于以下两个基本前提条件得到的：

1) 理论依据：大量关于现有引力理论的检验表明，现有引力理论是正确的，并且适用于太阳系外更遥远广阔的宇宙空间。

2) 实验依据：“质量缺失”现象在宇宙中被证明普遍存在。并且大量关于暗物质粒子的探测搜寻实验中，目前为止我们并没有直接发现暗物质粒子的存在。

也就是说，只要假定暗物质不存在，并且认为现有引力理论是正确的并且在整个宇宙空间都一样(包括引力常数G)，那么我们一定可以推导得到式子(5)这个结论，考虑到结论中必须要存在一个具有物理意义的变量，而结论中唯一具有物理意义的变量是处于不同空间中，所以基于这个结论我们可以得到一个假设：

假设：宇宙空间不是处处都一样的，同一份静止质量在这样的不同空间中得到的静止质量会不同。

以上假设实际上是以理论依据1和实验依据2为基础的。根据式子(5)这个结论，我们把太阳系外空

间得到的质量换成 $m_b$，太阳系内空间得到的质量换成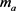，因为 $m_b>m_a$，我们令 $\frac{m_b}{m_a}=k$ (在这里 $k>1$ )，所以：

$m_b=k{m}_a$ (6)

基于以上结果，我们推广到整个宇宙空间，那么我们就可以得到如下公式：

$m\left(k\right)=k{m}_0$ (7)

根据前面的论述，我们知道k只源自于不同的空间，所以本质上和空间有着紧密的联系，如果我们赋予它物理含义，那么k可以看作是空间参数，所以为了便于后面论述，我们暂且称k为空间相对系数，称提出的假设中的不同空间为假设空间。结合相对论质量速度关系，可以推导得到相对论质量也符合以上关系，所以其中 $m_0$ 为太阳系空间内得到的静止质量或相对论质量，m(k)为太阳系外空间相对系数为k的假设空间中得到的静止质量或相对论质量，因为惯性质量等于引力质量，所以这里的质量可以是惯性质量也可以是引力质量。在太阳系空间内，可令k = 1。公式表达的物理含义可以看作是质量和空间的一般关系。

基于公式(7)我们可以得到假设空间中普适的牛顿第二定律公式：

(8)

其中m为太阳系空间内惯性质量，k为空间相对系数，在太阳系空间内，可令k = 1。公式(8)说明：对于同一个物理对象在假设空间中惯性力可能不同。公式表达的物理含义可以看作是惯性力和空间的一般关系。

基于公式(7)我们可以得到假设空间中普适的万有引力公式：

$F\left(k\right)=\frac{G{k}_1{k}_{2}mM}{R^2}$ (9)

其中m、M为太阳系空间内引力质量。 $k_1,k_2$ 分别为两个假设空间的空间相对系数，在同一个空间中， $k_1=k_2$，在太阳系空间内，可令 $k_1=k_2=1$。公式(9)说明：对于同一个物理对象在假设空间中万有引力可能不同。公式表达的物理含义可以看作是引力和空间的一般关系(和广义相对论不冲突)。这里需要说明的是，在同一个空间中我们可以令 $G{k}_1{k}_2=\beta$，即引进一个新常数，由于在不同的假设空间中空间相对系数k不一样，因此引进的常数在不同的假设空间中是变化的，但是这种变化是质量变化导致的有明确物理机制，因此这和前面的理论依据1中，我们假定太阳系空间内引力常数G适用于太阳系外更遥远广阔的宇宙空间并不矛盾。

基于公式(7)我们可以得到假设空间中普适的质能关系式：

$E\left(k\right)=km{c}^2$ (10)

其中k为空间相对系数，在太阳系空间内，可令k = 1。公式(10)说明：对于同一个物理对象在假设空间中静能可能不同。公式表达的物理含义可以看作是能量和空间的一般关系。这样能量、质量、空间通过光速就简单联系了起来，结合能量守恒定律，该公式实际上蕴含着更深刻的物理思想，以此建立的理论模型可以尝试解决很多物理问题，详细探讨需要通过后续进行。

基于公式(7)，我们可以得到假设空间中普适的德布罗意波长公式：

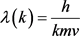(11)

其中k为空间相对系数，在太阳系空间内，可令k = 1。公式(11)说明：对于同一个物理对象在假设空间中德布罗意波长可能不同。公式表达的物理含义可以看作是德布罗意波长和空间的一般关系。

以上推论都是基于公式(7)得到的，实际上只需要把质量代换掉就可以，因为更严格的物理数学推导最后也是会得到这样的结果，所以这里不做详细讨论。需要说明的是，以上所有结论在理论上都是可以和现有物理理论进行融合的，融合的结果就是可以得到其它推论。下面我们再来推导几个结论。

根据公式(11)，在我们太阳系空间内，光子的波长可以表示为：

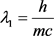(12)

在假设空间中，光子的波长可以表示为：

${\lambda }_2=\frac{h}{kmc}$ (13)

公式(13)说明，在空间相对系数k > 1的空间中，光子的波长相对于太阳系空间内变小了，波长变化为：

$\Delta \lambda ={\lambda }_1-{\lambda }_2=\frac{h\left(k-1\right)}{kmc}$ (14)

因此当k > 1时，在实际的观测中会出现红移。波长变化了频率也会发生变化，在这里光子频率变化可以解释为时钟快慢的变化，因为现代的时钟标准都是基于光的频率来确定的，所以在假设空间中，理论上时间快慢也会发生变化，我们令表示太阳系空间内时间， $t_2$ 表示空间相对系数为k的空间中的时间， $T_1$ 、 $T_2$ 分别表示各自的周期，根据公式(12) (13)最后可以得到：

$\frac{t_1}{t_2}=\frac{T_1}{T_2}=\frac{{\lambda }_1}{{\lambda }_2}=k$ (15)

基于以上结果，我们推广到整个宇宙空间，那么我们就可以得到如下公式：

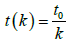(16)

其中 $t_0$ 表示太阳系空间内时间，t(k)表示太阳系外空间相对系数为k的假设空间中的时间，k为空间相对系数，在太阳系空间内，可令k = 1。公式说明，在假设空间中时间快慢可能不同。公式表达的物理含义可以看作是时间和空间的一般关系。

根据以上基本物理公式，还可以得到很多推论，篇幅原因在这里只讨论后面论述需要用到的公式。下面，基于以上结论，我们简单讨论一下“质量缺失”现象这个问题。

3. 基于假设对宇宙中“质量缺失”现象进行论述

3.1. 宇宙大尺度结构的形成

根据宇宙大爆炸膨胀理论，我们现在的宇宙是由一个致密炽热的奇点于137亿年前一次大爆炸后膨胀形成，宇宙大爆炸膨胀理论目前已经有大量证据，这里我们暂且认为它是正确的理论。关于宇宙大尺度结构的形成演化，在现实情况中比较复杂，一般都是通过大型计算机N体数值模拟进行辅助研究，所以下面只进行一些简单的理论基础讨论。

基于宇宙大爆炸膨胀理论，那么本文所提出的假设中的不同空间，理论上必然都存在一个起点，如下图所示：

Figure 1. Set of spatial points

图1. 空间点集合

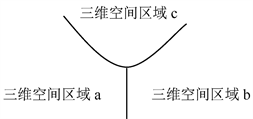
Figure 2. Different space regions formed by space expansion

图2. 空间膨胀形成的不同空间区域

如图1假设宇宙大爆炸后存在三个彼此相邻的空间点集合，并且它们都满足本文所提出的假设空间中的空间属性，随着空间极速膨胀，图1这样的不同空间点集合最后会形成类似图2这样的不同三维空间区域，因为理论上有无数个这样的不同空间点集合，所以基于这样的模型，最后会形成无数个不同三维空间区域，并且这些不同三维空间区域在整体上会呈泡沫状结构分布。

在目前的标准宇宙模型中，一般认为我们今天所看到的宇宙大尺度结构，是源自宇宙早期无碰撞的低速暗物质粒子作用。在这样的模型中，在宇宙早期线性演化阶段，宇宙中主要包含重子、辐射、冷暗物质，在辐射为主时期，它们的密度扰动增长是同步的，直到复合结束，因为冷暗物质的扰动不受光子阻尼影响，因此当重子和辐射脱耦之后重子会在冷暗物质的扰动影响下恢复扰动增长，最后在引力作用下形成现在的宇宙大尺度结构。

没有暗物质就无法形成恒星、星系以及现在所观测到的宇宙大尺度结构，因此任何一个暗物质替代理论，都至少应该能够得到同样的结果。因为这里已经假定了暗物质不存在，所以演化过程会出现一些变化。如下所示：

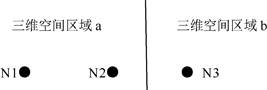
Figure 3. Two different spatial regions

图3. 两个不同空间区域

如图3，我们设想宇宙早期线性演化阶段存在两个相邻的提出的假设中的不同三维空间区域a、b，空间相对系数分别为 $k_1$ 、 $k_2$，我们设想在时间某刻空间区域a中有一个质量为 $m_1$ 的粒子N1和一个质量为 $m_2$ 的粒子N2，空间区域b中有一个质量为 $m_3$ 的粒子N3，并且N1和N3到N2的距离大致一样。由于宇宙早期辐射和某些粒子都是相对论性的，此时不仅要考虑物质和辐射本身的扰动，还要考虑时空度规的扰动，但是这里我们为了便于理解和论述，我们只取理想情形下运用牛顿力学进行简单的理论基础讨论(不影响定性结果)。基于本文提出的假设得到的推论，根据公式(9)有：

1. N2受N1引力为 $F_1=\frac{G{k}_1^2{m}_1{m}_2}{R^2}$ (17)

2. N2受N3引力为 $F_2=\frac{G{k}_1{k}_2{m}_2{m}_3}{R^2}$ (18)

由公式(17) (18)再根据公式(8)可以得到：

1. N2受N1引力加速度 $a_1=\frac{G{k}_1{m}_1}{R^2}$ (19)

2. N2受N3引力加速度 $a_2=\frac{G{k}_2{m}_3}{R^2}$ (20)

由以上公式(19)、(20)可以得到：

$\Delta a=a_2-a_1=\frac{G{k}_2{m}_3}{R^2}-\frac{G{k}_1{m}_1}{R^2}=\frac{G\left(k_2{m}_3-k_1{m}_1\right)}{R^2}$ (21)

因为宇宙早期物质分布均匀，当重子和辐射脱耦之后，这里的 $m_1$ 和 $m_3$ 在整体的随机分布上可以看作是近似相等的，所以当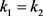时，以上得到的结果整体上是趋于稳定的。当 $k_1\ne k_2$ 时，以上得到的结果整体上是不稳定的，因此在三维空间区域a和三维空间区域b相邻处，那里会产生小尺度上的原初密度扰动，随着引力作用，原初密度扰动会增长，因此物质最先在那里进行聚集，随着宇宙早期空间的急速膨胀，最终这里会形成恒星、星系、星系团、以及星系长城。而因为三维空间区域a和三维空间区域b中间区域的物质在开始时整体上是趋于稳定的，因此那里绝大多数物质最后都被吸引到边缘进行聚集，所以最终那里会形成宇宙空洞。因为宇宙中存在无数个这样的不同空间区域，所以基于这样的模型，理论上会得到一个物质以泡沫状分布的宇宙大尺度结构。如图4所示：

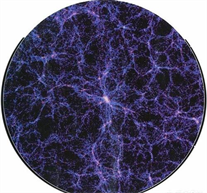
Figure 4. Large scale bubble structure simulation of the universe

图4. 宇宙大尺度泡沫结构模拟

在公式(21)中，我们令 $\Delta k=\left|k_1-k_2\right|$，由于 $\Delta a$ 主要由 $k_1$ 和 $k_2$ 共同进行决定，因此重子原初密度扰动情况主要由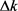进行决定， $\Delta k$ 越大， $\Delta a$ 也越大，所以基于这种演化模型，在理论上可以形成规模非常大的宇宙长城和宇宙超级空洞，比如在2013年发现的延伸超过100亿光年的武仙–北冕座长城，2007年发现的跨度达10亿光年的波江座超空洞，理论上这种巨大超结构在以冷暗物质和宇宙学原理为基础的标准宇宙模型下是很难存在的，可见在这一点上本文所提出的假设比暗物质假设更有优越性。

以上表明，基于本文提出的假设建立的演化模型，我们现在所看到的物质在宇宙大尺度泡沫状结构分布，实际上是宇宙不同空间的泡沫状结构分布，需要说明的是，因为这种不同空间没有绝对界限，所以随着宇宙空间膨胀，最后所得到的同一个空间区域，其空间相对系数k也不一定都是处处相同，只能看作是近似相同，这点可以结合实际天文观测得到的宇宙“质量缺失”分布状况做一些细节上的调整，这在理论上是没问题的。以上例子中只是取理想模型进行简单定性讨论，因为实际上根据公式(16)，我们还必须要考虑时间参数，并且因为宇宙早期辐射和某些粒子都是相对论性的，需要使用广义相对论进行描述，综合这些因素理论描述会变得非常复杂，但是这里简化模型并不影响定性结果。因此以上基于提出的假设关于宇宙大尺度结构的形成演化，可以通过大型计算机N体数值模拟进行更精确的模拟验证。

3.2. 星系、星系团“质量缺失”现象

理想模型下，在漩涡星系中，其中恒星的逃逸速度可以由牛顿力学近似得到：

$V\approx \sqrt{\frac{2GM}{R}}$ (22)

根据前面得到的公式，在空间相对系数为k的假设空间中恒星的逃逸速度近似为：

$V\left(k\right)\approx \sqrt{\frac{2kGM}{R}}$ (23)

根据公式(22) (23)有：

$V\left(k\right)\approx V\sqrt{k}$ (24)

在我们太阳系空间内，可以令k = 1，而当漩涡星系处于k > 1的空间中时，根据公式(24)理论上恒星的逃逸速度可以更大，当然运动速度也可以更大。对于椭圆星系有类似的结果，其中的恒星、气体等速度弥散度可以更大。

以上只是一方面，基于假设以及得到的推论，我们至少还会在以下三个方面会对星系、星系团的质光比估算出现偏差：

1. 恒星表面辐射可以近似看做是黑体辐射，根据公式E = hv和公式(11)，在空间相对系数k > 1的空间中，光的频率更大，因此能量更高，恒星辐射能量也更高，因为我们都是在太阳系空间内对遥远天体进行观测，因此我们接收到的天体发出的光的能量实际上变小了。所以对于一个实际光度为L(k)的天体，我们观测到的光度为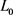，根据光度函数那么可以近似得到：

$L\left(k\right)\approx k{L}_0$ (25)

其中k为空间相对系数。也就是说，在这种情形下，我们最后所得到的遥远天体的光度质量实际上会比真实值偏小。

2. 对于理想漩涡星系，星系转动速度可以用氢原子21厘米光谱线的多普勒频率移动效应来测量,其中恒星或者气体轨道运动引起的多普勒频移可以由以下公式近似表示：

$\frac{\Delta \lambda }{\lambda }\approx \frac{V_r}{C}$ (26)

其中 $\lambda$ 为本征波长， $\Delta \lambda$ 为观测到的频移所产生的波长变化， $V_r$ 为恒星或气体运动速度在观测者视线方向上的投影。我们令 $\Delta {\lambda }_0$ 表示运动导致的多普勒频移波长变化，令 $\Delta {\lambda }_{\mathrm{k}}$ 表示假设空间导致的波长变化，根据公式(14)那么实际上我们在太阳系空间内获取到的 $\Delta \lambda$ 应该为 $\Delta \lambda =\Delta {\lambda }_0+\Delta {\lambda }_k$，我们令V(k)为实际值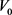，为观测值，根据公式(26)最后可以得到：

$V\left(k\right)\approx V_0\left(\frac{\Delta \lambda -\Delta {\lambda }_k}{\Delta \lambda }\right)$ (27)

根据公式(14)在空间相对系数k > 1的空间中 $\Delta {\lambda }_k>0$。因此我们在太阳系空间内观测得到的运动速度会偏大，也就是说，在这种情形下，我们最后所得到的旋涡星系的动力学质量实际上会比真实值偏大。对于椭圆星系有类似的结果。

3. 恒星质量越大一般寿命越短，在天文学上恒星的寿命和质量一般有如下关系

$t\propto \frac{1}{M^{a-1}}$ (28)

在一个空间相对系数为k的空间中，根据公式(7) (16) (28)其中恒星的寿命和质量可以表示为：

$t\left(k\right)\propto \frac{k}{{\left(kM\right)}^{a-1}}$ (29)

以上两个时间进行比较有：

$\Delta t\propto t-t\left(k\right)\propto \frac{1}{M^{a-1}}-\frac{k}{{\left(kM\right)}^{a-1}}\propto \frac{k\left(k^{\left(a-2\right)}-1\right)}{{\left(kM\right)}^{a-1}}$ (30)

因为k > 1，天文学上规定a > 1，所以 $\Delta t\ge 0$，也就是：

(31)

当a > 2 时 $t>t\left(k\right)$。这说明在空间相对系数k > 1的空间中，其中的恒星寿命可能相对更短，也就是演化可能更快，恒星最后一般都会变成白矮星、黑矮星、中子星、黑洞，这就导致处于空间相对系数k>1的空间中的星系，其中的不可见重子物质可能相对会更多。

当a = 2时 $t\equiv t\left(k\right)$，和空间相对系数k无关。对公式(30)进行数学分析，根据宇宙中大量星系、星系团的质光比进行估算，即使不排除前面讨论到的我们在太阳系空间内得到的质光比实际上偏大这个因素，k的取值普遍情况也不会很高。因此尽管在空间相对系数k > 1的空间中粒子的质量相对更大，但是因为其中的时间相对也变慢了，因此不会出现因为天体演化过快而和现实观测相差太大的情况。

至少存在以上三种情形使我们在太阳系空间内获取得到的星系、星系团质光比比真实值偏大。

实际的观测发现，每个星系、星系团“质量缺失”比例可能是不同的 [2]，也正是这点，才彻底否定了那些试图通过修改引力理论对“质量缺失”现象进行解释的解决办法，因为引力理论应该具有普适性。关于这点，在提出的假设空间中，可以由空间相对系数k的不同情况进行决定：

1. 当k > 1时，理论上可以证明在这种空间中星系、星系团会出现“质量缺失”现象。而且k越大“质量缺失”比例越大。

2. 当k ≈ 1时，理论上可以证明在这种空间中星系、星系团“质量缺失”现象不会很明显。

3. 当k < 1时，理论上可以证明在这种空间中星系、星系团会出现和第一种情况相反的情形。

以上的1、2种情形在实际的天文观测中已经被观测到 [3]，可以和现实相符合。如果我们人类在宇宙中所处的空间不是特殊的，那么基于提出的假设理论上还会存在第3种情形，但是在这种情形中，根据公式(11)和公式E = hv可知：在k越小于1的空间，光的实际波长λ会相对越大，光的能量越低，因此遥远天体光度相对会越小，亮度相对也会越暗，因此在实际的天文观测中可能会很难发现这种情形。

对于星系团引力透镜、宇宙微波背景辐射等“质量缺失”情形，本质上都是类似的，这里不再做详细讨论。

4. 对提出的假设进行初步验证的一种直接方法

根据哈勃定律，星系谱线红移和距离成正比，可以由以下公式表示：

$z\equiv \frac{\Delta \lambda }{{\lambda }_0}=\frac{1}{c}{H}_{0}d$ (32)

其中 $\Delta \lambda$ 表示观测到的谱线波长变化量， ${\lambda }_0$ 表示谱线固有波长， $H_0$ 表示哈勃常数，d表示星系距离。根据公式(14)当k > 1时我们在太阳系空间内获取到的 $\Delta \lambda$ 实际上会偏大(关于星系距离d的测量方法有很多，如果涉及光谱分析最后得到的结果可能也会偏大)，因此这种情况下我们通过观测太阳系外遥远天体测量得到的哈勃常数值，理论上会比我们在太阳系内测量得到的偏大。这种结果在实际的测量中其实早已被发现，被称为“哈勃常数问题”。天文学家发现，基于宇宙微波背景(CMB)辐射进行测量得到的哈勃常数，和通过观测太阳系外遥远天体比如Ia型超新星、类星体等得到的哈勃常数并不一致，基于宇宙微波背景(CMB)辐射进行测量得到的哈勃常数，实际上可以看作是太阳系内空间得到的哈勃常数值，基于太阳系外遥远天体测量得到的哈勃常数，实际上可以看作是太阳系外空间得到的哈勃常数值，两种结果的不一致，是支持本文提出的假设最直接的证据，基于这种推论，后续可以进行数值上更精确的检验。

5. 结语

本文给出了宇宙中“质量缺失”现象的一种理论解决方法。篇幅原因，关于宇宙中的“质量缺失”现象，以上只进行简单的初步定性讨论，对于其它可能存在的一些细节问题，需要通过后续对基于假设建立的模型进行不断调整和完善。关于本文所提出的假设，这里也只进行一些理论基础讨论，对于更仔细深入的研究需要在后续进行。

质量会发生变化在物理学中并不是第一次出现，因为在相对论中就存在运动质量变化这个结论，并且已经得到了实验验证。和相对论中的运动质量变化不同的是，这里假设中的是静止质量变化。下面我们想象一下这样的一个思想实验：

1. 我们取地球作为静止参考系，那么根据狭义相对论，惯性参考系中的运动质量(空间相对系数k = 1的空间中)可以表示为： 。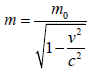

2. 我们取地球作为静止参考系，那么根据本文所提出的假设，在一个空间相对系数为k的空间中，根据公式(7)其中的静止质量可以表示为： $m\left(k\right)=k{m}_0$。

在以上两种情形中，我们假设都处于一个密封的大箱子中，里面存在一个观测者，那么理论上这个观测者将无法区别所得到的变化质量是处于哪种情形下。如果这两种情形下我们令它们得到的质量相等，那么我们可以得到以下关系：

(33)

这样空间相对系数k和洛伦兹因子就联系了起来。我们知道相对论中的运动质量变化会存在着空间变化，在这里假设中的静止质量变化也是因为物质处于不同的空间中，虽然它们的空间变化形式可能不同，但是以上结果似乎表明，也许这两种情形导致的质量变化在物理本质上应该是一样的，因此物理机制上应该可以将它们进行统一，关于这点需要进行更深入的后续研究。巧合的是，这两种情形得到的质量变化结论，有着相似的背景和动机：

1. 麦克斯韦理论 → 得到光速c结果 → 引入以太解释 → 抛弃以太 → 得到运动质量变化结论。

2. 广义相对论 → 得到“质量缺失”结果 → 引入暗物质进行解释 → 抛弃暗物质→ 得到静止质量变化结论。

其中的暗物质和以太非常的类似。这里其实只是想说明，理论上暗物质不参与任何电磁相互作用，所以理论上看不见摸不着，而根据以往情形，难以证伪的东西在物理学中或许都是没必要的。而本文所提出的假设即保留了现有引力理论，也不需要引入额外的奇怪物质，所以根据奥卡姆剃刀原理，在这点上本文所提出的假设比暗物质假设更有利。但是话说回来，对于宇宙中普遍存在的“质量缺失”现象，和其它很多解决办法一样，本文也只是提供另一种解决办法，所有这些解决办法中，也许都是错的，也许有一个是正确的，但是也许还存在两种情况共存的可能性(可以互补缺陷)。科学是严谨的，一切应该要以实际的天文观测证据作为标准，而基于本文所得到的一些推论，可以作为后续的天文观测检验依据。