1. 引言
股市投资作为重要的一种投资方式,已为越来越多的人所关注。随着近些年股市的动荡,人们意识到在追求高收益的同时还伴随着高风险。如何能让“利润充分增长”,而规避掉一定的风险,也就是对股市的预测,包括股价的预测,波动性的预测等等已经成为重要的研究课题之一。近些年来由于受到各方面因素的影响,国内股票市场动荡,几次出现暴跌现象。比如2015年6月19日,大盘表现疲弱,午后跳水,跌幅一度逾6%,相继失守4600、4500点位,两市近千只股票跌停。2017年11月23日,A股低开低走,全线深幅调整。上证综指失守3400点整数位,创下年内最大单日跌幅等等。面对诸如此类股市巨大的波动,传统的GARCH族模型分析结果不尽如人意。我们要对GARCH族模型进一步改进以获得对股票市场更好的分析预测。
2. GARCH族模型的由来及发展
波动率是衡量投资风险程度的重要指标,在金融领域里被定义为收益的标准差。它受到很多因素的影响,比如可能受到的外部因素有:国际形势的稳定,国内经济的发展,国民投资的热情等,内部因素有:股票的股价,日成交额,市盈率等。股票市场的波动问题一直以来都是众多学者研究的课题之一。国外证券市场的发展已有数百年之久,其发展程度已十分成熟,众多学者对股票价格收益率波动的规律进行了深入研究。研究者普遍认为,历史会重演。其基本思想是:根据股市的历史数据建立起波动率模型,再根据建立的模型去预测股市未来的发展趋势。其中最为典型的一类模型就是条件异方差模型。这类模型最早的提出者是美国加州大学圣迭戈分校的Robert F. Engle,他在1982年提出了自回归条件异方差模型(ARCH模型) [1],具体模型如下:
其中,
表示股价收益率序列,
表示股价收益率序列均值,
表示收益率序列残差扰动项,
为收益率序列方差,
与常数成正比,
为系数。
表示滞后一阶的信息。
为标准化残差服从正态分布(本文只考虑正态分布)。ARCH模型的贡献是开创性的,其最大的特点是提出了股价的波动是与之前的波动有关联的,从而提出了股价的波动具有聚集性。但是ARCH在可操作性上仍有欠缺,没有办法解决高阶难以计算问题也不能解释股价在受到正负两种信息冲击下反应出的不对称性,也即我们说的股市中的“杠杆效应”。为了解决上述两个问题,人们又分别提出了GARCH模型 [2] 和T-GARCH模型 [3],其具体形式如下:
其中,
,
是系数,
是关于
的指示变量,即
。GARCH模型和T-GARCH模型的提出很好解决了高阶难计算和股价波动的非对称性。
3. GARCH模型族的改进
GARCH族模型的本质是利用已知的股价波动信息拟合出方程去预测股市未来的波动情况。而在GARCH族模型中用到的信息只有
(与真实值的残差扰动)和
(上一期的预测方差),而没有考虑到影响股价波动的其他内在因素,比如:成交金额,股价极差,交易量等。事实上,很多学者的研究已经表明交易量,交易金额对股市的波动具有显著的影响。夏宁伟、詹海、马锋(2014),先后分别运用深证和上海综合股价指数,沪深300指数,深圳成分指数,证实在中国股票市场中,交易量同样对收益波动率有显著的解释作用,引入交易量的GARCH模型能更好地拟合和预测股票指数的波动性 [4]。而李伶在把交易量引入到GARCH族模型中得到的新的GARCH族模型对股市的分析预测有着比GARCH族模型更好的结果 [5]。本文按照这一思路,将成交金额这一影响因素加入GARCH族模型,得到的改进GARCH模型和改进T-GARCH模型如下:
其中,
是前一天的成交金额。改进后的GARCH模型和T-GARCH模型保持了原有的均值方程不变,在方差方程里加入了
项,这样可以通过观察系数
,
,
的变化,直接可以看到加入成交金额后,成交金额这一影响因子对方差的贡献率,以及对ARCH项和GARCH项的影响效力的改变。
4. 实证分析
本文利用修改过的模型分别对上证指数(000001)和深证成指(399001)作实证分析。上证指数又称上证综指,是上海证券综合指数的简称。其样本股是在上海证券交易所全部上市股票,包括A股和B股,反映了上海证券交易所上市股票价格的变动情况,自1991年7月15日起正式发布,基日定为1990年12月19日,基日指数定为100点。深证成指是深证成份指数的简称,是深圳证券交易所的主要股指,以1994年7月20日为基期,基点为1000点。这两个指数是沪深市场具有代表性的两个指标,所以选取它们来做实证分析。
4.1. 数据选取与处理
本文用到的数据处理软件为Eviews10.0,数据来源为网易财经数据库,因为股市股价会受到股权分期改革等影响,又考虑到时效性的问题,综合多方面考虑,选取上证指数从2016年5月3日到2019年2月28日共689个数据(如图1),选取深证成指从2016年2月29日到2018年2月28日共490个数据进行分析(如图2)。通过查阅大量文献,为保证序列的平稳性,本文采用对数差分的方法来刻画股价的收益率序列(
)和日成交金额序列(
)。即处理后的数据为
(如图3,图4)和
(如图5,图6)。如下图所示。
从下图中我们可以看出两点。一是在上证指数和深证成指中收益率的波动往往呈现出一定的聚集特性,即波动小的地方往往很平稳,波动大的地方往往聚集在一起,这就是波动聚集性。二是我们可以发现当利好消息出现,人们纷纷交易投资,股价上升的趋势远不及当利空消息出现,人们撤资带来的股价下跌的趋势,这就是不对称性,也就是“杠杆效应”。
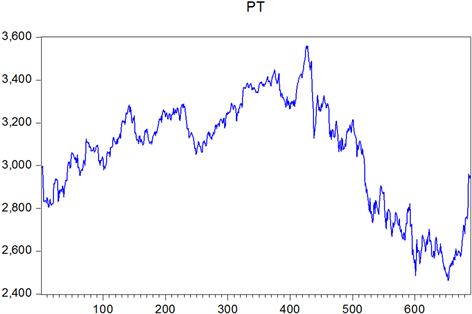
Figure 1. Time series chart of Shanghai stock exchange price
图1. 上证价格时序图

Figure 2. Time series chart of Shenzhen stock exchange price
图2. 深证价格时序图
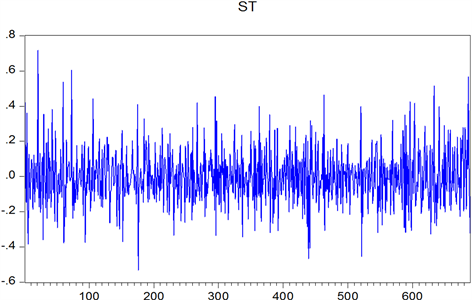
Figure 5. Shanghai stock exchange transaction amount series
图5. 上证成交金额序列
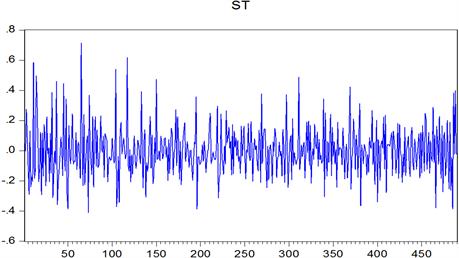
Figure 6. Shenzhen stock exchange transaction amount series
图6. 深证成交金额序列
4.2. 数据的平稳性以及ARCH效应检验
我们分别对所选取的上证数据和深证数据进行平稳性检验和ARCH效应检验。在针对时间序列分析时,要保证数据的平稳性。这是用方程拟合得出结果来预测未来趋势变化的前提条件。一个不平稳的时间序列是无法对未来趋势变化做出合理解释的。在大多数的实证研究中,均采用ADF (Augmented Dickey-Fuller)检验。本文也采用ADF检测上证和深证数据的平稳性,结果如下(见表1):
从上图我们可以看出,各个序列的峰度都高于正态分布的峰度3,都呈现出明显的尖峰厚尾性。各个序列经过ADF检验,得到的伴随概率P值几乎为零,并且ADF值均明显小于1%的临界值,表明数据是平稳的,可以进行下一步ARCH效应的检验。
ARCH是自回归条件异方差的缩写,ARCH效应检验的目的是判断GARCH模型均值方程中残差扰动项平方是否存在自回归的现象,即数据有没有ARCH效应。这是数据能够用GARCH模型族拟合的前提。模型的均值方程为:
,记残差的平方为
,则有:
,下面对
作残差平方Q统计量检验,结果见图7,图8。
由图7,图8所示,滞后10阶的残差平方Q检验图表明其中的自相关和偏自相关系数均不为零,而相应的Q统计量的伴随概率几乎为零,从而拒绝原假设,说明序列具有明显的ARCH效应,可以对数据进行GARCH族模型的拟合。
4.3. 改进GARCH族模型的拟合
有了对数据的平稳性检验和ARCH效应检验,接下来可以对改进的模型进行拟合。前文已经叙述了改进后的GARCH模型和T-GARCH模型,为了方便对比,运用Eviews软件分别对上证指数、深证成指做改进前和改进后的GARCH、T-GARCH模型的拟合,得到的拟合结果如下(见表2)。
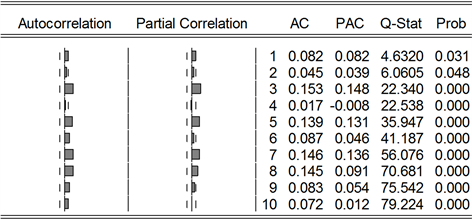
Figure 7. Arch test of Shanghai stock exchange
图7. 上证ARCH检验
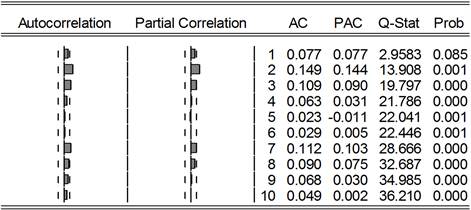
Figure 8. Arch test of Shenzhen stock exchange
图8. 深证ARCH检验
通过观察上图拟合出的方程系数我们可以看出以下几点:1) GARCH项的系数
比常数项
和ARCH项系数
明显要大得多,说明预测的波动率不仅和前一天的真实波动有关,更与之前预测的波动
有关,这也是从数值角度分析出了股市确实存在着波动聚集性。2) 通过观察T-GARCH模型中的系数
,发现其都成正值。这说明股市中负的冲击所造成的影响大于正的冲击所造成的影响,这与我们上述观察到的收益率的波动图像是一致的。3) 两个指数,两种模型,改进后的模型系数
都相较改进前有了明显的降低,这表明改进是有意义的。相当于在加入成交额影响因子后,原来GARCH项的效力减弱了,在有关波动的影响力方面,成交额因子成功分担了一部分,直接体现出成交额确实对股价的波动有着显著的影响。4) AIC (Akaike Information Criterion)信息准则,通过AIC可以说明回归的好坏,所取得的变量使得AIC越小越好。通过拟合得到的改进后的模型不仅可以解释成交额因子对股市波动的贡献率,而且加入成交额因子后,模型AIC较小,相比之前的模型更加优化。
4.4. 改进GARCH族模型对股市波动的预测
现在根据拟合出的GARCH模型和T-GARCH模型对股市的波动进行预测。上证指数的预测区间为2019年3月1日到2019年12月31日共207个数据(实际操作时考虑到迭代初值从2019年2月1日开始迭代)。深证成指的预测区间为2018年3月1日到2019年3月29日共264个预测值(实际从2018年2月开始迭代)。为了能够比较预测能力的好坏,也就是预测值和真实值的差异大小,我们考虑以下两个函数:
和
其中,n代表预测区间的长度,即预测数据的个数,A代表预测值,B代表真实值,这样通过RMSE和MAE我们可以直观地看出预测值与真实值得差异,可以比较出各个模型预测能力的好坏。下面分别用修改前后的GARCH模型和T-GARCH模型对两个指数的波动进行预测,考察预测值与实际值的差异。经计算得到的RMSE和MAE值如下(见表3):

Table 3. Comparison of model prediction ability before and after improvement
表3. 改进前后模型预测能力对比
图中的单位为10−4,通过上图的对比,可以看出无论是上证指数还是深证成指,改进后的模型RMSE值和MAE值都有所下降,表示利用改进后的模型对股市波动的预测值离实际值更接近,预测效果更好。下面是上证指数和深证成指的真实波动率图像(见图9,图10)和利用改进后的GARCH模型和T-GARCH模型对上证指数和深证成指股市波动的预测图像(上证从2019年3月1日至2019年12月31共207个数据(见图11,图12),深证从2018年3月1日到2019年3月29日共264个(见图13,图14)):
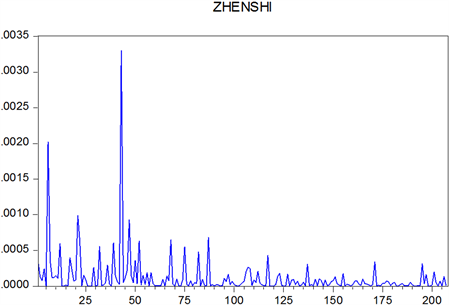
Figure 9. Real volatility of Shanghai Stock Index
图9. 上证指数真实波动率
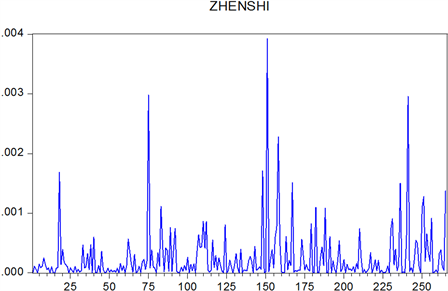
Figure 10. Real volatility of Shenzhen Stock Index
图10. 深证指数真实波动率
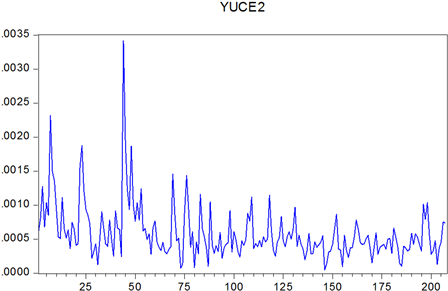
Figure 11. Improving GARCH’s forecast volatility of Shanghai Stock
图11. 改进GARCH上证预测波动率
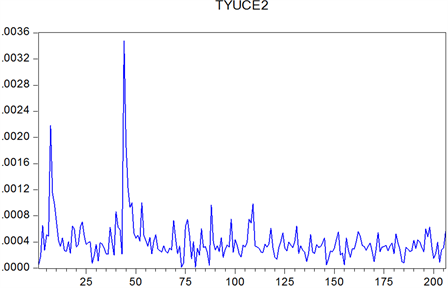
Figure 12. Improving T-GARCH’s forecast volatility of Shanghai Stock
图12. 改进T-GARCH上证预测波动率
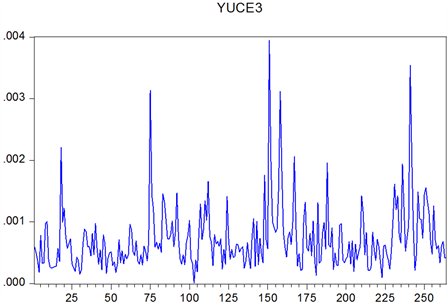
Figure 13. Improving GARCH’s forecast volatility of Shenzhen Stock
图13. 改进GARCH深证预测波动率
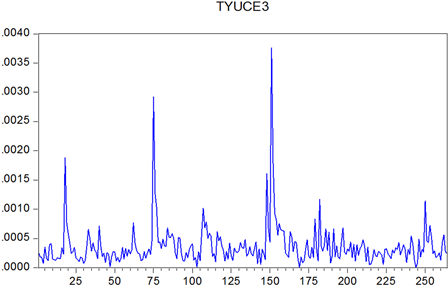
Figure 14. Improving T-GARCH’s forecast volatility of Shenzhen Stock
图14. 改进T-GARCH深证预测波动率
5. 总结
关于GARCH族模型的研究已经有几十年的历史,然而设法改进GARCH族模型来达到对股市更加精确的估计的研究仍在继续。本文在查阅大量文献的基础上,成功把成交金额这一新的影响股价波动的影响因子加入到GARCH族模型中,使得改进后的GARCH族模型可以直观地通过观察系数看出成交额这一影响因子对股市波动的贡献率。并且对上证指数和深证成指的实证分析表明,利用改进后的模型对股市波动率做出预测比原有模型预测的效果要好。通过对预测波动率图像和真实波动率图像的比较,已经能明显看出波动的趋势大致相同,但是局部图像仍有一些差别,说明模型仍有待进一步分析完善。
参考文献