关于混合Sine椭球的体积不等式

Volume Inequalities of the Mixed Sine Ellipsoid

摘要: 基于Sine椭球的定义和混合锥体积泛函，引入了一个新椭球。此外，本文进一步得到了新椭球的体积不等式，并得到了等式成立条件。

Abstract: Associated with the sine ellipsoid and the mixed cone-volume functional, a new ellipsoid is intro-duced in this paper. Moreover, volume inequality of this ellipsoid is established, and the equality condition is found in this paper.

1. 引言

众所周知，椭球是凸几何分析中一个重要的研究对象，经常出现在等周问题和一些极值问题里。例如，著名的John椭球是凸体包含的最大体积的椭球，被广泛的应用于凸几何分析和Banach空间几何。近些年来，椭球得到了广泛的关注并产生了大量的深刻结果 [1] [2] [3]。本文中所涉及的n-维欧式空间 $R^n$ 中的凸体和星体分别是包含原点在其内部的非空紧凸集和包含原点在其内部的非空紧星形集。用 ${\omega }_n$ 表示单位球B在 $R^n$ 中的体积。我们分别用 $K_o^n$ 和 $S_o^n$ 来表示 $S_{}^n$ 中的凸体和星体组成的集合。在经典力学中，与凸体K相关的惯量椭球 ${\Gamma }_{2}K$ 是指在任一方向上他们有相同的转动惯量，这个椭球就是熟知的Legendre椭球。对于 $K\in S_o^n$ 和 $u\in S^{n-1}$，它的支撑函数定义为：

$h_{{\Gamma }_{2}K}^2=\left(n+2\right){\displaystyle \underset{K}{\int }{\left|u\cdot x\right|}^2}\text{d}x/V\left(K\right)$ (1)

其中V(K)和 $x\cdot y$ 分别表示在 $R^n$ 中K的体积和x和y的标准内积。在文献 [4] 中，Lutwak，Yang和Zhang得到了如下体积不等式：

$V\left({\Gamma }_{2}K\right)\ge V\left(K\right)$ (2)

其中等号成立当且仅当K是关于原点中心对称的球。

勾股定理陈述为：如果 $x,y\in R^n$，则

${\left|x\cdot y\right|}^2+{\left[x,y\right]}^2={\left|x\right|}^2{\left|y\right|}^2$ (3)

其中 $\left|x\right|$ 表示x的n-维欧式范数， $\left[x,y\right]$ 表示由x和y张成的平行四边形的2维体积。受该定理的启发，Li，Huang和Xi在文献 [5] 中定义了Sine椭球：

$h_{{\Lambda }_{2}K}^2\left(x\right)=\left(n+2\right){\displaystyle \underset{K}{\int }{\left[x,y\right]}^2}\text{d}y/V\left(K\right)$ (4)

关于 ${\Lambda }_{2}K$ 的不等式(2)的模型被建立：对于 $K\in R^n$，则有

$V\left({\Lambda }_{2}K\right)\ge {\left(n-1\right)}^{n/2}V\left(K\right)$ (5)

其中等号成立当且仅当 $n\ge 3$ 时，K是关于原点中心对称的球。当 $n=2$ 时，K是关于原点中心对称的椭球。

作为Legendre椭球的对偶形式，Lutwak，Yang和Zhang [4] 引入了LYZ椭球，其径向函数定义为：

${\rho }_{{\Gamma }_{-2}K}^{-2}={\displaystyle \underset{S^{n-1}}{\int }{\left|u\cdot x\right|}^2}\text{d}{S}_2\left(K,v\right)/V\left(K\right)$ (6)

其中 $\text{d}{S}_2\left(K,v\right)$ 表示K的 $L_2$ 表面积测度。Hu和Xiong [6] 中定义了混合LYZ椭球，这启发我们定义两个新椭球 ${\Gamma }_2\left(K,L\right)$ 和 ${\Lambda }_2\left(K,L\right)$ ：对于 $K,L\in S_o^n$ 和 $x\in R^n$，则有

$h_{{\Gamma }_2\left(K,L\right)}^2=\left(n+2\right){\displaystyle \underset{K}{\int }{\left|x\cdot y\right|}^2}\text{d}y/V_1\left(K,L\right)$ (7)

$h_{{\Lambda }_2\left(K,L\right)}^2\left(x\right)=\left(n+2\right){\displaystyle \underset{K}{\int }{\left[x,y\right]}^2}\text{d}y/V_1\left(K,L\right)$ (8)

其中 $V_1\left(K,L\right)$ 表示K和L的第一混合体积。对于椭球 ${\Gamma }_2\left(K,L\right)$ 和 ${\Lambda }_2\left(K,L\right)$ 和它们极体有如下关系：

${\Gamma }_2\left(K,L\right){+}_2{\Lambda }_2\left(K,L\right)=c_{1}B,{\Gamma }_2^{*}\left(K,L\right){\widetilde{+}}_{-2}{\Lambda }_2^{*}\left(K,L\right)=B/c_1$

其中

$c_1^2=\left(n+2\right){\displaystyle \underset{K}{\int }{\left|y\right|}^2}\text{d}y/V_1\left(K,L\right).$

本文将得到有关椭球 ${\Lambda }_2\left(K,L\right)$ 的以下体积不等式。

定理1.1：如果 $K,L\in S_o^n$ 和L包含原点在其内部，那么

$V\left({\Lambda }_2\left(K,L\right)\right)\ge {\left(n-1\right)}^{n/2}V\left(K\right)$ (9)

其中等号成立当且仅当K和L是关于原点中心对称的球。

2. 预备知识

我们将列举有关凸体的一些背景知识，可以参考Schneider的有关凸体的百科全书 [7]。

如果 $K\in K_o^n$ 和 $y\in K$，那么K的极体定义为：

$K^{*}=\left\{x\in R^n,x\cdot y\le 1\right\}.$ (10)

它的支撑函数定义为：

$h_K=\max \left\{x\cdot y:y\in K\right\}$ (11)

对于 $\varphi \in GL\left(n\right)$，那么

$h_{\varphi K}\left(x\right)=h_K\left({\varphi }^{t}x\right).$ (12)

如果出 $c>0$，那么

$h_{cK}\left(x\right)=c{h}_K\left(x\right).$ (13)

如果 $K\in S_o^n$，其径向函数为：

${\rho }_K\left(x\right)=\max \left\{\lambda \ge 0:\lambda x\in K\right\}.$ (14)

通过(10)，(11)和(14)，有

$h_{K^{*}}={\rho }_K^{-1},{\rho }_{K^{*}}=h_K^{-1}$ (15)

对于 $\varphi \in GL\left(n\right)$，有

${\left(\varphi K\right)}^{*}={\varphi }^{-t}K.$ (16)

对于 $\epsilon >0$ 和 $K,L\in K_o^n$，那么K和L的Lp Minkowski-Firey 组合定义为：

$h_{K{+}_p\epsilon \cdot L}^p=h_K^p+h_L^p.$ (17)

关于 $K,L\in K_o^n$ 的Lp混合体积 $V_p\left(K,L\right)$ 定义为：

$V_p\left(K,L\right)=\frac{p}{n}\underset{\epsilon \to 0^{+}}{\lim }\frac{V\left(K{+}_p\epsilon \cdot L\right)-V\left(K\right)}{\epsilon },$

其积分表达式为：

$V_p\left(K,L\right)=\frac{1}{n}{\displaystyle \underset{S^{n-1}}{\int }{h}_L^p\left(v\right)\text{d}{S}_p\left(K,v\right)},$

其中

$\text{d}{S}_p\left(K,\cdot \right)=h_K{(\cdot )}^{1-p}\text{d}S\left(K,\cdot \right),$

是K的Lp表面积测度， $S\left(K,\cdot \right)$ 是K的经典表面积测度。特别地，

$V_p\left(K,K\right)=V\left(K\right).$

Lp Brunn-Minkowski不等式 [8] 陈述为：对于 $p\ge 0$ 和 $K,L\in K_o^n$，有

$V{\left(K{+}_{p}L\right)}^{p/n}\ge V{\left(K\right)}^{p/n}+V{\left(L\right)}^{p/n}$ (18)

其中等号成立当且仅当K和L是膨胀的。

对于 $\epsilon >0$ 和 $K,L\in S_o^n$，那么K和L的Lp 调和径向组合定义为：

${\rho }_{K{\widetilde{+}}_{-p}\epsilon \cdot L}^{-p}={\rho }_K^{-p}+{\rho }_L^{-p}.$ (19)

关于 $K,L\in S_o^n$ 的对偶Lp混合体积 $V_p\left(K,L\right)$ 定义为：

${\tilde{V}}_{-p}\left(K,L\right)=-\frac{p}{n}\underset{\epsilon \to 0^{+}}{\lim }\frac{V\left(K{\widetilde{+}}_{-p}\epsilon \cdot L\right)-V\left(K\right)}{\epsilon },$

其积分表达式为：

${\tilde{V}}_{-p}\left(K,L\right)=\frac{1}{n}{\displaystyle \underset{S^{n-1}}{\int }{\rho }_K^{n+p}\left(v\right){\rho }_L^{-p}\left(v\right)\text{d}v},$

这个积分是关于球面Lebesgue测度的积分。特别地，

${\tilde{V}}_{-p}\left(K,K\right)=V\left(K\right).$

对偶Lp Brunn-Minkowski 不等式陈述为：对于 $p>0$ 和 $K,L\in S_o^n$，有

$V{\left(K{\widetilde{+}}_{-p}L\right)}^{-p/n}\ge V{\left(K\right)}^{-p/n}+V{\left(L\right)}^{-p/n}$

其中等号成立当且仅当K和L是膨胀的。

椭球 ${\Gamma }_{2}K$ 和 ${\Gamma }_{-2}K$ 有如下体积不等式：对于 $K\in K_o^n$，有

$V\left({\Gamma }_{2}K\right)\ge V\left({\Gamma }_{-2}K\right)$ (20)

其中等号成立当且仅当K和L是关于原点中心对称的椭球。由混合Legendre椭球的定义，我们有

${\Gamma }_2\left(\varphi K,\varphi L\right)=\varphi {\Gamma }_2\left(K,L\right).$ (21)

假设A是正定的 $n\times n$ 对称矩阵，椭球 $E\left(A\right)=\left\{y\in R^n:y\cdot Ay\le 1\right\}$ 的支撑函数和径向函数为：

$h_{E\left(A\right)}^2\left(x\right)=x\cdot A^{-1}x,{\rho }_{E\left(A\right)}^{-2}\left(x\right)=x\cdot Ax.$ (22)

$\left[x,y,v_3,\cdots ,v_k\right]$ 表示 $x,y,v_3,\cdots ,v_k,k\ge 3$ 张成的超平行体的体积，有如下引理 [5]。

引理2.1：如果 $p>0$ 和 $\left[x,y\right]\ne 0$，那么

${\displaystyle \underset{S^{n-1}}{\int }\cdots }{\displaystyle \underset{S^{n-1}}{\int }{\left[x,y,v_3,\cdots ,v_n\right]}^p/{\left[x,y\right]}^p}\text{d}{v}_3\cdots \text{d}{v}_n,$ (23)

是一个仅仅与n和p有关的常数，特别地

${\displaystyle \underset{S^{n-1}}{\int }\cdots }{\displaystyle \underset{S^{n-1}}{\int }{\left[x,y,v_3,\cdots ,v_n\right]}^2/{\left[x,y\right]}^2}\text{d}{v}_3\cdots \text{d}{v}_n=\left(n-2\right)!{\omega }_n^{n-2}.$ (24)

文献 [7] 中的不等式(5.133)表述为：如果 $Q_1,\cdots ,Q_n$ 是正定的 $n\times n$ 矩阵，那么

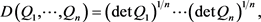(25)

其中等号成立当且仅当 $Q_i=Q_1,i=2,\cdots ,n$ 对于实数 ${\lambda }_i$ 成立。在 $S^{n-1}$ 上的Borel测度 $\mu$ 生成半正定的 $n\times n$ 矩阵 $\left[\mu \right]$ 定义为：

$\left[\mu \right]={\displaystyle \underset{S^{n-1}}{\int }\cdots }{\displaystyle \underset{S^{n-1}}{\int }v\otimes v}\text{d}\mu \left(v\right)$ (26)

其中 $v\otimes v$ 是在 $R^n$ 上的x到 $\left(x\cdot v\right)v$ 秩为1的线性算子。在文献 [8] 中证明了对于在 $S^{n-1}$ 上的Borel测度 ${\mu }_1,\cdots ,{\mu }_n$，判别式 $\left[{\mu }_1\right],\cdots ,\left[{\mu }_n\right]$ 定义为：

$D\left(\left[{\mu }_1\right],\cdots ,\left[{\mu }_n\right]\right)={\displaystyle \underset{S^{n-1}}{\int }\cdots }{\displaystyle \underset{S^{n-1}}{\int }{\left[v_1,\cdots ,v_n\right]}^2\text{d}{\mu }_1\left(v_1\right)\cdots \text{d}{\mu }_n\left(v_n\right)},$ (27)

结合(25)式，有

$D\left(\left[{\mu }_1\right],\cdots ,\left[{\mu }_n\right]\right)\ge {\left(\det \left[{\mu }_1\right]\right)}^{1/n}\cdots {\left(\det \left[{\mu }_n\right]\right)}^{1/n},$ (28)

其中等号成立当且仅当 $\left[{\mu }_i\right]={\lambda }_i\left[{\mu }_1\right],i=2,\cdots ,n$ 对于实数 ${\lambda }_i$ 成立。

3. 体积不等式

对于 $u\in S^{n-1}$，通过(17)，(1)，(8)，(7)，(3)和(13)，有

$h_{{\Gamma }_2\left(K,L\right){+}_2{\Lambda }_2\left(K,L\right)}^2\left(u\right)=h_{{\Gamma }_2\left(K,L\right)}^2\left(u\right)+h_{{\Lambda }_2\left(K,L\right)}^2\left(u\right)=\left(n+2\right){\displaystyle \underset{K}{\int }{\left|y\right|}^2\text{d}y}/V_1\left(K,L\right)=h_{c_{1}B}^2\left(u\right)=c_1^2.$

通过(19)，(15)和(16)，有

${\rho }_{{\Gamma }_2^{*}\left(K,L\right){\widetilde{+}}_{-2}{\Lambda }_2^{*}\left(K,L\right)}^{-2}\left(u\right)={\rho }_{{\Gamma }_2^{*}\left(K,L\right)}^{-2}\left(u\right)+{\rho }_{{\Lambda }_2^{*}\left(K,L\right)}^{-2}\left(u\right)=h_{{\Gamma }_2\left(K,L\right)}^2\left(u\right)+h_{{\Lambda }_2\left(K,L\right)}^2\left(u\right)=h_{c_{1}B}^2\left(u\right)={\rho }_{c_1^{-1}B}^{-2}\left(u\right),$

其中

$c_1^2=\left(n+2\right){\displaystyle \underset{K}{\int }{\left|y\right|}^2}\text{d}y/V_1\left(K,L\right).$

经典的Blaschke-Santalo不等式陈述为：对于 $K\in K_o^n$ 是原点对称的，那么

$V\left(K\right)V\left({\Gamma }_2^{*}K\right)\le {\omega }_n^2,$ (29)

其中等号成立当且仅当K是原点对称的椭球。Lutwak和Zhang在文献 [9] 中将(29)式推广到Lp空间。我们将建立椭球 ${\Lambda }_2^{*}\left(K,L\right)$ 形式的不等式(29)。

定理 3.1：如果 $K,L\in S_o^n$ 和L包含原点在其内部，那么

$V\left(K\right)V\left({\Lambda }_2^{*}\left(K,L\right)\right)\le {\omega }_n^2/{\left(n-1\right)}^{n/2},$ (30)

其中等号成立当且仅当K和L是原点对称的球。

假设 $K_2,\cdots ,K_n,L\in S_o^n$ 和L包含原点在其内部，对于 $p\ge 1$，凸体 $T_p\left(K_2,\cdots ,K_n,L\right)$ 的支撑函数定义为：

$h_{T_p\left(K_2,\cdots ,K_n,L\right)}^p\left(x\right)={\left(n+p\right)}^{n-1}{\displaystyle \underset{K_2}{\int }\cdots }{{\displaystyle \underset{K_n}{\int }\left[x,x_2,\cdots ,x_n\right]}}^p\text{d}{x}_2\cdots \text{d}{x}_n/V_1\left(K_2,L\right)V_1\left(K_3,B\right)\cdots V_1\left(K_n,B\right).$ (31)

通过极坐标转化为：

$h_{T_p\left(K_2,\cdots ,K_n,L\right)}^p\left(x\right)={\displaystyle \underset{S^{n-1}}{\int }\cdots }{{\displaystyle \underset{S^{n-1}}{\int }\left[x,v_2,\cdots v_n\right]}}^p{\rho }_{K_2}^{n+p}\left(v_2\right)\cdots {\rho }_{K_n}^{n+p}\left(v_n\right)\text{d}{v}_2\cdots \text{d}{v}_n/V_1\left(K_2,L\right)V_1\left(K_3,B\right)\cdots V_1\left(K_n,B\right).$ (32)

易知：凸体 $T_p\left(K_2,\cdots ,K_n,L\right)$ 是一个椭球。 $T_p$ 的仿射性如下：

定理3.2：如果 $p\ge 1$， $\varphi \in GL\left(n\right)$ 和 $K_2,\cdots ,K_n,L\in S_o^n$，那么

$T_p\left(\varphi K_2,\cdots ,\varphi K_n,\varphi L\right)={\left|\det \varphi \right|}^{\left(p+1\right)/p}{\varphi }^{-t}{T}_p\left(K_2,\cdots ,K_n,\varphi L\right).$

证明：通过(31)，(12)和(13)，有

$\begin{array}{l}{h}_{T_p\left(\varphi K_2,\cdots ,\varphi K_n,\varphi L\right)}^p\left(x\right)\\ ={\left(n+p\right)}^{n-1}{\displaystyle \underset{\varphi K_2}{\int }\cdots }{{\displaystyle \underset{\varphi K_n}{\int }\left[x,x_2,\cdots ,\varphi x_n\right]}}^p\text{d}{x}_2\cdots \text{d}{x}_n/V_1\left(\varphi K_2,\varphi L\right)V_1\left(\varphi K_3,B\right)\cdots V_1\left(\varphi K_n,B\right)\\ ={\left(n+p\right)}^{n-1}{\displaystyle \underset{K_2}{\int }\cdots }{{\displaystyle \underset{K_n}{\int }\left[x,\varphi x_2,\cdots ,\varphi x_n\right]}}^p{\left|\det \varphi \right|}^{n-1}\text{d}{x}_2\cdots \text{d}{x}_n/{\left|\det \varphi \right|}^{n-2}{V}_1\left(K_2,L\right)V_1\left(K_3,{\varphi }^{-1}B\right)\cdots V_1\left(K_n,{\varphi }^{-1}B\right)\\ ={\left(n+p\right)}^{n-1}{\displaystyle \underset{K_2}{\int }\cdots }{{\displaystyle \underset{K_n}{\int }\left[{\varphi }^{-1}x,x_2,\cdots ,x_n\right]}}^p{\left|\det \varphi \right|}^{p+1}\text{d}{x}_2\cdots \text{d}{x}_n/V_1\left(K_2,L\right)V_1\left(K_3,B\right)\cdots V_1\left(K_n,B\right)\\ ={\left|\det \varphi \right|}^{p+1}{h}_{T_p\left(K_2,\cdots ,K_n,L\right)}^p\left({\varphi }^{-1}x\right)=h_{{\left|\det \varphi \right|}^{\left(p+1\right)/p}{\varphi }^{-t}{T}_p\left(K_2,\cdots ,K_n,L\right)}^p\left({\varphi }^{-1}x\right).\end{array}$

对于 $p\ge 1$， $K,L\in S_o^n$ 和L包含原点在其内部，凸体 ${\Lambda }_p\left(K,L\right)$ 的支撑函数为：

$h_{{\Lambda }_p\left(K,L\right)}^p\left(x\right)=\left(n+p\right){\displaystyle \underset{K}{\int }{\left[x,y\right]}^p}\text{d}y/V_1\left(K,L\right).$

当 $p=2$ 时，凸体 ${\Lambda }_p\left(K,L\right)$ 是(8)中定义的椭球。

定理3.3：如果 $p\ge 1$， $K,L\in S_o^n$ 和L包含原点在其内部，那么仅仅存在一个与n，p有关的常数 $c_{n,p}>0$，使得

$T_p\left(K,B,\cdots ,B,L\right)=c_{n,p}{\Lambda }_p\left(K,L\right).$

特别地，

$T_2\left(K,B,\cdots ,B,L\right)={\left(\left(n-2\right)!\right)}^{1/2}{\Lambda }_2\left(K,L\right).$ (33)

证明：假设 $K_2=K$ 和把 $K_3=\cdots =K_n=B$ 代入(32)中，结合引理2.1，有

$\begin{array}{c}{h}_{T_p\left(K,B,\cdots ,B,L\right)}^p\left(x\right)={\displaystyle \underset{S^{n-1}}{\int }\cdots }{{\displaystyle \underset{S^{n-1}}{\int }\left[x,v_2,\cdots ,v_n\right]}}^p{\rho }_K^{n+p}\left(v_2\right)\text{d}{v}_2\cdots \text{d}{v}_n/V_1\left(K,L\right){\omega }_n^{n-2}\\ =c_{n,p}{{\displaystyle \underset{S^{n-1}}{\int }\left[x,v_2\right]}}^p{\rho }_K^{n+p}\left(v_2\right)\text{d}{v}_2/V_1\left(K,L\right)\\ =c_{n,p}\left(n+p\right){{\displaystyle \underset{K}{\int }\left[x,y\right]}}^p\text{d}y/V_1\left(K,L\right)\\ =h_{c_{n,p}{\Lambda }_p\left(K,L\right)}^p(x)\end{array}$

其中常数

$c_{n,p}={\left({\displaystyle \underset{S^{n-1}}{\int }\cdots }{{\displaystyle \underset{S^{n-1}}{\int }\left(\left[x,v_2,\cdots ,v_n\right]/\left[x,v_2\right]\right)}}^p\text{d}{v}_3\cdots \text{d}{v}_n/{\omega }_n^{n-2}\right)}^{1/p}.$

特别地 $c_{n,2}={\left(\left(n-1\right)!\right)}^{1/2}$，通过(24)，得到(33)。

定理3.4：如果 $K_2,\cdots ,K_n,L\in S_o^n$ 和L包含原点在其内部，那么

$V\left({\Gamma }_2\left(K_2,L\right)\right)\cdots V\left({\Gamma }_2\left(K_n,L\right)\right)V\left(T_2^{*}\left(K_2,\cdots ,K_n,L\right)\right)\le {\left(\left(n-1\right)!\right)}^{-n/2}{\omega }_n^n,$ (34)

其中等号成立当且仅当 ${\Gamma }_2\left(K_i,L\right),i=2,\cdots ,n$ 是球。

证明：通过(21)，(16)，不等式(34)的左边是 $GL\left(n\right)$ 不变量，那么我们假设

$T_2\left(K_2,\cdots ,K_n,L\right)=B,$ (35)

则有

$1=h_{T_2\left(K_2,\cdots ,K_n,L\right)}^p\left(v\right)={\displaystyle \underset{K_2}{\int }\cdots }{{\displaystyle \underset{K_n}{\int }\left[x,v_2,\cdots ,v_n\right]}}^2{\rho }_{K_2}^{n+2}\cdots {\rho }_{K_n}^{n+2}\text{d}v\text{d}{v}_2\cdots \text{d}{v}_n/V_1\left(K_2,L\right)V_1\left(K_3,B\right)\cdots V_1\left(K_n,B\right).$ (36)

关于球面Legendre测度积分得

$n{\omega }_n={\displaystyle \underset{K_2}{\int }\cdots }{{\displaystyle \underset{K_n}{\int }\left[x,v_2,\cdots ,v_n\right]}}^2{\rho }_{K_2}^{n+2}\cdots {\rho }_{K_n}^{n+2}\text{d}v\text{d}{v}_2\cdots \text{d}{v}_n/V_1\left(K_2,L\right)V_1\left(K_3,B\right)\cdots V_1\left(K_n,B\right).$ (37)

通过(26)和(27)，有

$D\left(\left[B\right],\left[K_2,L\right],\cdots ,\left[K_n,L\right]\right)=1/\left(n-1\right)!,$ (38)

其中 $D\left(\left[B\right],\left[K_2,L\right],\cdots ,\left[K_n,L\right]\right)$ 关于正定的 $n\times n$ 矩阵的判别式定义为

$\left[B\right]={\displaystyle \underset{S^{n-1}}{\int }v\otimes v\text{d}v}/{\omega }_n=I_n,$ (39)

$\left[K_2,L\right]=\left(n+2\right){\displaystyle \underset{K_2}{\int }y\otimes y\text{d}y}/V_1\left(K_2,L\right),$ (40)

$\left[K_i,L\right]=\left(n+2\right){\displaystyle \underset{K_i}{\int }y\otimes y\text{d}y}/V_1\left(K_i,B\right),$ (41)

通过(1)，(22)，(38)，(39)，(28)和(35)，得

$\begin{array}{l}1/\left(n-1\right)!=D\left(\left[I_n\right],\left[K_2,L\right],\cdots ,\left[K_n,L\right]\right)\\ \ge {\left(V\left({\Gamma }_2\left(K_2,L\right)\right){\omega }_n^{-1}\right)}^{2/n}\cdots {\left(V\left({\Gamma }_2\left(K_n,L\right)\right){\omega }_n^{-1}\right)}^{2/n}\\ =V{\left({\Gamma }_2\left(K_2,L\right)\right)}^{2/n}\cdots V{\left({\Gamma }_2\left(K_n,L\right)\right)}^{2/n}V{\left(T_2^{*}\left(K_2,\cdots ,K_n,L\right)\right)}^{2/n},\end{array}$

得到不等式(34)。通过(28)，(39)中的等式成立当且仅当 $\left[K_i,L\right]={\lambda }_i{I}_n,i=2,\cdots ,n$ 对于实数 ${\lambda }_i$。进而得到 ${\Gamma }_2\left(K_i,L\right),i=2,\cdots ,n$ 是球。

定理3.5：如果 $K_2,\cdots ,K_n,L\in S_o^n$ 和 $K_2,\cdots ,K_n\subseteq L$，那么

$V\left(K_2\right)\cdots V\left(K_n\right)V\left(T_2^{*}\left(K_2,\cdots ,K_n,L\right)\right)\le {\left(\left(n-1\right)!\right)}^{-n/2}{\omega }_n^n,$ (42)

其中等号成立当且仅当 $K_i,L,i=1,\cdots ,n$ 是关于原点中心对称的球。

证明：通过(2)和(34)，我们有

$\begin{array}{l}{\left(\left(n-1\right)!\right)}^{-n/2}{\omega }_n^n\ge V\left({\Gamma }_2\left(K_2,L\right)\right)\cdots V\left({\Gamma }_2\left(K_n,L\right)\right)V\left(T_2^{*}\left(K_2,\cdots ,K_n,L\right)\right)\\ \ge V\left({\Gamma }_2{K}_2\right)\cdots V\left({\Gamma }_2{K}_n\right)V\left(T_2^{*}\left(K_2,\cdots ,K_n,L\right)\right)\\ \ge V\left(K_2\right)\cdots V\left(K_n\right)V\left(T_2^{*}\left(K_2,\cdots ,K_n,L\right)\right),\end{array}$

由(34)的等式条件和(2)，不等式(42)等式成立当且仅当 $K_i,L,i=1,\cdots ,n$ 是关于原点中心对称的球。

通过定理3.4和(16)，得到定理3.1。结合不等式(29)和 ${\Lambda }_2\left(K_i,L\right)$ 是关于原点中心对称的球得到不等式(9)。