1. 引言
全球气候变暖正在引起越来越多的关注,温室气体增加和环境污染等问题都推动着新能源技术的发展,风力发电已经成为目前新能源应用中最成熟的技术之一 [1] [2]。目前,中国大规模开发利用的风能主要集中在风能资源丰富的“三北”地区和东南沿海,这些地区风资源好,平均风速较高,其装机容量占我国风电总装机容量的绝大部分。但是,目前高风速地区装机逐渐达到饱和以及电网消纳能力有限,弃风限电现象日益严重。实际上,我国低风速风能资源也非常丰富,在此背景下,国家风电发展规划明确表示要加快开发中东部和南方地区陆上风能资源,低风速风电也符合我国经济和风能资源分布的开发战略。因此,针对我国风电利用和经济发展国情而言,低风速风电的相关研究十分重要 [3]。风力机叶片是风力机系统中最为重要的部件之一,其直接关系到机组的风能利用效率和气动载荷 [4]。鉴于目前国内低风速风资源现状,翼型的设计在低风速风力机研究中举足轻重,决定了风能利用的经济性 [5]。目前国内外已经有很多学者开展了风力机翼型相关的研究。Kenneth W. Van Treuren等学者对比研究了多种不同翼型在低风速环境下的性能,发现最低噪声水平对应的攻角和最大升阻比对应的攻角非常接近。而且,相比较E387,S823,NACA0012和NACA4412这几种翼型,NACA4412在气动噪声和升阻特性等方面都具有明显优势 [6]。代元军等学者通过对S型翼型绕流流场进行数值模拟,并对比其实测数据,最后证实了S翼型具有气动性能良好的优点 [7] [8]。N. Karthikeyan等学者对不同厚度的翼型进行了对比研究,发现薄翼型相对而言具有更高的升力特性,而且在噪声方面也更有优势 [9]。Muhammad S. Virk的研究也指出,厚翼型比薄翼型更容易发生流动分离现象 [10]。因此,本文结合现有文献,选择目前比较有代表性的NACA4412、S8037和S1091这三种翼型作为对象,分别针对这三种翼型进行流动和气动特性研究,并比较其在低风速环境下的性能表现,旨在为低风速风力机设计和优化提供参考和借鉴。
2. 控制方程和数值模型
2.1. 控制方程
对于低风速风力机绕流,流场中的密度变化很小,因此,可以假设其绕流流动为不可压缩流动 [11]。此外,流场中温度的变化不大,粘性系数随温度的变化可以忽略。边界层流体分离和流体的粘性有关,因此在计算时不能忽略流体的粘性。基于稳态不可压缩流动,对纳维–斯托克斯方程(Navier-Stokes方程)进行数值求解,得到直角坐标系下N-S方程的流体控制方程张量的形式表达:
(1)
连续性方程:
(2)
式中: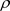 是流体的密度;
是流体的密度; 是流体的速度;fi是质量力 [12]。
是流体的速度;fi是质量力 [12]。
2.2. 湍流模型
本文采用对边界层湍流和自由剪切湍流均有良好模拟效果的SST模型。该模型结合了k-ω模型和k-ε模型的优点,是一种两方程湍流模型 [13]。通过混合函数从边界层内部到外部完成从适用于低雷诺数的k-ω模型到适用于高雷诺数的k-ε模型的逐渐转变,其输运变量为湍动能k和比耗散率ω,运输方程为:
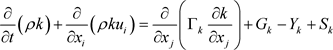 (3)
(3)
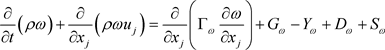 (4)
(4)
其中 为湍动能,
为湍动能,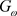 由
由 得出,
得出, 和
和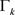 分别表示
分别表示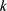 和
和 的耗散项,
的耗散项, 表示交叉扩散项,
表示交叉扩散项, 和
和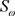 为原项 [14]。
为原项 [14]。
2.3. 翼型建模及网格划分
2.3.1. 三种风力机翼型
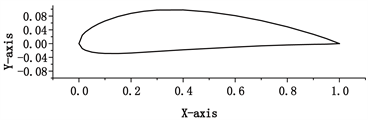
NACA翼型族是美国最早建立的一个低速翼型系列,有较高的最大升力系数和较低的阻力系数。S翼型族具有最大升力系数对粗糙度不敏感,以及失速特性良好的特性 [15]。本文主要针对NACA4412,S8037以及S1091三种翼型进行研究,分析其在低风速下的性能表现。图1为本文进行对比研究的三种翼型二维模型图。NACA4412翼型如图1(a)所示,该翼型最大弯度为4%,在弦长的40%位置;最大厚度为12%,在弦长的30%位置。S8037翼型如图1(b)所示,该翼型是一种低雷诺数翼型,最大弯度为1.9%,在弦长的40.4%位置;最大厚度为16%,在弦长的33.5%位置。S1091翼型如图1(c)所示,该翼型最大弯度为5.7%,在弦长的45%位置;最大厚度为5.1%,在弦长的13.4%位置。
2.3.2. 翼型建模及网格划分
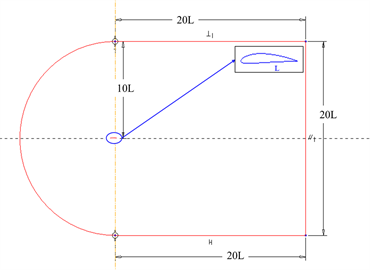
本文针对三种不同的翼型,传统翼型NACA4412,S翼型S8037、薄翼型S1091进行二维建模分析。获取这三种翼型的二维点集数据后,通过矩阵进行坐标转换,并将点集导入ANSYS进行建模和网格划分。NACA4412翼型的计算域如图2(a)所示,计算域网格划分及翼型尾缘网格局部放大如图2(b)所示。翼型的弦长L = 1000 mm,半圆形来流入口半径为10 L,出口距离翼型中心和20 L处;以避免壁面边界对流场产生影响,并使得流动能够充分发展 [16]。入口边界条件为速度入口为5 m/s;出口边界条件为压力出口;翼型表面设为无滑移壁面边界;各项残差精度设为 。空气为不可压缩,忽略重力影响;流动设为定常流动;流场中只存在单项流动,且不考虑风沙等多相流的情况。
。空气为不可压缩,忽略重力影响;流动设为定常流动;流场中只存在单项流动,且不考虑风沙等多相流的情况。
 (a)
(a) 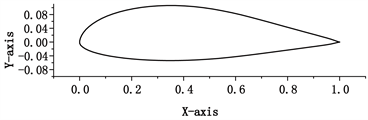 (b)
(b)  (c)
(c)
Figure 1. Profiles of three kinds of airfoils. (a) NACA4412 airfoil profile; (b) S8037 airfoil profile; (c) S1091 airfoil profile
图1. 三种风力机翼型二维模型。(a) NACA4412翼型;(b) S8037翼型;(c) S1091翼型
 (a)
(a)  (b)
(b)
Figure 2. CFD domain. (a) 2-D model domain; (b) mesh computational domain
图2. CFD计算模型。(a) 二维模型;(b) 计算域网格
本文利用FLUENT 17.0的分离求解器,设置压力速度耦合求解,采用压力耦合方程组的半隐式(SIMPLEC)算法;动量方程及湍流粘性系数均采用二阶精度迎风格式求解。在结构化网格基础上进行计算,网格数量与升力系数的关系如图3所示。本文通过调整网格尺寸的大小进行计算,以确定计算结果满足精度要求时的网格数的范围。当网格数量小于14万时,翼型升阻比一直处于上升趋势,偏差波动较大;当网格数量大于14万时,升力系数监测值趋于稳定,偏差降低至0,表明此时网格质量和网格数达到计算要求。因此,本文后续研究的模型网格数量均为14万左右。
基于本文的网格划分方法和边界条件设置,对比Qblade中NACA4412翼型数据与计算结果在风速为5 m/s、攻角为0˚工况下的压力系数。本文模型计算结果和Qblade数据对比如图4所示,两者压力系数曲线较为吻合,对比结果表明了本文的数值模型的有效性 [17]。
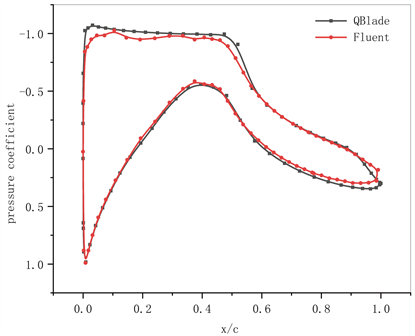
Figure 4. Pressure coefficient comparison of airfoil NACA4412
图4. NACA4412翼型压力系数对比
3. 三种风力机叶片翼型的流动特性分析
三种风力机叶片翼型的速度云图和流线图如图5至图7所示。在尚未失速条件下,随着攻角的增大,翼型上表面的流速均呈增加趋势。根据翼型数据,S8037翼型在前缘处上表面型线斜率为3.07,而NACA4412和S1091相同位置的斜率分别为1.95和1.70 [18] [19] [20]。因此S8037翼型前缘处斜率相对另外两种翼型稍大一些,来流在该翼型表面的增速效果也要优于另外两种翼型。根据伯努利原理,流速大的区域形成负压区,流速小的区域形成正压区,S8037上表面产生更大的负压区;而S8037翼型下表面的型线设计导致来流发生较小的增速,因此减小了S8037翼型的上下表面压差,削弱了其气动特性。对比发现S1091翼型下表面的型线斜率特性和S8037相反,具有阻流效果,使得翼型下表面来流速度减小,产生更大的正压区。
 (a)
(a)  (b)
(b)  (c)
(c) 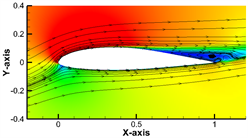
Figure 5. Velocity distribution and streamlines of airfoil NACA4412. (a) Angle of attack = 3˚; (b) Angle of attack = 6˚; (c) Angle of attack = 12˚
图5. 翼型NACA4412速度云图和流线图。(a) 攻角3˚;(b) 攻角6˚;(c) 攻角12˚
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 6. Velocity distribution and streamlines of airfoil S8037. (a) Angle of attack = 3˚; (b) Angle of attack = 6˚; (c) Angle of attack = 12˚
图6. 翼型S8037速度云图和流线图。(a) 攻角3˚;(b) 攻角6˚;(c) 攻角12˚
 (a)
(a)  (b)
(b)  (c)
(c)
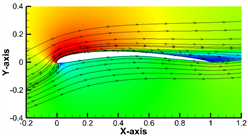
Figure 7. Velocity distribution and streamlines of airfoil S1091. (a) Angle of attack = 3˚; (b) Angle of attack = 6˚; (c) Angle of attack = 12˚
图7. 翼型S1091速度云图和流线图。(a) 攻角3˚;(b) 攻角6˚;(c) 攻角12˚
分析速度云图,在上表面负压区和下表面正压区的前缘交界处,存在一个流速和压力都为零的位置,即驻点。以此为分界形成上下表面的流速和压力差,从而为翼型提供升力。从速度云图可知压力在翼型表面上的分布特性:最大负压区和最大正压区集中在翼型前缘位置,该现象在大攻角下更为明显,如图5至图7所示。吸力面上最低压强点非常接近前缘,该表面的来流几乎90%在逆压力梯度区域内,会导致边界层内的流动很快变为湍流,因而翼型表面的湍流摩擦阻力占比很大,导致翼型的阻力系数较大。在小攻角下,三种翼型的流线始终沿着翼型表面,没有发生较为明显的气流分离;对比图5(c),图6(c)中翼型在大攻角下的流线图,气流在翼型的尾缘位置脱落,发生涡流,而如图7(c)所示,S1091翼型的流动分离程度相对较弱。
4. 升阻特性分析
为了研究低风速工况,攻角变化对翼型气动性能的影响规律及其性能差异,本文选取4 m/s,5 m/s,6 m/s的低风速工况,对这三种翼型在不同攻角下的升阻特性进行数值仿真,并对比分析其升阻比曲线。
模拟数据如图8所示,翼型的升阻比随着攻角的增大呈先增大后减小的趋势。在小攻角工况下,气流流经翼型表面在翼型尾部还没有发生分离,由于随着攻角的增大升力增大比较明显,而阻力变化不大,因此升阻比呈上升趋势;在大攻角工况下,气流在翼型尾部发生分离脱落现象愈加明显,阻力变化依然很小,但是升力下降明显,因此升阻比呈下降趋势。
 (a)
(a) 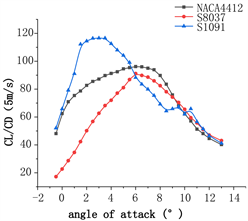 (b)
(b) 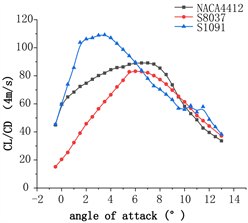 (c)
(c)
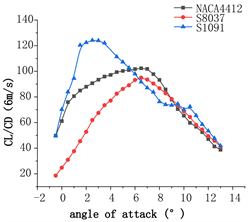
Figure 8. Comparison of lift-drag ratio at different wind speeds. (a) Lift-drag ratio at 4 m/s; (b) Lift-drag ratio at 5 m/s; (c) Lift-drag ratio at 6 m/s
图8. 不同风速翼型升阻比对比。(a) 风速4 m/s升阻比曲线;(b) 风速5 m/s升阻比曲线;(c) 风速6 m/s升阻比曲线
计算结果表明,在4~6 m/s的低风速范围,这三种翼型最大升阻比对应的攻角变化不大,这说明在低风速区间,翼型最佳攻角比较稳定。在低风速4~6 m/s范围,NACA4412和S8037最佳攻角为6˚,S1091最佳攻角为3˚。分析这三种翼型的最佳升阻比,NACA4412翼型的 为96.17,S8037翼型的
为96.17,S8037翼型的 为91.15,S1091翼型升阻比最大,
为91.15,S1091翼型升阻比最大, 为116.60。对比发现S1091翼型升阻特性最优,相较于另外两种翼型,其升阻特性高出30%左右。
为116.60。对比发现S1091翼型升阻特性最优,相较于另外两种翼型,其升阻特性高出30%左右。
通过对比分析在不同攻角下三种翼型的流动和升阻特性发现,在低风速工况下S1091翼型在最佳攻角位置能够获得更优的升阻比,而且其较高的升阻比覆盖更低攻角范围,在小攻角范围气流更不容易发生脱落和分离。因此,S1091翼型具有较好的升阻特性,更适用于低风速工况。
5. 结论
本文对比分析了NACA4412,S8037和S1091三种翼型在低风速条件下的气动特性,并通过对比分析其性能特点和规律,旨在为低风速风力机设计和优化提供指导,主要结论如下:
1) 随着攻角的逐渐增大,来流逐渐在三种翼型尾缘发生流动分离,形成涡流,降低翼型的升阻特性;对比三种翼型,S1091翼型在大攻角下的流动分离程度小于NACA4412翼型和S8037翼型。
2) 对于本文研究的NACA4412、S8037及S1091三种翼型,在低风速条件下,三种翼型在不同攻角下的升阻比变化规律不受风速变化的影响。
3) 在低风速条件下,NACA4412、S8037及S1091三种翼型分别在攻角为6˚、6˚和3˚时达到最大升阻比,且S1091翼型的最大升阻比相较于另外两种翼型最大升阻比高出30%左右,更适用于低风速工况。
基金项目
国家自然科学基金(51976067);湖北省技术创新专项重大项目(编号:2017AAA035);低品位能源利用技术及系统教育部重点实验室开放基金(No. LLEUTS-201905)。
NOTES
*通讯作者。