1. 引言
重积分是微积分学中的一个重要内容,在实际中有着非常重要的应用,因此重积分的计算至关重要。由于重积分在计算时,可能会有多种解法,而有的重积分在用一般的解题方法时很困难,因此需要通过重积分的变量变换来解决积分计算中所遇到的问题,利用简单而又方便的变量变换的方法来解决复杂的重积分计算问题,能为重积分的应用带来更多的便利。
变量变换方法的重点就在于分析被积函数和积分区域的特点,选择合适的变换方法,从而达到可以简便计算的目的,重积分常见的坐标变换有二重积分的极坐标变换,三重积分的柱坐标变换和球坐标变换。本文将在已有变换方法的基础上探寻不同的变量变换方法,使得积分计算具有简便性。
2. 重积分的变量变换
2.1. n重积分的变量变换公式
在有界闭区域V上是可积函数,设变换
将n维
空间中的区域
一一对应地映在
空间上,并形成区域V,函数
分别有连续的一阶偏导数且它函数行列式
则
上式为一般的n重积分的变量变换公式 [1],实际中常常遇到的是
时二重积分以及
时三重积分的计算与应用,文献 [2] [3] [4] [5] [6] 对常见的换元积分法做了讨论及推广,下面着重探讨两种特殊区域的二重积分和三重积分的变量变换公式。
2.2. 积分区域由两族曲线围成的二重积分变量变换公式
如果积分区域D由两族光滑的曲线
中分别取了两条曲线
。
所围成,且 在D上连续,作变量变换
,则
在D上连续,作变量变换
,则
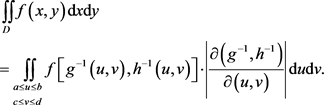
其中
为
的反函数组,
。
2.3. 积分区域由三族曲面围成时的三重积分变量变换公式
如果空间区域V由三族光滑的曲面中分别取了两条曲面
,
,
;
,
,
;
,
,
所围成,且
在V上连续,作变量变换
则
其中
为
的反函数组,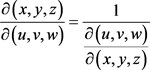 。
。
3. 变量变换在重积分计算问题中的应用
例1:计算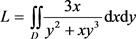 ,其中D为平面曲线
所围成的有界闭区域。(武汉大学)
,其中D为平面曲线
所围成的有界闭区域。(武汉大学)
分析:作积分区域D,如下:
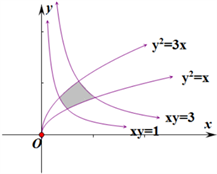
积分区域的边界线方程为
,
,作变换
,使得积分限容易确定。
解:作变换
,则积分区域D变为
例2:计算下面曲面所围成的图形的体积:
,
。(吉林工业大学)
分析:求体积即求被积函数为1的三重积分,积分区域由三族光滑的曲面
,
,
,分别取了两个曲面,也就是当 a = 1,2,b = ±1,c = ±1 时,所以可以利用曲面函数作相应的变换。
解:作变换,
则积分区域V变为
则
4. 结语
本文通过常用的重积分的变量变换公式给出了一种由几族曲线(面)围成的积分区域的变量变换方法,并利用该变量变换方法解决了实际的重积分计算问题。
基金项目
陕西省教育科学规划课题(SGH17H243)。