1. 引言
由于在工业和军事中的重要应用,多智能体控制系统在过去十年中被广泛研究。多智能体系统的研究内容主要包含一致性协作控制问题 [1]、编队控制问题 [2]、蜂拥问题、聚集问题等,其中一致性协作控制是最基本的研究问题。多智能体系统的一致性问题,就是设计智能体局部之间的作用方式,通过各智能体利用邻居传来的信息,不断调整自己的行为,使所有的智能体的状态(如位置、速度、加速度等)随着时间的推移达到共同的值。当前多智能体系统协作一致性已广泛应用于无线传感器网络 [3]、无人机编队控制 [4] [5]、可移动机器人的编队控制 [6] 等。在海洋勘探、野外搜索探测、协同作战等领域,多智能体系统有着广阔的应用前景。
在多智能体系统的实际应用中,如何减少多智能体间的通信频次以减少对网络带宽、通信成本及智能体自身能量等有限资源的不必要浪费是当前的一个重要研究课题。近些年来,基于事件触发机制的多智能体系统一致性问题受到大量学者的关注 [7] - [12]。由于周期事件触发控制可以有效地排除Zeno行为,该种控制方式被引入到多智能体系统的一致性研究中 [13]。Meng等 [14] 基于无向图研究了一阶多智能体系统在固定和切换拓扑下的周期事件触发平均一致性问题。Fan等 [15] 基于周期事件触发的方法研究了一阶多智能体系统一致性问题。由于现实系统的复杂性,许多情形下,时滞问题成为一个必须要研究的问题。Wang等 [16] 采用事件触发控制的方法研究了存在常通信时滞的多智能体系统的平均一致性问题。Liu等 [17] 采用周期采样和事件混合控制方法,研究了带有通信时滞的一阶多智能体系统在无向拓扑和有向拓扑下的一致性问题,基于采样和事件触发混合测量状态,可以显著减少控制器的更新次数。Xie等 [18] 基于有向网络对具有通信时滞的一阶多智能体系统的一致性问题进行了研究。在 [19] 中,Wang等对具有时变通信时滞的多智能体系统的事件触发一致协议进行了设计和研究,通过对事件触发条件的设计,使得所有跟随者能够以较低的通信频率跟踪领导者的状态。
基于以上研究,本文对一阶多智能体系统平均一致性问题进行了进一步研究。本文研究了具有时变时滞的多智能体平均一致性问题,通过利用 [20] 得出的有向图相关结论,在混合式事件触发条件下,通过构造李雅普诺夫函数,利用稳定性理论,分析给出了多智能体系统实现状态一致的条件。
本文共分为三部分,首先给出了代数图论相关知识并设计出具有时变时滞的多智能体系统一致性协议。然后基于有向图对多智能体系统加以分析和研究,通过构造李雅普诺夫函数将多智能体系统的一致性问题转换成一个相应系统的稳定性问题。进一步,利用稳定性定理分析给出多智能体系统达到平均一致性的条件。最后,利用仿真实例说明了所得结论的有效性。
2. 问题陈述
2.1. 图论知识
在多智能体系统的协作控制中,通常假定每个智能体可以通过彼此间的通信来获取其它智能体的状态信息,智能体间的通信网络用有向图或无向图来表示。
在有向图中,具有权重的有向通信网络通常用
表示,其中
代表顶点集,
用来表示智能体i,E代表边集,边集E由 组成,表示智能体j到智能体i有信息通讯,其中
且
。如果称
为
的邻居,当且仅当存在一条从
指向
的边。
邻居的集合用
来表示,即
。邻接矩阵
定义为:若
,那么
,否则
。
称为图
的拉普拉斯矩阵,其中
。如果
,则称图G是平衡的。对于顶点
和
,若存在一个顶点序列
,其中
组成,表示智能体j到智能体i有信息通讯,其中
且
。如果称
为
的邻居,当且仅当存在一条从
指向
的边。
邻居的集合用
来表示,即
。邻接矩阵
定义为:若
,那么
,否则
。
称为图
的拉普拉斯矩阵,其中
。如果
,则称图G是平衡的。对于顶点
和
,若存在一个顶点序列
,其中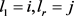 ,
为
的邻居,k = 1,2,…, r −1 ,则称
,
为
的邻居,k = 1,2,…, r −1 ,则称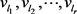 组成一条有向路径。如果对于每一对
和
,
,从
到
和
到
都存在有向路径使之连接,则称有向图是强连通的。
组成一条有向路径。如果对于每一对
和
,
,从
到
和
到
都存在有向路径使之连接,则称有向图是强连通的。
在无向图中,如果两个顶点通过边相连,则称这两个点是相邻的。称图是连通的,当且仅当任意两个不同的顶点之间存在一条路径。用无向图
表示有向图G的镜像,其定义为:无向图
与有向图G具有相同的节点,图
的边由G中的有向边与每条边的反向边共同组成。
的邻接矩阵用
表示,其中
,
。
的拉普拉斯矩阵记为
。
2.2. 模型建立
考虑具有n个智能体的多智能体系统,其动态方程表述如下:
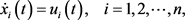 (1)
(1)
其中
表示智能体i的状态,
表示控制输入,控制协议根据智能体自身状态和从邻居处接收到的局部信息设计。
在本文中,我们采用周期事件检验的方法来验证事件触发条件并决定智能体应该何时更新控制输入。假设
为事件检验时刻,其中h是固定的正数,为事件检验周期。所有智能体在信息传递过程中存在时滞
,满足
,
。为表达方便,定义
,
,
。又记
,其中
表示智能体i的事件触发时刻序列,
。系统(1)的控制输入设计为
(2)
结合(1)和(2),有
(3)
其中
,
。
对于每个智能体i,定义测量误差为当前状态与最近事件触发时刻状态的差值,即
。对于任意
,智能体i的下一触发时刻由如下事件触发条件确定:
(4)
其中
是正数,
。如果
满足事件触发条件,则
,即
。
如果智能体i的事件触发条件在某个事件检验时刻被满足,则智能体i对其状态进行采样,并将采样信息传递给其邻居。因为时滞
,
比事件检验周期小,在下一次事件检验时刻前,智能体
的所有邻居都会得到其采样的状态信息。
3. 主要结果
这一部分我们研究在不同事件触发条件下的具有时变时滞多智能体系统的平均一致性问题,并得出相应结论。
引理1. [17] 假设有向图是强连通平衡的,
为其对应的拉普拉斯矩阵,对任意的
,有如下等式成立,
其中
是
的最大特征值,
是
的最小正特征值。
定理1. 假设有向图是强连通平衡的。对所有的
,如果存在
,使得如下条件满足,
(5)
则所有智能体将实现平均一致。
证明:考虑Lyapunov函数
对(3)进行积分得到
(6)
当
,对
进行求导,结合(6)可以得到
 (7)
(7)
由引理1,可以进一步得到如下不等式
(8)
由于
(9)
所以由(7),(8),(9)可以得到
由于
可以得到
因为有向图是平衡的,可以得到
(10)
由事件触发条件(4)可知
(11)
由(10)和(11)可以进一步得到
(12)
由条件(5)得

因为
由
非负,所以可以得到
。注意到 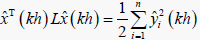 ,所以
。由(11)可以进一步得到
。由于
,由引理1可得
。所以
,进而由引理1和(6)得到
,所以
。由(11)可以进一步得到
。由于
,由引理1可得
。所以
,进而由引理1和(6)得到  ,因此所有智能体状态达到平均一致。
,因此所有智能体状态达到平均一致。
当G是无向连通图,则
和
成立,其中
为无向图G
的拉普拉斯矩阵,
为对应的特征值序列。
类似于定理1的推导,可以进一步得出定理2。
定理2. 假设无向图是连通的,对所有的
,如果存在
,使得如下条件满足,
则所有智能体将实现平均一致。
注1. 在 [19] 中,Wang等基于跟随者具有无向拓扑图研究了具有时变时滞的一阶领导者–跟随系统,所设计了的事件触发条件为
(13)
定理1和2采用事件触发条件(4),对无领导者的具有时变时滞的一阶多智能体系统进行研究。
我们通过比较事件触发条件(4)和注1中提到的条件(13),可以进一步提出一种混合式事件触发条件:
(14)
其中
。
定理3. 假设有向图是强连通平衡的,对所有的
,如果存在
,使得如下条件满足,
其中
,则所有智能体将实现平均一致。
证明:
情形1. 如果(11)成立,由定理1可以得出相关结论。
情形2.
(15)
由(15),可以得到
其中
。
由Young不等式可以得到
因此有
(16)
由(12)和(16)可以得出,
余下部分证明与定理1中证明类似,故省略之。
类似于定理3的推导,可以进一步得出定理4。
定理4. 假设无向图是连通的,对所有的
,如果存在
,使得如下条件满足,
其中
,则所有智能体将实现平均一致。
注2. 在 [17] 中,Liu等研究了具有固定时滞的一阶系统的一致性问题,分别考虑了有向图和无向图两种情形。本文在其基础上,采用周期采样和事件混合控制的方法对具有时变时滞的一阶多智能体系统进行研究。
4. 数值模拟
本部分将通过仿真实例来说明所得结果的有效性。
考虑由5个智能体组成的多智能体系统,为了与 [17] 形成比较,我们采用了无向的通信拓扑图,通信拓扑图如图1所示,将5个智能体在通讯拓扑图中用1、2、3、4、5标记。
图1是无向连通的,设各边的权重为1,其对应的拉普拉斯矩阵为
拉普拉斯矩阵的最大特征值
为2.39。假设智能体的初始状态为
,取智能体的事件检测器的参数
为0.3,所有智能体的采样周期
,通讯时滞
是关于h的函数变量,假设
,显然
,
。
图2给出了基于一致性协议(2)和事件触发条件(4)的系统(1)的智能体演变状态,从图2可以看出
系统达到了一致,所有智能体的状态趋于初始状态平均值
,这证明了定理2结果的有
效性。
接下来,我们将对不同的事件触发条件进行比较,图3、图4、图5分别展示了在(4)、(13)、(14)下的智能体的事件触发时刻。

Figure 3. Event-triggering time instants under (4)
图3. 智能体在条件(4)下的触发时刻
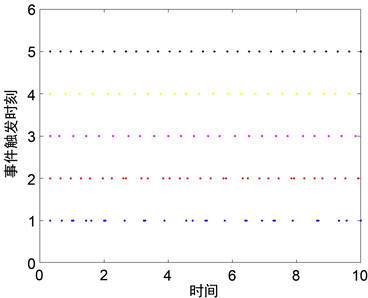
Figure 4. Event-triggering time instants under (13)
图4. 智能体在条件(13)下的触发时刻
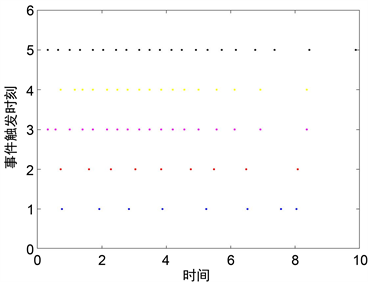
Figure 5. Event-triggering time instants under (14)
图5. 智能体在条件(14)下的触发时刻
根据上面三图我们可以看出,在事件触发条件(14)下,事件触发次数明显减少。所以,事件触发条件(14)优于(4)、(13)。
5. 结论
本文研究了具有变时滞的一阶多智能体系统平均一致性问题,通过利用周期采样数据,智能体的事件触发条件仅在采样时刻被检验。除提出一种不同于已有文献中的事件触发条件外,还设计了一种混合事件触发条件,对已有工作做了改进,得出了保证多智能体系统最终实现平均一致性的相关结论。