1. 引言
随着网络时代的到来,线上教学应运而生,使得学生足不出户就能通过网络高效便捷地学习知识。目前市场线上教学平台多种多样,但学生的需求会随着年级、家庭、成绩、环境等因素的变化而变化,在学生给出需求测度时可能会存在模糊性的情况。例如在评价网络安全时使用“还好、能接受”等诸如此类的语言评价,这种语言模糊性很大程度会使决策的不确定性增加,因此模糊多属性决策也由之受到越来越多学者的关注。1965年,美国控制论专家Zadeh [1] 通过将经典集合的特征函数拓展为隶属函数,率先提出了模糊集的概念,以描述生活中众多亦此亦彼的模糊性现象。但是,模糊集无法刻画非隶属度与犹豫度,即模糊集不能完整刻画决策问题的所有信息。为此,Atanassov [2] 在模糊集的基础上引入非隶属度,提出了直觉模糊集。考虑到决策者在决策时经常会在若干个可能值之间犹豫不决,Torra [3] 提出了犹豫模糊集的概念,其隶属度包含几个可能取值。然而,犹豫模糊集只考虑了隶属度多种可能取值的情况,忽略了非隶属度的重要性。因此,Zhu和Xu [4] 在直觉模糊集和犹豫模糊集的基础上,提出了对偶犹豫模糊集,其隶属度与非隶属度都包含若干种可能取值,能更准确地表达决策者的犹豫不决。由于对偶犹豫模糊集具有上述诸多优越性,学者们纷纷探究其在决策科学中的应用。例如,汪永玲,冯向前,张华荣 [5] 基于对偶犹豫模糊语言]研究了属性权重未知情形下的多属性决策问题。
算子集成理论在多属性决策中具有重要意义。由于多属性决策的过程中需要按照一定的方法对已有信息进行集成,对于算子的研究显得尤为重要。在此之前,杜玉琴 [6]、侯福均 [7] 和翟玉冰 [8] 已在直觉背景研究过Frank集成算子运算法则及其性质。在犹豫模糊环境下,梁玉英 [9]、马庆功 [10] 和赵晓冬 [11] 等提出了一系列犹豫模糊Frank集成算子。相比较而言,在处理多属性决策问题时,由于Frank算子可以根据不同的参数来解决不同类型的多属性决策问题,具有较强的兼容性。因此Frank算子比Choquet算子 [12] 和Power算子 [13] [14] 更灵活,应用更为广泛。目前,关于Frank算子应用于对偶犹豫模糊语言变量还比较少见,因此,对偶犹豫模糊语言Frank集成算子具有重要的研究意义。
本文基于对偶犹豫模糊语言环境下的运算规则、得分函数、精确函数和大小比较方法,定义了对偶犹豫模糊语言环境下Frank算子的运算规则,提出了对偶犹豫模糊语言Frank加权算术平均算子、对偶犹豫模糊语言Frank有序加权算术平均算子,研究了这些算子的有界性、单调性和交换性等性质,并证明参数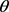 逼近1时,对偶犹豫模糊语言Frank加权算术平均算子退化为对偶犹豫模糊语言加权算术平均算子。最后,将对偶犹豫模糊语言Frank加权算术平均算子应用于对偶犹豫模糊语言环境下的多属性决策问题。
逼近1时,对偶犹豫模糊语言Frank加权算术平均算子退化为对偶犹豫模糊语言加权算术平均算子。最后,将对偶犹豫模糊语言Frank加权算术平均算子应用于对偶犹豫模糊语言环境下的多属性决策问题。
2. 预备知识
定义1 [4]:设X是一个非空集合,则X上的对偶犹豫模糊语言集(Dual Hesitant Fuzzy Linguistic Set, DHFLS)定义为
(1)
式中,
,
表示
的可能隶属度,
表示
的可能非隶属度,并且
,
,
时,有
,
,
,
。
定义2 [15]:设
和
是两个给定的对偶犹豫模糊语言变量,则可定
义如下运算
1) 数乘运算
,
;
2) 幂运算
,
;
3) 和运算
;
4) 积运算
。
在多属性决策过程中,语言集的比较一直是关注重点。在研究对偶犹豫模糊语言变量时,得分函数和精确函数能有效解决其大小比较问题。
定义3:设
为任意的对偶犹豫模糊语言变量,其得分函数
和精确函数
分别定义为
(2)
(3)
式中,
为语言评价集的元素个数,
,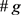 分别表示集合h和集合g中元素的个数。显然有
,
,并且有
越大,d越优。
分别表示集合h和集合g中元素的个数。显然有
,
,并且有
越大,d越优。
定义4:设
和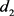 是两个给定的DHFLS,则
是两个给定的DHFLS,则
1) 若
,则
;
2) 若
,那么当
时,
;当
时,
。
3. 对偶犹豫模糊语言Frank集成算子
3.1. 对偶犹豫模糊语言Frank算子的运算规则
根据对偶犹豫模糊语言变量、Frank-T范数和Frank-S范数 [16],定义对偶犹豫模糊语言环境下Frank算子的运算法则如下。
定义6:设
和
是两个给定的DHFLS,基于对偶犹豫模糊语言Frank
算子的运算规则定义如下
,
; (6)
,
; (7)
; (8)
. (9)
易证上述计算结果仍为对偶犹豫模糊语言变量。
为了实现多个对偶犹豫模糊语言变量的集结,本文提出了基于该语言集的加权算术平均算子、有序加权算术平均算子。
3.2. 对偶犹豫模糊语言Frank加权算术平均算子
定义7:设
为一组任意对偶犹豫模糊语言变量,
是
的权重向量,满足
且
,那么对偶犹豫模糊语言Frank加权算术平均算子(DHFLFWA)定
义如下
定理1:设
为一组任意对偶犹豫模糊语言变量,
是d的权重向量,满足
且
,那么运用DHFLFWA算子计算得到的结果仍然是对偶犹豫模
糊语言变量,并且
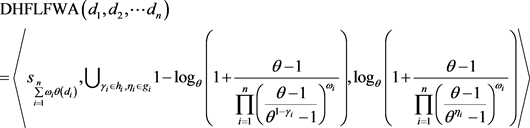 (10)
(10)
易用数学归纳法证明等式(10)成立,此外,DHFLFWA算子也具有有界性,如定理2所示。
定理2:(有界性)设
为一组任意对偶犹豫模糊语言变量,若
,
,
,
,
,
,则
此外,易知DHFLFWA也算子具有幂等性和单调性,如定理3和定理4所示。
定理3:(单调性)设
和
为两组对偶犹豫模糊语言变量,若对于任意的
,有
,那么
。
下面研究DHFLFWA算子中参数
的性质。
推论1 当
时,对偶犹豫模糊语言Frank加权算术平均算子(DHFLFWA)就转化为对偶犹豫模糊语言加权算术平均算子(DHFLWAA):
(11)
证明 由定义2,
可知若
为严格单调递减的加性算子时,
,于是有
可以得到
3.3. 对偶犹豫模糊语言Frank有序加权算术平均算子
定义8:设
为一组任意对偶犹豫模糊语言变量,
是
的位置权重向量,满足
且
,
为
中第i大的元素。对偶犹豫模糊语言Frank有序加权算术平均算子(DHFLFOWA)定义如下
(12)
显然,与对偶犹豫模糊语言Frank加权算术平均算子(DHFLFWA)类似,对偶犹豫模糊语言Frank有序加权算术平均算子(DHFLFOWA)也具有有界性和单调性。此外,对偶犹豫模糊语言Frank有序加权算术平均算子(DHFLFOWA)还具有交换性。
定理4:(交换性)设
为一组任意对偶犹豫模糊语言变量,如果
是
的任意位置交换,则有
.
4. 基于对偶犹豫模糊语言Frank集成算子的多属性决策方法
对于一个多属性决策问题,假设
为一个给定的方案集合,
为属性集合,其对应的属性权重为
,满足
且
。现邀请几位
专家对已有方案进行综合评估,由于专家评估带有个人偏好且不唯一,为更好的描述专家综合评估值,属性值采用对偶犹豫模糊语言变量的形式表达:方案
在属性
下的属性值为
,其中s为给定语言评价集
,由此,决策者构建的决策矩阵为
。针对上述问题,本文提出了一种基于对偶犹豫模糊语言Frank加权平均
算子的多属性决策方法,具体步骤如下:
步骤1 规范化决策信息。对于效益型,其属性值保持不变,即
;对于成本型,需要转化为
,其中
,
,即
步骤2 基于得到的规范化矩阵
,集成各方案的属性值。运用对偶犹豫模糊语言Frank加权算术平均算子(DHFLFWA)对决策矩阵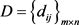 中的第i行进行集成,求得方案
的综合属性值
。
中的第i行进行集成,求得方案
的综合属性值
。
(13)
步骤3 在步骤2 的基础上得到综合属性值后,运用得分函数公式(2)和精确函数公式(3)计算
的得分函数值
和精确函数
值。
步骤4 根据定义4,对各个备选方案进行综合性能的排序。得分函数值越大,方案的性能值越好;当得分函数值相等时,继续比较精确函数值,精确函数值越大,方案性能越好,以此选出最优方案。
5. 实证分析
某教育机构开办了网络线上课堂,使得学生能利用电脑、平板、手机等电子通讯设备进行线上学习,丰富了课堂形式,能按自己需投求选择适合自己的课程。经过前期试运行,挑选了关注度较高的三个学生需求测度:
:网络服务器(包括网络安全性、稳定性等)
:功能设计(包括线上答疑、课程录播等)
:教学质量(包括老师资历、课堂形式等)
由于学生的年级、成绩、环境等原因,对上述三个需求会有所不同。故采取问卷调查形式,对三类学生进行调查分析,
为后进生,
为中等生,
为尖子生,挑选出具有代表性的问卷结果。由于问卷结果均为自然语言,如“尚可,一般,很好”等诸如此类的自然语言,因此为更好地保留学生需求的原始信息,需要由相关专家对问卷进行评估,均采用对偶犹豫模糊语言对顾客需求进行表示,属性权重向量为
,语言评价集为
决策者给出各方案的属性值如表1所示。

Table 1. Attribute values of each scheme
表1. 各方案的属性值
步骤1 由于3个需求均为效益型,因此无需进行规范化处理。
步骤2 运用对偶犹豫模糊语言Frank加权算术平均算子(DHFLFWA)对信息进行集成。由于对偶犹豫模糊语言Frank加权算术平均算子(DHFLFWA)形式会随参数而变,为了更好的选择备选方案,本文将列举5个具有代表性的参数值分别进行计算。
步骤3 计算各个备选方案综合属性值的得分函数值。
1) 当
时,有
,
,
。
2) 当
时,有
,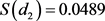 ,
。
,
。
3) 当
时,有
,
,
。
4) 当
时,有
,
,
。
5) 当
时,有
,
, 。
。
步骤4 根据定义4,对各个方案进行排序,排序结果都为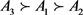 ,故
教学质量是三类学生最关注的需求,因此线上教学平台可针对这一需求加大整改力度。
,故
教学质量是三类学生最关注的需求,因此线上教学平台可针对这一需求加大整改力度。
通过分析发现,选取不同的参数值,计算得到的属性值虽然不同,但最终排序的结果相同。为了进一步说明本文提出的算法具有可靠性、合理性,下面将与文献 [17] 中提出的对偶犹豫模糊语言加权算术平均算子(DHFLWAA)进行对比分析。具体决策过程与对偶犹豫模糊语言Frank加权算术平均算子(DHFLFWA)类,有
,
,
。利用综合属性值对应的得分函数对备选方案进行排序,结果如表2所示。
通过观察表2中的排序结果可以发现,运用本文和文献 [17] 两种不同的算子计算得到的排序结果相同:
,即学生需求关注最高点为教学质量,说明本文构建的多属性决策方法具有合理性。此外,本文提出的对偶犹豫模糊语言Frank加权算术平均算子(DHFLFWA)具有可变参数
,这将能满足决策者的不同需要,使得决策过程更灵活多变,因此决策更具一般性。本文提出对偶犹豫模糊语言Frank集结算子是有效且灵活的。

Table 2. Sorting results calculated by different operators
表2. 利用不同算子计算得到的排序结果
6. 结论
本文基于语言评价集、对偶犹豫模糊集和Frank S-范数与Frank T-范数,给出了对偶犹豫模糊语言变量Frank集结算子,即对偶犹豫模糊语言Frank加权算术平均算子、对偶犹豫模糊语言Frank有序加权算术平均算子,并对两种算子的有界性、幂等性、单调性和交换性等性质加以研究。之后,给出了对偶犹豫模糊语言Frank集结算子具体的决策步骤,将对偶犹豫模糊语言Frank加权算术平均算子应用于多属性决策问题。最后,通过实例并与文献 [17] 中提出的DHFLWAA算子做对比分析,表明本文提出的对偶犹豫模糊语言Frank集结算子具有可行性和有效性。
基金项目
江西省教育厅科技重点项目(GJJ171109)。