正则化交替方向乘子算法求解非凸不可分离问题

Regualized Alternating Direction Method of Multiplies for Nonseparable Nonconvex Problem

摘要: 本文作者提出了一种新的正则化交替方向乘子法来解决非凸优化问题，在不要求正则项严格凸的情况下证明了算法的全局收敛性，在增广拉格朗日函数满足KL性质的条件下，证明了算法的强收敛性，并且通过应用于Lasso模型求解，证明了算法的有效性。

Abstract: In this paper, we propose a new regularized alternating direction method of multipliers to solve the non-convex optimization problem. We prove the global convergence of the algorithm without requiring the strict convexity of the regular term. Under the condition that the augmented Lagrangian function satisfies KL function, the strong convergence of the algorithm is proved, and the effectiveness of the algorithm is proved by applying it to the Lasso model.

1. 引言

本文我们考虑具有如下形式的非凸不可分离问题

$\begin{array}{l}\min f\left(x\right)+g\left(y\right)+H\left(x,y\right)\\ \text{s}\text{.t}.Ax+y=b\end{array}$ (1.1)

其中， $f:R^n\to R\cup \left\{+\infty \right\}$ 是正常下班连续函数， $g:R^m\to R$ 为连续可微函数，且 $\nabla g$ 利普西茨连续(利普西茨常数 $L_1>0$ )； $H:R^n\times R^m\to R$ 是光滑函数，且x和y是不可分离的。 $A\in R^{m\times n}$ 是给定的矩阵， $b\in R^m$ 是一个向量。问题(1.1)的一种特殊形式如下

$\begin{array}{l}\min f\left(x\right)+\text{g}\left(y\right)\\ \text{s}\text{.t}\text{.}Ax+y=b\end{array}$ (1.2)

交替方向乘子法(ADMM)在解决问题(1.2)方面有许多的研究，它的迭代格式如下

$\{\begin{array}{l}{x}^{k+1}\in \arg {\min }_x\left\{L_{\beta }\left(x,y^k,{\lambda }^k\right)\right\},\\ y^{k+1}\in \arg {\min }_y\left\{L_{\beta }\left(x^{k+1},y,{\lambda }^k\right)\right\},\\ {\lambda }^{k+1}={\lambda }^k-\beta \left(A{x}^{k+1}+y^{k+1}-b\right).\end{array}$ (1.3)

其中， $L_{\beta }(·)$ 为问题(1.2)的增广拉格朗日函数。在凸情形下，ADMM算法的研究已经比较完善。而在非凸的情况下，其收敛性研究则更具挑战。

针对问题(1.2)，Guo等 [1] [2] 考虑利用经典的ADMM算法解决非凸最优化问题，证明了其收敛性，并且提出了一些充分条件保证了算法的超线性和线性收敛速率。Li和Ting [3] 提出了一种近似ADMM算法来解决非凸非光滑优化问题，证明了当罚参数足够大且生成的序列有聚点时，非凸问题收敛到稳定点。

然而，针对问题(1.1)，由于函数H的存在，即使问题是凸的情况，对ADMM算法收敛性的研究还处于初期。Guo和Wang [4] 提出了一种广义的ADMM算法，证明了在增光拉格朗日函数满足KL不等式的情况下算法的收敛性。Chen等 [5] 在耦合函数g是二次函数的情况下，分析了ADMM的收敛性。Gao和Zhang [6] 考虑了函数H是光滑函数以及函数 $f,g$ 是凸函数的情况。通过假设 $\nabla g$ 是利普希茨连续以及h强凸，证明了由ADMM算法生成的序列收敛到问题(1.4)的最优解。

针对问题(1.1)，本文通过结合Guo [4] 和Jian [7] 的方法，提出了一种正则化交替方向乘子法(RADMM)，形式如下

$\{\begin{array}{l}{x}^{k+1}\in \arg {\min }_x\left\{L_{\beta }\left(x,y^k,{\lambda }^k\right)\right\}+\frac{1}{2}{\Vert x-x^k\Vert }_G^2,\\ y^{k+1}\in \arg {\min }_y\left\{L_{\beta }\left(x^{k+1},y,{\lambda }^k\right)\right\},\\ {\lambda }^{k+1}={\lambda }^k-\beta \left(A{x}^{k+1}+y^{k+1}-b\right).\end{array}$ (1.4)

其中， $L_{\beta }(·)$ 为问题(1.1)的增广拉格朗日函数，定义如下

$L_{\beta }\left(x,y,\lambda \right)=f\left(x\right)+g\left(y\right)+H\left(x,y\right)-\langle \lambda ,Ax+y-b\rangle +\frac{\beta }{2}{\Vert Ax+y-b\Vert }^2$ (1.5)

2. 预备知识

本节我们给出一些本文理论分析所需要的概念和性质。

对于任意 $x\in R^n$ 是函数f的极小值点的必要条件是 $0\in \partial f\left(x\right)$，满足这个条件的点成为稳定点，函数f的稳定点集记作 $critf$。

引理2.1 [8] [9]： $h:R^m\to R$ 是连续可微函数，且 $\nabla h$ 是关于常数L利普希茨连续的，那么对于任意的 $x,y\in R^n$，有

$\left|h\left(y\right)-h\left(x\right)-\langle \nabla h\left(x\right),y-x\rangle \right|\le \frac{L}{2}{\Vert y-x\Vert }^2.$

引理2.2：( [9] Kurdyka-Lojasiewicz inequality)设函数 $f:R^n\to R\cup \left\{+\infty \right\}$ 是恰当下半连续函数，对于 $-\infty <{\eta }_1<{\eta }_2<+\infty$，令 $\left[{\eta }_1<f<{\eta }_2\right]:=\left\{x\in R^n:{\eta }_1<f\left(x\right)<{\eta }_2\right\}$。

若存在 $\eta \in (0,+\infty ]$， $x^{*}$ 的领域U以及一个连续的凹函数 $\phi :\left[0,\eta \right)\to R_{+}$，满足如下条件：

i) $\phi \left(0\right)=0$

ii) $\phi$ 在 $\left(0,\eta \right)$ 连续可微且在0处连续

iii) ${\phi }^{\prime }\left(s\right)>0,\forall s\in \left(0,\eta \right)$

iv) 对所有的 $x\in U\cap \left[f\left(x^{*}\right)<f<f\left(x^{*}\right)+\eta \right]$，有如下Kurdyka-Lojasiewicz不等式成立：

${\phi }^{\prime }\left(f\left(x\right)-f\left(x^{*}\right)\right)d\left(0,\partial f\left(x\right)\right)\ge 1.$

则称函数f在 $x^{*}\in dom\partial f$ 上满足KL性质。

引理2.3：( [9] Uniformized KL property) $\Omega$ 是紧集，设函数 $f:R^n\to R\cup \left\{+\infty \right\}$ 是恰当下半连续函数。假设f在 $\Omega$ 上是常数并且在 $\Omega$ 上的每个点满足KL性质，那么存在 $\epsilon >0,\eta >0$ 以及 $\phi \in {\Phi }_{\eta }$，使得对于任意的 $\tilde{x}\in \Omega$ 以及 $x\in \left\{x\in R^n:d\left(x,\Omega \right)<\epsilon \right\}\cap \left\{f\left(\tilde{x}\right)<f<f\left(\tilde{x}\right)+\eta \right\}$，有

${\phi }^{\prime }\left(f\left(x\right)-f\left(\tilde{x}\right)\right)d\left(0,\partial f\left(x\right)\right)\ge 1.$

3. 收敛性分析

本节，我们令 ${\omega }^k=\left\{x^k,y^k,{\lambda }^k\right\}$， $v^k:=\left(x^k,y^k\right)$ 其中 $\left\{{\omega }^k\right\}$ 为算法(1.4)生成的序列，并假设有界。

由(1.4)的最优性，有

$\{\begin{array}{l}0\in \partial f\left(x^{k+1}\right)+{\nabla }_{x}H\left(x^{k+1},y^k\right)-A^{{\rm T}}{\lambda }^k+\beta A^{{\rm T}}\left(A{x}^{k+1}+y^k-b\right)+G\left(x^{k+1}-x^k\right),\\ 0=\nabla g\left(y^{k+1}\right)+{\nabla }_{y}H\left(x^{k+1},y^{k+1}\right)-{\lambda }^k+\beta \left(A{x}^{k+1}+y^{k+1}-b\right),\\ {\lambda }^{k+1}={\lambda }^k-\beta \left(A{x}^{k+1}+y^{k+1}-b\right).\end{array}$ (3.1)

即

$\{\begin{array}{l}{A}^{{\rm T}}{\lambda }^{k+1}+\beta A^{{\rm T}}\left(y^{k+1}-y^k\right)-{\nabla }_{x}H\left(x^{k+1},y^k\right)-G\left(x^{k+1}-x^k\right)\in \partial f\left(x^{k+1}\right),\\ \nabla g\left(y^{k+1}\right)={\lambda }^{k+1}-{\nabla }_{y}H\left(x^{k+1},y^{k+1}\right),\\ {\lambda }^{k+1}={\lambda }^k-\beta \left(A{x}^{k+1}+y^{k+1}-b\right).\end{array}$ (3.2)

贯穿本文，我们做出如下假设。

假设3.1令 $f:R^n\to R\cup \left\{+\infty \right\}$ 是弱凸函数，常数 $\omega >0$ ； $g:R^m\to R$ 是连续可微函数，它的梯度 $\nabla g$ 是利普希茨连续的，其利普希茨常数 $L_1>0$ ； $H:R^n\times R^m\to R$ 是光滑函数。假设问题(1.1)满足下列条件：

i) $\Vert {\nabla }_{y}H\left(x,y\right)-{\nabla }_{y}H\left(x,\tilde{y}\right)\Vert \le L_2\left(x\right)\Vert y-\tilde{y}\Vert ,\forall y,\tilde{y}\in R^n$

$\Vert {\nabla }_{x}H\left(x,y\right)-{\nabla }_{x}H\left(\tilde{x},y\right)\Vert \le L_3\left(y\right)\Vert x-\tilde{x}\Vert ,\forall x,\tilde{x}\in R^n$

ii) $\nabla H$ 在 $R^n\times R^m$ 的有界子集上是利普希茨连续的。换句话说，对于每个有界子集 $B_1\times B_2\subseteq R^n\times R^m$，存在 $M>0$，使得对于所有的 $\left(x_i,y_i\right)\in B_1\times B_2,i=1,2$，

$\Vert {\nabla }_{x}H\left(x_1,y_1\right)-{\nabla }_{x}H\left(x_2,y_2\right),{\nabla }_{y}H\left(x_1,y_1\right)-{\nabla }_{y}H\left(x_2,y_2\right)\Vert \le M\Vert \left(x_1-y_1,x_2-y_2\right)\Vert$

iii) 存在 $L_2,L_3>0$，使得 $\sup \left\{L_2\left(x^k\right):k\in N\right\}\le L_2,\sup \left\{L_3\left(x^k\right):k\in N\right\}\le L_3$。

引理3.1

$L_{\beta }\left(x^{k+1},y^{k+1},{\lambda }^{k+1}\right)-L_{\beta }\left(x^k,y^k,{\lambda }^k\right)\le \delta {\Vert v^{k+1}-v^k\Vert }^2-\frac{1}{2}{\Vert x^{k+1}-x^k\Vert }_G^2.$ (3.3)

证明：由增光拉格朗日的定义及(3.2c)式可得

$\begin{array}{c}{L}_{\beta }\left(x^{k+1},y^{k+1},{\lambda }^{k+1}\right)=L_{\beta }\left(x^{k+1},y^{k+1},{\lambda }^k\right)+\langle {\lambda }^{k+1}-{\lambda }^k,A{x}^{k+1}+y^{k+1}-b\rangle \\ =L_{\beta }\left(x^{k+1},y^{k+1},{\lambda }^k\right)+\frac{1}{\beta }{\Vert {\lambda }^k-{\lambda }^{k+1}\Vert }^2\end{array}$ (3.4)

且

$\begin{array}{l}{L}_{\beta }\left(x^{k+1},y^{k+1},{\lambda }^k\right)-L_{\beta }\left(x^{k+1},y^k,{\lambda }^k\right)\\ =g\left(y^{k+1}\right)-g\left(y^k\right)+H\left(x^{k+1},y^{k+1}\right)-H\left(x^{k+1},y^k\right)-\langle {\lambda }^k,y^{k+1}-y^k\rangle \\ +\frac{\beta }{2}{\Vert A{x}^{k+1}+y^{k+1}-b\Vert }^2-\frac{\beta }{2}{\Vert A{x}^{k+1}+y^k-b\Vert }^2\end{array}$ (3.5)

由引理2.1及(3.2b)式可得

$g\left(y^{k+1}\right)-g\left(y^k\right)\le \langle {\lambda }^{k+1}-{\nabla }_{y}H\left(x^{k+1},y^{k+1}\right),y^{k+1}-y^k\rangle +\frac{L_1}{2}{\Vert y^k-y^{k+1}\Vert }^2$ (3.6)

又因为 ${\nabla }_{y}H\left(x^{k+1},\cdot \right)$ 是关于常数 $L_2\left(x^{k+1}\right)$ 利普希茨连续的，则

$H\left(x^{k+1},y^{k+1}\right)-H\left(x^{k+1},y^k\right)\le \langle {\nabla }_{y}H\left(x^{k+1},y^{k+1}\right),y^{k\text{+1}}-y^k\rangle -\frac{L_2\left(x^{k+1}\right)}{2}{\Vert y^{k+1}-y^k\Vert }^2.$ (3.7)

将(3.6)式和(3.7)式代入(3.5)式得到

$\begin{array}{l}{L}_{\beta }\left(x^{k+1},y^{k+1},{\lambda }^k\right)-L_{\beta }\left(x^{k+1},y^k,{\lambda }^k\right)\\ \le \langle {\lambda }^{k+1}-{\lambda }^k,y^{k+1}-y^k\rangle +\frac{L_1}{2}{\Vert y^k-y^{k+1}\Vert }^2+\frac{L_2\left(x^{k+1}\right)}{2}{\Vert y^{k+1}-y^k\Vert }^2\\ \text{+}\frac{\beta }{2}{\Vert A{x}^{k+1}+y^{k+1}-b\Vert }^2-\frac{\beta }{2}{\Vert A{x}^{k+1}+y^k-b\Vert }^2.\end{array}$ (3.8)

由(3.2)的第三个式子，有

$A{x}^{k+1}+y^{k+1}-b=\frac{1}{\beta }\left({\lambda }^k-{\lambda }^{k+1}\right)$ (3.9)

则

$A{x}^{k+1}+y^k-b=\frac{1}{\beta }\left({\lambda }^k-{\lambda }^{k+1}\right)-\left(y^{k+1}-y^k\right)$ (3.10)

因此，将(3.9)和(3.10)代入(3.8)，得到

$L_{\beta }\left(x^{k+1},y^{k+1},{\lambda }^k\right)-L_{\beta }\left(x^{k+1},y^k,{\lambda }^k\right)\le \frac{L_1+L_2\left(x^{k+1}\right)-\beta }{2}{\Vert y^{k+1}-y^k\Vert }^2.$ (3.11)

又由(3.2b)可知

$\begin{array}{c}{\Vert {\lambda }^{k+1}-{\lambda }^k\Vert }^2=\Vert \nabla g\left(y^{k+1}\right)+{\nabla }_{y}H\left(x^{k+1},y^{k+1}\right)-{\nabla g\left(y^k\right)-{\nabla }_{y}H\left(x^k,y^k\right)\Vert }^2\\ \le 2{\Vert \nabla g\left(y^{k+1}\right)-\nabla g\left(y^k\right)\Vert }^2+2{\Vert {\nabla }_{y}H\left(x^{k+1},y^{k+1}\right)-{\nabla }_{y}H\left(x^k,y^k\right)\Vert }^2\\ \le 2L_1^2\Vert y^{k+1}-{y^k\Vert }^2+2M^2{\Vert x^{k+1}-x^k\Vert }^2+2M^2{\Vert y^{k+1}-y^k\Vert }^2\\ =\left(2L_1^2+2M^2\right){\Vert y^{k+1}-y^k\Vert }^2+2M^2{\Vert x^{k+1}-x^k\Vert }^2.\end{array}$ (3.12)

其中，第二个不等式由 $\nabla g$ 的利普西茨连续性和假设3.1的(ii)得到。将(3.12)式代入(3.4)式，得到

$L_{\beta }\left(x^{k+1},y^{k+1},{\lambda }^{k+1}\right)-L_{\beta }\left(x^{k+1},y^{k+1},{\lambda }^k\right)\le \frac{\left(2L_1^2+2M^2\right)}{\beta }{\Vert y^{k+1}-y^k\Vert }^2+\frac{2M^2}{\beta }{\Vert x^{k+1}-x^k\Vert }^2.$ (3.13)

又因为 $x^{k+1}$ 是(1.4a)的最优解，所以

$L_{\beta }\left(x^{k+1},y^k,{\lambda }^k\right)\le L_{\beta }\left(x^k,y^k,{\lambda }^k\right)-\frac{1}{2}{\Vert x^{k+1}-x^k\Vert }_G^2,$ (3.14)

结合(3.11)，(3.13)及(3.14)，有

$\begin{array}{l}{L}_{\beta }\left(x^{k+1},y^{k+1},{\lambda }^{k+1}\right)\\ \le L_{\beta }\left(x^k,y^k,{\lambda }^k\right)+(\frac{\left(2L_1^2+2M^2\right)}{\beta }+\frac{L_1+L_2\left(x^{k+1}\right)-\beta }{2}){\Vert y^{k+1}-y^k\Vert }^2\\ +\frac{2M^2}{\beta }{\Vert x^{k+1}-x^k\Vert }^2-\frac{1}{2}{\Vert x^{k+1}-x^k\Vert }_G^2\le \delta {\Vert v^{k+1}-v^k\Vert }^2-\frac{1}{2}{\Vert x^{k+1}-x^k\Vert }_G^2.\end{array}$

在最后一个不等式中，令

$\delta :=\min \left\{\frac{\left(2L_1^2+2M^2\right)}{\beta }+\frac{L_1+L_2\left(x^{k+1}\right)-\beta }{2},\frac{2M^2}{\beta }\right\}$

显然， $\delta >0$。引理获证。

引理3.2： ${\displaystyle \underset{k=0}{\overset{+\infty }{\sum }}{\Vert {\omega }^{k+1}{\omega }^k\Vert }^2}<+\infty$

证明：由于序列 ${\left\{{\omega }^k\right\}}_{k\in N}$ 是有界的，则存在收敛子列 ${\left\{{\omega }^{k_j}\right\}}_{j\in N}$ 且 ${\omega }^{k_j}\to {\omega }^{*}$。由h和g的连续性和f的下半连续性可知 $L_{\beta }(\cdot )$ 下班连续，从而

$L_{\beta }\left({\omega }^{*}\right)\le \underset{j\to \infty }{\lim \inf }{L}_{\beta }\left({\omega }^{k_j}\right).$ (3.15)

因此序列 ${\left\{L_{\beta }\left({\omega }^{k_j}\right)\right\}}_{j\in N}$ 有下界，又由引理3.1知 ${\left\{L_{\beta }\left({\omega }^{k_j}\right)\right\}}_{j\in N}$ 单调递减，所以 ${\left\{L_{\beta }\left({\omega }^{k_j}\right)\right\}}_{j\in N}$ 收敛，此外 ${\left\{L_{\beta }\left({\omega }^k\right)\right\}}_{j\in N}$ 也是收敛的，且 $L_{\beta }\left({\omega }^k\right)\ge L_{\beta }\left({\omega }^{*}\right)$。由引理3.1可得

${\displaystyle \underset{k=0}{\overset{m}{\sum }}\delta {\Vert v^{k+1}-v^k\Vert }^2-\frac{1}{2}{\Vert x^{k+1}-x^k\Vert }_G^2\le L_{\beta }\left({\omega }^0\right)-}{L}_{\beta }\left({\omega }^{m+1}\right)\le L_{\beta }\left({\omega }^0\right)-L_{\beta }\left({\omega }^{*}\right)<+\infty .$

由于 $\delta >0$， $G\succcurlyeq 0$

${\displaystyle \underset{k=0}{\overset{+\infty }{\sum }}{\Vert v^{k+1}-v^k\Vert }^2}<+\infty ,{\displaystyle \underset{k=0}{\overset{+\infty }{\sum }}{\Vert x^{k+1}-x^k\Vert }_G^2}.$ (3.16)

因此，

${\displaystyle \underset{k=0}{\overset{+\infty }{\sum }}{\Vert x^{k+1}-x^k\Vert }^2}<+\infty ,{\displaystyle \underset{k=0}{\overset{+\infty }{\sum }}{\Vert y^{k+1}-y^k\Vert }^2}<+\infty .$

则由(3.12)式可知 ${\displaystyle \underset{k=0}{\overset{+\infty }{\sum }}{\Vert {\lambda }^{k+1}-{\lambda }^k\Vert }^2}<+\infty$。

因此 ${\displaystyle \underset{k=0}{\overset{+\infty }{\sum }}{\Vert {\omega }^{k+1}-{\omega }^k\Vert }^2}<+\infty$。

引理3.3：存在 $\eta >0$，使得 $d\left(0,\partial L_{\beta }\left({\omega }^{k+1}\right)\right)\le \eta \Vert v^{k+1}-v^k\Vert$

证明：根据 $L_{\beta }(\cdot )$ 的定义知

$\{\begin{array}{l}{\partial }_x{L}_{\beta }\left({\omega }^{k+1}\right)=\partial f\left(x^{k+1}\right)+{\nabla }_{x}H\left(x^{k+1},y^{k+1}\right)-A^{{\rm T}}{\lambda }^k+\beta A^{{\rm T}}\left(A{x}^{k+1}+y^{k+1}-b\right),\\ {\partial }_y{L}_{\beta }\left({\omega }^{k+1}\right)=\nabla g\left(y^{k+1}\right)+{\nabla }_{y}H\left(x^{k+1},y^{k+1}\right)-{\lambda }^{k+1}+\beta \left(A{x}^{k+1}+y^{k+1}-b\right),\\ {\partial }_{\lambda }{L}_{\beta }\left({\omega }^{k+1}\right)=-\left(A{x}^{k+1}+y^{k+1}-b\right).\end{array}$ (3.17)

结合(3.17)及(3.2)

$\{\begin{array}{l}{A}^{{\rm T}}\left({\lambda }^k-{\lambda }^{k+1}\right)+\beta A^{{\rm T}}\left(y^{k+1}-y^k\right)+{\nabla }_{x}H\left(x^{k+1},y^{k+1}\right)-{\nabla }_{x}H\left(x^{k+1},y^k\right)-G\left(x^{k+1}-x^k\right)\in {\partial }_x{L}_{\beta }\left({\omega }^{k+1}\right)\\ {\lambda }^k-{\lambda }^{k+1}\in {\partial }_y{L}_{\beta }\left({\omega }^{k+1}\right)\\ -\frac{1}{\beta }\left({\lambda }^{k+1}-{\lambda }^k\right)\in {\partial }_{\lambda }{L}_{\beta }\left({\omega }^{k+1}\right)\end{array}$

定义

$\{\begin{array}{l}{\zeta }_x^{k+1}=A^{{\rm T}}\left({\lambda }^k-{\lambda }^{k+1}\right)+\beta A^{{\rm T}}\left(y^{k+1}-y^k\right){\nabla }_{x}H\left(x^{k+1},y^{k+1}\right)-{\nabla }_{x}H\left(x^{k+1},y^k\right)-G\left(x^{k+1}-x^k\right)\\ {\zeta }_y^{k+1}={\lambda }^{k+1}-{\lambda }^k\\ {\zeta }_{\lambda }^{k+1}=-\frac{1}{\beta }\left({\lambda }^{k+1}-{\lambda }^k\right)\end{array}$

则 ${\left({\zeta }_x^{k+1},{\zeta }_y^{k+1},{\zeta }_{\lambda }^{k+1}\right)}^{{\rm T}}\in L_{\beta }\left({\omega }^{k+1}\right)$，且

存在 ${\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4>0$，使得

$\begin{array}{c}\Vert {\left({\zeta }_x^{k+1},{\zeta }_y^{k+1},{\zeta }_{\lambda }^{k+1}\right)}^{{\rm T}}\Vert \le {\eta }_1\Vert x^{k+1}-x^k\Vert +{\eta }_2\Vert y^{k+1}-y^k\Vert +{\eta }_3\Vert {\lambda }^{k+1}-{\lambda }^k\Vert \\ +{\eta }_4\Vert {\nabla }_{x}H\left(x^{k+1},y^{k+1}\right)-{\nabla }_{x}H\left(x^{k+1},y^k\right)\Vert \end{array}$ (3.18)

由假设3.1的(ii)可知

$\Vert {\nabla }_{x}H\left(x^{k+1},y^{k+1}\right)-{\nabla }_{x}H\left(x^{k+1},y^k\right)\Vert \le M\Vert y^{k+1}-y^k\Vert$ (3.19)

由(3.12)式可得

$\Vert {\lambda }^{k+1}-{\lambda }^k\Vert \le \sqrt{\left(2L_1^2+2M^2\right)}\Vert y^{k+1}-y^k\Vert +\sqrt{2}M\Vert x^{k+1}-x^k\Vert$ (3.20)

令 $\eta :=\sqrt{{\left({\eta }_1+\sqrt{2}M{\eta }_3\right)}^2+{\left({\eta }_2+\sqrt{\left(2L_1^2+2M^2\right)}{\eta }_3+M{\eta }_4\right)}^2}$

结合(3.18)，(3.19)，(3.20)，得到

$\begin{array}{c}d\left(0,\partial L_{\beta }\left({\omega }^{k+1}\right)\right)\le \Vert {\left({\zeta }_x^{k+1},{\zeta }_y^{k+1},{\zeta }_{\lambda }^{k+1}\right)}^{{\rm T}}\Vert \\ \le \left({\eta }_1+\sqrt{2}M{\eta }_3\right)\Vert x^{k+1}-x^k\Vert +\left({\eta }_2+\sqrt{\left(2L_1^2+2M^2\right)}{\eta }_3+M{\eta }_4\right)\Vert y^{k+1}-y^k\Vert \\ \le \eta \Vert v^{k+1}-v^k\Vert \end{array}$

引理获证。

引理3.4：记序列 ${\left\{{\omega }^k\right\}}_{k\in N}$ 的所有极限点为 $S\left({\omega }^0\right)$，则

i) $S\left({\omega }^0\right)$ 是一个非空紧集，并且 $d\left({\omega }^k,S\left({\omega }^0\right)\right)\to 0,k\to +\infty$ ；

ii) $S\left({\omega }^0\right)\subset crit{L}_{\beta }$ ；

iii) $L_{\beta }(\cdot )$ 在 $S\left({\omega }^0\right)$ 上取有限值且为常量，且 $\underset{k\in N}{\inf }{L}_{\beta }\left({\omega }^k\right)=\underset{k\to +\infty }{\lim }{L}_{\beta }\left({\omega }^k\right)$。

证明：i) 可由 $S\left({\omega }^0\right)$ 的定义可直接得到。

ii) 对于任意点 $\left(x^{*},y^{*},{\gamma }^{*}\right)\in S\left({\omega }^0\right)$，存在子列 $\left\{\left(x^{k_j},y^{k_j},{\gamma }^{k_j}\right)\right\}\to \left(x^{*},y^{*},{\gamma }^{*}\right),k_j\to +\infty$，

根据增广拉格朗日函数的定义， $x^{k+1}$ 是 $L_{\beta }\left(x,y^k,{\gamma }^k\right)$ 关于变量x的全局最小点，因此由(1.4)第一个式有

$L_{\beta }\left(x^{k+1},y^k,{\gamma }^k\right)\text{+}\frac{1}{2}{\Vert x^{k+1}-x^k\Vert }_G^2\le L_{\beta }\left(x^{*},y^k,{\gamma }^k\right)\frac{1}{2}{\Vert x^{\ast }-x^k\Vert }_G^2.$

又 $L_{\beta }(\cdot )$ 关于y和 $\gamma$ 连续，则有

$\underset{j\to +\infty }{\lim \sup }{L}_{\beta }\left(x^{k_j+1},y^{k_j},{\gamma }^{k_j}\right)=\underset{j\to +\infty }{\lim \sup }{L}_{\beta }\left(x^{k_j+1},y^{k_j+1},{\gamma }^{k_j+1}\right)\le L_{\beta }\left(x^{*},y^{*},{\gamma }^{*}\right).$ (3.21)

由引理3.2，从而

$\left\{\left(x^{k_j+1},y^{k_j+1},{\gamma }^{k_j+1}\right)\right\}\to \left(x^{*},y^{*},{\gamma }^{*}\right),k_j\to +\infty$，由函数 $L_{\beta }(\cdot )$ 的下半连续性，可得

$\underset{j\to +\infty }{\lim \inf }{L}_{\beta }\left(x^{k_j+1},y^{k_j+1},{\gamma }^{k_j+1}\right)\ge L_{\beta }\left(x^{*},y^{*},{\gamma }^{*}\right).$ (3.22)

结合(3.21)式和(3.22)式，有 $\underset{j\to +\infty }{\lim }{L}_{\beta }\left(x^{k_j+1},y^{k_j+1},{\gamma }^{k_j+1}\right)=L_{\beta }\left(x^{*},y^{*},{\gamma }^{*}\right)$。

因此 $\underset{j\to +\infty }{\lim }f\left(x^{k_j+1}\right)=f\left(x^{*}\right)$。结合 $\nabla g,\nabla H_x\left(\cdot ,\cdot \right),\nabla H_y\left(\cdot ,\cdot \right)$ 的连续性，在式(3.2)中对序列 $\left\{\left(x^{k_j},y^{k_j},{\gamma }^{k_j}\right)\right\}$ 取极限，可得

$\{\begin{array}{l}{A}^{{\rm T}}{\lambda }^k-{\nabla }_{x}H\left(x^{k+1},y^k\right)\in \partial f\left(x^{*}\right),\\ {\lambda }^{k+1}-{\nabla }_{y}H\left(x^{k+1},y^{k+1}\right)=\nabla g\left(y^{*}\right),\\ A{x}^{*}+y^{*}-b=0.\end{array}$

因此 $\left(x^{*},y^{*},{\gamma }^{*}\right)\in S\left({\omega }^0\right)$。

iii) 对于任意点 $\left(x^{*},y^{*},{\gamma }^{*}\right)\in S\left({\omega }^0\right)$，存在子列 $\left\{\left(x^{k_j},y^{k_j},{\gamma }^{k_j}\right)\right\}\to \left(x^{*},y^{*},{\gamma }^{*}\right),k_j\to +\infty$，由于 $L_{\beta }\left({\omega }^k\right)$ 单调递减，有 $\underset{j\to +\infty }{\lim }{L}_{\beta }\left(x^k,y^k,{\gamma }^k\right)=L_{\beta }\left(x^{*},y^{*},{\gamma }^{*}\right)$。且 $L_{\beta }(\cdot )$ 在 $S\left({\omega }^0\right)$ 是常量。得证。

定理3.1若 $L_{\beta }(\cdot )$ 满足KL性质，则 ${\displaystyle \underset{k=0}{\overset{+\infty }{\sum }}{\Vert {\omega }^{k+1}-{\omega }^k\Vert }^2<+\infty }$，且序列 ${\left\{{\omega }^k\right\}}_{k\in N}$ 收敛到 $L_{\beta }(\cdot )$ 的一个稳定点。

证明由引理3.4可知， $\underset{k\to +\infty }{\lim }{L}_{\beta }\left({\omega }^k\right)=L_{\beta }\left({\omega }^{*}\right),\forall {\omega }^{*}\in S\left({\omega }^0\right)$，因此考虑以下两种情况。

i) 存在整数 $k_0$ 使得 $L_{\beta }\left({\omega }^{k_0}\right)=L_{\beta }\left({\omega }^{*}\right)$，由引理3.1可知

$\delta {\Vert v^{k+1}-v^k\Vert }^2-\frac{1}{2}{\Vert x-x^k\Vert }_G^2\le L_{\beta }\left({\omega }^k\right)-L_{\beta }\left({\omega }^{k+1}\right)\le L_{\beta }\left({\omega }^{k_0}\right)-L_{\beta }\left({\omega }^{*}\right)=0.$

因此对任意的 $k>k_0$，有 $v^{k+1}=v^k$，结合式(3.16)可知，对于任意的 $k>k_0+1$，有 ${\omega }^{k+1}={\omega }^k$ 成立，结论成立。

ii) 假设对于任意的k都有 $L_{\beta }\left({\omega }^k\right)>L_{\beta }\left({\omega }^{*}\right)$ 成立，存在 $\tilde{k}>0$ 使得对于所有的 $k>\tilde{k}$ 有

$\delta {\Vert v^{k+1}-v^k\Vert }^2\le \xi \cdot \Vert v^k-v^{k-1}\Vert \cdot {\Delta }_{k,k+1}.$ (3.23)

其中 ${\Delta }_{p,q}=\phi \left(L_{\beta }\left({\omega }^p\right)-L_{\beta }\left({\omega }^{*}\right)\right)-\phi \left(L_{\beta }\left({\omega }^q\right)-L_{\beta }\left({\omega }^{*}\right)\right)$。

由于 $d\left({\omega }^k,S\left({\omega }^0\right)\right)\to 0$ 且 $L_{\beta }\left({\omega }^k\right)\to L_{\beta }\left({\omega }^{*}\right)$，那么对于任意的 $\epsilon ,\kappa >0$，存在 $\tilde{k}>0$ 使得对于所有的 $k>\tilde{k}$ 有 $d\left({\omega }^k,S\left({\omega }^0\right)\right)<\epsilon ,L_{\beta }\left({\omega }^{*}\right)<L_{\beta }\left({\omega }^k\right)<L_{\beta }\left({\omega }^{*}\right)+\kappa .$

由于 $S\left({\omega }^0\right)$ 是非空紧集，且 $L_{\beta }(\cdot )$ 在 $S\left({\omega }^0\right)$ 是常数，由引理3.3可得对所有的 $k>\tilde{k}$ 有

${\phi }^{\prime }\left(L_{\beta }\left({\omega }^k\right)-L_{\beta }\left({\omega }^{*}\right)\right)d\left(0,\partial L_{\beta }\left({\omega }^k\right)\right)\ge 1.$

由于 $L_{\beta }\left({\omega }^k\right)-L_{\beta }\left({\omega }^{k+1}\right)=\left(L_{\beta }\left({\omega }^k\right)-L_{\beta }\left({\omega }^{*}\right)\right)-\left(L_{\beta }\left({\omega }^{k+1}\right)-L_{\beta }\left({\omega }^{*}\right)\right)$，

利用函数 $\phi$ 的凹性，可以得到

$\phi \left(L_{\beta }\left({\omega }^k\right)-L_{\beta }\left({\omega }^{\text{*}}\right)\right)-\phi \left(L_{\beta }\left({\omega }^{k+1}\right)-L_{\beta }\left({\omega }^{\text{*}}\right)\right)\ge {\phi }^{\prime }\left(L_{\beta }\left({\omega }^k\right)-L_{\beta }\left({\omega }^{\text{*}}\right)\right)\left(L_{\beta }\left({\omega }^k\right)-L_{\beta }\left({\omega }^{k+1}\right)\right).$

因此结合引理3.3以及 ${\phi }^{\prime }\left(L_{\beta }\left({\omega }^k\right)-L_{\beta }\left({\omega }^{\text{*}}\right)\right)>0$，可得

$\begin{array}{c}{L}_{\beta }\left({\omega }^k\right)-L_{\beta }\left({\omega }^{k+1}\right)\le \frac{\phi \left(L_{\beta }\left({\omega }^k\right)-L_{\beta }\left({\omega }^{\text{*}}\right)\right)-\phi \left(L_{\beta }\left({\omega }^{k+1}\right)-L_{\beta }\left({\omega }^{\text{*}}\right)\right)}{{\phi }^{\prime }\left(L_{\beta }\left({\omega }^k\right)-L_{\beta }\left({\omega }^{\text{*}}\right)\right)}\\ \le \xi \Vert v^k-v^{k-1}\Vert \Vert \phi \left(L_{\beta }\left({\omega }^k\right)-L_{\beta }\left({\omega }^{\text{*}}\right)\right)-\phi \left(L_{\beta }\left({\omega }^{k+1}\right)-L_{\beta }\left({\omega }^{\text{*}}\right)\right)\Vert \\ =\xi \Vert v^k-v^{k-1}\Vert {\Delta }_{k.k+1}.\end{array}$

结合引理3.2可得式(3.23)成立，且由(3.23)可得

$\Vert v^{k+1}-v^k\Vert \le \sqrt{\frac{\xi }{\delta }{\Delta }_{k,k+1}}\cdot {\Vert v^k-v^{k-1}\Vert }^{\frac{1}{2}}.$

利用不等式 $2\sqrt{\alpha \beta }\le \alpha +\beta \left(\forall \alpha ,\beta >0\right)$，可得

$2\Vert v^{k+1}-v^k\Vert \le \Vert v^k-v^{k-1}\Vert +\frac{\xi }{\delta }{\Delta }_{k,k+1}.$

进一步，将上式由 $k=\tilde{k}+1,\cdots ,m$ 相加得到

$2{\displaystyle \underset{k=\tilde{k}+1}{\overset{m}{\sum }}\Vert v^{k+1}-v^k\Vert \le {\displaystyle \underset{k=\tilde{k}+1}{\overset{m}{\sum }}\Vert v^k-v^{k-1}\Vert +\frac{\xi }{\delta }{\Delta }_{\tilde{k}+1,m}}}.$

由于 $\phi \left(L_{\beta }\left({\omega }^{m+1}\right)-L_{\beta }\left({\omega }^{\text{*}}\right)\right)>0$，令 $m\to +\infty$，上式为

${\displaystyle \underset{k=\tilde{k}+1}{\overset{+\infty }{\sum }}\Vert v^{k+1}-v^k\Vert }\le \Vert v^k-v^{k-1}\Vert +\frac{\xi }{\delta }\phi \left(L_{\beta }\left({\omega }^{\tilde{k}+1}\right)-L_{\beta }\left({\omega }^{\text{*}}\right)\right).$

也就是说 ${\displaystyle \underset{k=0}{\overset{+\infty }{\sum }}\Vert v^{k+1}-v^k\Vert }<+\infty$，因此 ${\displaystyle \underset{k=0}{\overset{+\infty }{\sum }}\Vert x^{k+1}-x^k\Vert }<+\infty ,{\displaystyle \underset{k=0}{\overset{+\infty }{\sum }}\Vert y^{k+1}-y^k\Vert }<+\infty$。

进一步由(3.12)可得 ${\displaystyle \underset{k=0}{\overset{+\infty }{\sum }}\Vert {\lambda }^{k+1}-{\lambda }^k\Vert }<+\infty$。

此外，由于

$\Vert {\omega }^{k+1}-{\omega }^k\Vert ={\left({\Vert x^{k+1}-x^k\Vert }^2+{\Vert y^{k+1}-y^k\Vert }^2+{\Vert {\lambda }^{k+1}-{\lambda }^k\Vert }^2\right)}^{\frac{1}{2}}\le \Vert x^{k+1}-x^k\Vert +\Vert y^{k+1}-y^k\Vert +\Vert {\lambda }^{k+1}-{\lambda }^k\Vert .$

因此 ${\displaystyle \underset{k=0}{\overset{+\infty }{\sum }}\Vert {\omega }^{k+1}-{\omega }^k\Vert }<+\infty$。且 ${\left\{{\omega }^k\right\}}_{k\in N}$ 是Cauchy序列，因此 ${\left\{{\omega }^k\right\}}_{k\in N}$ 收敛。

4. 数值实验

本节通过数值实验来验证算法的有效性。

考虑Lasso回归模型，即

$\min {\Vert Ax-b\Vert }^2+\gamma {\Vert x\Vert }_1,$ (4.1)

其中 ${\Vert x\Vert }_1={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|x_i\right|}$， $A\in R^{m\times n}$ 是设计矩阵， $\gamma >0$ 是正则化参数。

引进新变量y，则(4.1)式可转化为

$\begin{array}{l}\min {\Vert y\Vert }^2+\gamma {\Vert x\Vert }_1\\ \text{s}\text{.t}\text{.}Ax-y=b\end{array}$ (4.2)

为了验证本文算法RADMM的有效性，将算法(1.4)应用到问题(4.2)，且取定 $G=\alpha I-\beta A^{{\rm T}}A$，有

$\{\begin{array}{l}{x}^{k+1}\in S_{\gamma /\alpha }\left(x^k-\frac{\beta }{\alpha }{A}^{{\rm T}}A{x}^k+\frac{1}{\alpha }{A}^{{\rm T}}\left(\beta y^k+{\lambda }^k\right)\right),\\ y^{k+1}\in \frac{1}{2+\beta }\left(\beta A{x}^{k+1}-{\lambda }^k\right),\\ {\lambda }^{k+1}={\lambda }^k-\beta \left(A{x}^{k+1}-y^{k+1}\right),\end{array}$

其中S为软阈值算子，定义为

$S_{\kappa }\left(\alpha \right)=\{\begin{array}{l}\alpha -\kappa \alpha >\kappa \\ 0\left|\alpha \le -\kappa \right|\\ \alpha +\kappa \alpha <-\kappa \end{array}$

在实验中，定义终止准则为 ${\Vert A{x}^{k+1}-y^{k+1}\Vert }_2\le {ϵ}^{pri},{\Vert \beta A\left(y^{k+1}-y^k\right)\Vert }_2\le {ϵ}^{dual}$

其中， ${ϵ}^{pri}=\sqrt{n}{ϵ}^{abs}+{ϵ}^{rel}\max \left\{{\Vert A{x}^{k+1}\Vert }_2,{\Vert y^{k+1}\Vert }_2\right\},{ϵ}^{dual}=\sqrt{n}{ϵ}^{abs}+{ϵ}^{rel}{\Vert A{y}^{k+1}\Vert }_2$

设置 ${ϵ}^{pri}$ 和 ${ϵ}^{dual}$ 分别取10⁻⁴和10⁻²，设矩阵 $A\in R^{m\times n}$ 随机生成且服从标准正态分布 $N\left(0,1\right)$，实验选取了矩阵A从900 × 3000到1500 × 5000的五个维度的情形，取正则化参数 $\gamma =0.1,\beta =1,\alpha =0.3$。

得到的实验结果如图所示。

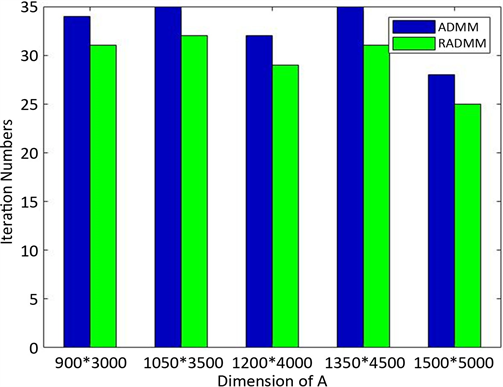
Figure 1. Comparison of ADMM algorithm and RADMM algorithm for Lasso model

图1. 对于Lasso模型ADMM算法和RADMM算法的比较

根据图1我们可以看到，当矩阵A取不同维度时，本文提出的算法RADMM以及原始ADMM算法在求解Lasso模型的平均迭代次数，可以看出算法(1.4)的性能明显优于原始的ADMM算法。

5. 结论

本文针对一类非凸不可分离的问题提出了正则化交替方向乘子法，证明了算法的全局收敛性。并且在增广拉格朗日函数满足KL性质的条件下，证明了算法的强收敛性。最后，将算法应用于Lasso模型求解，证明了算法的有效性。