基于AIC, BIC, CV准则的模型选择

Model Selection Based on AIC, BIC, CV Criteria

摘要: 众所周知，一个好的模型不仅要具有优良的拟合度，而且还要具有简洁的形式，那么究竟怎样平衡模型的精确度与复杂度呢，这就需要进行模型选择了。而AIC, BIC及CV恰好能平衡模型这种关系，恰好解决了当下模型选择的难题。本文依据AIC, BIC及CV准则来进行模型选择，对WAGE2数据进行建模。首先对12个变量通过简单统计量及其统计作图得到数据的一些分布特征及其相关关系。接着用AIC, BIC及CV来进行统计建模，选出最优模型，并用最小二乘法求得拟合方程，然后进行经济学意义的解释。最后为了让模型的选择更具有说服力，重复1000次实验选出最优模型，与之前的模型进行比较，得到一致最优的模型。

Abstract: As we all know, a good model must not only have a good fit, but also have a concise form, so how to balance the accuracy and complexity of the model requires model selection. And AIC, BIC and CV can just balance the relationship of the model, which just solves the problem of current model selection. This article chooses models based on AIC, BIC and CV criteria, and models WAGE2 data. Firstly, some distribution characteristics and correlations of the data are obtained through simple statistics and statistical mapping for the 12 variables. Then, we use AIC, BIC and CV to conduct statistical modeling, select the optimal model, and use least squares method to find the fitting equation, and then explain the economic significance. Finally, in order to make the selection of the model more convincing, the optimal model was selected by repeating 1000 experiments, and compared with the previous model to obtain a consistent optimal model.

1. 绪论

1.1. 研究背景及意义

随着社会科学的发展，模型选择是很多研究学者讨论的一个重要话题，究竟应该怎样评判一个模型的好坏呢，它的拟合优度及其参数选择怎样才更合理呢，这是一个值得研究与探索的问题。

模型选择一定伴随着参数估计的问题，有很多学者采用极大似然函数作为目标函数，这也是评判拟合优度的一个标准。为了提高模型的精度，我们可以选用较多的训练样本，但是，一般情况下，模型精度的提高伴随着另一个问题就是模型的复杂度变大了，为此，就可能出现另外一种结果，出现过度拟合的情况，因此，对于模型的选择是一个迫切需要研究的课题，要怎样在模型的精确度与复杂度之间平衡呢？AIC, BIC [1] 及其CV [3] 在这方面就很好的平衡了这两者之间的关系，而本文就依托这三个模型选择的准则来选择最优模型。

1.2. 文献综述

关于模型识别国内外有很多学者做了相关研究，特别是关于AIC, BIC准则的模型识别。

YUHONG YANG [1] 在AIC和BIC的优势可以共享吗？模型辨识与回归估计的关系这篇文章中提出在模型选择中，BIC在选择真模型时是一致的，AIC在估计回归函数时是最优的极大极小率。最近的一个发展方向是自适应模型选择，与AIC和BIC相比，惩罚项是数据相关的。在自适应模型选择的支持下，已经取得了一些理论和实证结果，但目前还不清楚它是否能真正共享AIC和BIC模型的结合或平均的强度，已引起越来越多的关注，这是克服模型选择不确定性的一种方法，贝叶斯模型平均值是否是估计模型的最佳方法？最小极大意义上的回归函数？我们发现，这些问题的答案基本上是否定的：对于任何一个模型选择准则都是一致的，它必须表现出次优的行为来估计覆盖率极小极大值项下的回归函数；而贝叶斯模型平均不能成为回归估计的极小极大值。Cheryl J. Flynn [2] 在规范化参数选择的效率——误判模式的惩罚似然估计这篇文章中提出，在经典回归中，当最大候选模型的维数与样本量之间存在较大的相关性时，AIC往往会选择过于复杂的模型，仿真研究表明，AIC在使用惩罚回归时，会有一些缺点。因此，提出了使用经典校正AIC(AICC)作为替代方案，并证明它保持了所需的渐近性质。Jun Shao [3] 在交叉验证发的线性模型的选择这篇文章中提出可以通过使用遗漏n交叉验证，可以纠正遗漏1交叉验证的一致性，并且给出了使用遗漏交叉验证方法的动机、理由和一些实用性的讨论，并给出了仿真研究的结果。

1.3. 研究问题概述

本文主要的研究问题有5个：

1)：对给出的12个变量进行描述性的统计分析；

2)：依托全部数据用AIC, BIC, CV准则从12个模型中选出最优模型；

3)：对最优模型用最小二乘法进行拟合，求得参数，获得模型的方程。

4)：对所获得的最优方程进行经济学意义的解释。

5)：重复进行1000次实验，把数据分为训练集与测试集，用AIC, BIC, CV来进行模型选择，选出最优模型。

1.4. 研究思路和行文框架

本文的研究思路是先对对数据进行描述性统计分析，然后再利用AIC, BIC及CV准则来进行模型选择。

本文具体的行文安排如下：第一章绪论部分，从模型选择的研究意义出发说明研究本文的必要性，然后分析了模型选择的研究现状，并给出本文的研究思路及行文框架。第二章主要是相关知识准备，主要包括AIC, BIC及CV的简介原理及其实现步骤。第三章是对数据进行描述性的统计分析。第四章主要依托第二章的相关知识用AIC, BIC及CV这三个准则进行模型选择。先用这三个准则进行模型选择，接着再用最小二乘法对最优模型进行拟合，求得参数，获得最优方程，并且对最优方程进行经济学解释。最后，为了让结果更具有说服力，重复进行1000次实验，来选出最优模型。第五章为研究结论，主要是针对本文所做的分析做一个总结。

2. 相关知识准备

2.1. AIC, BIC, CV的简介与原理

1) AIC的简介及原理

AIC是赤池信息准则的简称，是日本的一个统计学家赤池宏次提出的，它的用途是衡量统计模型拟合度是否优良，对多个模型做出选择判别。不仅如此，它在估计模型的复杂度方面也有很大的用途。AIC准则主要在熵的基础上建立的，一般情况下，认为AIC越小，所对应的模型拟合度越好，模型越精确。 [4]

AIC的一般表达式为：

$\text{AIC}=\left(2k-2L\right)/n$ (1)

k表示的是模型中参数的个数，L表示的是对数似然函数，n是样本量。

我们要想选取AIC最小的那个模型，需要做到两点：

一是要提高极大似然函数的拟合度，即提高模型的拟合度。

二是：要降低过度拟合的可能性，这就需要加入惩罚项，使模型的参数尽可能少。

显然，AIC准则在合理控制了参数的同时也使得似然函数尽可能大，模型的拟合度尽可能高。

特别注意的是AIC的使用条件一定是在误差项服从正太分布的情况下。

2) BIC的简介及原理

BIC是贝叶斯信息准则的简称，是Schwarz提出的，它与AIC准则相似，也是用于模型选择。当增加参数k的数量时，就增加了模型的复杂度，似然函数也会增大，与AIC相似，也易导致过度拟合的现象。针对此现象，AIC, BIC的处理方式相似，都引入了与参数相关的惩罚项，但是BIC的惩罚项会更大一点相对AIC而言，因此，考虑了样本量，样本量较大时，就有效的解决了由于模型精度过高导致的复杂度也较高的问题。

BIC的一般表达式为：

$\text{BIC}=k\ln \left(n\right)-2\ln \left(L\right)$ (2)

k表示的是模型中参数的个数，L表示的是对数似然函数，n是样本量， $k\ln \left(n\right)$ 表示惩罚项。

3) CV的简介及原理

CV是交叉验证法的简称，它也是一种分类的统计分析方法，它的基本思想是对原始的数据集分组为两部分，训练集与验证集。先对训练集进行训练，然后再用验证集对训练的模型进行测试，进一步进行分类评价。

最常见的CV方法主要有2种：

a) 一种是将原始数据进行分组，将其中的一组数据作为验证，其余的K-1组作为训练集，这样就可以得到k个模型，一般情况k大于2，分类结果还是相对有效的。

b) 另外一种方法与第一种方法的不同是将每个样本都做一次验证集，剩下的全部样本作为训练集，假设有n个样本，则共有n个模型。最终可以取分类准确率的平均数来作为分类的性能指标。几乎用上了所有样本作为训练集，最接近原始的样本，几乎没有信息损失，结果更为可靠，这种方法更受欢迎。

本文的CV方法采用的就是第二种方法。

2.2. AIC, BIC, CV的实现步骤

1) AIC, BIC模型的实现步骤

a) 计算总体的概率密度。假设 $y_i,i=1,\cdots ,n$，是来自总体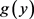的样本。

$y_i=X_i\beta +{\epsilon }_i$ (3)

其中 ${{\displaystyle y}}_i~N\left({X^{\prime }}_i,{{\displaystyle \sigma }}^2\right)$， ${\epsilon }_i\stackrel{iid}{~}N\left(0,{\sigma }^2\right)$

若 $y_i$ 的密度函数为

$f\left(y_i|\beta ,{\sigma }^2\right)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(\frac{-{\left(y_i-{X^{\prime }}_i\beta \right)}^2}{2{\sigma }^2}\right)$ (4)

则似然函数为

$L=f\left(y|\beta ,{\sigma }^2\right)={\displaystyle \underset{1}{\overset{n}{\prod }}f\left(y_i|\beta ,{\sigma }^2\right)}={\displaystyle \underset{i=1}{\overset{n}{\prod }}\left\{\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(\frac{-{\left(y_i-{X^{\prime }}_i\beta \right)}^2}{2{\sigma }^2}\right)\right\}}$ (5)

b) 计算对数似然函数。对数似然函数为

$\ln L=-\frac{n}{2}\ln \left(2\pi \right)-\frac{n}{2}\ln \left({\sigma }^2\right)-\left\{\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-{X^{\prime }}_i\beta \right)}^2}}{2{\sigma }^2}\right\}$ (6)

c) 求出参数 $\sigma {}^2$ 的极大似然估计

${\hat{\sigma }}_2=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-{X^{\prime }}_i\beta \right)}^2}}{n}$ (7)

d) 计算 $\beta$ 的最小二乘估计

在正太分布的情况， $\beta$ 的极大似然估计与最小二乘估计无大的区别。在本文中用的是最小二乘估计。

$\hat{\beta }={\left(X^{\prime }X\right)}^{-1}{X}^{\prime }y$ (8)

e) 计算AIC与BIC。将计算得到的参数估计值代入计算AIC, BIC

$AIC=-2L\left(\hat{\beta },{\hat{\sigma }}^2|Y\right)+2\left(p+1\right)$ (9)

$BIC=-2L\left(\hat{\beta },{\hat{\sigma }}^2|Y\right)+\left(p+1\right)\ln \left(n\right)$ (10)

其中p表示的是参数的数目，n表示的是总的样本量。

2) CV模型的实现步骤

设总的数据的样本书目为n， $y_i$ 为因变量， $x_i$ 为自变量，用CV来选择模型。

第一步：删除 $\left(x_1,y_1\right)$，用 $\left(x_2,y_2\right),\cdots ,\left(x_n,y_n\right)$ 作为训练集，用最小二乘法来做参数估计。

${\hat{\beta }}_{\left[-1\right]}={\left(X^{\prime }X\right)}^{-1}{X}^{\prime }y$ (11)

其中 ${\hat{\beta }}_{\left[-1\right]}$ 表示已经去除了第一个样本的参数估计值。预测误差为 ${\left(y_1-{x^{\prime }}_1{\hat{\beta }}_{\left[-1\right]}\right)}^2$。

第二步：删除，用 $\left(x_1,y_1\right),\left(x_3,y_3\right),\cdots ,\left(x_n,y_n\right)$ 作为训练集，用最小二乘法来做参数估计。

${\hat{\beta }}_{\left[-2\right]}={\left(X^{\prime }X\right)}^{-1}{X}^{\prime }y$ (12)

其中 ${\hat{\beta }}_{\left[-2\right]}$ 表示已经去除了第二个样本的参数估计值。

预测误差为 ${\left(y_2-{x^{\prime }}_2{\hat{\beta }}_{\left[-2\right]}\right)}^2$。

第三步往后，依次删除一个样本，用这个删除的样本作为测试集，用剩下的样本来做参数估计，并求得预测误差。

最后一步：删除 $\left(x_n,y_n\right)$，用 $\left(x_1,y_1\right),\cdots ,\left(x_{n-1},y_{n-1}\right)$ 作为训练集，用最小二乘法来做参数估计。

${\hat{\beta }}_{\left[-n\right]}={\left(X^{\prime }X\right)}^{-1}{X}^{\prime }y$ (13)

其中 ${\hat{\beta }}_{\left[-2\right]}$ 表示已经去除了第二个样本的参数估计值。

预测误差为 ${\left(y_n-{x^{\prime }}_n{\hat{\beta }}_{\left[-n\right]}\right)}^2$

总共进行了n次，则有n个预测误差。

计算累加的误差之和。

$\text{CV}={\displaystyle \underset{1}{\overset{n}{\sum }}{\left(y_i-{x^{\prime }}_i{\hat{\beta }}_{\left[-i\right]}\right)}^2}$ (14)

则CV就是当前模型的误差。

如果有k个模型，只需要比较这k个CV值，选择最小CV值对应的模型就是最优的模型。

3. 对数据的描述性统计分析

3.1. 数据准备

本文的数据来源于WAGE2，共有935个样本，12个变量，本文主要对这12个变量进行数据分析，变量说明如下表1。

Table 1. Description of variables in wage2

表1. WAGE2中的变量说明

3.2. 统计特征

运用MATLAB来进行统计分析，运行代码，得到的统计结果如下表2~5，代码见附录1。

1) 平均值

Table 2. Average values of variables in wage2

表2. WAGE2中的变量的平均值

2) 中位数

Table 3. Median of variables in wage2

表3. WAGE2中的变量的中位数

3) 众数

Table 4. Modes of variables in wage2

表4. WAGE2中的变量的众数

4) 方差

Table 5. Variance of variables in wage2

表5. WAGE2中的变量的方差

通过(1) (2) (3) (4)平均数，中位数，众数，与方差的数据特征，我们可以发现，y，x4，x8，x9，x10，x11的数据方差比较小，说明数据分布是较为集中的，它们的中位数与众数都是几乎相同的，说明在中位数附近的数据是较为集中的。

5) 图1是12个变量的相关系数矩阵

Figure 1. Correlation coefficients of variables in wage2

图1. WAGE2中的变量的相关系数

由12个变量的相关系数图可以看出，对数工资y与变量x1，x9，x10成反比，与x2，x3，x4，x5，x6，x7，x8，x11成正比，其中与x2的相关性最大，其相关系数为0.3148，说明了对数工资与智商之间的相关性最强。

3.3. 统计作图

通过统计作图可以直观的发现数据特征，运用MATLAB画图，得到的统计结果如下，代码见附录2。

1) 12个变量的盒形图，见图2。

Figure 2. Box diagram of variables in wage2

图2. WAGE2中的变量的盒形图

上图盒形图更加直观的体现了数据的集中于分散程度，还提供了上四分位数，中位数，下四分位数的信息，能够跟家直观的反应统计特征信息。例如从上图可以观察到变量y与x8，x9，x10，x11的数据都是较为集中，并且还可以根据分位点，中位数来判断数据的分布情况。

2) 样本概率图形。

对y这个变量做概率图形，由前面的概率特征可知，平均值为6.779众数为6.9078。我们想要求得对数工资y在区间[6, 7.5]概率，如下图3结果。

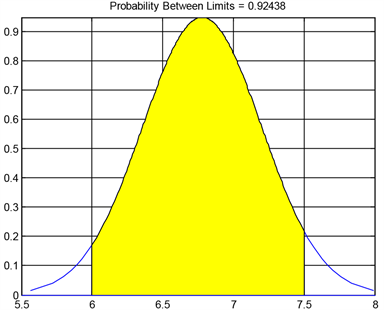
Figure 3. Sample probability graph of logarithmic wage

图3. 对数工资的样本概率图形

可以直观的发现对数工资y在区间[6, 7.5]概率是92.4%，这说明的大多数数据都集中在6到7.5这个区间，只有极小部分不在这个区间。也可以类似的去查看其他变量的数据分布所占比例。

4. AIC, BIC, CV模型选择与分析

4.1. 问题回顾

本章用线性模型研究“对数薪水”和其他协变量之间的关系，考虑12个带有嵌套结构的备选模型

模型1： $y_i={\beta }_0+{\epsilon }_i$， ${\epsilon }_i\stackrel{iid}{~}N\left(0,{\sigma }^2\right)$

模型2： $y_i={\beta }_0+{\beta }_1{x}_i+{\epsilon }_i$，

………

模型12： $y_i={\beta }_0+{\beta }_1{x}_i+\cdots +{\beta }_{11}{x}_{11}{\epsilon }_i$， ${\epsilon }_i\stackrel{iid}{~}N\left(0,{\sigma }^2\right)$

旨在用AIC, BIC, CV来从这12个模型中选择合适的模型，更好的解释对数薪水与其他协变量之间的关系，其中的变量说明见表1。

4.2. 对WAGE2中的全部数据来进行模型选择

1) 本节目的：依托WAGE2中所有的935个数据，使用CV，AIC和BIC，从上述12个备选模型里选择合适的模型。

2) 根据2.2节AIC, BIC模型的实现步骤先对全部数据进行模型选择，运行MATLAB代码，见附录3，可以得到AIC, BIC选择模型的结果。

结果如下表6。

Table 6. AIC values of 12 models

表6. 12个模型的AIC值

其中最小的AIC的值为759.2700765，对应的模型为12，故有AIC准则确定最优的模型应该为第12个。

Table 7. BIC values of 12 models

表7. 12个模型的BIC值

由表7知，其中最小的BIC的值为822.1971814，对应的模型为12，故由BIC准则确定最优的模型也是第12个。

3) 用CV来对全部数据处理，选出最优的模型。

用935个数据，每次抽出一行作为验证集，剩下的934个样本作为训练集，总共需要进行935次，运行MATLAB代码得到如下次结果，代码见附录4。

将CV记作12个模型935次预测误差求和，则最小的CV值就对应最优的模型。

Table 8. CV values of 12 models

表8. 12个模型的CV值

由上表8的结果知，最小的CV值为123,2714065，对应的模型为第12个，故由CV的判别准则第12个模型是最优的。

综上：AIC, BIC, CV这三个判别准则所选的模型都是第12个模型，所以第12个模型就是最优模型。

4) 用最小二乘法对第12个模型进行拟合，运行MATLAB代码，见附录5，加结果如下：

第12个模型中y与x的散点图如下图4。

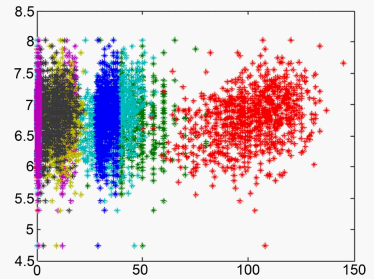
Figure 4. Scatter plot of the 12th model

图4. 第12个模型的散点图

最小二乘估计的参数结果如下表9。

Table 9. CV values of 12 models

表9. 12个模型的CV值

第12个模型拟合的方程如下

$\begin{array}{c}y=5.2797-0.006x_1+0.0033x_2+0.0035x_3+0.0492x_4+0.0105x_5+0.01x_6\\ +0.0054x_7+0.195x_8-0.142x_9-0.081x_{10}+0.1775x_{11}\end{array}$

4.3. 经济学原理对4.2的结果进行解释

由4.2的结果知，AIC, BIC与CV所选的模型都为第12个模型，且由最小二乘估计得到了第12个模型的拟合的方程

$\begin{array}{c}y=5.2797-0.006x_1+0.0033x_2+0.0035x_3+0.0492x_4+0.0105x_5+0.01x_6\\ +0.0054x_7+0.195x_8-0.142x_9-0.081x_{10}+0.1775x_{11}\end{array}$

我们发现，

1) y与变量x1的系数为负值，说明lwage与hours是成反比的关系，hours每减少1个单位，lwage增加0.006个单位，说明了现代社会对效率的要求越来越高，效率越高，报酬越多；

2) y与变量x2的系数为正值，说明lwage与IQ是成正比关系，说明智商每增加一个单位，对数工资就增加0.0033个单位，同时也说明了智商高的人获得的工资报酬就越高；

3) y与变量x3的系数为正值，说明lwage与kww是成正比关系，说明世界工作知识得分每增加一个单位，对数工资就增加0.0035个单位；

4) y与变量x4的系数为正值，说明lwage与educ是成正比关系，说明教育每增加一个单位，对数工资就增加0.0492个单位；

5) y与变量x5的系数为正值，说明lwage与exper是成正比关系，说明工作经验每增加一个单位，对数工资就增加0.0105个单位。

6) y与变量x6的系数为正值，说明lwage与enure是成正比关系，说明与现任雇主共事年限每增加一个单位，对数工资就增加0.01个单位。

7) y与变量x7的系数为正值，说明lwage与age是成正比关系，说明在一定的年龄范围内，年龄每增加一个单位，对数工资就增加0.0054个单位。因为在一定年龄范围内，年龄大的人相对来讲工作经验会多一点，知识储备会多一些，所以获得的工资报酬也会相对的高一些。

8) y与变量x8的系数为正值，说明lwage与married是成正比关系，说明已婚每增加一个单位，对数工资就增加0.195个单位。

9) y与变量x9的系数为负值，说明lwage与black是成反比关系，说明黑人获得的工资会更少一些，同时也说明了现代社会依然存在着种族歧视。

10) y与变量x10的系数为负值，说明lwage与south是成反比关系，说明越靠近南边，工资越少，因为当前全球区域经济发展不平衡，例如南非，经济发展落后，所以工资报酬会更低一点。

11) y与变量x11的系数为正值，说明lwage与urban是成正比关系，说明了生活在标准城市统计区的人工资报酬会更高一点。因为标准城市区域经济会相对发达一点，所以工资报酬会相对较高一点。

4.4. 将WAGE2的数据分为训练集与测试集，重新进行模型选择

在4.2节中，我们只对模型进行了一次选择，并不很具有说服力，所以在本小节，我们对模型重复进行1000次选择，采用随机抽样的方法将数据集随机地分为训练集(500个样本)和测试集(435个样本)，依托训练集，使用CV，AIC和BIC，从12个备选模型里选择模型，并用选出的模型预测测试集里的测试样本，考察预测误差评价CV，AIC和BIC三种模型选择准则中哪种准则的表现最好。

运行MATLAB代码，得到结果，代码见附录6。

1) 图5是12个模型与运行1000次得到的AIC，维度为12行1000列。由于空间有限，仅显示部分结果。

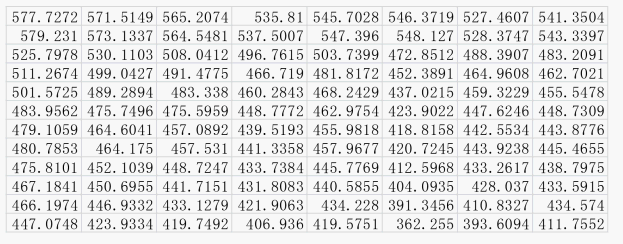
Figure 5. AIC values from 1000 runs

图5. 运行1000次得到的AIC值

可以发现，1000次运行结果中都是第12个模型的AIC的值最小，故选择第12个模型为最优模型。

下图是最小AIC对应模型的预测误差(即第12个模型的预测误差)，因为重复进行1000次，故有1000个预测误差，空间有限仅显示前10次的结果，见表10。

Table 10. Prediction error of corresponding model for minimum AIC

表10. 最小AIC对应模型的预测误差

2) 下图是12个模型与运行1000次得到的BIC，也仅展示部分结果，见图6。

Figure 6. BIC values from 1000 runs

图6. 运行1000次得到的BIC值

同样可以发现，1000次运行结果中都是第12个模型的BIC的值最小，故选择第12个模型为最优模型。

下图是最小BIC对应模型的预测误差(即第12个模型的预测误差)，因为重复进行1000次，故有1000个预测误差，空间有限仅显示前10次的结果，见表11。

Table 11. Prediction error of minimum BIC corresponding model

表11. 最小BIC对应模型的预测误差

3) 下图是CV运行1000次得到的预测误差，共12行1000列，篇幅限制，仅展示部分结果，见图7。

Figure 7. Prediction error for 1000 runs of CV

图7. 运行1000次CV的预测误差

下图是1000次中每次选中的模型，篇幅限制，仅展示部分结果，见表12。

Table 12. Optimal model for each selection in 1000 times

表12. 1000次中每次选中的最优模型

下图是1000次中每个模型被选中的概率。

Table 13. Proportion of each model selected in 1000 times

表13. 1000次中每个模型被选中的比例

由表13，可以发现第12个模型被选中的比例最高，为22.8%，其他模型被选中的比例明显都比较小，所以CV模型选中的依然是第12个模型。

综上：AIC, BIC, CV三个模型选出的全部为第12个模型最优，故认为第12个模型为最优的模型。

5. 研究结论

依托前面的知识准备，通过第三章的描述性统计分析，可以清楚直观的看到数据的分布特征及其变量的相关关系。然后在第四章用AIC, BIC, CV准则依托全部数据来进行模型选择，最后3个准则选出的最优模型均为第12个模型，故此，对第12个模型用最小二乘法进行了拟合，求得参数，得到方程，进而用经济学原理对求得的第12个模型进行解释。但是考虑到一次实验结果并不是十分具有说服力，因此，又将实验重复1000次，再次看模型选择的结果，结果发现AIC, BIC在这1000次实验中一致选择的是第12个模型，而CV选择的模型依概率算是占比最高的，为22.8%，说明在1000次实验中，选择第12个模型的次数占228次。而选择其他模型的比例最高占据11.4%，故此一致认为第12个模型是最优的。

附录

附录1：统计特征

load('C:\Users\Administrator\Desktop\wage2.mat')

n = length(y); Data = [y,x];

M1 = mean(Data); M2 = median(Data); M3 = mode(Data);

V = var(Data); C = cov(Data); Corr = corrcoef(Data);

附录2：统计作图

%绘制盒形图

subplot(3,1,1); boxplot(Data);subplot(3,1,2);

boxplot(Data,' plotstyle','compact');

subplot(3,1,3); boxplot(x,'notch','on');

%绘制对数工资的样本概率图形

p1 = capaplot(y,[6 7.5]); grid on; axis tight;

p2 = capaplot(y,[6.9 8.8]); grid on; axis tight;

附录3：AIC, BIC依托全数据进行模型选择

%AIC, BIC做模型选择

%用全部的数据935个数据进行AIC, BIC模型选择

%[AIC,BIC,c2AIC,c2BIC] = Fun1AB(x,y)

%y表示的是lwage

%x表示的是hours,IQ,KWW,educ,exper,tenure,age,married,black,south,urban这11个变量

function [AIC,BIC,c2AIC,c2BIC] = Fun1AB(x,y)

%_________________( AIC,BIC数据准备 )__________________________________

n = length(y); Data = [y,ones(n,1),x];

X= Data(:,2:13);

X1= X(:,1);X2 = X(:,1:2); X3= X(:,1:3); X4= X(:,1:4); X5= X(:,1:5); X6 = X(:,1:6); X7= X(:,1:7);

X8= X(:,1:8); X9= X(:,1:9);X10= X(:,1:10); X11= X(:,1:11); X12= X(:,1:12);

%___________________模型1的AIC与BIC构建-----------------------------------

hb1 = [(X1'*X1)\(X1'*y);zeros(11,1)];%第一个模型的参数beta，为了保证与后面11个模型的参数维度一致，所以补11行1列的0

hsig21 = mean((y − X*hb1).^2);%模型1的sig2的极大似然估计

L1 = −n*log(2*pi)/2 − n*log(hsig21)/2 − n/2;%模型1的极大似然函数

AIC1 = −2*L1 + 2*2; %模型1的赤池信息准则，存储在AIC的第1行第k列

BIC1 = −2*L1 + log(n)*2; %模型1的贝叶斯信息准则，存储在BIC的第1行第k列

%__________________模型2的AIC与BIC构建 ______________________________

hb2 = [(X2'*X2)\(X2'*y);zeros(10,1)];%第二个模型的参数beta,为了保证与beta3的参数维度一致，所以补10行1列的0

hsig22 = mean((y − X*hb2).^2);%模型2的sig2的极大似然估计

L2 = −n*log(2*pi)/2 − n*log(hsig22)/2 − n/2;%模型2的极大似然函数

AIC2 = −2*L2 + 2*3; %模型2的赤赤池信息准则，存储在AIC的第2行第k列

BIC2 = −2*L2 + log(n)*3;%模型2的贝叶斯信息准则,存储在BIC的第2行第k列

%_________________ 模型3的AIC与BIC构建 ________________________________

hb3 = [(X3'*X3)\(X3'*y);zeros(9,1)];%第三个模型的参数beta

hsig23 = mean((y − X*hb3).^2);%模型3的sig2的极大似然估计

L3 = −n*log(2*pi)/2 − n*log(hsig23)/2 - n/2;%模型3的极大似然函数

AIC3 = −2*L3 + 2*4; %模型3的赤池信息准则,存储在AIC的第3行第k列

BIC3 = −2*L3 + log(n)*4;%模型3的贝叶斯信息准则，存储在BIC的第3行第k列

%_________________ 模型4的AIC与BIC构建 ________________________________

hb4= [(X4'*X4)\(X4'*y);zeros(8,1)]; hsig24 = mean((y − X*hb4).^2);

L4 = −n*log(2*pi)/2 − n*log(hsig24)/2 − n/2;

AIC4 = −2*L4 + 2*5; BIC4= -−2*L4 + log(n)*5;

%_________________模型5的AIC与BIC构建 ________________________________

hb5= [(X5'*X5)\(X5'*y);zeros(7,1)];hsig25 = mean((y - X*hb5).^2);

L5= −n*log(2*pi)/2 − n*log(hsig25)/2 −n/2;

AIC5 = −2*L5 + 2*6; BIC5 = −2*L5 + log(n)*6;

%_________________模型6的AIC与BIC构建 ________________________________

hb6 = [(X6'*X6)\(X6'*y);zeros(6,1)];hsig26 = mean((y − X*hb6).^2);

L6 = −n*log(2*pi)/2 − n*log(hsig26)/2 − n/2;

AIC6 = −2*L6 + 2*7;BIC6 = −2*L6 + log(n)*7;

%_________________模型7的AIC与BIC构建 ________________________________

hb7 = [(X7'*X7)\(X7'*y); zeros(5,1)]; hsig27 = mean((y − X*hb7).^2);

L7= −n*log(2*pi)/2 - n*log(hsig27)/2 - n/2;

AIC7= -2*L7+ 2*8;BIC7 = -2*L7 + log(n)*8;

%_________________ 模型8的AIC与BIC构建 ________________________________

hb8= [(X8'*X8)\(X8'*y);zeros(4,1)];hsig28 = mean((y - X*hb8).^2);

L8 = −n*log(2*pi)/2 − n*log(hsig28)/2 −n/2;

AIC8 = −2*L8+ 2*9; BIC8 = −2*L8 + log(n)*9;

%_________________ 模型9的AIC与BIC构建 ________________________________

hb9 = [(X9'*X9)\(X9'*y);zeros(3,1)];hsig29 = mean((y - X*hb9).^2);

L9 = −n*log(2*pi)/2 − n*log(hsig29)/2 − n/2;

AIC9 = −2*L9 + 2*10; BIC9 = −2*L9 + log(n)*10;

%_________________模型10的AIC与BIC构建 ________________________________

hb10 = [(X10'*X10)\(X10'*y); zeros(2,1)];hsig210 = mean((y − X*hb10).^2);

L10 = −n*log(2*pi)/2 − n*log(hsig210)/2 − n/2;

AIC10= -2*L10+ 2*11;BIC10 = -2*L10 + log(n)*11;

%_________________ 模型11的AIC与BIC构建 ________________________________

hb11 = [(X11'*X11)\(X11'*y);0];hsig211 = mean((y - X*hb11).^2);

L11 = −n*log(2*pi)/2 − n*log(hsig211)/2 − n/2;

AIC11 = −2*L11 + 2*12; BIC11 = −2*L11 + log(n)*12;

%_________________ 模型12的AIC与BIC构建 ________________________________

hb12 = [(X12'*X12)\(X12'*y)]; hsig212 = mean((y − X*hb12).^2);

L12 = −n*log(2*pi)/2 − n*log(hsig212)/2 − n/2;

AIC12 = −2*L12+ 2*13; BIC12 = −2*L12 + log(n)*13;

AIC = [AIC1,AIC2,AIC3,AIC4,AIC5,AIC6,AIC7,AIC8,AIC9,AIC10,AIC11,AIC12]

BIC = [BIC1,BIC2,BIC3,BIC4,BIC5,BIC6,BIC7,BIC8,BIC9,BIC10,BIC11,BIC12]

% _______________选出12个模型中的最小的AIC与BIC __________________________

附录4：用CV依托全数据进行模型选择

%=======================CV做模型选择======================================

%输入数据

%load('C:\Users\Administrator\Desktop\wage2.mat')

%[CV,c1CV,c2CV] = Fun1CV(x,y)

function [CV,c1CV,c2CV] = Fun1CV(x,y)

n = length(y);%总的样本量

Data = [y,ones(n,1),x];%构造的数据矩阵

for i = 1:n

%____________________ CV数据准备______________________________________

yTrain = Data(:,1);yTrain(i,:) = [];yTest = Data(i,1);

xTrain = Data(:,2:13);xTrain(i,:) = []; xTest = Data(i,2:13);

%_______________12个CV模型的变量数据____________________________________

X1 = xTrain(:,1); X2 = xTrain(:,1:2); X3 = xTrain(:,1:3); X4 = xTrain(:,1:4); X5 = xTrain(:,1:5);

X6 = xTrain(:,1:6); X7 = xTrain(:,1:7); X8 = xTrain(:,1:8); X9 =xTrain(:,1:9); X10 = xTrain(:,1:10);

X11 = xTrain(:,1:11);X12 = xTrain(:,1:12);

%______________________ 12个CV模型的预测误差_____________________________

pe1(i)=(yTest-xTest(:,1)*((X1'*X1)\(X1'*yTrain)))^2;

pe2(i)=(yTest-xTest(:,1:2)*((X2'*X2)\(X2'*yTrain)))^2;

pe3(i) = (yTest - xTest(:,1:3)*((X3'*X3)\(X3'*yTrain)))^2;

pe4(i) = (yTest - xTest(:,1:4)*((X4'*X4)\(X4'*yTrain)))^2;

pe5(i) = (yTest - xTest(:,1:5)*((X5'*X5)\(X5'*yTrain)))^2;

pe6(i) = (yTest - xTest(:,1:6)*((X6'*X6)\(X6'*yTrain)))^2;

pe7(i) = (yTest - xTest(:,1:7)*((X7'*X7)\(X7'*yTrain)))^2;

pe8(i) = (yTest - xTest(:,1:8)*((X8'*X8)\(X8'*yTrain)))^2;

pe9(i) = (yTest - xTest(:,1:9)*((X9'*X9)\(X9'*yTrain)))^2;

pe10(i) = (yTest - xTest(:,1:10)*((X10'*X10)\(X10'*yTrain)))^2;

pe11(i) = (yTest - xTest(:,1:11)*((X11'*X11)\(X11'*yTrain)))^2;

pe12(i) = (yTest - xTest(:,1:12)*((X12'*X12)\(X12'*yTrain)))^2;

end

%_______________CV预测误差求和____________________________

CV=[sum(pe1);sum(pe2);sum(pe3);sum(pe4);sum(pe5);sum(pe6);sum(pe7);sum(pe8);sum(pe9);sum(pe10);sum(pe11);sum(pe12)];

附录5：最小二乘法拟合第12个模型

%用最小二乘法对的12个模型做拟和

load('C:\Users\Administrator\Desktop\wage2.mat')

plot(X12,y,'*');n = length(y); X= Data(:,2:13);Data = [y,ones(n,1),x];

X12 = X(:,1:12);hb12= [(X12'*X12)\(X12'*y)];

附录6：重复1000次，用AIC,BIC,CV来进行模型选择

%=================AIC,BIC与CV做模型选择=====================================

%[peAIC,peBIC,AIC,BIC,c2AIC,c2BIC,c2CV,CV,CV_P] = FunModelABC(x,y)

%y表示的是lwage

%x表示的是hours,IQ,KWW,educ,exper,tenure,age,married,black,south,urban这11个变量

function [peAIC,peBIC,AIC,BIC,c2AIC,c2BIC,c2CV,CV,CV_P] = FunModelABC(x,y)

randn('seed',0541);%设置随机数种子

n = length(y);%总的样本量

nTest = 435; %选择435个样本做测试集

nTrain = n − nTest;%用剩余的样本做训练集

n1 = length(nTrain); %为了保证与AIC, BIC模型的训练集维度一致,CV模型的维度n1 = 935 − 435 = 500

CV = zeros(12,1000);%用来存放CV预测误差的求和

for k = 1:1000

%_________________( AIC,BIC数据准备 )__________________________________

Data = [y,ones(n,1),x];%构造的数据矩阵

yTrain = DataTrain(:,1);%训练集中的因变量y为训练集的第1列

XTrain = DataTrain(:,2:13);%训练集中的自变量x为训练集的第2到14列

yTest= DataTest(:,1);%测试集中的因变量y为训练集的第1列

XTest= DataTest(:,2:13);%测试集中的自变量x为训练集的第2到14列

X1= XTrain(:,1); X2= XTrain(:,1:2); X3= XTrain(:,1:3); X4= XTrain(:,1:4); X5= XTrain(:,1:5);

X6= XTrain(:,1:6);X7 = XTrain(:,1:7);X8= XTrain(:,1:8);X9= XTrain(:,1:9);X10= XTrain(:,1:10);

X11= XTrain(:,1:11);X12= XTrain(:,1:12);

%___________________ 模型1的AIC与BIC构建 _________________________________

hb1 = [(X1'*X1)\(X1'*yTrain);zeros(11,1)];

hsig21 = mean((yTrain - XTrain*hb1).^2);%模型1的sig2的极大似然估计

L1 = −nTrain*log(2*pi)/2 - nTrain*log(hsig21)/2 - nTrain/2;%模型1的极大似然函数

AIC(1,k) = −2*L1 + 2*2;%模型1的赤赤池信息准则，存储在AIC的第1行第k列

BIC(1,k) = −2*L1 + log(nTrain)*2;

%__________________模型2的AIC与BIC构建 ______________________________

hb2 = [(X2'*X2)\(X2'*yTrain);zeros(10,1)];

hsig22 = mean((yTrain − XTrain*hb2).^2);%模型2的sig2的极大似然估计

L2 = −nTrain*log(2*pi)/2 − nTrain*log(hsig22)/2 − nTrain/2; %模型2的极大似然函数

AIC(2,k) = −2*L2+ 2*3;%模型2的赤赤池信息准则，存储在AIC的第2行第k列

BIC(2,k) = −2*L2 + log(nTrain)*3;

%_________________ 模型3的AIC与BIC构建 ________________________________

hb3 = [(X3'*X3)\(X3'*yTrain);zeros(9,1)];hsig23 = mean((yTrain − XTrain*hb3).^2);

L3 = −nTrain*log(2*pi)/2 − nTrain*log(hsig23)/2 − nTrain/2;%模型3的极大似然函数

AIC(3,k) = −2*L3 + 2*4; BIC(3,k) = −2*L3 + log(nTrain)*4;

%_________________ 模型4的AIC与BIC构建 ________________________________

hb4 = [(X4'*X4)\(X4'*yTrain);zeros(8,1)];hsig24 = mean((yTrain − XTrain*hb4).^2);

L4 = −nTrain*log(2*pi)/2 − nTrain*log(hsig24)/2 − nTrain/2;

AIC(4,k) = −2*L4 + 2*5;BIC(4,k) = −2*L4 + log(nTrain)*5;

%_________________ 模型5的AIC与BIC构建 ________________________________

hb5 = [(X5'*X5)\(X5'*yTrain);zeros(7,1)]; hsig25 = mean((yTrain − XTrain*hb5).^2);

L5 = −nTrain*log(2*pi)/2 − nTrain*log(hsig25)/2 − nTrain/2;

AIC(5,k) = −2*L5 + 2*6; BIC(5,k) = −2*L5 + log(nTrain)*6;

%_________________ 模型6的AIC与BIC构建 ________________________________

hb6 = [(X6'*X6)\(X6'*yTrain);zeros(6,1)];hsig26 = mean((yTrain - XTrain*hb6).^2);

L6 = −nTrain*log(2*pi)/2 − nTrain*log(hsig26)/2 − nTrain/2;

AIC(6,k) = −2*L6 + 2*7;BIC(6,k) = −2*L6 + log(nTrain)*7;

%_________________ 模型7的AIC与BIC构建 ________________________________

hb7 = [(X7'*X7)\(X7'*yTrain);zeros(5,1)];hsig27 = mean((yTrain − XTrain*hb7).^2);

L7 = −nTrain*log(2*pi)/2 − nTrain*log(hsig27)/2 − nTrain/2;

AIC(7,k) = −2*L7 + 2*8;BIC(7,k) = −2*L7 + log(nTrain)*8;

%_________________ 模型8的AIC与BIC构建 ________________________________

hb8 = [(X8'*X8)\(X8'*yTrain);zeros(4,1)];hsig28 = mean((yTrain − XTrain*hb8).^2);

L8 = −nTrain*log(2*pi)/2 − nTrain*log(hsig28)/2 − nTrain/2;

AIC(8,k) = −2*L8 + 2*9;BIC(8,k) = −2*L8 + log(nTrain)*9;

%_________________ 模型9的AIC与BIC构建 ________________________________

hb9 = [(X9'*X9)\(X9'*yTrain);zeros(3,1)];hsig29 = mean((yTrain - XTrain*hb9).^2);

L9 = −nTrain*log(2*pi)/2 − nTrain*log(hsig29)/2 − nTrain/2;

AIC(9,k) = −2*L9 + 2*10; BIC(9,k) = −2*L9 + log(nTrain)*10;

%_________________ 模型10的AIC与BIC构建 ________________________________

hb10 = [(X10'*X10)\(X10'*yTrain);zeros(2,1)];hsig210 = mean((yTrain - XTrain*hb10).^2);

L10= −nTrain*log(2*pi)/2 − nTrain*log(hsig210)/2 − nTrain/2;

AIC(10,k) = −2*L10 + 2*11;BIC(10,k) = −2*L10 + log(nTrain)*11;

%_________________ 模型11的AIC与BIC构建 ________________________________

hb11 = [(X11'*X11)\(X11'*yTrain);0];hsig211 = mean((yTrain − XTrain*hb11).^2);

L11 = −nTrain*log(2*pi)/2 − nTrain*log(hsig211)/2 − nTrain/2;

AIC(11,k) = −2*L11 + 2*12;BIC(11,k) = −2*L11 + log(nTrain)*12;

%_________________ 模型12的AIC与BIC构建 ________________________________

hb12 = [(X12'*X12)\(X12'*yTrain)]; hsig212 = mean((yTrain − XTrain*hb12).^2);

L12 = −nTrain*log(2*pi)/2 − nTrain*log(hsig212)/2 − nTrain/2;

AIC(12,k) = −2*L12 + 2*13;BIC(12,k) = −2*L12 + log(nTrain)*13;

%________________ 关于AIC,BIC的12个模型的预测误差 _______________________

pe(1,k) = mean((yTest − XTest*hb1).^2); pe(2,k) = mean((yTest − XTest*hb2).^2);

pe(3,k) = mean((yTest − XTest*hb3).^2);pe(4,k) = mean((yTest − XTest*hb4).^2);

pe(5,k) = mean((yTest − XTest*hb5).^2);pe(6,k) = mean((yTest − XTest*hb6).^2);

pe(7,k) = mean((yTest − XTest*hb7).^2); pe(8,k) = mean((yTest − XTest*hb8).^2);

pe(9,k) = mean((yTest − XTest*hb9).^2); pe(10,k) = mean((yTest − XTest*hb10).^2);

pe(11,k) = mean((yTest − XTest*hb11).^2); pe(12,k) = mean((yTest − XTest*hb12).^2);

%=======================CV做模型选择======================================

%选用随机抽样的500个样本对CV进行数据处理，维度n1 = length(nTrain) = 500

%选用的数据是前面AIC,BIC模型中随机抽样的500个训练集样本DataTrain

%用DataTrain的数据集每次删除一个样本，用这个样本作为测试集，用剩下的样本做训练集，循环500次

%考察预测误差，循环过程1000次

for i = 1:n1

%____________________ CV数据准备______________________________________

y1Train = DataTrain(:,1);%取出DataTrain的第1列作为y1Train

y1Train(i,:) = []; %删除第y1Train中的第i行

y1Test = DataTrain(i,1);%用删除的y1Train中的那行作为测试，记作 y1Test

x1Train = DataTrain(:,2:13);%x1Train为中的第2列到13列

x1Train(i,:) = [];%删除x1Train中的第i行

x1Test = DataTrain(i,2:13);%用删除x1Train中的那行作为测试，记作x1Test

%_______________12个CV模型的变量数据____________________________________

X11 = x1Train(:,1); X21 = x1Train(:,1:2); X31=x1Train(:,1:3); X41 = x1Train(:,1:4);

X51 = x1Train(:,1:5); X61 = x1Train(:,1:6); X71 = x1Train(:,1:7); X81 =x1Train(:,1:8);

X91 = x1Train(:,1:9); X101 = x1Train(:,1:10); X111 = x1Train(:,1:11); X121 = x1Train(:,1:12);

%______________________ 12个CV模型的预测误差_____________________________

pe11(i) = (y1Test − x1Test(:,1)*((X11'*X11)\(X11'*y1Train)))^2;

pe21(i) = (y1Test − x1Test(:,1:2)*((X21'*X21)\(X21'*y1Train)))^2;

pe31(i) = (y1Test − x1Test(:,1:3)*((X31'*X31)\(X31'*y1Train)))^2;

pe41(i) = (y1Test − x1Test(:,1:4)*((X41'*X41)\(X41'*y1Train)))^2;

pe51(i) = (y1Test − x1Test(:,1:5)*((X51'*X51)\(X51'*y1Train)))^2;

pe61(i) = (y1Test − x1Test(:,1:6)*((X61'*X61)\(X61'*y1Train)))^2;

pe71(i) = (y1Test − x1Test(:,1:7)*((X71'*X71)\(X71'*y1Train)))^2;

pe81(i) = (y1Test − x1Test(:,1:8)*((X81'*X81)\(X81'*y1Train)))^2;

pe91(i) = (y1Test − x1Test(:,1:9)*((X91'*X91)\(X91'*y1Train)))^2;

pe101(i) = (y1Test − x1Test(:,1:10)*((X101'*X101)\(X101'*y1Train)))^2;

pe111(i) = (y1Test − x1Test(:,1:11)*((X111'*X111)\(X111'*y1Train)))^2;

pe121(i) = (y1Test − x1Test(:,1:12)*((X121'*X121)\(X121'*y1Train)))^2;

end

%_______________CV预测误差求和__________________________________________

Loss = [sum(pe11);sum(pe21);sum(pe31);sum(pe41);sum(pe51);sum(pe61);sum(pe71);sum(pe81);sum(pe91);sum(pe101);sum(pe111);sum(pe121)];

CV(:,k) = Loss;

end

% _______________选出12个模型中的最小的AIC与BIC __________________________

%________________计算CV的12个模型1000次中每个模型被选中的比例______________

for h = 1:12

CV_P(h) = mean(c2CV==h);

end

%__________________最小AIC,BIC,CV对应位置的预测误差 ______________________

for k = 1:1000

peAIC(k) = pe(c2AIC(k),k);peBIC(k) = pe(c2BIC(k),k);peCV(k) = pe(c2CV(k),k);

end

%================== 从x中无放回的抽取k个样本 ================================

function [x, Xre, idk ] = smplwor(X,K)

for k = 1:K

idk(k) = unidrnd(Nk);%从1到Nk的正整数中产生1个均匀随机整数，作为角标

x(k,:) = X(idk(k),:);%取出原始数据X对应角标的那行存储在x的第k行中

X(idk(k),:) = [];%删除原始数据X所抽走的那行

Nk = Nk - 1;%无放回抽样，每次抽一行后都减掉1

end

Xre = X;%把已经删除了抽样行的矩阵记作Xre，即抽样剩下的样本矩阵的样本矩阵