1. 引言
随着网络技术的高速发展和互联网技术的普及,网络已经成为人们工作、生活必不可缺的一部分 [1]。传统的网络流量预测主要凭借主观经验,根据历史数据和个人经验进行流量的预测判断,该类方法误判的几率较大,不能够对流量变化趋势做出准确判断,预测结果较实际数据存在明显偏差。如果基于大量历史数据并且实时掌握目前网络状况,进行流量预测,其结果会更加可靠,因此提出了网络流量预测分析模型。
近年来,许多流量预测模型被提出,其中包括统计与回归方法 [2],基于流量的方法 [3] 和机器学习方法 [4]。目前被广泛认可的自回归积分滑动平均模型(Autoregressive integrated moving average model,简称ARIMA),已于20世纪70年代应用在网络安全领域,目的是预测网络系统的状况,并且逐渐成为新的预测模型的比较对象。ARIMA在数据规则变化时表现出良好性能,但是当数据不规则变化时,预测的误差较大。同时随着计算性能逐渐提高,传感器技术的成熟,能够感知采集大量数据,由此引发的“数据爆炸”的问题越来越受到重视,传统的方法由于维度的局限性难以适应现在预测需求,因此目前急需新的处理大数据的预测模型。
上述研究方法虽然能初步地解决流量预测的问题,但是没有考虑到内部深层细粒度特征。随着机器学习技术的发展,深度学习以其强大的特征提取能力,基于深度学习的预测模型逐渐成为新趋势。到目前为止,深度学习技术已经在自然语言处理、语音识别和计算机视觉领域取得显著成功,并向其他领域应用广泛扩展,其中时间序列分析为新的扩展方向之一。网络流量预测分析可以抽象成时间序列问题,目前循环神经网络模型(Recurrent neural network,简称RNN)被广泛认可,但是根据以往研究表明,传统的RNN方法性能难以满足需求,对10分钟后的数据难以预测,为此本文提出将长短期记忆网络模型(Long short-term memory,简称LSTM)用于网络流量的预测,该方法具有较高的准确性,与ARIMA模型对比性能提高近70%。
2. 流量预测
流量预测作为网络安全的重要研究方向之一可以抽象为时间序列预测问题,时间序列预测虽然作为机器学习的重要领域之一,但与其它机器学习问题不同,关键区别在于固定的数据序列约束以及提供的约束条件。时间序列预测问题涉及许多时间分量,而这往往是问题解决的难点,并且不能简单地使用机器学习算法解决。时间序列预测为根据当前和过去采集到的数据,分析预测出未来几分钟到几个小时的可能状况。此类问题与网络流量预测问题、交通预测问题十分类似,两类都可以归结为时间序列预测的研究问题,随着深度学习的高速发展,为两类问题的解决提供新的研究思路和方法。
人工神经网络(Artificial neural network,简称ANN)自20世纪80年代以来被广泛应用于时间序列预测问题中,众所周知的ANN网络模型有以下几种:多层感知器(Multi-layer Perceptron,简称MLP)、循环神经网络、径向基网络(Radial basis function network,简称RBFN),以及其他多种模型。ANN出现之前,线性统计方法为预测的主流方法,但是该方法存在严重局限性,不能够捕获到复杂现实世界中的非线性关系 [5],同时Makridakis组织的一次大规模的预测竞赛的结果也表名,数据中存在不同程度上的非线性,不能通过线性统计方法处理。然而ANN作为广义非线性预测模型,能一定程度上捕获数据中的非线性关系,因此得到广泛的普及。随着科技进步,机器计算能力大幅度提升,Hinton于2006年提出深度学习概念 [6],深度学习提供的高维度空间以及低维嵌套结构,有效解决了非线性降维方法无法解决的问题。Enzo Busseti等 [7] 创新性的将深度学习应用于时间序列预测中,探索出不同模型预测精度不同的结论。
RNN同样作为目前解决时间序列预测的主流方法之一,也可应用于网络流量预测问题中,由于RNN的提出,目前许多模型都是基于RNN的改进。但是RNN在面对长期时间序列表现出来的性能欠缺误差较大的问题,迫使我们寻找更好的方法,由此提出将LSTM模型应用在时间序列预测问题中。李高盛等人于2019年对LSTM模型进行相关研究 [8],LSTM神经网络模型由三层构成,其中隐藏层由内存块组成,并且能够通过训练方法自动确定参数,与现有的方法相比无疑是一种创新点。
3. 相关工作
流量预测具备时空复杂性,未来流量的预测需要大量数据作为基础,但是因为设备流动性大的原因,数据的采集往往较为困难。本节将首先介绍数据集获取的方法,然后详述涉及的RNN和LSTM模型的相关知识。
3.1. 数据的获取
网络数据的获取是指以一定时间为周期,通过采集设备获取特定区域内的流量数,并进行处理和存储。由于设备流动性大的问题,采集的数据仅能在一定程度上反应此时的网络流量,但是已然具有参考价值。目前有多种方式获取网络流量数据,本数据集的获取方式为通过WiFi和移动网络信息获取实时流量。通过移动设备连入网络的数量评估区域内流量,该技术不需要昂贵的基础设施,成本低廉。
3.2. RNN模型
传统神经网络相邻层之间的节点完全连接,而同一层的节点没有任何联系,由于节点之间需要相互交互,导致这种类型的网络模型在处理时间序列预测问题上性能欠佳。RNN中的隐藏单元可以接收到先前状态对当前状态的反馈。图1展示了一个基本的RNN架构。
在这种结构中,输入向量逐次送入RNN中,而不像传统神经网络一样采用固定数量的输入方式,同时能够根据实际情况确定RNN的深度。最终的输出结果不仅受当前输入值的影响,还受先前隐藏层输出结果的影响。以下用数学模型表示:
(1)
公式中
表示输入变量,
、
和
为权重矩阵,
和
是偏差向量,
和g为Sigmoid函数,
、
和
为临时变量,
为输出变量。损失函数如下:
(2)
其中
表示真实输出。
处的输出由
处的输入和历史数据共同决定。由于梯度的问题,RNN模型的精度随时间的推移下降,最终导致输出误差较大。
3.3. LSTM模型
LSTM模型在RNN模型的基础上进行改进,通过将隐藏层作为记忆单元,能够解决短期和长期时间序列的相关性问题。图2给出记忆单元的结构图,存储单元位于整个记忆单元的核心处,用红色圆圈表示。输入为已知数据,而输出则是预测的结果。在记忆单元中存在三个门,分别为输入门、遗忘门、输出门,通过绿色圆圈在图中标识。每个单元的状态用
表示,每个门的输入由预处理数据
和先前
状态组成。蓝色点代表汇聚点,虚线是前一状态函数。以记忆单元中信息的流动为基础,状态的更新和输出可以归纳为公式3:
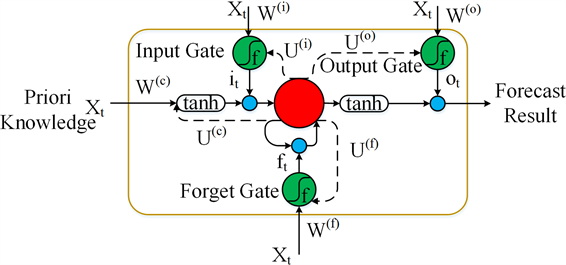
Figure 2. Design of the memory unit of LSTM
图2. LSTM记忆单元设计
(3)
公式中的
表示Hadamard乘积,
、
和
表示三种不同的门,
为新状态的记忆单元,
为最终状态的记忆单元,
是最终输出的存储单元。
、
、
、
、
、
、
和
为系数矩阵。
经由不同功能门后,LSTM记忆单元可以捕获短期和长期时间序列中复杂的相关特性,相比RNN模型性能明显提高。
4. 实验分析
4.1. 数据集分析
实验数据集来源于2018年某火车站整个候车室的设备流量信息,候车室提供WiFi接入点,每个数据采集点以一分钟为周期采集连入的设备量,通过该数据反应此时网络数量。整个数据集由1000组数据组成,时间从2018年9月10日18时55分开始到2018年9月11日11时34分结束,图3为数据集的折线图,反应出数据的变化趋势。从图中反应的网络流量信息中可以看出,设备数量从开始到9月10日20时13分达到峰值,随后数量逐渐减少,至9月11日4时26分到达谷底,后又呈逐渐升高的趋势,由此可以看出数据集不是固定的,在此进一步分析序列的自相关性如图4所示,图中表现了前210个点之间存在明显的正相关性,210到630的数据存在负相关性,剩下数据相对而言相关性较弱。
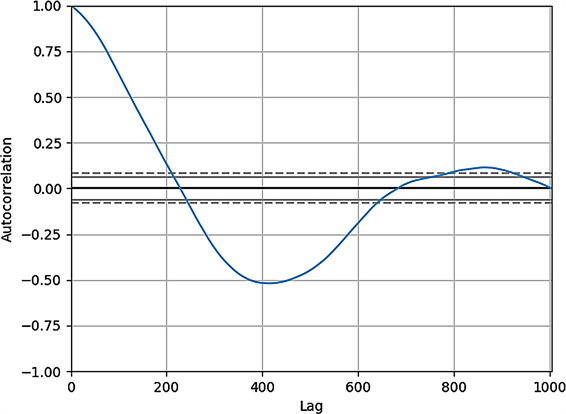
Figure 4. Autocorrelation plot of data set
图4. 数据集自相关图
4.2. 评估标准
本实验采用均方误差(Mean squared error,简称MSE)和均方根误差(Root mean square error,简称RMSE)评估模型的精确度,预测模型越准确MSE和RMSE的值越小,因此许多预测模型会以MSE或RMSE的值作为衡量模型好坏的标准。
(4)
4.3. 实验结果
本次实验的实验环境为:CPU为Intel core i5-9400F 2.90 GHz,操作系统Windows10 16位,内存为16GBDDR。本次实验首先用LSTM模型在不同迭代次数参数下的结果,然后列举ARIMA模型在不同(p, q, d)下MSE的误差值,选取最优LSTM模型和最优ARIMA模型进行比较。
设置不同迭代次数,LSTM预测出模型的准确度不同,若迭代次数少LSTM模型可能还未到平稳状况就被迫中止,相反若迭代次数多,不止程序运行时间过长,并且会影响最后模型的准确度。图5给出在50、100、150、200、250、300、350、400迭代次数下LSTM模型的RMSE误差盒式图,从盒式图中可以看出,当迭代次数为150时RMSE的平均值最小为19.992,由此将该参数设定为LSTM模型的最优参数。
ARIMA作为经典的时间序列预测模型,算法和参数调整方面已较为成熟,在此列举不同(p, q, d)参数下ARIMA模型MSE误差值,见表1。表中可以看出,针对此数据集,ARIMA参数在(2, 1, 1)情况下性能最优,因此选择参数(2, 1, 1)的ARIMA模型作为最优ARIMA模型。
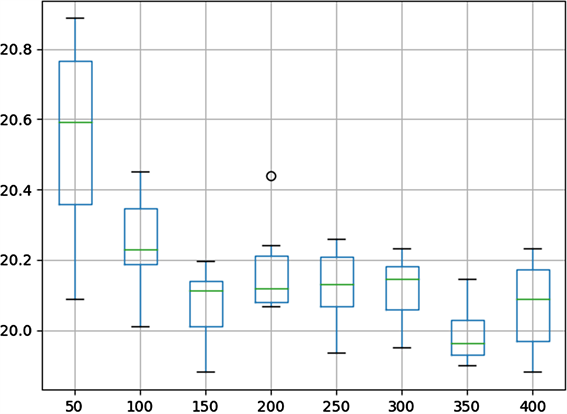
Figure 5. Box and whisker plot summarizing epoch results
图5. 不同迭代次数误差值的盒式图

Table 1. The result of ARRIMA model
表1. ARRIMA模型运行结果
上面分别介绍了LSTM最优模型的RMSE误差和ARRIMA最优模型的MSE误差,由于RMSE和MSE之间存在以下规则,
(5)
在此将LSTM模型取得的RMSE误差值转化成MSE误差值,结果为399.640,由此可以算出LSTM模型相较ARRIMA模型,性能提高69.64%。图6给出LSTM模型的预测曲线,蓝色为原始数据集,橙色为预测模型给出的预测数据集。
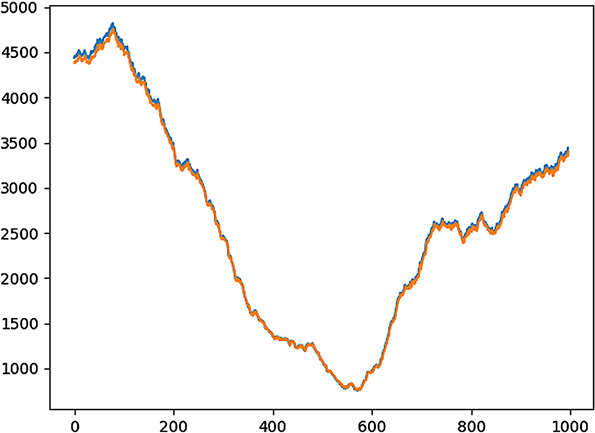
Figure 6. Line chart of LSTM model prediction
图6. LSTM模型预测图
5. 总结与展望
本文创新性地提出了一种网络流量预测模型,实验表明,方法可以很好地拟合数据集的流量曲线,验证出LSTM模型相比ARIMA模型性能提高明显,并能准确地预测出未来一段时间的变化趋势。网络流量预测模型的建立受各种因素影响,因此在未来工作中,作者将在更为广泛的数据集上应用,构建更加完善准确的网络流量预测模型。