智能网络电力组织架构、需求预测与传输路由决策

Intelligent Network Power Organization Structure, Power Demand Prediction and Transmission Routing Decision Strategy

摘要: 为了能确保电力系统能够稳定运作，电网的调节能力以及对于各种能源本身电力间歇性、多变性以及不确定性的补偿是必须的，以避免在中心INA故障时不会影响接受端系统的安全性与当地系统的稳定性。文中提出如何建构自动组织的电力输送架构，以及利用灰色理论GM(1,1)模式来预测每个智能网络代理(INA)分配所管理的电力分配输送能力的预测模型。最后也提出当一个或两个中心INA故障时，其所原先提供的这些电力如何落到其他中心INA来输送，以及对电力输送的路由(路径)采用最小生成树Prim的决策路由。其中我们也提到当建设这些系统时所必须考虑的一些条件。

Abstract: In order to ensure the stable operation of the power system, the regulation ability of the grid and compensation for the intermittent, variability and uncertainty of the power of various energy sources are necessary to avoid affecting the safety of the receiving end system and the stability of the local system when the central INA fails. In the article, we proposed the strategies about how to construct an automatically organized power transmission architecture. We also use the GM(1,1) model in grey theory to predict each intelligent network agent (INA) to allocate the management power distribution and transmission capacity prediction model. Finally, we also proposed the routing method and the method to redistribute the power when one or two central INA failures. The power transmission routing path will be decided by Prim, a minimum spanning tree, decision routing strategy. We also mentioned some conditions that must be considered when building these systems.

1. 引言

随着温室效应造成环境气候逐渐恶劣，以及光伏组件以及储能电池价格趋于便宜 [1]，因此未来的民众极有可能实现电量自给自足。然而在此之前，电力的主要供给来源还是在于公用电力公司的基础传输电网。一般公用电网对于来自不同能源的电力可能因为不同能源本身的属性造成间歇供电或中断供电(例如太阳能发电的电力取决于光照度强度，而光照度强度则随着季节更替，灰尘、云层、霜雪、以及铺设地点而有所变动)，也可能因为能源的输出量不如预期(例如风力发电则因风力、风速难以预测其电力传输)。为了能确保电力系统能够稳定运作，电网的调节能力以及对于各种能源本身电力间歇性、多变性以及不确定性的补偿是必须的，以避免在输电线故障时不会影响接受端系统的安全性与当地系统的稳定性 [2]。

2003年IEEE 1547 [3] 针对分布式能源制定了标准规范，其主要目的就是为了减少不同能源之间对电网造成不良的影响。因为分布式电源是将不同电源接入一般公用电网，所以当电网出现供电异常时，分布式电源会依据保护设施对电网的电压以及运作周期做出适当的响应，且能够在一定的电压范围和时间间隔之内不会脱离电网而继续供应电力，以避免电网造成安全稳定带来极大的风险 [4]。

电力系统互联是能够让相邻电力公司之间进行电力交换，以达到全系统的发电电力能够实时与系统负荷需求相互配合，使系统的电力扰动可以维持在一定的可接收的波动变化准位之间。在紧急状态下，互联电力系统可以共享备用储存电力。为了完成系统电力负荷需求互相配合，因此每个区域电力系统必须紧密地追踪它们的电力总负荷量，将系统维持在一定的波动范围内。为了能够降低连锁停电的风险，解决能源电网上的安全稳定，提高电力传输效率，以及提高电力系统韧性，因此更具有智慧化的电网 [5] 便应运而生。

智慧电网 [6] 的基本需求是要能够结合各种不同的能源供应，且须可以预测和遥感电力系统运作的状态以及可以依据预测与实际情况自动重新建构电网，防止或降低停电的潜在风险，同时满足消费者的需求。在 [7] 中智能配电网切割成许多胞(cell)，而两个胞之间可以依据事先规划来进行彼此之间的电力交换，而在每一个胞之中可以收集系统讯息与信息交换分享，以及对局部控制做出自主决策的智能网络代理来分配所管理的电力。虽然每一个胞可以是一个微网，但是这样的方式之中每一个胞的INA只有透过一主干电力网线将电力传向另一个胞的INA。也就是说它能够分享的空间扩展率并不足够，这也就造成对于实现电力互联让彼此之间都能够分享所拥有的电能无法彻底地达成。

在 [8] 中提出GRIP (a smart grid with intelligent periphery for the future)的智慧电网概念，他是属于一种层级结构的输电网管理系统。在这种架构中，一个核心的输电网群之间包含了很多个变电站。如何减少这些变电站，但却能满足发电计划确是一个极为主要的设计点。提高用户高阶入电量的可靠性，以及降低电力传输的损耗性也是一个议题。一般电网的输送距离较长，所以电网传输损耗较大。为了维持电力净功率的平衡，发电调度与安排也牵涉到传输网络路由(routing path)的规划与自动调节。

本文结构如下：在第二章我们将提出蜂巢式智能电网的系统架构观念。在第三章中，电力供需的电力预测则以灰色理论GM(1,1)模式来进行预测用户所需要的电量。在第四章则提出智能网络电力输送路由调节算法。最后于第五章做一总结。

2. 蜂巢式智能电网的系统架构

配电系统连接了配电变电站，以及使用电力的用户。在电力供电中为了减少电能于传输过程中的电力损耗，一般会以升压变压器将电力提高成高电压以减少电流，再将高压电网的输送线连接到高压变电站。INA主要功能包括电力保护、分布式发电与储能设备、以及分布式电源配电调度等功能 [9]。在本智能电网架构系统中我们是以蜂巢式的架构为主。每一个蜂巢与另一个蜂巢相连接的INA称为边缘INA，而每一个蜂巢的中心INA称之为中心INA。每一个中心INA可以利用主干配电线与本地发电电力网相连接，再依据蜂巢边缘INA的用电需求以一定额度的备电量比例供给每一个边缘INA的电力。当然边缘INA以及中心INA的电力可以是不同的电力来源所组成的。很显然地，每一个边缘INA的电力供给来源最大是来自N个中心INA (在图1中，N = 4)。由图1中，为了避免边缘INA与中心INA的脚色重迭，不同颜色的蜂巢各自组成一个电力供应网，只有在该颜色区域中心的INA才是中心INA，其他的都是属于边缘INA。而第i个蜂巢的第j个边缘INA (令为 ${\text{INA}}_{i,j}$ )电力与其他蜂巢k的中心INA (令为 ${\text{CINA}}_k$ )电力供给关系则为

$P_{i,j}={\displaystyle \underset{k=1}{\overset{N}{\sum }}{P}_k{\alpha }_k}+\widetilde{P_{i,j}}$

其中 ${\alpha }_k$ 为来自第k个蜂巢中心之INA包含提供给第i个蜂巢的第j个边缘INA备电能力在内的电力供应权重； $\widetilde{P_{i,j}}$ 则为第i个蜂巢中第j个边缘INA自己由不同电力能源所产生的总电力。

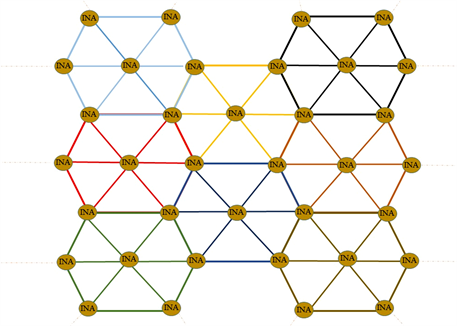
Figure 1. The cellular smart grid architecture

图1. 蜂巢式智能电网架构

因为每一个蜂巢中心INA最大可提供M个(在这里M = 6)边缘INA的电力，但是其所能提供的电力最大值则为中心INA自身所拥有的电力储存值，因此

${\displaystyle \underset{m=1}{\overset{M}{\sum }}{P}_{k,m}{\alpha }_{k,m}}\le \max \left(P_k\widetilde{P_{i,j}}\right)$

且(i, j) = (k, m)的意思是指第i个蜂巢的第j个边缘INA就是第k个蜂巢的第m个边缘INA。

电力系统安全性 [10] 是电力系统调度的一个重要议题，其主要是避免电网在失去一个或两个中心INA之后仍然能够正常的运作。在这里我们必须考虑到某一个中心INA其所能供应的电力在边缘INA电力需求突然增加时，无法再加以额外提高电力的供应能力，此时考虑要能使电网仍然能够正常运作。假设 ${\alpha }_k$ 是来自 ${\text{INA}}_{i,j}$ 的电力预测需求，而于 ${\text{CINA}}_k$ 计算后所能提供的决策供电权重。为了避免 ${\text{INA}}_{i,j}$ 中电力不足造成供电不稳定的风险，所以必须满足

${\displaystyle \underset{k=1}{\overset{N}{\sum }}{\alpha }_k}\ge 1$

而 ${\text{INA}}_{i,j}$ 所接收的电力若超过总需求量 ${\displaystyle {\sum }_{k=1}^N{\alpha }_k}=1$ 时，则其余的电力能源均可储存在自己的储能设备中，以减少 ${\text{INA}}_{i,j}$ 中供电不稳定的风险。当然， ${\text{INA}}_{i,j}$ 所需的能源需求则可以 ${\text{CINA}}_k$， $k\in \left\{1,2,3,\cdots ,N\right\}$，互相沟通，而 ${\text{CINA}}_k$ 之间也可以互相依各蜂巢中心INA目前的电力供应能力互相协调，以做出最好的调配。事实上，如果有需求的话，我们也可以规划 ${\text{INA}}_{i,j}$ 与 ${\text{INA}}_{i,r}$ 之间的电力互相调配供给。

3. 预测理论

智慧电网需要持续不断地预测需求变化，并且评估变化中的收益与成本，针对预测理论本节以灰色理论GM(1,1)模型来作为探讨的依据。灰色理论是研究少量数据以及具有贫穷讯息下问题不确定的方法，它是在1982年由邓聚龙教授所建立的。此一理论产生之后便受到极大的关注。日常生活中不确定的系统是常常存在的，通常我们对某一属性的归类、讯息的预测、结构讯息的完整性、以及边界讯息的不确定性都是时常产生的。灰色预测 [11] 就是在一定范围之中的变化对系统的行为特征发展趋势的时间序列进行预测，目前最常用的灰色模型为GM(1,1)。假设有作为预测对象的数据列

$X^{\left(0\right)}=\left\{X^{\left(0\right)}\left(i\right),i=1,2,\cdots ,n\right\}$

为一非负数的单调原始资料列。为了建立灰色预测模型，首先对原始数据列作一次累加生成(记为1-AGO)，得到一新的数据列为

$X^{\left(1\right)}=\left\{X^{\left(1\right)}\left(k\right),k=1,2,\cdots ,n\right\}$

其中

$X^{\left(1\right)}\left(k\right)={\displaystyle {\sum }_{i=1}^k{X}^{\left(0\right)}\left(i\right)}=X^{\left(1\right)}\left(k-1\right)+X^{\left(0\right)}\left(k\right)$ (1)

假设 $X^{\left(1\right)}$ 的紧邻平均值生成序列为

$Z^{\left(1\right)}=\left(z^{\left(1\right)}\left(1\right),z^{\left(1\right)}\left(2\right),z^{\left(1\right)}\left(3\right),\cdots ,z^{\left(1\right)}\left(n\right)\right)$ (2)

其中

$z^{\left(1\right)}\left(k\right)=\frac{1}{2}\left[x^{\left(1\right)}\left(k\right)+x^{\left(1\right)}\left(k-1\right)\right]$, $k=2,3,4,\cdots ,n$ (3)

此时可以获得GM(1,1)模型的基本形式为

$x^{\left(0\right)}\left(k\right)+a{z}^{\left(1\right)}\left(k\right)=b$ (4)

分别将 $k=2,3,4,\cdots ,n$ 代入得

$\{\begin{array}{l}{x}^{\left(0\right)}\left(2\right)+a{z}^{\left(1\right)}\left(2\right)=b\\ x^{\left(0\right)}\left(3\right)+a{z}^{\left(1\right)}\left(3\right)=b\\ ⋮\\ x^{\left(0\right)}\left(n\right)+a{z}^{\left(1\right)}\left(n\right)=b\end{array}$ (5)

或

$\{\begin{array}{l}{x}^{\left(0\right)}\left(2\right)=b-a{z}^{\left(1\right)}\left(2\right)\\ x^{\left(0\right)}\left(3\right)=b-a{z}^{\left(1\right)}\left(3\right)\\ ⋮\\ x^{\left(0\right)}\left(n\right)=b-a{z}^{\left(1\right)}\left(n\right)\end{array}$ (6)

若以矩阵的方式加以表示，令矩阵Y以、矩阵B、以及矩阵A分别如下所示：

$Y=\left[\begin{array}{c}{x}^{\left(0\right)}\left(2\right)\\ \begin{array}{c}{x}^{\left(0\right)}\left(3\right)\\ ⋮\end{array}\\ x^{\left(0\right)}\left(n\right)\end{array}\right]$, $B=\left[\begin{array}{c}-z^{\left(1\right)}\left(2\right),1\\ \begin{array}{c}-z^{\left(1\right)}\left(3\right),1\\ ⋮\end{array}\\ -z^{\left(1\right)}\left(n\right),1\end{array}\right]$, $A=\left[\begin{array}{c}a\\ b\end{array}\right]$

此时方程式(6)可以用矩阵的方式表达成为

$Y=BA$ (7)

现在我们要估计出参数a及参数b的值。令 $\hat{A}$ 为其估计值数组，所以可得

$\hat{A}={\left(B^{\text{T}}B\right)}^{-1}{B}^{\text{T}}Y$ (8)

此时在GM(1,1)模型中 $x^{\left(0\right)}\left(k\right)+a{z}^{\left(1\right)}\left(k\right)=b$ 中所建立的时间响应序列为

${\hat{X}}^{\left(1\right)}\left(k+1\right)=\left(X^{\left(0\right)}\left(1\right)-\frac{b}{a}\right){\text{e}}^{-ak}+\frac{b}{a}$ (9)

接着由 ${\hat{X}}^{\left(1\right)}$ 还原为原来的 ${\hat{X}}^{\left(0\right)}$。因为

${\hat{X}}^{\left(1\right)}\left(k\right)={\displaystyle {\sum }_{i=1}^k{\hat{X}}^{\left(0\right)}\left(i\right)}={\displaystyle {\sum }_{i=1}^{k-1}{\hat{X}}^{\left(0\right)}\left(i\right)}+{\hat{X}}^{\left(0\right)}\left(k\right)={\hat{X}}^{\left(1\right)}\left(k-1\right)+{\hat{X}}^{\left(0\right)}\left(k\right)$ (10)

所以可得

${\hat{X}}^{\left(0\right)}\left(k\right)={\hat{X}}^{\left(1\right)}\left(k\right)-{\hat{X}}^{\left(1\right)}\left(k-1\right)$ (11)

以台湾经济部能源局 [12] 所提供的每年能源需求表，如表1，则利用灰色GM(1,1)我们可以求得

Table 1. Electricity demand of Taiwan in 1990~108

表1. 台湾90年度至108年度用电需求量

此时求得的时间响应序列为

${\hat{X}}^{\left(1\right)}\left(k+1\right)=\left(X^{\left(0\right)}\left(1\right)+14609593.81\right){\text{e}}^{0.0147k}-14609593.81$

根据公式(11)可以得到109年度所预测的需求电量为277578.42。我们提到原始序列为 $X^{\left(0\right)}=\left\{x^{\left(0\right)}\left(1\right),x^{\left(0\right)}\left(2\right),\cdots ,x^{\left(0\right)}\left(n\right)\right\}$，而对应所建立的时间响应序列所对应的估测值为 ${\hat{X}}^{\left(0\right)}=\left\{{\hat{x}}^{\left(0\right)}\left(1\right),{\hat{x}}^{\left(0\right)}\left(2\right),\cdots ,{\hat{x}}^{\left(0\right)}\left(n\right)\right\}$。这两个序列之间的相对应元素均存在一误差，若定义残差序列 ${ϵ}^{\left(0\right)}=\left\{ϵ\left(1\right),ϵ\left(2\right),\cdots ,ϵ\left(n\right)\right\}$ 为原始序列 $X^{\left(0\right)}$ 与估测序列 ${\hat{X}}^{\left(0\right)}$ 之间的误差序列，则

$ϵ\left(k\right)=x^{\left(0\right)}\left(k\right)-{\hat{x}}^{\left(0\right)}\left(k\right)$, $k=1,2,3,\cdots ,n$ (12)

根据公式(12)可以求得

$\begin{array}{c}ϵ=[0.0\text{87257}0\text{7}0.0\text{493}0\text{5}0\text{2}0.0\text{1938745}0.00\text{6587}0.0\text{2655337}0.0\text{4295876}\\ 0.00\text{917243}0.0\text{41647}0\text{7}0.0\text{1575125}0.0\text{214}0\text{313}0.000\text{2}0\text{862}0.00\text{711254}\\ 0.00\text{793726}0.0\text{1386559}0.00\text{56446}0.00\text{267592}0.00\text{734}0\text{48}0.0\text{1284294}]\end{array}$

很显然地，原始值与估计值之间的误差非常小，所以其预测准度非常高。

4. 电网络由传输

当第x个中心INA故障时，如图2所示，则第x个中心INA所负责的供电量便得分配到相邻蜂巢(记为d = 1)的中心INA中。因为每一个中心相邻的INA同时也供应了边缘INA，因此，很显然地，若令 $D_{s-\left\{x\right\}}$ 代表第x个蜂巢中心INA故障导致无法供应足够的电力时，第s个蜂巢之中心INA所必须提供第x个蜂巢第j个边缘INA的电力，此时

$D_{s-\left\{x\right\}}=\left(\underset{j\in x}{{\displaystyle \sum }}{\alpha }_{x,j}{\text{INA}}_{x,j}\right)+D_{s0}$

也就是第s个蜂巢中心INA的电力供电量为

$D_{s-\left\{x\right\}}\le C_s$

其中C_s为第s个蜂巢中心INA所能提供的最大电力供应储存量，而 $D_{s0}$ 则是代表原先在第x个蜂巢中心INA没有故障下，第s个蜂巢中心INA的电力供电量。

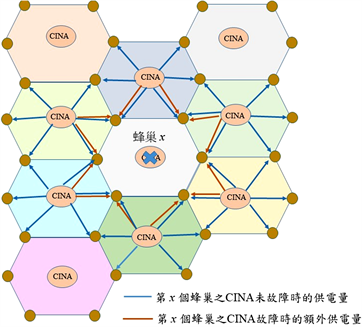
Figure 2. Schematic diagram of the cellular power transmission when the xth cellular center INA fails

图2. 第x个蜂巢中心INA故障蜂巢供电示意图

要特别注意的是：有可能协调后的电力供给量会由于第s个蜂巢中心INA (CINA)因为要求的总能量超过他所能提供的最大储存电力而造成无法加以提供，所以必须经由离该蜂巢x距离s次近中心CINA (记为d = 2之CINA)来加以提供。因此每一个CINA本身电力是互相独立的，此时就必须透过边缘INA来加以执行这项任务。此时必须考虑两个因素，即是离该蜂巢x距离s次近中心CINA所能提供的电力容量，以及边缘INA的电力接收能力。此时藉由边缘INA将d = 2之CINA的供应电力输送到 ${\text{INA}}_{x,j}$ 的路径选择问题，则可以视为每个d = 2之CINA的最小生成树问题。

某个无方向图的生成树是由原图的所有顶点和部分边缘线的集合所构成的子图。而生成树中的边线是指能将各顶点连接成为树状结构，而集合中的边线不准让途中有形成回路的现象。对于图结构而言，生成树可能不只一种，而我们则想要找出途中边线权重之合为最小的生成树 [13]，亦即要找出最小生成树。至于边缘的权重则可以令为该接收INA目前电力所使用的量。在没有任何CINA故障的情况下，所有蜂巢边缘INA的电力是由原CINA所供应的，此时可以令边线的权重为无限大，如此作法便不会造成邻近蜂巢需支持邻近蜂巢的电力供应，意思就是不会有最小生成树的产生。

因为只考虑相邻的边线，且只会反复执行在可选的边线之中选择权重值最小的边线操作，所以我们可以采用普里姆(Prim)最小生成树算法。Prim算法 [13] [14] [15] [16] 是贪婪算法的一种，在这里要维护两个顶点集，其中一个是已经被访问过的顶点，另一个是未被访问的顶点。我们再给定图的距离第x个蜂巢(故障蜂巢CINA) d = 2的中心原点开始，持续在答案树中添加最小权重的边，直到通达目标的边缘INA为止。有关Prim算法的计算如下所示：

初始：假设R为一个具有n个顶点的图树，M为各个顶点对应之间每顶点之间的路径权重矩阵。

步骤1：选择M中的最小项，记为m_i,j，且所对应的顶点中，相对应于第i行的顶点为a，相对应于第j列的顶点为b。

步骤2：路由顶点替换。

1) 将矩阵第i行的元素以下列法则替换

$m_{i,k}=\{\begin{array}{l}{m}_{i,k},m_{j,k}=0\\ m_{j,k},m_{i,k}=0\\ \min \left(m_{i,k},m_{j,k}\right),m_{i,k}\ne 0且m_{j,k}\ne 0\\ 0,m_{i,k}=m_{j,k}=0\end{array}$

2) 将矩阵第i列的元素以下列法则替换

$m_{k,i}=\{\begin{array}{l}{m}_{k,i},m_{k,j}=0\\ m_{k,j},m_{k,i}=0\\ \min \left(m_{k,i},m_{k,j}\right),m_{k,i}\ne 0且m_{k,j}\ne 0\\ 0,m_{k,i}=m_{k,j}=0\end{array}$

删除第i行和第j而得到新矩阵M'。

步骤3：令MßM'，重复步骤1以及步骤2计算，直到只剩下单独的一个顶点为止。每一个阶段计算中保留原始顶点集合的每项纪录，如此的纪录便可以生成最小生成树。

当电网启动电力网络路由时，则CINA与边缘INA会有特定的网络协议互相通知。当路由建立后，电力输送便会依据最小生成树及所提供的电力分配输送到相关的边缘INA之中。至于d = 2的INA要如何知道则有几种方式可以获得。1) 智慧网规划时各CINA已经建立起数据库了；2) 由供应的蜂巢CINA之上一层INA来指挥下命令完成；3) 由各边缘INA彼此交换CINA信息而得。

当有相邻的两个蜂巢CINA故障时，如图3所示，会产生由边缘INA r将电力输送到边缘INA a及边缘INA c的情况。此时为了能同时将电力传送到边缘INA a及边缘INA c则势必建立出电力线段be要能承受电力量，另外，我们如果把以INA r为起点的最小生成树与n为起点的最小生成树看成是两个独立的不同图，则就没有所谓的问题产生了。

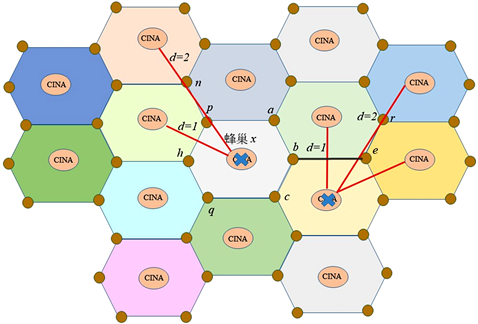
Figure 3. Schematic diagram of power transmission routing when two cellular CINAs fail

图3. 两个蜂巢CINA故障之电力供应路由示意图

一个具有n个顶点(边缘INA)的图G = (V, E)，若w_i,j表示顶点v_i与顶点v_j之间的电路传输权重，T为G的生成树。因为两边缘INA (顶点v_i与顶点v_j)之间的电力传输电力为P_i,j不能超过其最大电力容量C_i,j，所以电力路由策略为：

$\min w(\; T\; )$

Such that

$D_{s-\left\{x\right\}}=\left({\displaystyle \underset{j\in x}{\sum }{\alpha }_{x,j}{\text{INA}}_{x,j}}\right)+D_{s0}\le C_s$

$w_{i,j}=\{\begin{array}{l}{P}_{i,j}\le C_{i,j},\left({\text{INA}}_i,{\text{INA}}_j\right)\in E\\ 0,\left({\text{INA}}_i,{\text{INA}}_j\right)\notin E\end{array}$

5. 结论

本文涉及主动配电划分与实现配电自动化的多个子网协调控制，同时也提出灵活可重构的配电网络拓朴，实现智能电网自愈与优化的功能。其中自愈功能包括权重重构、故障定位与隔离 [17]。在这里我们也可以透过学习来预测每年度，甚至每个月中哪一个CINA会产生故障的机率，以大幅降低停电时间和停电频率，甚至有效地消除区域性大停电。当然在学习过程中，我们可以知道那些CINA所需的电力线段容量需要加以提高，并且依据电力干线的输入与接收量可以改善网损的状况。在高级配电自动化系统中的技术也包括了系统拓朴、通信架构和信息模型开发、智能监视、与智能配电控制。本文也提供一电力需求预测模型以提供各INA需求预测，此模型也可以用作停电时间与停电频率的预测。由本文提出的各项技术，相信对智能电网能提供最佳的服务与技术解决方案。