垂心四面体的勾股4态15个外接球半径、外心坐标及距离的算法——四维体积勾股定理的应用(公式九)

Calculation of Radius, Circumcenter Coordinates and Distance of 15 Circumscribed Spheres of Pythagorean 4-State in an Orthocentric Tetrahedron—Application of Pythagorean Theorem of Four-Dimensional Volume (Formula 9)

摘要: 用正交4球半径的4元数，证明：垂心四面体的勾股4态的15个外接球半径同构公式、外心坐标同构公式；及其用外接球半径计算外心距离公式；以及12组棱角、6组面角，它们的互补对角的正弦余弦的代数值公式。

Abstract: By using the quaternions of orthogonal 4-sphere radius, it is proved that there are 15 isomorphic formulas of circumscribed sphere radius and circumcenter coordinate isomorphism of the Py-thagorean 4-state of the orthocentric tetrahedron, and the formula of calculating the distance of the circumcenter by using the radius of circumscribed sphere, as well as 12 sets of angles, 6 sets of face angles, their complementary diagonal sine and cosine of the numerical formula.

1. 引言

正交4球半径为4元数 [1]，其球心间勾股4态 [2] 的垂心四面体，已知有同构的重心球 [3] 和垂心球 [4] 半径及其它们的球心坐标和间距公式。那么正交4球的球心间的勾股4态的外接球 [5] 是否也有同构的半径公式及其球心坐标和间距公式？它们间的边角关系如何？

2. 证明正交4球 [1] 球心间勾股4态 [2] 的15个外接球 [5] 半径及其外心坐标同构公式

设：沿用文 [3] 即：正交4球心为大写： $A,B,C,D$ ：及相对应的球半径为小写： $a,b,c,d$ ；

$\left(A\in a;B\in b;C\in c;D\in d\right)$

正交4球心坐标为： $A\left(a,0,0\right);B\left(0,b,0\right);C\left(0,0,c\right);D\left(bct,act,abt\right)$

(这里： $t=\frac{-d^2}{v+abc}$, $v=\sqrt{a^2{b}^2{c}^2+a^2{b}^2{d}^2+a^2{c}^2{d}^2+b^2{c}^2{d}^2}=6V_{ABCD}$ ；D坐标在第7象限)

2.1. 一至四维球心间同构的外接球半径平方公式

定义：一至四维球心间外接球半径的平方：等于同态维数与重心球半径 [3] 之积方与同态维数减2与垂心球半径 [4] 的积方之差的四分之一。其公式为：

${\left({ℝ}_{Oi}^n\right)}^2=\frac{1}{4}\left[n^2{R}_{Gi}^2-{\left(n-2\right)}^2{r}_{Hi}^2\right]$ (1)

这里：字母为各类球半径： $ℝ$ 为外接球；R为重心球；r为垂心球；

下标：同态用 $i=A,B,C,D,\cdots$ ；O为外接球；G为重心球；H为垂心球；

右式上标与左式的 $n=1,2,3,4,\cdots$ 为勾股4态的1至4维。

· 4个一维外接球半径的平方：

${\left({ℝ}_{OA}^1\right)}^2=\frac{1}{4}\left[1^2{a}^2-{\left(1-2\right)}^2{a}^2\right]=\frac{1}{4}{1}^2\left(a^2-a^2\right)+\left(1-1\right)a^2=0$

因一维重心球半径与垂心球半径等同为4个正交球半径，4个一维外接球半径平方均为0，

即： ${\left({ℝ}_{OA}^1\right)}^2={\left({ℝ}_{OB}^1\right)}^2={\left({ℝ}_{OC}^1\right)}^2={\left({ℝ}_{OD}^1\right)}^2=0$。

· 6个二维外接球半径的平方：

${\left({ℝ}_{OAB}^2\right)}^2=\frac{1}{4}\left[2^2\times \frac{1}{2^2}\left(a^2+b^2\right)-{\left(2-2\right)}^2\frac{a^2{b}^2}{a^2+b^2}\right]=\frac{1}{4}\left(a^2+b^2\right)$

6个二维外接球半径与二维重心球半径相同，其平方为：

$\frac{a^2+b^2}{4},\frac{a^2+c^2}{4},\frac{a^2+d^2}{4},\frac{b^2+c^2}{4},\frac{b^2+d^2}{4},\frac{c^2+d^2}{4}$

因此证明其半径的平方可参见文 [3]。

· 4个三维外接球半径的平方：

${\left({ℝ}_{OABC}^3\right)}^2=\frac{1}{4}\left[3^2\times \frac{1}{3^2}\left(a^2+b^2+c^2\right)-{\left(3-2\right)}^2\frac{a^2{b}^2{c}^2}{s_{ABC}^2}\right]=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}$

4个三维外接球半径的平方：

$\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}$, $\frac{\left(a^2+b^2\right)\left(a^2+d^2\right)\left(b^2+d^2\right)}{4s_{ABD}^2}$,

$\frac{\left(a^2+c^2\right)\left(a^2+d^2\right)\left(c^2+d^2\right)}{4s_{ACD}^2}$, $\frac{\left(b^2+c^2\right)\left(b^2+d^2\right)\left(c^2+d^2\right)}{4s_{BCD}^2}$,

这里： $s_{ABC}^2=a^2{b}^2+a^2{c}^2+b^2{c}^2$， $s_{ABD}^2=a^2{b}^2+a^2{d}^2+b^2{d}^2$， $s_{ACD}^2=a^2{c}^2+a^2{d}^2+c^2{d}^2$， $s_{BCD}^2=b^2{c}^2+b^2{d}^2+c^2{d}^2$ (下同)。

其证明略：因其与三角形的外接圆公式等价。

· 1个四维外接球半径的平方：

${\left({ℝ}_O^4\right)}^2=\frac{1}{4}\left[4^2\times \frac{1}{4^2}\left(a^2+b^2+c^2+d^2\right)-{\left(4-2\right)}^2\frac{a^2{b}^2{c}^2{d}^2}{v^2}\right]=\frac{1}{4}\left(a^2+b^2+c^2+d^2-\frac{4a^2{b}^2{c}^2{d}^2}{v^2}\right)$

这里： $v^2=a^2{b}^2{c}^2+a^2{b}^2{d}^2+a^2{c}^2{d}^2+b^2{c}^2{d}^2$ (下同)。

其证明：见文 [5] 关于一维点态8点共球半径。即：正交4球心构成垂心四面体的外接球的半径。

2.2. 一至四维球心间同构的外心坐标同构公式

定义：一至四维15点外心坐标公式：三个分坐标均为维数 [2] 与同态重心分坐标 [3] 积减维数 [2] 减2与同态垂心分坐标 [4] 之积的差的二分之一。其公式为：

${\mathbb{O}}_i^n=\{\begin{array}{l}{x}_{Oi}=\frac{1}{2}\left[n{x}_{Gi}-\left(n-2\right)x_{Hi}\right]\\ y_{Oi}=\frac{1}{2}\left[n{y}_{Gi}-\left(n-2\right)y_{Hi}\right]\\ z_{Oi}=\frac{1}{2}\left[n{z}_{Gi}-\left(n-2\right)z_{Hi}\right]\end{array}$ (2)

这里字母： $\mathbb{O}$ 为外心坐标；x, y, z为分坐标；

下标：同态为 $i=A,B,C,D,\cdots$ ；Oi为外心坐标；Gi为垂心坐标；Hi为垂心坐标；

右式上标与左式 $n=1,2,3,4,\cdots$ 为勾股4态 [2] 的1至4维；

例：

· 4个一维点即正交1球心的外心坐标：

${\mathbb{O}}_A^1=\{\begin{array}{l}{x}_{OA}=\frac{1}{2}\left[1\times a-\left(1-2\right)a\right]=\frac{1}{2}\times 1\left(a-a\right)+a=a\\ y_{OA}=\frac{1}{2}\left[1\times 0-\left(1-2\right)0\right]=\frac{1}{2}\times 1\left(0-0\right)+0=0\\ z_{OA}=\frac{1}{2}\left[1\times 0-\left(1-2\right)0\right]=\frac{1}{2}\times 1\left(0-0\right)+0=0\end{array}$

一维外心坐标与正交4球球心坐标共点，同时也与一维重心和垂心坐标共点。

即： ${\mathbb{O}}_A^1\left(a,0,0\right),{\mathbb{O}}_B^1\left(0,b,0\right),{\mathbb{O}}_C^1\left(0,0,c\right),{\mathbb{O}}_D^1\left(bct,act,abt\right)$。

· 6个二维棱即正交2球心连线构成棱的外心坐标：

${\mathbb{O}}_{AB}^2=\{\begin{array}{l}{x}_{OAB}=\frac{1}{2}\left[2\times \frac{a+0}{2}-\left(2-2\right)\frac{a{b}^2}{a^2+b^2}\right]=\frac{1}{2}\times 2\left(\frac{a+0}{2}-\frac{a{b}^2}{a^2+b^2}\right)+\frac{a{b}^2}{a^2+b^2}=\frac{a}{2}\\ y_{OAB}=\frac{1}{2}\left[2\times \frac{0+b}{2}-\left(2-2\right)\frac{a^{2}b}{a^2+b^2}\right]=\frac{1}{2}\times 2\left(\frac{0+b}{2}-\frac{a^{2}b}{a^2+b^2}\right)+\frac{a^{2}b}{a^2+b^2}=\frac{b}{2}\\ z_{OAB}=\frac{1}{2}\left[2\times \frac{0+0}{2}-\left(2-2\right)0\right]=\frac{1}{2}\times 2\left(\frac{0+0}{2}-0\right)+0=0\end{array}$

同理：6个二维外心坐标与同态二维重心坐标共点为：

$\begin{array}{l}{\mathbb{O}}_{AB}^2\left(\frac{a}{2},\frac{b}{2},0\right);{\mathbb{O}}_{AC}^2\left(0,\frac{b}{2},\frac{c}{2}\right);{\mathbb{O}}_{BC}^2\left(0,\frac{b}{2},\frac{c}{2}\right);\\ {\mathbb{O}}_{AD}^2\left(\frac{a+bct}{2},\frac{act}{2},\frac{abt}{2}\right);{\mathbb{O}}_{BD}^2\left(\frac{bct}{2},\frac{b+act}{2},\frac{abt}{2}\right);{\mathbb{O}}_{CD}^2\left(\frac{bct}{2},\frac{act}{2},\frac{c+abt}{2}\right)\end{array}$

其半径平方与二维重心球半径平方共球。其二维外心与二维重心共点，坐标验证见文 [3]。

· 4个三维面即正交3球心构成三角形的外心坐标：

${\mathbb{O}}_{ABC}^3=\{\begin{array}{l}{x}_{OABC}=\frac{1}{2}\left[3\times \frac{a+0+0}{3}-\left(3-2\right)\frac{a{b}^2{c}^2}{s_{ABC}^2}\right]=\frac{1}{2}\left(a-\frac{a{b}^2{c}^2}{s_{ABC}^2}\right)=\frac{a^3\left(b^2+c^2\right)}{2s_{ABC}^2}\\ y_{OABC}=\frac{1}{2}\left[3\times \frac{0+b+0}{3}-\left(3-2\right)\frac{a^{2}b{c}^2}{s_{ABC}^2}\right]=\frac{1}{2}\left(b-\frac{a^{2}b{c}^2}{s_{ABC}^2}\right)=\frac{b^3\left(a^2+c^2\right)}{2s_{ABC}^2}\\ z_{OABC}=\frac{1}{2}\left[3\times \frac{0+0+c}{3}-\left(3-2\right)\frac{a^2{b}^{2}c}{s_{ABC}^2}\right]=\frac{1}{2}\left(c-\frac{a^2{b}^{2}c}{s_{ABC}^2}\right)=\frac{c^3\left(a^2+b^2\right)}{2s_{ABC}^2}\end{array}$

4个三维面外心坐标为：

${\mathbb{O}}_{ABC}^3\left(\frac{a^3\left(b^2+c^2\right)}{2s_{ABC}^2},\frac{b^3\left(a^2+c^2\right)}{2s_{ABC}^2},\frac{c^3\left(a^2+b^2\right)}{2s_{ABC}^2}\right)$ ；

${\mathbb{O}}_{ABD}^3\left(\frac{a{b}^{2}tv+\left(a+bct\right)s_{ABD}^2}{2s_{ABD}^2},\frac{a^{2}btv+\left(b+act\right)s_{ABD}^2}{2s_{ABD}^2},\frac{ab\left(a^2+b^2\right)d^{2}t}{2s_{ABD}^2}\right)$ ；

${\mathbb{O}}_{ACD}^3\left(\frac{a{c}^{2}tv+\left(a+bct\right)s_{ACD}^2}{2s_{ACD}^2},\frac{ac\left(a^2+c^2\right)d^{2}t}{2s_{ACD}^2},\frac{a^{2}ctv+\left(c+abt\right)s_{ACD}^2}{2s_{ACD}^2}\right)$ ；

${\mathbb{O}}_{BCD}^3\left(\frac{bc\left(b^2+c^2\right)d^{2}t}{2s_{BCD}^2},\frac{b{c}^{2}tv+\left(b+act\right)s_{BCD}^2}{2s_{BCD}^2},\frac{b^{2}ctv+\left(c+abt\right)s_{BCD}^2}{2s_{BCD}^2}\right)$

这里： $s_{ABC}^2=a^2{b}^2+a^2{c}^2+b^2{c}^2$， $s_{ABD}^2=a^2{b}^2+a^2{d}^2+b^2{d}^2$，

$s_{ACD}^2=a^2{c}^2+a^2{d}^2+c^2{d}^2$， $s_{BCD}^2=b^2{c}^2+b^2{d}^2+c^2{d}^2$ (下同)。

验证：用2点坐标距离公式验证该点为3维外心：

例：三维外心 ${\mathbb{O}}_{ABC}^3$ 与共面的3个正交球球心A、B、C，分别用2点式间距公式计算，结果相同：

${\left|A{\mathbb{O}}_{ABC}^3\right|}^2={\left[\frac{a^3\left(b^2+c^2\right)}{2s_{ABC}^2}-a\right]}^2+{\left[\frac{b^3\left(a^2+c^2\right)}{2s_{ABC}^2}-0\right]}^2+{\left[\frac{c^3\left(a^2+b^2\right)}{2s_{ABC}^2}-0\right]}^2=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}$

${\left|B{\mathbb{O}}_{ABC}^3\right|}^2={\left[\frac{a^3\left(b^2+c^2\right)}{2s_{ABC}^2}-0\right]}^2+{\left[\frac{b^3\left(a^2+c^2\right)}{2s_{ABC}^2}-b\right]}^2+{\left[\frac{c^3\left(a^2+b^2\right)}{2s_{ABC}^2}-0\right]}^2=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}$

${\left|C{\mathbb{O}}_{ABC}^3\right|}^2={\left[\frac{a^3\left(b^2+c^2\right)}{2s_{ABC}^2}-0\right]}^2+{\left[\frac{b^3\left(a^2+c^2\right)}{2s_{ABC}^2}-0\right]}^2+{\left[\frac{c^3\left(a^2+b^2\right)}{2s_{ABC}^2}-c\right]}^2=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}$

同理：可验证其余3组均为其3维外心。

· 1个四维体即正交4球心构成垂心四面体的外心坐标：

${\mathbb{O}}^4=\{\begin{array}{l}{x}_O=\frac{1}{2}\left[4\times \frac{a+bct}{4}-\left(4-2\right)\frac{-a{b}^2{c}^{2}t}{v}\right]=\frac{1}{2}\left(a+bct+\frac{2a{b}^2{c}^{2}t}{v}\right)=\frac{av+bct\left(2abc+v\right)}{2v}\\ y_O=\frac{1}{2}\left[4\times \frac{b+act}{4}-\left(4-2\right)\frac{-a^{2}b{c}^{2}t}{v}\right]=\frac{1}{2}\left(b+act+\frac{2a^{2}b{c}^{2}t}{v}\right)=\frac{bv+act\left(2abc+v\right)}{2v}\\ z_O=\frac{1}{2}\left[4\times \frac{c+abt}{4}-\left(4-2\right)\frac{-a^2{b}^{2}ct}{v}\right]=\frac{1}{2}\left(c+abt+\frac{2a^2{b}^{2}ct}{v}\right)=\frac{cv+abt\left(2abc+v\right)}{2v}\end{array}$

这里： $t=\frac{-d^2}{abc+v}$ ； $v^2=a^2{b}^2{c}^2+a^2{b}^2{d}^2+a^2{c}^2{d}^2+b^2{c}^2{d}^2$ (下同)。

验证该4维外心：见文 [5]。

2.3. 一至四维及其幂集的任意子集外心间距的同构公式

定义：一至四维及其幂集的任意子集外心间距同构公式为：其外心间距的平方等于外接球半径与其幂集的任意一个非空子集的外接球半径的平方差。其公式为：

${\mathbb{D}}_{A|Ai\in A}^2={\left|{ℝ}_A^n\right|}^2-{\left|{ℝ}_{Ai}^{ni}\right|}^2$ (3)

这里： $\mathbb{D}$ 为间距， $ℝ$ 为外接球半径(详见：表1)；

上标：n为勾股4态 [2] 的1至4维维数，ni为其幂集子集的维数；

下标：A为集，Ai为A集的幂集的任意一项非空子集。

例：

· 4组一维点外心的每组非零幂集数为：已知非零幂集数量公式为： $x=2^n-1$。则一维非空幂集数为： $2^1-1=1$ (1点与集共点)。对于A球外心自身间距套用公式后为：

${\mathbb{D}}_{A|A}^2={\left|{ℝ}_{OA}^1\right|}^2-{\left|{ℝ}_{OA}^1\right|}^2=0-0=0$

同理：其余3个一维点外心自身间距均为零。

· 6组二维棱外心的每组非零幂集数为 $2^2-1=3$ (3点与集共棱)。即：

${\mathbb{D}}_{AB|AB}^2={\left|{ℝ}_{OAB}^2\right|}^2-{\left|{ℝ}_{OAB}^2\right|}^2=\frac{1}{2^2}\left(a^2+b^2\right)-\frac{1}{2^2}\left(a^2+b^2\right)=0$

${\mathbb{D}}_{AB|A}^2={\left|{ℝ}_{OAB}^2\right|}^2-{\left|{ℝ}_{OA}^1\right|}^2=\frac{1}{2^2}\left(a^2+b^2\right)-0=\frac{1}{2^2}\left(a^2+b^2\right)$

${\mathbb{D}}_{AB|B}^2={\left|{ℝ}_{OAB}^2\right|}^2-{\left|{ℝ}_{OB}^1\right|}^2=\frac{1}{2^2}\left(a^2+b^2\right)-0=\frac{1}{2^2}\left(a^2+b^2\right)$

同理：可得其余5组，每组二维外接球球心与其非零幂集各3个子集外心间距(略)；

验证：因二维棱外心坐标及其半径与二维重心坐标及其半径等价。其验证见文 [3]。

· 4组三维面外心的每组非零幂集数为 $2^3-1=7$ (7点与集共面)。即：

${\mathbb{D}}_{ABC|ABC}^2={\left|{ℝ}_{OABC}^3\right|}^2-{\left|{ℝ}_{OABC}^3\right|}^2=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}-\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}=0$

${\mathbb{D}}_{ABC|AB}^2={\left|{ℝ}_{OABC}^3\right|}^2-{\left|{ℝ}_{OAB}^2\right|}^2=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}-\frac{1}{2^2}\left(a^2+b^2\right)=\frac{\left(a^2+b^2\right)c^4}{4s_{ABC}^2}$

${\mathbb{D}}_{ABC|AC}^2={\left|{ℝ}_{OABC}^3\right|}^2-{\left|{ℝ}_{OAC}^2\right|}^2=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}-\frac{1}{2^2}\left(a^2+c^2\right)=\frac{\left(a^2+c^2\right)b^4}{4s_{ABC}^2}$

${\mathbb{D}}_{ABC|BC}^2={\left|{ℝ}_{OABC}^3\right|}^2-{\left|{ℝ}_{OBC}^2\right|}^2=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}-\frac{1}{2^2}\left(b^2+c^2\right)=\frac{\left(b^2+c^2\right)a^4}{4s_{ABC}^2}$

${\mathbb{D}}_{ABC|A}^2={\left|{ℝ}_{OABC}^3\right|}^2-{\left|{ℝ}_{OA}^1\right|}^2=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}-0=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}$

${\mathbb{D}}_{ABC|B}^2={\left|{ℝ}_{OABC}^3\right|}^2-{\left|{ℝ}_{OB}^1\right|}^2=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}-0=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}$

${\mathbb{D}}_{ABC|C}^2={\left|{ℝ}_{OABC}^3\right|}^2-{\left|{ℝ}_{OC}^1\right|}^2=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}-0=\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}$

同理可得其余3组3维面外心与其非零幂集各7个子集外心间距。

每组与7个子集外心间距关系，可分3类，可分别验证2点间外接球半径的平方差：

一类：自身间距为零；

二类：根据三角形外心到各边的垂线平分各边的定理，符合直角三角形斜边与底边的平方差等于邻边平方；

三类：根据三角形外心到各顶点的间距相等为3维外接球半径。

· 1组四维体外心的非零幂集数为 $2^4-1=15$ (15点与集共体)。即：

${\mathbb{D}}_{O|O}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_O^4\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}=0$

${\mathbb{D}}_{O|ABC}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OABC}^3\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}=\frac{{\left(2a^2{b}^2{c}^2-v^2\right)}^2}{4s_{ABC}^2{v}^2}$

${\mathbb{D}}_{O|ABD}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OABD}^3\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-\frac{\left(a^2+b^2\right)\left(a^2+d^2\right)\left(b^2+d^2\right)}{4s_{ABD}^2}=\frac{{\left(2a^2{b}^2{d}^2-v^2\right)}^2}{4s_{ABD}^2{v}^2}$

${\mathbb{D}}_{O|ACD}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OACD}^3\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-\frac{\left(a^2+b^2\right)\left(a^2+d^2\right)\left(b^2+d^2\right)}{4s_{ACD}^2}=\frac{{\left(2a^2{c}^2{d}^2-v^2\right)}^2}{4s_{ACD}^2{v}^2}$

${\mathbb{D}}_{O|BCD}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OBCD}^3\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-\frac{\left(a^2+b^2\right)\left(a^2+d^2\right)\left(b^2+d^2\right)}{4s_{BCD}^2}=\frac{{\left(2b^2{c}^2{d}^2-v^2\right)}^2}{4s_{BCD}^2{v}^2}$

${\mathbb{D}}_{O|AB}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OAB}^2\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-\frac{1}{2^2}\left(a^2+b^2\right)=\frac{\left(c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}$

${\mathbb{D}}_{O|AC}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OAC}^2\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-\frac{1}{2^2}\left(a^2+c^2\right)=\frac{\left(b^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}$

${\mathbb{D}}_{O|AD}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OAD}^2\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-\frac{1}{2^2}\left(a^2+d^2\right)=\frac{\left(b^2+c^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}$

${\mathbb{D}}_{O|BC}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OBC}^2\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-\frac{1}{2^2}\left(b^2+c^2\right)=\frac{\left(a^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}$

${\mathbb{D}}_{O|BD}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OBD}^2\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-\frac{1}{2^2}\left(b^2+d^2\right)=\frac{\left(a^2+c^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}$

${\mathbb{D}}_{O|CD}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OCD}^2\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-\frac{1}{2^2}\left(c^2+d^2\right)=\frac{\left(a^2+b^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}$

${\mathbb{D}}_{O|A}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OA}^1\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-0=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}$

${\mathbb{D}}_{O|B}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OB}^1\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-0=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}$

${\mathbb{D}}_{O|C}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OC}^1\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-0=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}$

${\mathbb{D}}_{O|D}^2={\left|{ℝ}_O^4\right|}^2-{\left|{ℝ}_{OD}^1\right|}^2=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}-0=\frac{\left(a^2+b^2+c^2+d^2\right)v^2-4a^2{b}^2{c}^2{d}^2}{4v^2}$

上述4维外接球切四面、6棱、4点形成曲率等价。即：

垂心四面体外心到各面的垂线为各面的外心、到各棱的垂线平分各棱的外心、到各正交球心的各点的外心。它们的间距均4维外接球半径与其任一子集外接球半径的平方差。

根据：所设以及公式(1)、公式(2)计算的结果作(表1)如下：并为方便观察作(图1)。

2.4. 所设一至四维各外心坐标及其半径(见表1)，各坐标位置(见图1)

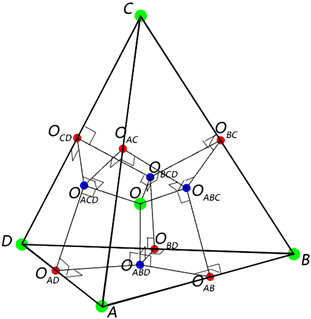
Figure 1. Schematic diagram of 1~4-d 15 point circumcenter coordinates

图1. 1至4维15点外心坐标示意图

Table 1. The square of radius of 15 circumscribed spheres in Pythagorean 4-state and the symbol of circumcenter coordinates

表1. 勾股4态15个外接球半径的平方及其外心坐标符号

表内：字母：a, b, c, d为正交四球的4个半径；

D坐标在第7象限。 $t=\frac{-d^2}{v+abc}$ ； $v=\sqrt{a^2{b}^2{c}^2+a^2{b}^2{d}^2+a^2{c}^2{d}^2+b^2{c}^2{d}^2}=6V_{ABCD}$ ； $s_{ABC}^2=a^2{b}^2+a^2{c}^2+b^2{c}^2$ ； $s_{ABD}^2=a^2{b}^2+a^2{d}^2+b^2{d}^2$ ； $s_{ACD}^2=a^2{c}^2+a^2{d}^2+c^2{d}^2$ ； $s_{BCD}^2=b^2{c}^2+b^2{d}^2+c^2{d}^2$。

2.5. 图1中含有18组4点所围的4边形：均共面、共圆、对角互补符合托勒密定理

上述18组可分两类其中：

2.5.1. 计算证明维数1 (2、2) 3间连线的为：3组/面 × 4面 = 12组

证明A、B、C、O_AB、O_AC、O_BC、O_ABC七点所围的3组四边形，每组有一对角互补均为90度，另一组对角线等长为3维外心至3顶点为外接球半径。因此用托勒密定理：圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。可得3维外心至3顶点为外接球半径的一组方程为：

$\sqrt{\frac{\left(a^2+c^2\right)\left(a^2+b^2\right)\left(b^2+c^2\right)}{4s_{ABC}^2}}=\{\begin{array}{l}\left|A{O}_{ABC}\right|=\frac{\left|O_{AC}{O}_{ABC}\right|\left|A{O}_{AB}\right|+\left|O_{AB}{O}_{ABC}\right|\left|A{O}_{AC}\right|}{\left|O_{AB}{O}_{AC}\right|}\\ \left|B{O}_{ABC}\right|=\frac{\left|O_{BC}{O}_{ABC}\right|\left|B{O}_{AB}\right|+\left|O_{AB}{O}_{ABC}\right|\left|B{O}_{BC}\right|}{\left|O_{AB}{O}_{BC}\right|}\\ \left|C{O}_{ABC}\right|=\frac{\left|O_{BC}{O}_{ABC}\right|\left|C{O}_{AC}\right|+\left|O_{AC}{O}_{ABC}\right|\left|C{O}_{BC}\right|}{\left|O_{AC}{O}_{BC}\right|}\end{array}$ (4)

同理：其余三面可得其余3维外心至3顶点为外接球半径的三组方程为：

$\sqrt{\frac{\left(a^2+b^2\right)\left(a^2+d^2\right)\left(b^2+d^2\right)}{4s_{ABD}^2}}=\{\begin{array}{l}\left|A{O}_{ABD}\right|=\frac{\left|O_{AD}{O}_{ABD}\right|\left|A{O}_{AB}\right|+\left|O_{AB}{O}_{ABD}\right|\left|A{O}_{AD}\right|}{\left|O_{AB}{O}_{AD}\right|}\\ \left|B{O}_{ABD}\right|=\frac{\left|O_{BD}{O}_{ABD}\right|\left|B{O}_{AB}\right|+\left|O_{AB}{O}_{ABD}\right|\left|B{O}_{BD}\right|}{\left|O_{AB}{O}_{BD}\right|}\\ \left|D{O}_{ABD}\right|=\frac{\left|O_{BD}{O}_{ABD}\right|\left|D{O}_{AD}\right|+\left|O_{AD}{O}_{ABD}\right|\left|D{O}_{BD}\right|}{\left|O_{AD}{O}_{BD}\right|}\end{array}$ (5)

$\sqrt{\frac{\left(a^2+c^2\right)\left(a^2+d^2\right)\left(c^2+d^2\right)}{4s_{ACD}^2}}=\{\begin{array}{l}\left|A{O}_{ACD}\right|=\frac{\left|O_{AC}{O}_{ACD}\right|\left|A{O}_{AD}\right|+\left|O_{AD}{O}_{ACD}\right|\left|A{O}_{AC}\right|}{\left|O_{AD}{O}_{AC}\right|}\\ \left|C{O}_{ACD}\right|=\frac{\left|O_{CD}{O}_{ACD}\right|\left|C{O}_{AC}\right|+\left|O_{AC}{O}_{ACD}\right|\left|C{O}_{CD}\right|}{\left|O_{AC}{O}_{CD}\right|}\\ \left|D{O}_{ACD}\right|=\frac{\left|O_{CD}{O}_{ACD}\right|\left|D{O}_{AD}\right|+\left|O_{AD}{O}_{ACD}\right|\left|D{O}_{CD}\right|}{\left|O_{AD}{O}_{CD}\right|}\end{array}$ (6)

$\sqrt{\frac{\left(b^2+c^2\right)\left(b^2+d^2\right)\left(c^2+d^2\right)}{4s_{BCD}^2}}=\{\begin{array}{l}\left|B{O}_{BCD}\right|=\frac{\left|O_{BC}{O}_{BCD}\right|\left|B{O}_{BD}\right|+\left|O_{BD}{O}_{BCD}\right|\left|B{O}_{BC}\right|}{\left|O_{BD}{O}_{BC}\right|}\\ \left|C{O}_{BCD}\right|=\frac{\left|O_{CD}{O}_{BCD}\right|\left|C{O}_{BC}\right|+\left|O_{BC}{O}_{BCD}\right|\left|C{O}_{CD}\right|}{\left|O_{BC}{O}_{CD}\right|}\\ \left|D{O}_{BCD}\right|=\frac{\left|O_{CD}{O}_{BCD}\right|\left|D{O}_{BD}\right|+\left|O_{BD}{O}_{BCD}\right|\left|D{O}_{CD}\right|}{\left|O_{BD}{O}_{CD}\right|}\end{array}$ (7)

上述右侧：分子内2点间距，均可用公式(3)求得，分母因与重心球等价，其重心间距均可用文 [3] 的距离公式求得，也可用2点坐标的距离公式计算。(展开略)

上述12组四边形，每组有一对角互补均为90度，4点共面共圆，符合对角互补的托勒密定理：

而其中12个棱角均为已知角，其正弦、余弦的代数值见文 [6]，其3维外心为顶点的角与对棱角为互补角，即π减对棱角即可。因此3维外心为顶点的对角的正弦等于棱角正弦、其余弦等于负棱角余弦。

所设：12个棱角的正弦、余弦代数值符号所设沿用文 [6]，它们12个对角均交于4个3维外心，分别所设：

例：A点对平面为1面，以3维外心O_BCD为顶点的3钝角为O_1B、O_1C、O_1D依次与对角B₁、C₁、D₁ 3棱角互补。

· 交于1面的3个棱角B₁、C₁、D₁依次互补对角为O_1B、O_1C、O_1D它们的正弦、余弦为：

见文 [6] 已知： $B_1=\angle CBD$， $\Rightarrow \cos B_1=\frac{b^2}{\left|BC\right|\left|BD\right|}$， $\Rightarrow \sin B_1=\frac{s_1}{\left|BC\right|\left|BD\right|}$ ；

其互补对角： $O_{1B}=\angle O_{BC}{O}_{BCD}{O}_{BD}=\pi -B_1$

$\Rightarrow \cos O_{1B}=\cos \left(\pi -B_1\right)=-\cos B_1=\frac{-b^2}{\left|BC\right|\left|BD\right|}$，

$\Rightarrow \sin O_{1B}=\sin \left(\pi -B_1\right)=\sin B_1=\frac{s_1}{\left|BC\right|\left|BD\right|}$ ；

见文 [6] 已知： $C_1=\angle BCD$， $\Rightarrow \cos C_1=\frac{c^2}{\left|BC\right|\left|CD\right|}$， $\Rightarrow \sin C_1=\frac{s_1}{\left|BC\right|\left|CD\right|}$ ；

其互补对角： $O_{1C}=\angle O_{BC}{O}_{BCD}{O}_{CD}=\pi -C_1$

$\Rightarrow \cos O_{1C}=\cos \left(\pi -C_1\right)=-\cos C_1=\frac{-c^2}{\left|BC\right|\left|CD\right|}$，

$\Rightarrow \sin O_{1C}=\sin \left(\pi -C_1\right)=\sin C_1=\frac{s_1}{\left|BC\right|\left|CD\right|}$ ；

见文 [6] 已知： $D_1=\angle BDC$， $\Rightarrow \cos D_1=\frac{d^2}{\left|BD\right|\left|CD\right|}$， $\Rightarrow \sin D_1=\frac{s_1}{\left|BD\right|\left|CD\right|}$ ；

其互补对角： $O_{1D}=\angle O_{BD}{O}_{BCD}{O}_{CD}=\pi -D_1$

$\Rightarrow \cos O_{1D}=\cos \left(\pi -D_1\right)=-\cos D_1=\frac{-d^2}{\left|BD\right|\left|CD\right|}$，

$\Rightarrow \sin O_{1D}=\sin \left(\pi -D_1\right)=\sin D_1=\frac{s_1}{\left|BD\right|\left|CD\right|}$ ；

同理：根据其它3面如下9个棱角的正弦和余弦，可方便得出其棱角的互补对角的正弦和余弦。

· 交于2面的3个棱角及其互补对角的正弦、余弦为：

见文 [6] 已知： $A_2=\angle CAD$， $\Rightarrow \cos A_2=\frac{a^2}{\left|AC\right|\left|AD\right|}$， $\Rightarrow \sin A_2=\frac{s_2}{\left|AC\right|\left|AD\right|}$ ；

其互补对角： $O_{2A}=\angle O_{AC}{O}_{ACD}{O}_{AD}=\pi -A_2$

$\Rightarrow \cos O_{2A}=-\cos A_2=\frac{-a^2}{\left|AC\right|\left|AD\right|}$， $\Rightarrow \sin O_{2A}=\sin A_2=\frac{s_2}{\left|AC\right|\left|AD\right|}$ ；

见文 [6] 已知： $C_2=\angle ACD$， $\Rightarrow \cos C_2=\frac{c^2}{\left|AC\right|\left|CD\right|}$， $\Rightarrow \sin C_2=\frac{s_2}{\left|AC\right|\left|CD\right|}$ ；

其互补对角： $O_{2C}=\angle O_{AC}{O}_{ACD}{O}_{CD}=\pi -C_2$

$\Rightarrow \cos O_{2C}=-\cos C_2=\frac{-c^2}{\left|AC\right|\left|CD\right|}$， $\Rightarrow \sin O_{2C}=\sin C_2=\frac{s_2}{\left|AC\right|\left|CD\right|}$ ；

见文 [6] 已知： $D_2=\angle ADC$， $\Rightarrow \cos D_2=\frac{d^2}{\left|AD\right|\left|CD\right|}$， $\Rightarrow \sin D_2=\frac{s_2}{\left|AD\right|\left|CD\right|}$ ；

其互补对角： $O_{2D}=\angle O_{AD}{O}_{ACD}{O}_{CD}=\pi -D_2$

$\Rightarrow \cos O_{2D}=-\cos D_2=\frac{-d^2}{\left|AD\right|\left|CD\right|}$， $\Rightarrow \sin O_{2D}=\sin D_2=\frac{s_2}{\left|AD\right|\left|CD\right|}$ ；

· 交于3面的3个棱角及其互补对角的正弦、余弦为：

见文 [6] 已知： $A_3=\angle BAD$， $\Rightarrow \cos A_3=\frac{a^2}{\left|AB\right|\left|AD\right|}$， $\Rightarrow \sin A_3=\frac{s_3}{\left|AB\right|\left|AD\right|}$ ；

其互补对角： $O_{3A}=\angle O_{AD}{O}_{ABD}{O}_{BD}=\pi -A_3$

$\Rightarrow \cos O_{3A}=-\cos A_3=\frac{-a^2}{\left|AB\right|\left|AD\right|}$， $\Rightarrow \sin O_{3A}=\sin A_3=\frac{s_3}{\left|AB\right|\left|AD\right|}$ ；

见文 [6] 已知： $B_3=\angle ABD$， $\Rightarrow \cos B_3=\frac{b^2}{\left|AB\right|\left|BD\right|}$， $\Rightarrow \sin B_3=\frac{s_3}{\left|AB\right|\left|BD\right|}$ ；

其互补对角： $O_{3B}=\angle O_{AB}{O}_{ABD}{O}_{BD}=\pi -B_3$

$\Rightarrow \cos O_{3B}=-\cos B_3=\frac{-b^2}{\left|AB\right|\left|BD\right|}$， $\Rightarrow \sin O_{3B}=\sin B_3=\frac{s_3}{\left|AB\right|\left|BD\right|}$ ；

见文 [6] 已知： $D_3=\angle ADB$， $\Rightarrow \cos D_3=\frac{d^2}{\left|AD\right|\left|BD\right|}$， $\Rightarrow \sin D_3=\frac{s_3}{\left|AD\right|\left|BD\right|}$ ；

其互补对角： $O_{3D}=\angle O_{AD}{O}_{ABD}{O}_{BD}=\pi -D_3$

$\Rightarrow \cos O_{3D}=-\cos D_3=\frac{-d^2}{\left|AD\right|\left|BD\right|}$， $\Rightarrow \sin O_{3D}=\sin D_3=\frac{s_3}{\left|AD\right|\left|BD\right|}$ ；

· 交于4面的3个棱角及其互补对角的正弦、余弦为：

见文 [6] 已知： $A_4=\angle BAC$ ； $\Rightarrow \cos A_4=\frac{a^2}{\left|AB\right|\left|AC\right|}$， $\Rightarrow \sin A_4=\frac{s_4}{\left|AB\right|\left|AC\right|}$ ；

其互补对角： $O_{4A}=\angle O_{AB}{O}_{ABC}{O}_{AC}=\pi -A_4$

$\Rightarrow \cos O_{4A}=-\cos A_4=\frac{-a^2}{\left|AB\right|\left|AC\right|}$， $\Rightarrow \sin O_{4A}=\sin A_4=\frac{s_4}{\left|AB\right|\left|AC\right|}$ ；

见文 [6] 已知： $B_4=\angle ABC$ ； $\Rightarrow \cos B_4=\frac{b^2}{\left|AB\right|\left|BC\right|}$， $\Rightarrow \sin B_4=\frac{s_4}{\left|AB\right|\left|BC\right|}$ ；

其互补对角： $O_{4B}=\angle O_{AB}{O}_{ABC}{O}_{BC}=\pi -B_4$

$\Rightarrow \cos O_{4B}=-\cos B_4=\frac{-b^2}{\left|AB\right|\left|BC\right|}$， $\Rightarrow \sin O_{4B}=\sin B_4=\frac{s_4}{\left|AB\right|\left|BC\right|}$ ；

见文 [6] 已知： $C_4=\angle ACB$ ； $\Rightarrow \cos C_4=\frac{c^2}{\left|AC\right|\left|CB\right|}$， $\Rightarrow \sin C_4=\frac{s_4}{\left|AC\right|\left|CB\right|}$ ；

其互补对角： $O_{4C}=\angle O_{AC}{O}_{ABC}{O}_{BC}=\pi -C_4$

$\Rightarrow \cos O_{4C}=-\cos C_4=\frac{-c^2}{\left|AC\right|\left|CB\right|}$， $\Rightarrow \sin O_{4C}=\sin C_4=\frac{s_4}{\left|AC\right|\left|CB\right|}$ ；

2.5.2. 计算证明维数2 (3、3) 4间连线的为：1组/棱 × 6棱 = 6组

证明：AB棱中点垂直的O_AB、O_ABC、O_ABD、O四点所围四边形，且4点共面共圆，其中以3维外心为顶点的对角均为90度，用托勒密定理：圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积，可得一组方程组：

$\left|O{O}_{AB}\right|\left|O_{ABC}{O}_{ABD}\right|=\left|O_{AB}{O}_{ABD}\right|\left|O{O}_{ABC}\right|+\left|O_{AB}{O}_{ABC}\right|\left|O{O}_{ABD}\right|$ (8)

同理可得其它5组托勒密定理的方程组：

$\left|O{O}_{AC}\right|\left|O_{ABC}{O}_{ACD}\right|=\left|O_{AC}{O}_{ABC}\right|\left|O{O}_{ACD}\right|+\left|O_{AC}{O}_{ACD}\right|\left|O{O}_{ABC}\right|$

$\left|O{O}_{AD}\right|\left|O_{ABD}{O}_{ACD}\right|=\left|O_{AD}{O}_{ABD}\right|\left|O{O}_{ACD}\right|+\left|O_{AD}{O}_{ACD}\right|\left|O{O}_{ABD}\right|$

$\left|O{O}_{BC}\right|\left|O_{ABC}{O}_{BCD}\right|=\left|O_{BC}{O}_{ABC}\right|\left|O{O}_{BCD}\right|+\left|O_{BC}{O}_{BCD}\right|\left|O{O}_{ABC}\right|$

$\left|O{O}_{BD}\right|\left|O_{ABD}{O}_{BCD}\right|=\left|O_{BD}{O}_{ABD}\right|\left|O{O}_{BCD}\right|+\left|O_{BD}{O}_{BCD}\right|\left|O{O}_{ABD}\right|$

$\left|O{O}_{CD}\right|\left|O_{ACD}{O}_{BCD}\right|=\left|O_{CD}{O}_{ACD}\right|\left|O{O}_{BCD}\right|+\left|O_{CD}{O}_{BCD}\right|\left|O{O}_{ACD}\right|$

上述右侧3维外心2点的距离需用坐标距离公式计算外，其余均可用公式(3)求得。(展开略)

通过公式(3)也证明了4维外心O与4个面的垂线为4面的3维外心O_ABC、O_ABD、O_ACD、O_BCD，因此上式6组四边形在以3维外心为顶点的对角均为90度，符合托勒密定理。

另一组互补对角，交于2维外心与3维外心连线的夹角与垂心四面体的两面角等价，它们的正弦、余弦的代数值均已知见文 [6]，它们交于CD、BD、BC、AD、AC、AB六棱的6个面角符号为 ${\alpha }_{12}$ 、 ${\alpha }_{13}$ 、 ${\alpha }_{14}$ 、 ${\alpha }_{23}$ 、 ${\alpha }_{24}$ 、 ${\alpha }_{34}$，与顶点交于4维外心O与3维外心垂直连线的6个互补对角依次符号为：O₁₂、O₁₃、O₁₄、O₂₃、O₂₄、O₃₄。因此，互补对角的正弦与面角相同，互补对角的余弦为面角余弦的负值。证明如下：

· 根据已知垂直交于CD棱的面角，解顶点位于O外心的互补对角的正弦、余弦代数值为：

证明：O、O_ACD、O_BCD、O_CD 4点共面：利用平面方程即：

$\begin{array}{l}0=\left|\begin{array}{ccc}x-x_1& y-y_1& z-z_1\\ x_2-x_1& y_2-y_1& z_2-z_1\\ x_3-x_1& y_3-y_1& z_3-z_1\end{array}\right|=\left|\begin{array}{ccc}{x}_O-x_{O_{CD}}& y_O-y_{O_{CD}}& z_O-z_{O_{CD}}\\ x_{O_{ACD}}-x_{O_{CD}}& y_{O_{ACD}}-y_{O_{CD}}& z_{O_{ACD}}-z_{O_{CD}}\\ x_{O_{BCD}}-x_{O_{CD}}& y_{O_{BCD}}-y_{O_{CD}}& z_{O_{BCD}}-z_{O_{CD}}\end{array}\right|\Rightarrow 代入坐标\\ =\left|\begin{array}{ccc}\frac{av+bct\left(2abc+v\right)}{2v}-\frac{bct}{2}& \frac{bv+act\left(2abc+v\right)}{2v}-\frac{act}{2}& \frac{cv+abt\left(2abc+v\right)}{2v}-\frac{c+abt}{2}\\ \frac{a{c}^{2}tv+\left(a+bct\right)s_{ACD}^2}{2s_{ACD}^2}-\frac{bct}{2}& \frac{ac\left(a^2+c^2\right)d^{2}t}{2s_{ACD}^2}-\frac{act}{2}& \frac{a^{2}ctv+\left(c+abt\right)s_{ACD}^2}{2s_{ACD}^2}-\frac{c+abt}{2}\\ \frac{bc\left(b^2+c^2\right)d^{2}t}{2s_{BCD}^2}-\frac{bct}{2}& \frac{b{c}^{2}tv+\left(b+act\right)s_{BCD}^2}{2s_{BCD}^2}-\frac{act}{2}& \frac{b^{2}ctv+\left(c+abt\right)s_{BCD}^2}{2s_{BCD}^2}-\frac{c+abt}{2}\end{array}\right|\\ =\frac{a^3{b}^{3}c{d}^2\left(c^2+d^2\right)\left(v^2-v^2\right)}{4v{s}_{ACD}^2{s}_{BCD}^2\left(abc+v\right)}=0\end{array}$

(同理可证其余5组与棱垂直的4点共面。)

见文 [6] 已知： ${\alpha }_{12}=\angle A{H}_{CD}B=\angle O_{ACD}{O}_{CD}{O}_{BCD}$， $\Rightarrow \cos {\alpha }_{12}=\frac{c^2{d}^2}{s_1{s}_2}$， $\Rightarrow \sin {\alpha }_{12}=\frac{\left|CD\right|v}{s_1{s}_2}$，

其互补对角： $O_{12}=\angle O_{ACD}O{O}_{BCD}=\pi -{\alpha }_{12}$

$\Rightarrow \cos O_{12}=\cos \left(\pi -{\alpha }_{12}\right)=-\cos {\alpha }_{12}=\frac{-c^2{d}^2}{s_1{s}_2}$ ； $\Rightarrow \sin O_{12}=\sin \left(\pi -{\alpha }_{12}\right)=\sin {\alpha }_{12}=\frac{\left|CD\right|v}{s_1{s}_2}$

· 根据已知垂直交于BD棱的面角，解顶点位于O外心的互补对角的正弦、余弦代数值为：

见文 [6] 已知： ${\alpha }_{13}=\angle A{H}_{BD}C=\angle O_{ABD}{O}_{BD}{O}_{BCD}$， $\Rightarrow \cos {\alpha }_{13}=\frac{b^2{d}^2}{s_1{s}_3}$， $\Rightarrow \sin {\alpha }_{13}=\frac{\left|BD\right|v}{s_1{s}_3}$ ；

其互补对角： $O_{13}=\angle O_{ABD}O{O}_{BCD}=\pi -{\alpha }_{13}$

$\Rightarrow \cos O_{13}=\cos \left(\pi -{\alpha }_{13}\right)=-\cos {\alpha }_{13}=\frac{-b^2{d}^2}{s_1{s}_3}$ ； $\Rightarrow \sin O_{13}=\sin \left(\pi -{\alpha }_{13}\right)=\sin {\alpha }_{13}=\frac{\left|BD\right|v}{s_1{s}_3}$

· 根据已知垂直交于BC棱的面角，解顶点位于O外心的互补对角的正弦、余弦代数值为：

见文 [6] 已知： ${\alpha }_{14}=\angle A{H}_{BC}D=\angle O_{ABC}{O}_{BC}{O}_{BCD}$， $\Rightarrow \cos {\alpha }_{14}=\frac{b^2{c}^2}{s_1{s}_4}$， $\Rightarrow \sin {\alpha }_{14}=\frac{\left|BC\right|v}{s_1{s}_4}$ ；

其互补对角： $O_{14}=\angle O_{ABC}O{O}_{BCD}=\pi -{\alpha }_{14}$

$\Rightarrow \cos O_{14}=\cos \left(\pi -{\alpha }_{14}\right)=-\cos {\alpha }_{14}=\frac{-b^2{c}^2}{s_1{s}_4}$ ； $\Rightarrow \sin O_{14}=\sin \left(\pi -{\alpha }_{14}\right)=\sin {\alpha }_{14}=\frac{\left|BC\right|v}{s_1{s}_4}$

· 根据已知垂直交于AD棱的面角，解顶点位于O外心的互补对角的正弦、余弦代数值为：

见文 [6] 已知： ${\alpha }_{23}=\angle B{H}_{AD}C=\angle O_{ABD}{O}_{AD}{O}_{ACD}$， $\Rightarrow \cos {\alpha }_{23}=\frac{a^2{d}^2}{s_2{s}_3}$， $\Rightarrow \sin {\alpha }_{23}=\frac{\left|AD\right|v}{s_2{s}_3}$ ；

其互补对角： $O_{23}=\angle O_{ABD}O{O}_{ACD}=\pi -{\alpha }_{23}$

$\Rightarrow \cos O_{23}=\cos \left(\pi -{\alpha }_{23}\right)=-\cos {\alpha }_{23}=\frac{-a^2{d}^2}{s_2{s}_3}$ ； $\Rightarrow \sin O_{23}=\sin \left(\pi -{\alpha }_{23}\right)=\sin {\alpha }_{23}=\frac{\left|AD\right|v}{s_2{s}_3}$

· 根据已知垂直交于AC棱的面角，解顶点位于O外心的互补对角的正弦、余弦代数值为：

见文 [6] 已知： ${\alpha }_{24}=\angle B{H}_{AC}D=\angle O_{ABC}{O}_{AC}{O}_{ACD}$， $\Rightarrow \cos {\alpha }_{24}=\frac{a^2{c}^2}{s_2{s}_4}$， $\Rightarrow \sin {\alpha }_{24}=\frac{\left|AC\right|v}{s_2{s}_4}$ ；

其互补对角： $O_{24}=\angle O_{ABC}O{O}_{ACD}=\pi -{\alpha }_{24}$

$\Rightarrow \cos O_{24}=\cos \left(\pi -{\alpha }_{24}\right)=-\cos {\alpha }_{24}=\frac{-a^2{c}^2}{s_2{s}_4}$ ； $\Rightarrow \sin O_{24}=\sin \left(\pi -{\alpha }_{24}\right)=\sin {\alpha }_{24}=\frac{\left|AC\right|v}{s_2{s}_4}$

· 根据已知垂直交于AB棱的面角，解顶点位于O外心的互补对角的正弦、余弦代数值为：

见文 [6] 已知： ${\alpha }_{34}=\angle C{H}_{AB}D=\angle O_{ABC}{O}_{AB}{O}_{ABD}$， $\Rightarrow \cos {\alpha }_{34}=\frac{a^2{b}^2}{s_3{s}_4}$， $\Rightarrow \sin {\alpha }_{34}=\frac{\left|AB\right|v}{s_3{s}_4}$ ；

其互补对角： $O_{34}=\angle O_{ABC}O{O}_{ABD}=\pi -{\alpha }_{34}$

$\Rightarrow \cos O_{34}=\cos \left(\pi -{\alpha }_{34}\right)=-\cos {\alpha }_{34}=\frac{-a^2{b}^2}{s_3{s}_4}$ ； $\Rightarrow \sin O_{34}=\sin \left(\pi -{\alpha }_{34}\right)=\sin {\alpha }_{34}=\frac{\left|AB\right|v}{s_3{s}_4}$

3. 总结

4球正交球心间连线间一至四维外接球半径、外心坐标、及其幂集间距算法及其互补对角的正弦、余弦的代数值的算法分别归纳如下：

3.1. 一至四维的外接球半径的平方具有同构的公式

一至四维球心间外接球半径的平方：等于同态维数与重心球半径之积方与同态维数减2与垂心球半径的积方之差的四分之一。一至四维(点、线、面、体)外接球半径与重心球半径、垂心球半径相关。其中二维外接球半径与二维重心球半径共球。

3.2. 一至四维的外心坐标具有同构的公式

一至四维球心间同态外心坐标：三个外心分坐标均为维数与同态重心分坐标积减维数减2与同态垂心分坐标之积的差的二分之一。一至四维(点、线、面、体)外心坐标与重心球垂心球球心坐标相关，其中：一维外心与同态重心、垂心共点；二维外心与同态重心共点。

3.3. 一至四维及其幂集的任意子集外接球球心间距(免坐标)的同构公式

一至四维及其幂集的任意子集外心间距(免坐标)同构计算公式为：其外心间距的平方等于外接球半径与其幂集的任意一个非空子集的外接球半径的平方差，幂集间均为垂直关系。

一至四维15点外心的间距数应有 $\frac{\left(15-1\right)\times 15}{2}=105$ 个。

其中：

任意维非零幂集存在外心间距数65个(其中：一维：4个、二维：3个 × 6棱 = 18个、三维：7个 × 4面 = 28个、四维：15个 × 1体 = 15个)，均可(免坐标)用公式(3)计算；

因一维、二维共10点外心均与一维、二维10点重心共点，间距数 $\frac{\left(10-1\right)\times 10}{2}=45$ 个，可(免坐标)用文 [3] 重心球球心间距公式计算(属幂集部分也可用公式(3)计算)；

其余无法使用上述(免坐标)计算间距的，均用2点坐标距离公式计算。

3.4. 一至四维的外心连线含有18组4点所围的4边形符合托勒密定理

其中：维数1 (2、2) 3间连线12组、维数2 (3、3) 4间连线6组四边形间，均可用4点共面的平面方程证明，因各组均存在一组对角各为90度，所以均可用托勒密定理：四边形两对对边乘积的和等于两条对角线的乘积，其18组线段关系等式，可以重新组合成新等式。

还可以根据文 [6] 用已知的棱角、面角的正弦余弦的代数值，直接得出其互补对角的相同正弦和负余弦的代数值。因此上述互补对角(钝角)也可以借用文 [6] 的相关棱正弦、余弦定理；和相关面角正弦、余弦定理。