锗石墨烯作为Li离子电池负极材料的第一性原理研究

First-Principles Study of Germagraphene as an Anode Material for Lithium-Ion Batteries

摘要: 采用基于密度泛函理论的第一性原理方法计算了Li在锗掺杂的AAAA型、AABB型和ABAB型石墨烯表面的吸附性质、态密度、电学性质及迁移行为。结果表明，三种掺杂石墨烯结构中，Li原子的稳定吸附位置都为Ge的次近邻H位和Ge原子凹侧上方的Ge-T位。AABB型锗掺杂石墨烯总能量最低，ABAB型锗掺杂石墨烯晶格变化最小，AAAA型锗掺杂石墨烯对Li原子的吸附能力最强。Li原子吸附后，AABB型和ABAB型的锗掺杂石墨烯在费米能级处的态密度提升比较大，产生的载流子更多，电子传导更好，有三个方向的电荷转移：Li→石墨烯、石墨烯→Ge和Li→Ge。Li在AABB型锗掺杂石墨烯表面主要沿1H→2H的迁移路径进行扩散，能垒仅为0.211 eV。研究表明三种结构中AABB型锗掺杂石墨烯更适合作锂离子电池的负极材料。

Abstract: The first-principles method based on density functional theory was used to calculate the adsorption properties, electronic density of states, electrical properties and migration behavior of Li on the surface of Germagraphene of AAAA, AABB and ABAB types. Among the three Germagraphene structures, the stable adsorption positions of Li atoms are both the next H-site of Ge and the Ge-T site above the concave side of Ge atoms. The total energy of AABB-Germagraphene is the lowest, the lattice change of ABAB Germagraphene is the lowest, and the adsorption energy of AAAA Germa-graphene to Li atoms is the strongest. After Li atom adsorption, the density states of AABB and ABAB Germagraphene improve greatly at the Fermi energy level, resulting in more carriers, better electron conduction, and three-direction charge transfer: Li→graphene, graphene→Ge and Li→Ge. Li diffuses on the surface of AABB Germagraphene mainly along the migration path from 1H to 2H with an energy barrier of 0.211 eV. The results show that AABB Germagraphene is more suitable for cathode material of lithium ion battery.

1. 引言

目前锂离子电池因其具有成本低、循环使用寿命长、绿色环保等优点被广泛应用。其负极材料多使用石墨，但石墨储锂容量仅为372 mAh/g [1]，且锂离子不易在石墨表面发生扩散和迁移。在循环过程中金属锂易形成锂枝晶，刺破隔膜材料从而引起电池短路，存在一定的安全隐患。

随着二维材料的快速发展，人们把目光投向二维材料作为电极材料 [2]。石墨烯独特的二维六角蜂窝状结构，具有高的载流子迁移率 [3] [4]、大的比表面积和不受温度影响等优点，Yoo等人研究表明，石墨烯储锂容量达到784 mAh/g [5]，是石墨储锂量的两倍，但石墨烯的载流子浓度偏低 [6] [7]，而掺杂石墨烯表现出更高的储锂量和更稳定的循环性质，因此掺杂石墨烯有望成为二次电池的电极材料。

人们使用第一性原理方法对材料的性能进行理论研究预测。例如：2009年Chi等人 [8] 使用第一性原理方法对H₂CO在本征石墨烯和铝掺杂石墨烯上的吸附进行研究，结果表明，由于H₂CO的化学吸附铝掺杂石墨烯体系具有较高的结合能值和较短的连接距离。H₂CO和Al掺杂石墨烯片之间可以看到轨道杂化，而在H₂CO分子和石墨烯片之间没有杂化。因此，铝掺杂石墨烯有望成为一种新型的H₂CO气体化学传感器。2014年，Noh等人 [9] 使用第一性原理方法对N掺杂石墨烯的氧还原反应进行研究，结果表明，过渡金属载体是控制掺杂石墨烯氧化还原反应机理的一种很有前途的方法。2015年，Pamungkas等人 [10] 使用第一性原理对镓掺杂硅的电子性质进行研究，结果表明镓掺杂改变了硅的半金属性质。2017年，Das等人 [11] 使用第一性原理对硼浓度的增加对单层硼掺杂碳片重量容量的影响进行研究，结果表明随着B浓度的增加，重量测定能力显著增强，直到x = 2，且均匀掺杂BC₂的存储容量最高。2018年，Wang H等人 [12] 使用第一性原理方法对硅掺杂石墨烯作为锂离子电池高容量负极材料的科学可行性进行研究，结果表明，硅石墨烯确保了石墨烯对锂的强吸附，从而存储更多锂，具有稳定性高、容量大的优点。2019年，Junping Hu等人 [13] 使用第一性原理研究对锗掺杂石墨烯作为锂离子电池负极材料进行研究，结果表明：锂吸附前后材料具有良好的导电性；Li在锗石墨烯上的扩散势垒较低，表明Li扩散速度较快；计算得到的平均插层电位很低(~0.03 V)，有利于提高电池的工作电压；此外，在锂插层过程中，材料的晶格变化较小(~0.48%)，表明材料具有良好的循环性能。因此，锗石墨烯是一种很有前途的锂离子电池高容量负极材料。

基于以上优点，虽然目前已经做出了锗石墨烯作为锂离子电池负极材料的理论预测且在实验方面研究制备，但是缺乏对掺杂锗的位置及其相关性质的详细研究。本文采用第一性原理方法对AAAA型、AABB型和ABAB型的锗掺杂石墨烯对Li原子的吸附性质、态密度、电荷密度和迁移行为进行了研究。比较三种不同构型之间的关系与差别，揭示不同构型对Li原子的吸附和迁移的影响，为锗掺杂石墨烯作为锂离子电池负极材料的应用提供进一步理论指导。

2. 计算方法和构建模型

2.1. 计算方法

本文计算使用基于密度泛函理论(DFT) [14] [15] 第一性原理方法的VASP [16] [17] [18] 软件包，研究了Li原子在AAAA型、AABB型和ABAB型的锗掺杂石墨烯结构表面吸附性质、态密度、电子性质及迁移路径。计算时选取投影缀加波赝势(PAW)和局域密度近似(LDA)分别计算电子、离子相互作用情况和电子交换相关情况。在所有的计算中，都将C 2s²2p²和Ge 4s²4p²作为价电子。平面波截断能为500 eV，布里渊区采用3 × 3 × 1的Monkhorst-Pack型网格 [19] 进行结构优化，采用5 × 5 × 1网格进行电子结构计算，能量的收敛精度为10⁻⁴ eV，力的收敛标准为0.5 eV/nm。选定锗掺杂石墨烯平面为aob平面，c轴垂直于锗掺杂石墨烯平面，为减小层间的相互作用，真空层取为20 Å。

本文计算了Li原子在石墨烯以及锗掺杂石墨烯体系不同位置的吸附能，吸附能由下面公式得到

$E_{\text{ad}}=\left[E_{\text{Germagraphene}+\text{Li}}-E_{\text{Germagraphene}}-n{E}_{\text{Li}}\right]/n$

式中 $E_{\text{Germagraphene}+\text{Li}}$ 是吸附Li原子后锗掺杂石墨烯总能量，E_{Germagraphene}是锗掺杂石墨烯总能量，E_Li是Li原子的总能量，n是Li原子的个数。

采用爬坡弹性带方法(CI-NEB)方法计算了Li原子在三种构型的锗掺杂石墨烯表面的迁移路径，利用第一性原理的方法计算Li原子沿不同路径迁移所需的能垒。

2.2. 构建模型

Tripathi等人实验 [20] 表明，锗可以直接替换石墨烯中的C原子，与相邻的三个C原子结合成键。由于Ge原子半径较大，打破了二维石墨烯的平面结构，形成弯曲的平面外结构。Junping Hu等人 [13] 对锗在石墨烯中的掺杂浓度进行了计算研究，结果表明，掺杂浓度为5.56% (1/18)的结构能达到最大的储Li容量(>1700 mAh/g)。我们在此基础上构建了6 × 6 × 1的石墨烯结构(72个原子)，掺杂4个Ge原子以保证最优的掺杂浓度，如图1(a)。我们将c轴正方向的石墨烯表面标注为A面、负方向为B面，由于Ge

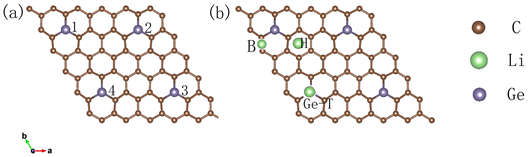
Figure 1. (a) Specific positions and serial numbers of four Ge atoms doped in graphenes; (b) adsorption positions of Li atom

图1. (a) 四个锗原子掺杂石墨烯具体位置及编号；(b) Li原子的吸附位置

原子掺杂之后的凸凹位置不同，将四个锗原子顺时针编号，且凸侧为A，凹侧为B，构建了如图2(a)、图2(b)和图2(c)所示的AAAA型、AABB型和ABAB型三种锗掺杂石墨烯结构。

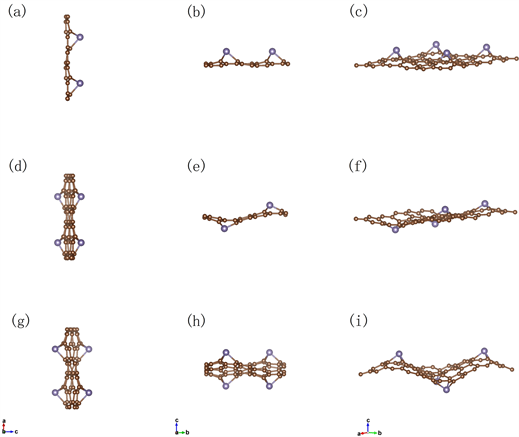
Figure 2. Top view (a) and side view (b) ,(c) of AAAA-Germagraphene; top view (d) and side view (e), (f) of AABB Germagraphene; top view (g) and side view (h), (i) of ABAB Germagraphene

图2. AAAA型锗掺杂石墨烯结构的俯视图(a)、侧视图(b)和(c)；AABB型锗掺杂石墨烯结构的俯视图(d)、侧视图(e)和(f)和ABAB型锗掺杂石墨烯结构的俯视图(g)、侧视图(h)和(i)

3. 结果与讨论

3.1. Li原子在锗掺杂石墨烯表面的吸附性质

为探讨三种构型锗掺杂石墨烯对Li原子的吸附性能情况，首先对结构进行优化。本征石墨烯结构优化后，晶格常数为14.684 × 14.684 Å，C-C键长为1.41~1.42 Å；锗掺杂石墨烯结构优化后，和C-C键相比，Ge-C之间的键角和键长均发生了改变，Ge原子远离平面凸起或凹下，使石墨烯平面产生形变。AAAA型锗掺杂石墨烯晶格常数为14.928 × 14.928 Å，AABB型锗掺杂石墨烯晶格常数为14.880 × 14.687 Å，ABAB型锗掺杂石墨烯晶格常数为14.691 × 14.691 Å。由此可见，ABAB型锗掺杂石墨烯晶格变化最小。

为研究Li原子在锗掺杂石墨烯表面的最佳吸附位置，分别选取了与Ge次近邻碳元环上方的中心空位(H)、碳碳键中心上方的桥位(B)和Ge原子凹侧正上方的顶位(Ge-T)进行吸附计算。

由表1可以看出，AABB型锗掺杂石墨烯总能量为−686.024 eV，明显低于AAAA型和ABAB型锗掺杂石墨烯的总能量，即最易形成。Li原子在AAAA、AABB和ABAB型三种锗石墨烯Ge-T位的吸附能分别为−0.923 eV、−0.836 eV和−0.823 eV，吸附高度分别为0.066 Å、0.038 Å和0.043 Å，在H位的吸附能分别为−0.471 eV、−0.371 eV和−0.358 eV，吸附高度分别为0.085 Å、0.094 Å和0.103 Å，由此可知，AAAA型锗掺杂石墨烯对Li原子的吸附能力最强。三种构型的锗掺杂石墨烯Ge-T位和H位为稳定吸附位置，吸附能力强、吸附高度低。Li原子在吸附过程中会引起结构晶格常数的微小变化，可以忽略。

Table 1. The total energy of AAAA Germagraphene, AABB Germagraphene and ABAB Germagraphene (EGermagraphene), total energy of Li adsorption on its surface (EGermagraphene+Li), adsorption energy (Ead), vertical distance between Li and graphene plane (d), and charge transfer of Li atom adsorption at stable position Q

表1. AAAA、AABB和ABAB型锗掺杂石墨烯的总能量E_{Germagraphene}、Li在其表面吸附后的总能量E_{Germagraphene+Li}、吸附能E_ad、Li与石墨烯平面的垂直距离d和Li原子吸附在稳定位置时的电荷转移Q

3.2. Li在锗掺杂石墨烯吸附前后的态密度

为了检验Li原子吸附前后材料是否保持导电性，我们计算了电子态密度。由图3可以看出，在Li原子吸附之前，三种构型的锗掺杂石墨烯在费米能级处的态密度都为0，且靠近费米能级处的态密度主要由C轨道提供。在Li原子吸附后，锗掺杂石墨烯的三种构型在费米能级处的态密度都有很大提高。其中，AAAA型锗掺杂石墨烯提高了18.8 eV，AABB型锗掺杂石墨烯提高了68.57 eV和ABAB型锗掺杂石墨烯提高了76.98 eV，态密度提升的越多，意味着系统中产生的载流子浓度越多，说明电子传导更好，可以更好的应用在锂离子电池中。

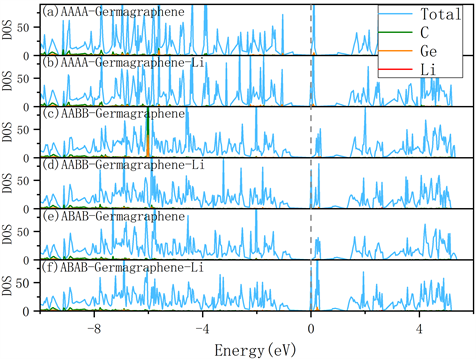
Figure 3. Density of states for (a) AAAA Germagraphene, (b) AAAA Germagraphene with Li adsorption, (c) AABB Germagraphene, (d) AABB Germagraphene with Li adsorption, (e) ABAB Germagraphene, and (f) ABAB Germagraphene with Li adsorption

图3. (a) AAAA型锗掺杂石墨烯、(b) AAAA型锗掺杂石墨烯(Li吸附)、(c) AABB型锗掺杂石墨烯、(d) AABB型锗掺杂石墨烯(Li吸附)、(e) ABAB型锗掺杂石墨烯和(f) ABAB型锗掺杂石墨烯(Li吸附)的态密度图

3.3. Li原子在锗掺杂石墨烯表面的电学性质

为了进一步探讨锗掺杂对石墨烯表面电学性质的影响，观察Li原子与石墨烯之间的电荷转移，分别计算了锗掺杂的AAAA型、AABB型和ABAB型石墨烯的差分电荷密度。图4为三种构型的三维差分电荷密度图(CDD)。黄色部分代表成键之后电荷密度的增加。蓝色部分代表成键之后电荷密度的减少。

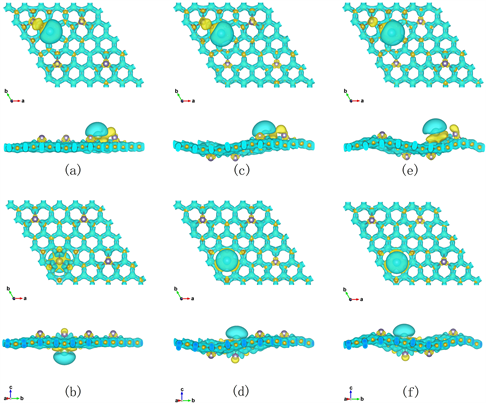
Figure 4. Top and side view of the CDD induced by Li atom adsorption on the (a) H site and (b) Ge-T site of AAAA Germagraphene; (c) H site and (d) Ge-T site of AABB Germagraphene; and (e) H site and (f) Ge-T site of ABAB Germagraphene respectively

图4. Li原子在AAAA型锗掺杂石墨烯表面(a)次近邻H位和(b)Ge-T位；AABB型锗掺杂石墨烯表面(c)次近邻H位和(d) Ge-T位；ABAB型锗掺杂石墨烯表面(e)次近邻H位和(f) Ge-T位的三维差分电荷密度的俯视图和侧视图

可以看出，Li原子在三种构型的锗掺杂石墨烯表面吸附后，与表面区域存在一定差分电荷密度的分布。Li原子周围呈现蓝绿色，附近的石墨烯周围呈现黄色，说明Li原子周围的电荷密度在减少，Li原子附近的C原子的电荷密度在增加，即Li原子失去电子，Li原子附近的C原子得到电子，Li原子上的电荷转移到了附近的石墨烯上；Ge原子周围呈现黄色，Ge原子附近的石墨烯周围呈现蓝绿色，说明Ge原子周围的电荷密度在增加，Ge原子附近的C原子周围电荷密度在减少，即Ge原子得到电子，Ge原子附近的C原子失去电子，石墨烯上的电荷转移到了附近的Ge上；Li原子周围呈现蓝绿色，Ge原子周围呈现黄色，Li原子失去电子，Ge原子得到电子，Li原子上的电荷转移到了Ge原子上。

通过Bader布局分析，可知Li吸附在三种构型的锗掺杂石墨烯的Ge-T位电荷转移量分别为0.86e、0.87 e和0.87 e，H位电荷转移量分别为0.87 e、0.88 e和0.88 e，相同吸附位置电荷转移量都基本一致，见表1。

3.4. Li原子在锗掺杂石墨烯表面的迁移行为

为研究Li原子的迁移行为，本文采用了爬坡式弹性带(CI-NEB)方法来计算扩散能垒高度，寻找最优的扩散路径。其中AAAA型锗掺杂石墨烯的扩散路径采用与Junping Hu等人 [13] 计算的A面PATH-2路径相同，Hu计算的能垒为0.151 eV，我们的计算结果为0.157 eV，说明我们的计算方法是可行的。用此方法计算了AABB型和ABAB型锗掺杂石墨烯表面的Li原子迁移路径及能垒。由于AABB型锗掺杂石墨烯的形成能要更低，我们接下来将主要介绍Li原子在AABB型锗掺杂石墨烯的迁移。

对于AABB型锗掺杂石墨烯，本文考虑了Li原子在其表面的5种可能迁移路径，见图5，分别为3Ge-T→4Ge-T、1H→4Ge-T、3Ge-T→4H、1H→1H和1H→2H，分别计算了迁移路径中过渡态的位置。

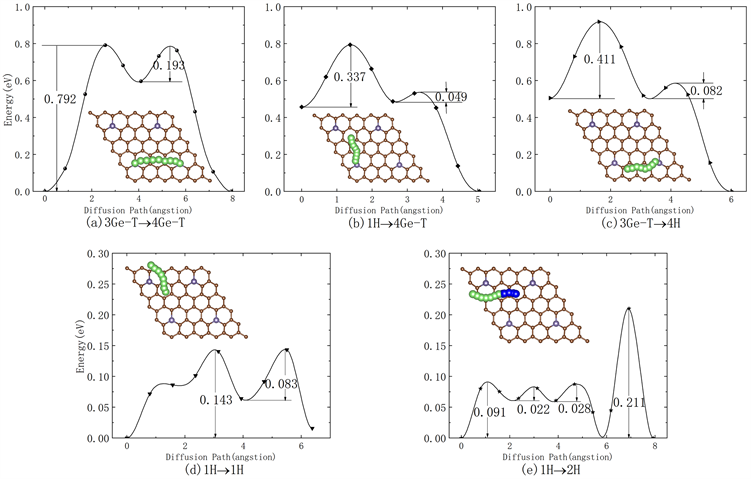
Figure 5. Diffusion pathways and diffusion energy curves of Li atoms on the surface via the (a) 3Ge-T→4 Ge-T, (b) 1H→4Ge-T, (c) 3 Ge-T→4H, (d) 1H→1H and (e) 1H→2H diffusion pathway, respectively

图5. Li原子在AABB型锗掺杂石墨烯表面沿(a) 3Ge-T→4Ge-T、(b) 1H→4Ge-T、(c) 3Ge-T→4H、(d) 1H→1H和(e) 1H→2H的迁移路径和迁移能垒曲线

计算结果表明，Li原子在AABB型锗掺杂石墨烯表面沿3Ge-T→4Ge-T路径迁移时，见图5(a)，对应的能垒为0.792 eV，小于AAAA型的B面迁移路径的0.837 eV [13]。Li原子在AABB型锗掺杂石墨烯表面沿1H→4Ge-T和3Ge-T→4H路径迁移的能垒分别为0.337 eV和0.411 eV。为了和AAAA型锗掺杂石墨烯的Li原子迁移路径对比，选择了同样的1H→1H路径，得到的能垒为0.143 eV，小于AAAA型的0.151 eV，但对于AABB型锗掺杂石墨烯而言，此路径的初位置和末位置不是等价位置，且考虑到完整路径的影响，我们计算了如图5(e)所示1H→2H的路径，其中绿色路径为1号锗原子的等价H位的迁移路径，能垒为0.091 eV，蓝色为1号锗的H位到2号锗H位的迁移路径，能垒为0.211 eV。说明Ge原子掺杂石墨烯后的凸凹位置不同，对Li原子的迁移路径产生一定的影响，Li原子更易在AABB型锗掺杂石墨烯表面沿1H→2H路径迁移，即AABB型锗掺杂石墨烯是一种适合Li离子迁移的材料构型。

4. 结论

本文采用了基于密度泛函理论的投影缀加平面法，使用VASP软件包研究了Li原子在AAAA型、AABB型和ABAB型锗掺杂石墨烯表面的吸附性质、态密度、电学性质及迁移行为，结果表明：

1) Li原子在AAAA型、AABB型和ABAB型的锗掺杂石墨烯表面的稳定吸附位置都是Ge次近邻的H位和Ge凹侧上方Ge-T位。AABB型锗掺杂石墨烯的形成能最低，即最易形成AABB型。ABAB型锗掺杂石墨烯对晶格产生的影响最小，循环性能更佳。

2) Li原子吸附后，三种构型的锗掺杂石墨烯仍然保持金属性，AABB型、ABAB型的锗掺杂石墨烯在费米能级处的态密度提升的比较大，产生的载流子更多，电子传导性更好。

3) Li原子吸附在锗掺杂石墨烯体系表面后，有三方向的电荷转移：Li→石墨烯、石墨烯→Ge，Li→Ge。

4) Li原子在AABB型锗掺杂石墨烯表面主要沿1H→2H的迁移路径进行扩散，扩散能垒仅为0.211 eV。扩散能垒低，说明扩散速率高、充电快。

综上，三种结构中，AABB型锗掺杂石墨烯具有形成能低、循环性能佳、导电性好和Li扩散能垒低等优点，故更适合作锂离子电池的负极材料。

NOTES

^*第一作者。

^#通讯作者。