1. 引言
著名的蔡氏电路 [1] 是由美籍华裔科学家蔡少棠教授在1983年提出,它是非线性电路中产生复杂动力学行为的常见混沌振荡电路 [2] [3]。在蔡氏电路中,通过改变其拓扑结构或参数,运用Matlab数值模拟 [4] 对电路系统中混沌行为进行研究,能够观察到系统存在混沌吸引子,从而产生分岔 [5]、单涡卷、双涡卷吸引子 [6] 等丰富的混沌现象。
蔡氏电路是以分段线性电阻为核心,在不同的参数组合下产生了极其丰富的分岔与混沌现象。此外,簇发振荡 [7] [8] 作为快慢动力系统的典型代表行为,在频率激励影响下有大幅度振荡和小幅度振荡,普遍存在于神经科学、物理实验 [9] 等领域。目前一些学者正在研究蔡氏电路的各种变形模式,通过改变原电路的非线性元件或添加新元件来研究混沌现象,如刘崇新等人研究一类对偶和负电容的蔡氏电路,Hartley等人研究用三次方模块代替原来的分段线性模块;但研究蔡氏电路在双频激励下的情况较少。
因此本文将针对一类含双频激励的变形蔡氏电路 [10] 的数学模型展开研究,从理论上分析不同参数下的动力学行为,并数值模拟分岔图、相图、时间序列图等讨论系统的混沌演化过程,以及这类非光滑系统 [11] [12] [13] 的不同尺度效应和簇发振荡现象,对于研究非光滑和多尺度因素下的双激励频率系统的复杂性及机理具有一定指导意义。
2. 蔡氏电路数学模型
本文考虑的这类变形蔡氏电路的数学模型如下:
,其中
(1)
且
,
,
为蔡氏电路无量纲化对应参数。
3. 平衡点和分岔分析
根据非线性电阻无量纲
方程的三种形式可将状态空间分为三个子空间,即:
(2)
不连续边界为
,当激励频率满足
,
时,可能出现两个时间尺度的快慢系统,因此相应的子系统
控制该系统的非线性动力学行为。
我们知道,该系统行为由
和
三个区域控制,分岔参数
为慢变量。对于上述三维自治系统,平衡态由
决定,存在三个平衡点
和
。
对于子系统
和
,其平衡点为
,
和
,其中
满足:
,这里
和
处相应的雅克比矩阵为:
(3)
平衡点
处的稳定性由特征方程确定,它的形式如下:
(4)
假设
时,
,这表明
是稳定的双曲平衡点,即在两个子系统
和
中,没有与平衡点相关的分岔现象。
同理,平衡点
处的特征方程如下:
(5)
由平衡点
处的折叠分岔知道,当
时,若
,表明对于
可能发生折叠分岔,同时在每个分岔处存在一个零特征值,会导致系统出现跳跃行为,当
时,若
,
且
可能发生hopf分岔。
我们采用Matlab软件对系统非线性微分方程组进行求解,积分步长取
,不妨令
,数值模拟x关于
的分岔图。设置参数如下:
(6)
数值结果表明:在不连续边界
处产生hopf分岔,此时
出现极限环,然后出现C分岔,
,出现超临界hopf分岔,进而到折叠分岔,如图1所示。
4. 双频激励的相空间吸引子
现对方程采用四阶Runge-Kutta法,初始值为
,调节参数a得到不同特性相图,观察系统的运动状态。固定
,并保持其他参数不变,不妨令
时数值模拟如下:
通过改变a的值,我们发现系统的混沌吸引子运动轨迹发生显著变化,如当
时,有两个共存的混沌吸引子,即双涡卷吸引子,这从图2(a)~(c)的相轨迹看出,接着如图2(d)~(f)所示,当
时双涡卷吸引子形态发生改变,轨线变得密集而随机,而当
时双涡卷吸引子变为一个单独的混沌吸引子,轨线绕环运动;同理考虑参数b也能得到类似结果。当然,激励项的振幅和频率也紧密影响着系统的非线性动力学行为。
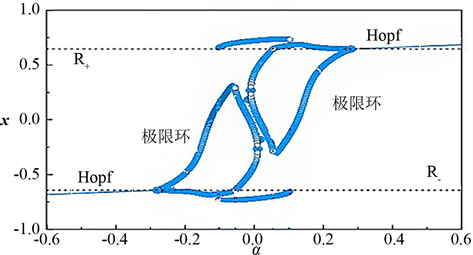
Figure 1. Bifurcation diagram of x about α
图1. x关于α的分岔图
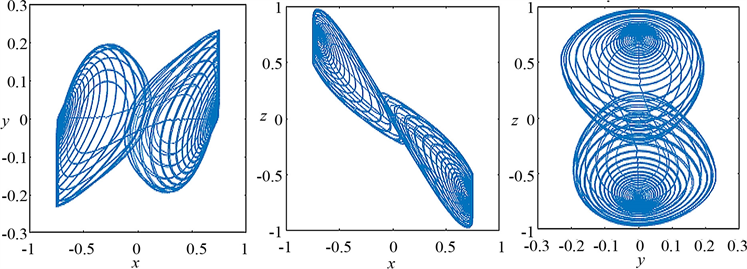 (a) (b) (c)
(a) (b) (c) 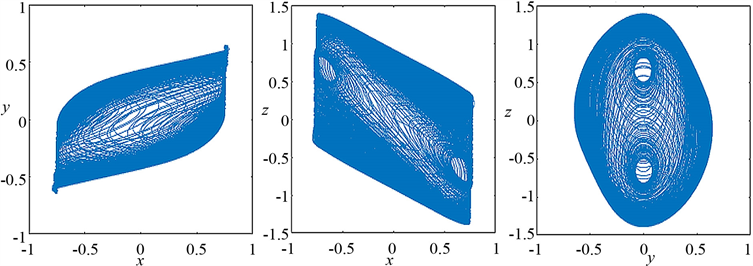 (d) (e) (f)
(d) (e) (f) 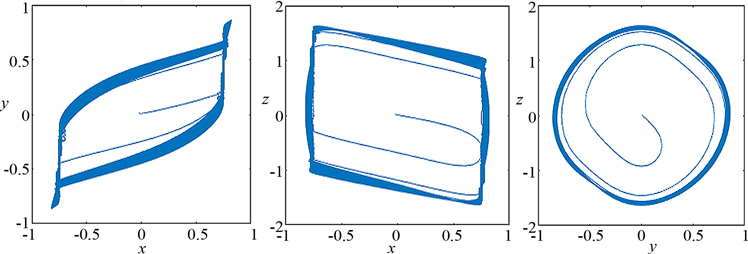 (g) (h) (i)
(g) (h) (i)
Figure 2. Is about the phase diagram of x-y, x-z, y-z, when
图2. 关于x-y,x-z,y-z的相图,此时
5. 双频激励的簇发现象
当系统方程中激励项的频率远小于固有频率时,存在不同的时间尺度,且不同的分岔行为会影响系统的静止态和激发态,两者相互发生转换,从而导致不同行为的簇发振荡现象。在簇发振荡行为中静止态用QS表示,激发态用SP表示。
5.1. 两个激励频率相同时的簇发振荡
设置参数
,且
,当
时的时间序列图。
 (a) (b)
(a) (b) 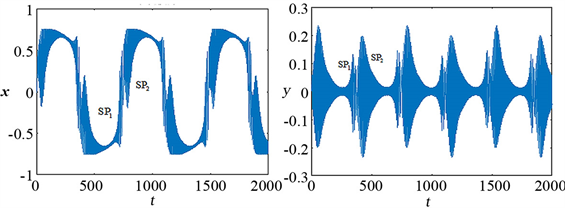 (c) (d)
(c) (d) 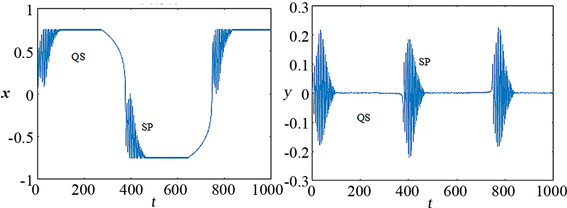 (e) (f)
(e) (f)
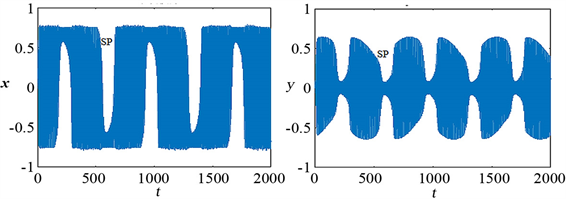
Figure 3. Is about the phase diagram of x-t, y-t, when
.
图3. 关于x-t,y-t的时间序列图,此时
如图3所示,系统表现为关于原点对称的周期振荡,此时簇发振荡存在着两种不同的阶段,一是相对平缓状态,对应于静止态,二是相对剧烈的大幅振荡状态,对应于激发态。
我们可以发现,随激励振幅的增大,吸引子产生复杂的簇发振荡。如图3(a)、(b)所示,当
时,系统出现一组对称的簇发振荡,非光滑hopf分岔包含激发态的吸引子;当
时,如图3(c)、(d)所示,当
时,系统将分成两个不对称的激发态,SP分成SP1和SP2两个阶段,当
时,如图3(e)、(f)所示,当
时,可观测到系统吸引子在静止态和激发态之间相互转换,呈现出快变振荡和慢变振荡交替进行的簇发现象。
5.2. 两个激励频率不同时的簇发振荡
我们考虑系统的两个激励频率的关系为
,这里
,不改变初始条件并固定其他参数不变,选定
,作出系统相图、时间序列图来分析系统非线性动力学行为。
设置三组参数
,
,
进行数值模拟。
 (a) (b)
(a) (b) 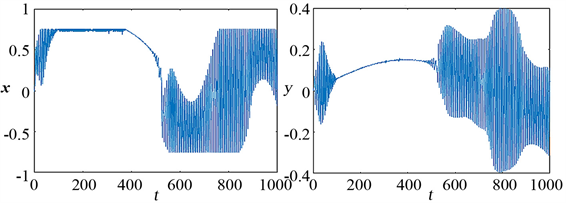 (c) (d)
(c) (d) 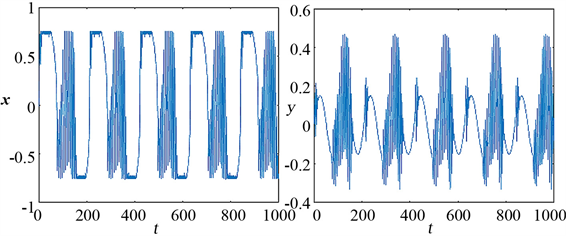 (e) (f)
(e) (f) 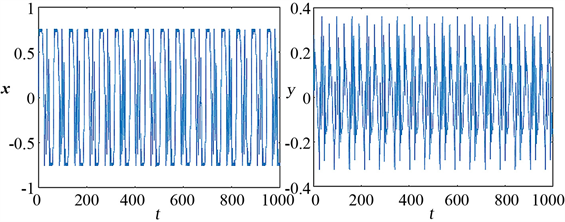 (g) (h)
(g) (h)
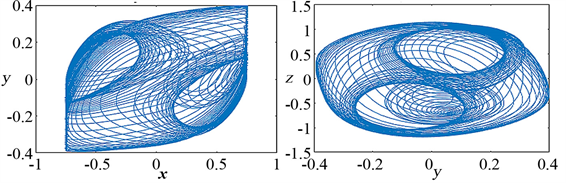
Figure 4. (a), (b), (c) and (d) shows the system phase diagram and time series diagram when
,
, and (e), (f), (g) and (h) shows time series diagrams when
,
and
,
图4. 系统相图和时间序列图,此时
,
,
,
,
,
如图4当两个不同的激励频率成整数比改变时,系统吸引子轨迹呈现复杂的运动形态,即在每个周期内出现两个不对称的簇发振荡状态,从小幅度振荡跃迁到大幅度振荡。如当
时,图4(a)、(b)反映的是系统的双涡卷吸引子相图,这不同于之前的混沌吸引子状态,从(c)、(d)中发现系统由较小幅度的簇发振荡过渡到相对平缓的静止态,然后跃迁到大幅度的剧烈振荡。当
时,如图(e)、(f)激发态吸引子会出现分裂,两者振荡频率明显。随激励频率的增大,同样可呈现出快慢交替进行的簇发现象。
6. 结论
蔡氏电路有着丰富复杂的混沌动力学特征,本文从理论分析与数值模拟两方面研究这类变形蔡氏电路的分岔、混沌和簇发现象。利用系统平衡点处的Jacobi矩阵,定性分析系统的分岔行为,以及不同参数下的混沌现象,同时数值模拟验证了簇发振荡过程中出现的双涡卷混沌吸引子。研究结果表明在相同的混沌行为下,数值模拟与理论分析结论吻合,从图像上能准确地观察到混沌吸引子的行为特征。