1. 引言
1952年Wilkinson和Fishcher合作确定了二茂铁FeCp2的化学结构 [1],由此开启了金属夹心三明治团簇研究的序幕。迄今为止已有很多不同种类的金属夹心三明治团簇结构被实验合成或者理论研究。在金属夹心三明治团簇中,我们将其中的环状化合物称为配体,配体种类从早期的C5H5到苯环C6H6再到C7H7、C8H8等有机环状分子。1995年,Kaya和Nakajima [2] 课题组使用激光蒸发技术合成了稳定的线性苯夹钒三明治团簇结构VnBzn+1(Bz = benzene = C6H6)。上世纪末,Kurikawa [3] 等研究者对过渡金属和苯环组成的三明治团簇结构进行了实验研究分析。随后的研究扩展到双环有机结构配体,比如萘环C10H8。Li等对Vn−1Npn (n = 2~5)团簇结构和一维无限长纳米线结构进行了理论分析和研究 [4]。随着研究的深入,无机环状配体也进入了研究者的视野,将无机环状化合物环硼氮烷B4N4H8和C60作为配体研究金属夹心三明治团簇的结构与性质。有研究者还对Eun(B4N4H8)n+1 (n = 1~4)及其一维纳米线的结构和电子性质进行了系统的研究 [5] - [23]。
有趣的是,在对金属夹心团簇的研究中发现,它们的几何结构主要决定于夹心金属的种类,早期研究的(Sc, V, Ti)与苯分子构成的团簇多为线性多层结构,后期研究的(Fe, Co, Ni)构成的团簇多为米团结构。我们研究金属夹心三明治团簇是由于其在自旋电子学、分子识别,生物传感器等方面具有广泛的应用潜力。
我们在苯分子夹钒原子三明治团簇的基础上,将极性苯分子(4-氰基苯胺、4,5-二氨基邻苯二腈)作为配体与钒原子构建三明治团簇,并对其结构和磁学特性进行了系统的研究。在下面的讨论中,4-氰基苯胺简称为C7N2H6或者单CN分子,4,5-二氨基邻苯二腈简称为C8N4H6或者双CN分子。我们一方面探究官能团修饰对磁性的影响,另一方面探究极性分子在三明治结构中的排列行为。本研究不仅有助于丰富配体种类,而且为寻找具有新颖磁电性质的有机材料提供了一条途径。
2. 研究方法
所有计算均采用了DFT计算程序——Dmol3,以Dmol3的2017版本为主程序,计算采用广义梯度近似下的PBE (Predew-Burke-Ernzerhof)交换关联泛函 [24]。对结构进行优化时,K点选择1 × 1 × 1,截断能设置为450 eV,能量收敛判据设置为10−5 eV,力的收敛判据设置为2*10−3 eV/Å,对各个结构计算充分弛豫得到收敛结构。我们随后对各结构采用Gaussian 16w进行验证,所有体系采用密度泛函理论的B3LYP方法以及6-311G**基组,精度采用Gaussian 16w的默认精度,对所有团簇结构充分地进行弛豫得到能量更稳定的基态结构。两种计算结果在排除了基组和计算方法的误差之后其结果质量等价。
3. 结果与讨论
3.1. 极性苯分子C7N2H6夹钒原子三明治团簇结构
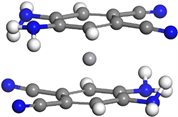
首先,我们构建了双层三明治团簇结构V(C7N2H6)2,即由两个C7N2H6分子夹一个钒原子。因为我们采用的是极性苯分子C7N2H6,所以我们考虑团簇构型可能呈现铁电排列或者是反铁电排列:前者对应于第一层的C7N2H6分子的-CN正对第二层的-CN,第一层的-NH2正对第二层的-NH2;后者对应于第一层的C7N2H6分子的-CN正对第二层的-NH2,第一层的-NH2正对第二层的-CN。我们进一步考虑团簇的构型也可能在第一层和第二层之间有一定的偏转角,所以在正对的基础上均加上15˚和30˚的偏转角。我们由这些构型作为初始构型进行充分的弛豫。在本文中,我们将一层分子中-CN官能团的碳和氮原子以及另一层分子中-CN官能团的碳原子组成一个平面,则另一层分子中C≡N键与该平面所形成的角度称为两层分子之间的偏转角。计算结果表明初始为铁电排列及其偏转15˚和30˚的三个构型经几何优化后偏转角依次变为5.966˚、0.502˚和70.855˚;初始为反铁电排列及其偏转15˚和30˚的三个构型经几何优化后偏转角依次变为4.3˚、7.633˚和1.483˚。对比以上六个优化构型的能量发现,偏转角为4.3˚的构型具有最低能量,因而最为稳定。据此确定了基态为反铁电排列,其构型如图1左上图所示。
对于三层三明治团簇结构V2(C7N2H6)3,我们继续选择了铁电排列和反铁电排列结构,对比之后最终得到三层的基态结构仍然呈现反铁电排列。我们观察到相较于双层结构,分子层间的偏转角变大,第一层C7N2H6分子与第二层偏转角为16.5˚,第二层与第三层偏转角为7.7˚,两个钒原子之间的间距为3.481Å,如图1右上图所示。
对于四层V3(C7N2H6)4的基态结构,首尾两层C7N2H6分子几乎正对,偏转角为0.79˚,中间夹心的两层偏转角为3.15˚,两个角度可以认为偏转不大,而第一层与第二层偏转角为29.17˚,偏转明显。三个钒原子之间的间距为3.447 Å和3.446 Å,间距对称,钒–钒平均间距较三层结构缩小,如图1左下图所示。
对于五层V4(C7N2H6)5的基态结构,第一层与第二层偏转角为9.03˚,第三~四层和第四~五层间偏转角依次为13.78˚和6.1˚,第二~三层偏转角为57.96˚,偏转明显,整体较为无序。四个钒原子间距依次为3.470 Å、3.372 Å和3.476 Å,间距对称,较四层结构钒–钒平均间距减小,如图1右下图所示。
3.2. 极性苯分子C8N4H6夹钒原子三明治团簇结构
基于对C7N2H6夹V三明治团簇的研究,在构建双层三明治团簇结构V(C8N4H6)2时,我们依旧考虑铁电排列和反铁电排列构型,并增加在正对基础上各加上15˚和30˚的偏转角的初始构型,然后对这些构型进行充分的弛豫,最终也确定了C8N4H6夹钒原子双层三明治团簇的基态结构为反铁电结构,第一层和第二层分子之间的偏转角很小,仅为1.49˚,如图2左上图所示。
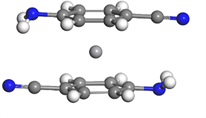 V(C7N2H6)2
V(C7N2H6)2 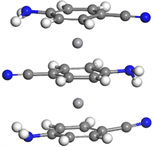 V2(C7N2H6)3
V2(C7N2H6)3 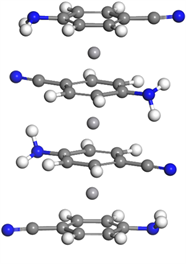 V3(C7N2H6)4
V3(C7N2H6)4 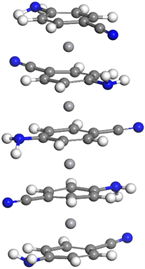 V4(C7N2H6)5
V4(C7N2H6)5
Figure 1. Molecular structure of Vm(C7N2H6)n (m = 1~4, n = m + 1)
图1. Vm(C7N2H6)n (m = 1~4, n = m + 1)团簇的基态分子结构图
对于三层三明治团簇结构V2(C8N4H6)3,我们选择了铁电排列和反铁电排列构型,得到的基态结构中第一层与第二层C8N4H6分子之间偏转角为32.8˚,第二层与第三层偏转角为10.2˚,两个钒原子之间间距为3.489 Å,如图2右上图所示。
对于四层V3(C8N4H6)4结构,第一和第二层C8N4H6分子几乎正对,之间的偏转角为1.156˚,第三和第四层之间的偏转角为3.982˚,而第二和第三层之间的偏转角为15.89˚,偏转明显,三个钒原子之间的间距为3.437 Å和3.433 Å,间距对称,较三层结构钒–钒平均间距缩小,如图2左下图所示。
我们继续对五层V4(C7N2H6)5结构进行了研究,计算结果表明从上到下偏转角依次为10.44˚、26.76˚、10.63˚、16.56˚,整体较为无序。四个钒原子间距依次为3.457 Å、3.341 Å、3.451 Å,间距较为对称,平均间距较四层结构明显减小,如图2右下图所示。
我们采用同样的计算方式和参数设置,计算了苯分子夹钒原子三明治团簇结构作为参照进行对比。表1列出了三种三明治团簇从三层到五层的钒–钒平均间距。

Table 1. The average V-V spacing of three sandwich cluster structures VmBzn, Vm(C7N2H6)n and Vm(C8N4H6)n (m = 1~4, n = m + 1)
表1. 三种三明治团簇VmBzn、Vm(C7N2H6)n、Vm(C8N4H6)n(m = 1~4, n = m + 1)的V-V平均间距
从表1中我们可以看到三种三明治团簇构型均随着层数的增加,钒–钒平均间距减小,其中配体为苯分子的三明治团簇结构钒–钒平均间距下降很慢,但是极性分子C7N2H6和C8N4H6作为配体使得钒–钒原子平均间距下降很快,并且双极性的C8N4H6分子对应的钒–钒原子平均间距下降最快。我们认为是有机官能团-CN和-NH2引起,原因在于-CN电负性较强带负电,而-NH2电负性较弱带正电,基态为反铁电性排列的方式让带正电的-NH2和带负电-CN相互吸引,从而导致团簇整体层间距减小。这个特征和苯夹钒三明治团簇存在明显差异。
 V(C8N4H6)2
V(C8N4H6)2  V2(C8N4H6)3
V2(C8N4H6)3  V3(C8N4H6)4
V3(C8N4H6)4 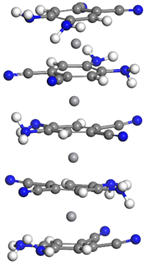 V4(C8N4H6)5
V4(C8N4H6)5
Figure 2. Molecular structure of Vm(C8N4H6)n (m = 1~4, n = m + 1)
图2. Vm(C8N4H6)n (m = 1~4, n = m + 1)团簇的基态分子结构图
3.3. 热力学稳定性
为了研究VmBzn、Vm(C7N2H6)n、Vm(C8N4H6)n (m = 1~4, n = m + 1)三种三明治团簇的热力学稳定性,我们计算了m = 1~4层各基态结构的结合能,团簇的结合能E(m, n)定义如下 [4]:
其中,m代表钒原子数,n代表配体分子数,E[V]代表优化后的钒原子能量,E[X]代表三种配体benzene分子、C7N2H6分子、以及C8N4H6分子优化后的能量,E[VmXn]代表优化后VmBzn、Vm(C7N2H6)n、Vm(C8N4H6)n (m = 1~4, n = m + 1)团簇结构的能量。计算得到的结合能如图3(a)所示。从图中我们可以看到各层结构得到的结合能均为正值,说明团簇结合过程是放热过程,因而团簇结构具有较强的稳定性。两种极性分子构型的团簇随着层数的增加,结合能逐渐减小,但是减小的速度明显放缓,并且V4(C8N4H6)5结合能有较小幅度的回升。我们可以预判,随着层数的增加,减小的速度会更小,推广到无限长的一维纳米线结构在热力学上也是稳定的。对于两种极性分子构成的三明治团簇结构在相同的层数时,Vm(C8N4H6)n结构较于Vm(C7N2H6)n结构结合能较小,说明在相同层数时,单CN分子和钒组成的三明治团簇结构更加稳定。
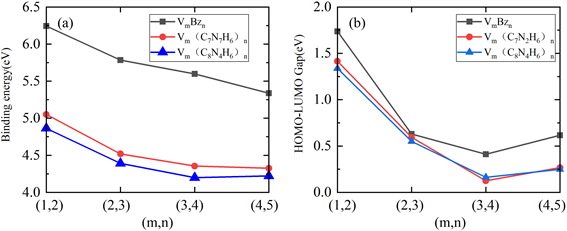
Figure 3. The binding energy (a) and HOMO-LUMO gap (b) of Vm(Bz)n, Vm(C7N2H6)n, and Vm(C8N4H6)n (m = 1~4, n = m + 1) sandwich clusters
图3. Vm(Bz)n、Vm(C7N2H6)n和Vm(C8N4H6)n (m = 1~4, n = m + 1)三明治团簇的结合能(a)和能隙(b)
图3(b)显示出三种配体夹钒原子三明治团簇HOMO-LUMO能隙及其趋势。这里HOMO和LUMO分别代表最高占据分子轨道(Highest Occupied Molecular Orbital)和最低未占分子轨道(Lowest Unoccupied Molecular Orbital)。我们发现三种构型从二层增加到四层时能隙都呈下降趋势。能隙越小,说明电子在外加电场影响的时候从占据轨道激发到空轨道更加容易。三种构型的五层结构相对于四层结构,能隙均有一定程度的上扬。Wang [25] 研究了苯钒三明治团簇结构,并发现对于V4Bz5,Jahn-Teller效应引起的结构形变使得团簇的对称性降低和轨道简并度下降,从而导致团簇的能量进一步下降。同理,极性分子构成的五层V4(C7N2H6)5和V4(C8N4H6)5三明治团簇也可能由Jahn-Teller效应引起HOMO-LUMO能隙的反常上扬。
3.4. 磁学性质
为了研究两种极性配体C7N2H6和C8N4H6夹钒原子三明治团簇结构的磁学性质,我们对每个结构都考虑了铁磁(FM)和反铁磁(AFM)两种构型,计算结果显示两种配体的团簇都是在二、四、五层结构呈铁磁排列,而在三层三明治团簇结构时呈反铁磁排列,但是三层结构的铁磁态和反铁磁态之间的能量差均极小,几近简并。我们将两种构型的计算结果在表2中列出,同时还给出了Vm(Bz)n三明治团簇的结果。


Table 2. Ground magnetic state (GMS), energy difference between AFM and FM states (ΔEAFM-FM), and total magnetic moment (TMM) for a series of Vm(Bz)n, Vm(C7N2H6)n and Vm(C8N4H6)n (n = 1~4, m = n + 1) sandwich clusters
表2. Vm(Bz)n、Vm(C7N2H6)n和Vm(C8N4H6)n (m = 1~4, n = m + 1)三明治团簇的基态、铁磁和反铁磁态能量差、以及总磁矩
从表2中我们可以看到Vm(Bz)n三明治团簇结构均呈铁磁基态,每个结构的铁磁基态和最高能量的反铁磁态之间的能量差在16~20 meV的范围变化。极性分子构成的Vm(C7N2H6)n和Vm(C8N4H6)n团簇结构除了三层三明治结构基态呈反铁磁态外,与Vm(Bz)n相类似,都是随着团簇的尺寸增加,磁矩也逐渐增加。与Vm(Bz)n团簇显著不同的是,极性分子构成的两种三明治团簇构型的ΔEAFM-FM随着团簇尺寸的增
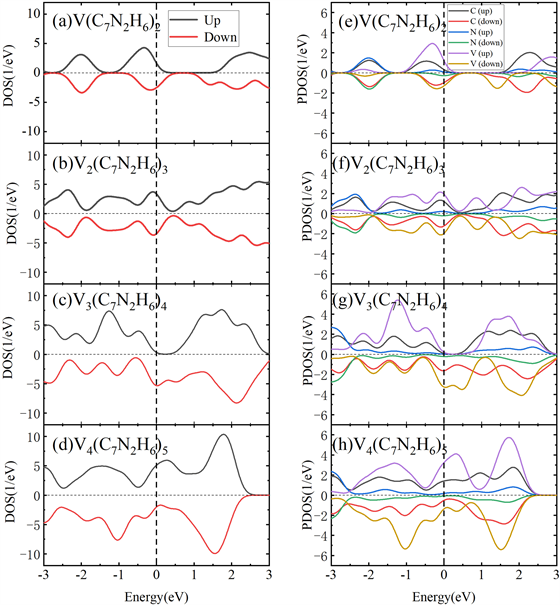
Figure 4. The DOS and PDOS of Vm(C7N2H6)n (m = 1~4, n = m + 1) sandwich clusters
图4. Vm(C7N2H6)n (m = 1~4, n = m + 1)三明治团簇的总态密度图和分波态密度
加呈不断增大,标志着铁磁基态随层数增加变得更加稳定。我们在计算极性分子构成的三明治团簇结构过程中发现钒原子的磁矩并不严格为1 μB,随着层数的增加从0.98 μB至1.39 μB变化,并且磁矩大小呈近似对称分布,例如V2(C7N2H6)3,两个钒原子的磁矩为1.283 μB和1.28 μB,V3(C7N2H6)4中三个钒原子的磁矩依次为1.34 μB、0.983 μB和1.34 μB,而五层团簇由于Jahn-Teller效应引起结构形变,四个钒原子的磁矩依次为1.31 μB、1.019 μB、1.137 μB和1.335 μB,数值偏离对称性较大。表2中总磁矩接近整数是由于钒的磁矩部分被C7N2H6和C8N4H6分子上反向排列的磁矩所抵消。
为了进一步探究三明治结构的磁性,图4给出了Vm(C7N2H6)n 2-5层团簇的基态上下自旋的总电子态密度(DOS)和分波电子态密度(LDOS)。从DOS图我们可以看到在费米面附近态密度不为零,说明团簇整体呈半金属或金属性质,这种情况和苯夹钒原子三明治团簇结构和苯钒一维无限长纳米线呈半金属特性一致 [26] [27]。对于V2(C7N2H6)3结构我们可以看到DOS中自旋向上和向下的电子态密度是对称的,这与三层团簇结构的反铁磁基态特征一致。从分波电子态密度PDOS中我们发现在费米面附近,钒原子的贡献最大,其次是碳原子的贡献,而氮原子贡献最小,其中涉及的主要是钒原子的3d轨道以及碳和氮原子的2p轨道。此外,我们发现在费米能级附近钒原子和碳氮原子的态密度有部分重合,这说明在团簇中钒原子和C7N2H6分子有较强的共价相互作用。
4. 结论
本文采用第一性原理计算方法对比研究了VmBzn、Vm(C7N2H6)n、以及Vm(C8N4H6)n (n = 1~4, m = n + 1)三明治团簇的结构和磁学性质。计算结果表明C7N2H6和C8N4H6构成的团簇中极性苯分子呈反铁电排列。随着三明治团簇层数的增加,配体为苯分子的团簇中钒–钒平均间距变化不大,而配体为极性苯分子构成的团簇中钒–钒平均间距明显减小,且C8N4H6形成的团簇中钒–钒平均间距减小的趋势最为明显。这是由于带正电的官能团-NH2和带负电的官能团-CN相互吸引所导致的结果。团簇的结合能均为较大正值,说明团簇具有热力学稳定性。我们还发现Vm(C7N2H6)n和Vm(C8N4H6)n团簇在n = 2,4,5时呈现铁磁基态,而n = 3时为反铁磁基态。电子态密度的结果清晰地显示团簇呈现出半金属或者金属态,其中钒原子的3d轨道以及碳和氮原子的2p轨道在费米能级处具有重要的贡献。
致谢
感谢湖北大学杨辉博士的讨论与交流。
基金项目
本研究得到了国家自然科学基金(批准号:11674087)的资助。