1. 引言
我国在低压配电网地区,采用的是三相四线制,即三根火线、一根中性线。我国居民用电大多是采用单相负荷,即单相线与零线之间承担居民用电负荷,而随着我国经济水平的飞速发展,人民生活水平的日益提高,家用电器越来越复杂化、多样化,这就造成我国居民用电低压台区的三相不平衡现象日益严重 [1]。特别对于农村地区,由于用电用户具有分布范围广、输电线路长、用电不规范等特点,更加加重了我国电网系统的不平衡问题。日常生活中,我们经常用三相平衡度、不平衡度来衡量三相不平衡的程度。因此准确快速简便的计算三相不平衡度是我们日益追求的目标。
三相平衡是指三相电压或电流幅值相等、相位相差120°的对称系统。如果三相幅值不同或者相位不对称,则会出现三相不平衡,并随之带来一系列危害。
目前常用的三相不平衡度计算方法主要分为两大类:一是基于相序分解的三相不平衡度,另一则是基于量测值的三相不平衡度。
国家标准GB/T15543-2008《电能质量三相电压不平衡》 [2] 中用负序电压(电流)的有效值与正序电压(电流)的有效值的比来定义三相不平衡度,与国际电工委员会 [3] 的计算方法相同。这类方法需要得到三相电压(电流)的大小和相位来进行相序分解进而得到正负序以及零序分量。计算较为繁琐,并且在工程应用中,无法用仪表得到三相电压(电流)的相位,因此应用范围较窄。
电气与电子工程师协会(IEEE)用三相相电压定义的PVUR936 [4],PVUR112 [5],美国电气制造商协会(NEMA) [6] 和国际大电网委员会(CIGRE) [7] 用三相线电压有效值定义的LVUR公式和GIGER公式等,此类方法虽然采用三相电压(电流)的有效值进行计算,大大简化了计算量,相应的造成计算结果与国标定义相比误差较大,而且无法计算正负序分量,此外有些方法只适用于没有零序分量的三相三线制系统,应用范围不广泛。基于此,我们急需一种基于相序分解和相电压有效值的计算方法。
本文提出以三相负序分量有效值的平方和三相零序分量有效值的平方和的和与三相正序分量有效值的平方之比用于度量三相不平衡。此种方法使用于我国低压台网地区的三相四线制系统。
电源学会团体标准T/CPSS1001-2018《低压配电网有源不平衡补偿装置》附录B中给出了补偿装置不平衡电流补偿需量计算公式
(1)
根据上式,我们可以定义三相电流不平衡度计算公式如下:
(2)
其中:
为零序电流分量,
为正序电流分量,
为负序电流分量。
负载接线方式分为两种,三角形接线方式和星形接线方式。这里我们只考虑星形接线方式,电机星形接法时因为有中性点(电机一般都是三相对称负载所以一般不引出中性线),具体方法是电机的三相绕组的三条尾线连接在一起,三条头接电源,这时有两种电压等级,即线电压和相电压,且线电压等于相电压的
倍,线电流大小等于相电流大小。
2. 文献回顾
2.1. 基于相序分解的三相不平衡度定义
IEC定义三相电压不平衡度为电压的负序分量与电压的正序分量之比
(3)
(4)
;
。
式中
为旋转算子,
,
,
分别为正序分量、负序分
量和零序分量。
在三相三线制系统中,由于没有零序分量,此方法可以准确表达三相不平衡度,在表示三相分量幅值的大小的同时能够反映正负序电压的相角差值。而在三相四线制系统中,零序分量的存在使得此方法不再使用,且此方法需要进行向量运算,需要得到三相向量的幅值和相位,进而造成计算量大,计算速度慢。而在工程应用中,三相向量的相位不易测得,因此此方法无法推广使用。
IEC [4] 定义电压的负序分量有效值与电压的正序分量有效值之比来计算三相电压不平衡度,其表达式为:
(5)
此方法能反映三相电压幅值的大小,虽然避免了相位运算,但也无法反映出正负序电压的相角差值。
当在三相四线制系统中时,由于含有零序分量,也可以用电压的零序分量与电压的正序分量之比来表示三相不平衡度。即
(6)
2.2. 基于量测值的三相不平衡度定义
在工程应用中,由于基于相序分解的三相不平衡度不适用,许多组织和团体定义了一些三相不平度的近似计算方法。
IEEEStd.936-1987定义电压不平衡度为相电压不平衡率 (PVUR)为最大均方根电压值和最小均方根电压值之差与平均相电压的比值,其表达式
(7)
式中
——三相相电压,
为平均相电压,
。
IEEEStd.112-1991定义电压不平衡度为相电压不平衡率 (PVUR), 即三相相电压和平均相电压值差值最大值与平均相电压的比值,其表达式
(8)
式中
——三相相电压,
为平均相电压,
。
美国电器制造商协会(NEMA)用三相线电压的有效值定义电压不平衡度为线电压不平衡率(LVUR),其表达式
(9)
式中
——三相线电压量测值,
为平均线电压,
。
国际大电网委员会 [8] (以下简称CIGRE)用三相线电压定义电压不平衡度,用符号
表示,其表达式为:
(10)
。
式中,
——三相线电压。
2.3. 两大类方法的改进
在工程应用中,由于无法测得三相相位,故而多采用基于量测值定义的三相不平衡度,这样可以避免进行相位计算进而简化计算过程,加快计算速度;基于相序分解定义的三相不平衡度不唯一,由IEC定义的公式可知,在三相三线制电路系统中没有零序分量中,可用式(1)来衡量三相不平衡度,而在既含有负序分量也含有零序分量的三线四线制中,可用式(1)来表示负序不平衡度,式(2)来表示零序不平衡度,而在衡量三相系统不平衡时采用哪种公式,不一而足。因此有必要对三相不平衡度定义的进行改进。
3. 三相不平衡度定义的改进
根据对称分量法,任何一组不对称的三相向量都可以分解成三组相角不同的对称分量:正序分量、负序分量和零序分量。如图1所示

Figure 1. Schematic diagram of symmetrical component method
图1. 对称分量法示意图
设A相相电压为
,B相相电压为
,C相相电压为
;A相的正序分量为
,其相角为0˚,负序分量为
,其相角为
,零序分量为
,其相角为
。
则三相相电压为:
(11)
则等式两边平方相加得
(12)
即
(13)
式中
为三相相电压的量测值,
为正序、负序和零序分量的量测值。
由上式可知,正序、负序、零序分量的平方和为三相向量的平方和的1/3,而在三相四线制系统中,负序分量和零序分量是引起不平衡的主要原因,本文提出以三相零序分量和负序分量量测值的平方和与三相正序分量量测值的平方之比来定义三相不平衡度。即
(14)
由图2可得三相线电压为
(15)
两边同时平方得到三相线电压有效值的平方为:
(16)
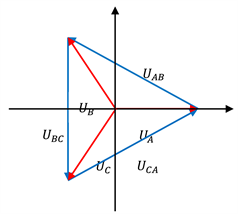
Figure 2. The relationship between three phase voltage and three phase line voltage
图2. 三相相电压与三相线电压的关系
即
(17)
(18)
(19)
式(17)、式(18)、式(19)相加得
(20)
式(17)与式(19)的和与式(18)的2倍相减得到
(21)
式(17)与式(19)相减得到
(22)
整理式(21)(22)得
(23)
(24)
式(23) (24)等式两边同时平方相加得
(25)
整理得
(26)
这里为方便计算,我们令
,
。
显然有
(27)
则
(28)
(29)
则我们有
(30)
(31)
一般的
,可求得
、
联立式(30) (31)整理得
(32)
(33)
由于
,
则
(34)
所以三相不平衡度为
(35)
4. 算例分析
本文用Matlab仿真计算来验证本文所提出的算法的准确性,这里,我们对给定的三组电压的相位和幅值进行计算,如表1所示。计算得出的三相线电压的幅值如表2所示,本文采用公式法、坐标法、LVUR936,PVUR112,LVUR,GIGRE推荐的方法以及本文所提出的方法计算的三相不平衡度结果如表3所示。

Table 1. Three groups of voltage data used in simulation
表1. 仿真所用的3组电压数据

Table 2. Three groups of line voltage data used in simulation
表2. 仿真所用的3组三相线电压的幅值

Table 3. Three phase unbalance degree calculated by different methods
表3. 采用不同方法计算的三相不平衡度
由表3可以看出,本文所提出的方法与公式法和坐标法的计算结果较为接近,具有良好的准确性,但本文提出的方法用零序分量和负序分量的平方和与正序分量的平方作比,不需要三相分量的相位,只需要三相分量的有效值且计算简便,具有较广的应用前景;而相序分解下的定义的三相不平衡度计算复杂、计算量大,当处理大量数据时,计算速度较慢。
本文提出的方法比工程上应用的近似算法更为接近公式法,计算结果更加精确,工程上应用的近似算法没有考虑零序分量,不适于三相四线制系统中,而我国城市和农村居民用电大多是三相四线制系统,因此,这些方法存在误差较大,且应用范围不广的缺点。
5. 总结
本文用三相负序分量和零序分量的平方和与三相正序分量平方和之比来定义三相不平衡度,既避免了相序分解下定义的方法需要三相幅值相位,只需要三相幅值,计算量大为减少,又具有较高的准确性,避免有效值定义下的计算方法的计算误差较大的特点。此外,本文新定义的三相不平衡度适用于存在零序分量的三相四线制系统,因此,本文所提出的计算方法具有更广的应用前景。