博弈论视角下的新冠疫情防控对策分析

Analysis of COVID-19 Epidemic Prevention and Control Countermeasures Based on Game Theory

摘要: 本文针对新冠疫情构建以“地方政府–民众”为参与群体的演化博弈模型，结合实际数据，通过数值分析，得出了与实际情况基本吻合的复制动态方程，分析了各博弈方的策略稳定性和各要素对策略选择的影响。

Abstract: In this paper, an evolutionary game model with “local government-public” as the participating groups was constructed for the COVID-19 epidemic. Based on the actual data and through numerical analysis, a replicative dynamic equation basically consistent with the actual situation was obtained, and the strategic stability of each game party and the influence of various factors on the strategy selection were analyzed.

1. 引言

面对突如其来的新冠肺炎疫情，各个国家、各个地区的应对方式明显不同，因此带来的效果也完全不同。我国在此次疫情防控中展现出来的中国力量、中国精神、中国效率以及负责任的大国形象，得到了国际社会的高度赞誉 [1]。也有些国家置新冠肺炎疫情于不顾，导致疫情越来越严重，当中国举全国之力阻击疫情时，美国在特朗普政府的带领下，对新冠肺炎没有给予足够的重视，反而弱化疫情的存在及危险 [2]。与此同时，为了应对此次疫情导致的经济衰退，各国也出台了很多政策来刺激经济，比如扩大财政支出、减免缓征税费等措施来保障医疗卫生系统，保障民生以及企业生产，还有一系列的宏观经济政策 [3]。在 [4] 中，谢地、王齐以中央政府、地方政府以及民众为参与者，针对抗疫不同阶段分别建立了贝叶斯博弈模型，提出了处罚系数、民众分配系数、中央政府发现地方政府消极抗疫行为的概率等因素会影响抗疫策略的选择。黄婷基于演化博弈理论，研究发现政府的监管和干预行为会对企业产生一定的影响 [5]。

如何有效地控制疫情的蔓延是当务之急，在中央政府的参与下，本文以有限理性的地方政府及民众为参与群体，构建了一个演化博弈模型，分析了各博弈方的策略稳定性和各要素对策略选择的影响，以求找出二者之间的长期利益均衡机制。

2. 演化博弈模型

2.1. 模型假设

假设1：地方政府为参与群体1，民众为参与群体2，地方政府的策略为(监管，不监管) $=\alpha =\left({\alpha }_1,{\alpha }_2\right)$，选择 ${\alpha }_1$ 和 ${\alpha }_2$ 的地方政府的比例分别为 $x$ 和 $\left(1-x\right)$ ；民众的策略为(配合，不配合) $=\beta =\left({\beta }_1,{\beta }_2\right)$，选择 ${\beta }_1$ 和 ${\beta }_2$ 的民众的比例分别为 $y$ 和 $\left(1-y\right)$，其中 $x,y\in \left[0,1\right]$。

假设2：地方政府监管的成本是 $L_1$。地方政府不监管会导致疫情扩散，由此损失的声誉或公信力为 $Z_1$。

假设3：地方政府不监管可以使经济正常运转，地方政府由此带来的额外收益为 $E$。民众不配合、地方政府监管(不监管)时，地方政府的社会经济损失为 $V_1\left(V_2\right)$。

假设4：民众积极配合政府的有关规定，如居家隔离、非必要不外出等造成的经济损失记为 $L_2$。如果一些民众不配合政府部门有关规定，受到的处罚记为 $P$。民众不配合政府的抗疫政策，患上新冠肺炎的治疗费用及身心健康的损失为 $N$，患病概率为 $\mu ,\mu \in \left[0,1\right]$。

2.2. 中央政府参与下的主要参数及模型构建

$\eta$ 是中央政府督察时，地方政府被抽查到的概率， $\eta \in \left[0,1\right]$。 $F$ 是中央政府给予地方政府的防疫专项补助资金。 $\zeta$ 代表地方政府将防疫专项补助资金拨付给民众的比例。地方政府不监管需要退还防疫专项补助资金，并受到政治处罚。中央政府对地方政府的处罚系数为 $\theta$，处罚数额与地方政府的额外收入E相关，中央政府会对罚款进行分配：一部分分配给民众，民众分配系数 $\kappa$。根据以上假设，地方政府和民众的策略博弈矩阵，如表1所示。

Table 1. Evolutionary game benefit matrix of local government-public

表1. 地方政府–民众演化博弈得益矩阵

为了简化运算过程，令：

$a=-L_1+\left(1-\zeta \right)\eta F-V_1+P-\left(1-\theta \eta \right)E+Z_1+V_2$，

$b=-V_1+P+V_2$，

$c=-L_1-V_1+P-E+Z_1+V_2$。

地方政府选择“监管”和“不监管”的期望收益分别为：

$U_{11}=y\left[-L_1+\left(1-\zeta \right)F\right]+\left(1-y\right)\left[-L_1+\left(1-\zeta \right)F-V_1+P\right]$，

$U_{12}=y\left[\left(1-\eta \right)\left(1-\zeta \right)F+\left(1-\theta \eta \right)E-Z_1\right]+\left(1-y\right)\left[\left(1-\eta \right)\left(1-\zeta \right)F+\left(1-\theta \eta \right)E-Z_1-V_2\right]$。

地方政府进行策略选择时的平均支付为：

$\overline{U_1}=x{U}_{11}+\left(1-x\right)U_{12}$。

复制动态方程为：

$C\left(x\right)=\frac{\text{d}x}{\text{d}t}=x\left(U_{11}-\overline{U_1}\right)=x\left(1-x\right)\left[-L_1+\left(1-\zeta \right)\eta F-V_1+P-y\left(-V_1+P+V_2\right)-\left(1-\theta \eta \right)E+Z_1+V_2\right]$。

民众选择“配合”和“不配合”的期望效用分别为：

$U_{21}=x\left(\zeta F-L_2\right)+\left(1-x\right)\left(\zeta F-L_2+\eta \kappa \theta E\right)$，

$U_{22}=x\left(\zeta F-P-\mu N\right)+\left(1-x\right)\left(\zeta F+\eta \kappa \theta E-\mu N\right)$。

民众进行策略选择时的平均支付为：

$\overline{U_2}=y{U}_{21}+\left(1-y\right)U_{22}$。

复制动态方程为：

$C\left(y\right)=\frac{\text{d}y}{\text{d}t}=y\left(U_{21}-\overline{U_2}\right)=y\left(1-y\right)\left(-L_2+xP+\mu N\right)$。

3. 演化博弈模型分析

3.1. 稳定性分析

地方政府、民众之间的策略选择是相互影响的，各群体会通过观察群体内部的其他成员的行为对策略不断进行调整，以期得到最大期望收益。

1) 地方政府的演化稳定策略

令 $N\left(y\right)=a-by$，地方政府选择监管时的稳定状态满足： $C\left(x\right)=0$ 且 $\frac{\text{d}\left(C\left(x\right)\right)}{\text{d}x}<0$。由于

$\partial N\left(y\right)/\partial y<0$，故 $N\left(y\right)$ 关于 $y$ 是减函数。

(1) 当 $y=a/b$ 时， $N\left(y\right)=0$， $\text{d}\left(C\left(x\right)\right)/\text{d}x\equiv 0$， $C\left(x\right)\equiv 0$，此时所有的 $x$ 都处于稳定状态，也就是选择“监管”策略的地方政府的数量不会随时间改变。

(2) 当 $y\ne a/b$ 时，复制动态方程在 $x=0$ 或 $x=1$ 处于稳定状态，即地方政府选择的策略会稳定在“监管”策略或“不监管”策略上。

当 $0<a/b<y<1$ 时， $N\left(y\right)<0$，这时 ${\text{d}\left(C\left(x\right)\right)/\text{d}x|}_{x=0}<0$， $x=0$ 为演化稳定策略，即“不监管”为地方政府的演化稳定策略。

当 $0<y<a/b<1$ 时， $N\left(y\right)>0$，这时 ${\text{d}\left(C\left(x\right)\right)/\text{d}x|}_{x=1}<0$， $x=1$ 为演化稳定策略，即“监管”为地方政府的演化稳定策略。

因为 $\frac{a}{b}=\frac{-L_1+\left(1-\zeta \right)\eta F-V_1+P-\left(1-\theta \eta \right)E+Z_1+V_2}{-V_1+P+V_2}$，所以地方政府用于监管的成本 较低，同时中

央政府给予的防疫专项补助资金 $\left(1-\zeta \right)F$ 较大，这样就可以分担地方政府的一部分财务压力。若地方政府选择“不监管”策略时，其声誉或公信力的损失 $Z_1$ 及中央政府对其的处罚系数 $\theta$ 足够大，同时额外收入 越低，这时有 $0<y<a/b<1$，“监管”则为地方政府的演化稳定策略，即地方政府倾向于从“不监管”策略转向“监管”策略。否则地方政府倾向于从“监管”策略转向“不监管”策略。

2) 民众的演化稳定策略

令 $Q\left(x\right)=\mu N-L_2+xP$，民众选择配合的概率处于稳定状态必须满足： $C\left(y\right)=0$ 且 $\text{d}\left(C\left(y\right)\right)/\text{d}y<0$。由于 $\partial Q\left(x\right)/\partial x>0$，故 $Q\left(x\right)$ 关于 $x$ 是增函数。

(1) 当 $x=\left(L_2-\mu N\right)/P$ 时， $Q\left(x\right)=0$， $\text{d}\left(C\left(y\right)\right)/\text{d}y\equiv 0$， $C\left(y\right)\equiv 0$，此时所有的 $y$ 都处于稳定状态，也就是选择“配合”策略的民众的数量不会随时间改变。

(2) 当 $x\ne \left(L_2-\mu N\right)/P$ 时，复制动态方程在 $y=0$ 或 $y=1$ 处于稳定状态，即民众选择的策略会稳定在“配合”策略或“不配合”策略上。

当 $0<x<\left(L_2-\mu N\right)/P<1$ 时， $Q\left(x\right)<0$，这时 ${\text{d}\left(C\left(y\right)\right)/\text{d}y|}_{y=0}<0$， $y=0$ 为演化稳定策略，即“不配合”为民众的演化稳定策略。

当 $0<\left(L_2-\mu N\right)/P<x<1$ 时， $Q\left(x\right)>0$，这时 ${\text{d}\left(C\left(y\right)\right)/\text{d}y|}_{y=1}<0$， $y=1$ 为演化稳定策略，即“配合”为民众的演化稳定策略。

当民众配合时的经济损失 $L_2$ 越小，由于不配合国家政策而感染新冠肺炎的损失 $\mu N$ 以及处罚 $P$ 越大，这时有 $0<\left(L_2-\mu N\right)/P<x<1$，“配合”为民众的演化稳定策略，即民众倾向于从“不配合”策略转向“配合”策略。否则，民众倾向于从“配合”策略转向“不配合”策略。

3.2. 演化博弈系统平衡点稳定性分析

多群体演化博弈复制动态系统的渐近稳定解一定是严格纳什均衡，严格纳什均衡一定是纯策略，本文主要阐述抗疫过程中各个群体的协调配合以实现抗疫的胜利，因此主要分析{监管，配合}策略的稳定性。

根据各群体的复制动态方程，得到的雅可比矩阵为

$J=\left[\begin{array}{cc}\partial C\left(x\right)/x& \partial C\left(x\right)/y\\ \partial C\left(y\right)/x& \partial C\left(y\right)/x\end{array}\right]$。

将 $x=1$， $y=1$ 代入上式，进而得到其对应的雅可比矩阵。 $\left(1,1\right)$ 是稳定点需满足以下条件：

$\{\begin{array}{c}b-a<0\\ L_2-P-\mu N<0\end{array}$。

此时地方政府、民众倾向于采取{监管，配合}策略。

(1) 地方政府采取“监管”策略的影响因素

当 $b-a<0$，即 $L_1-\left(1-\zeta \right)\eta F<Z_1-\left(1-\theta \eta \right)E$，所以当地方政府不监管时损失的公信力 $Z_1$ 、额外收益 $\left(1-\theta \eta \right)E$ 之差远远大于其监管成本 $L_1$ 、中央政府给予的补贴 $\left(1-\zeta \right)\eta F$，也就是地方政府监管时的成本小于其不监管时损失，地方政府更倾向于选择“监管”策略。

(2) 民众选择“配合”策略的影响因素

当 $L_2<P+\mu N$，即民众配合国家的政策所付出的成本 $L_2$ 远比罚款 $P$ 以及感染新冠肺炎的费用 $\mu N$ 小，民众会更倾向于选择“配合”策略。

4. 数值分析

为了更加直观准确的对各博弈方的策略选择进行稳定性分析，下面用MATLAB R2014b进行数值分析(本文以美元为计量单位，以月为单位)。

我们对武汉的数据¹进行收集，得到的值为：民众配合的经济损失L₂ 按2019年人均GDP来计算为0.0855万，民众患病的费用N为0.3225万，民众不配合的处罚P为4万，中央拨付给武汉的防疫专项补助资金F为93000万，武汉的患病概率μ 为0.00119063，通过对比2020年第二季度与2019年第四季度武汉的GDP，可得V₁ 为14173900万，V₂ 为20000000 (武汉积极抗疫，故此值为假设值)，假设L₁ = 243 万，Z₁ = 5,000,000 万，κ = 0.9，η = 1，E = 5000万，θ = 0.5，ζ = 0.1。

分别将以上数值代入复制动态方程发现，地方政府的复制动态方程不符合实际，故我们对其进行改造，分别使其变为

$\begin{array}{l}{C}^{\ast }\left(x\right)=\frac{1}{8000000}\frac{\text{d}x}{\text{d}t}=\frac{1}{8000000}x\left(U_{11}-\overline{U_1}\right)\\ =\frac{1}{8000000}x\left(1-x\right)\left[-L_1+\left(1-\zeta \right)\eta F-V_1+P-y\left(-V_1+P+V_2\right)-\left(1-\theta \eta \right)E+Z_1+V_2\right]\end{array}$，

$C^{\ast }\left(y\right)=\frac{\text{d}y}{\text{d}t}=y\left(U_{21}-\overline{U_2}\right)=y\left(1-y\right)\left(\mu N-L_2+xP\right)$。

Table 2. The rate of change of Wuhan and public

表2. 武汉、民众的变化率

将得到的数据分别带入不同的新的复制动态方程，即将武汉的数据代入 $C^{\ast }\left(x\right)$， $C^{\ast }\left(y\right)$，可以得到表2，发现方程经改造后更接近实际数值。

接下来将采集到的数据带入新方程，可以看到各博弈方的策略选择随时间的动态变化趋势分别如图1、图2所示。其中，横坐标代表各博弈群体的变化率，纵坐标代表时间。

观察图1发现，地方政府“监管”策略的概率随着时间的推移最终收敛到1。即慢慢地方政府发现“监管”的收益要远远高于“不监管”的收益，这时不监管的地方政府也倾向于选择收益更多的策略，即“监管”策略。

图2表明大部分民众最终会收敛到“配合”策略，但也有极少一部分民众抱侥幸心理，认为自己感染新冠肺炎的概率较低，会选择去工作或是外出游玩，会选择“不配合”策略。

同时由图2可以看出，武汉大部分人民不到“4”的时候就迅速选择了“配合”策略，从而使得疫情在较短的时间内得到了有效的控制，我国民众为避免新冠肺炎疫情的大范围扩散做出了巨大的牺牲。

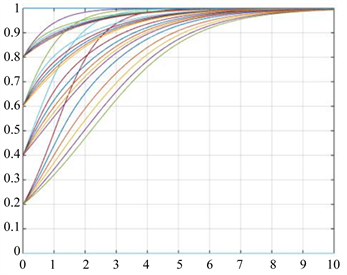
Figure 1. Changes in tactics by local governments

图1. 地方政府的策略变化图

Figure 2. Changes in tactics by public

图2. 民众策略变化图

5. 结论

由地方政府的复制动态方程可知，地方政府为了防止公信力的损失以及来自中央政府的处罚，地方政府应该积极监管民众配合抗疫的行为。中央政府应将地方政府不监管时的处罚系数调高，使得地方政府的收益远远小于被罚的金额，同时当中央政府给予的防疫专项补助资金越多，不监管时的额外收入、地方政府的监管成本越低，这样地方政府会提高选择“监管”的概率。

由民众的复制动态方程可知，当民众不配合国家政策而感染新冠肺炎的损失以及处罚越大，而配合时的经济损失越小，民众为了自身利益就会提高选择“配合”的概率。

我们可以看到当满足设定的条件时，地方政府、民众会收敛于(监管，配合)，即其是系统的演化稳定策略，最终各博弈方会稳定于此状态。

新冠肺炎疫情是一场没有硝烟的战争，在此次战役中可以发现，各国政府、人民在此次危机中的处理方式大有不同，我国在中国共产党的领导下，上下同心积极抗疫，国家更是不计成本的全力救治新冠患者，人民群众也积极响应国家号召居家隔离，做到了不随意外出，外出必戴口罩。在此次战役中全世界都看到了我们国家不仅实力更加强盛，也看到了社会主义的优越性是其他制度所无法比拟的；而反观其他国家，政府推卸责任，民众上街抗议要求复工，全然不看重新冠肺炎疫情，致使全球新冠肺炎疫情确诊人数已经超过1亿人。在危机面前才能展现出个人的思想深度和国家的治理能力以及治理理念等，此次战役更是向世界宣示，在中国共产党的带领下，中国人不惧怕任何挑战！

致谢

本论文是在我的研究生导师侯吉成教授的精心指导下完成的，侯老师不仅向我传授“为学之道”，更教我“为人之本”，他的睿智与高屋建瓴，使我受益匪浅。侯老师丰富的科研经验和严谨的治学之道，潜移默化的影响了我。在本论文的写作过程中，侯老师的全力支持、严格要求和悉心指导，使本论文最终得以完成。为了指导我撰写论文，侯老师花费了大量的时间和精力，在此，谨向侯老师表示由衷的谢意。

NOTES

^*通讯作者。

¹数据来源为各国国家统计局，新浪网，百度，腾讯网，知乎。