加密数字货币市场与美国股票市场联动性研究

Research on the linkage between the Cryptocurrency Market and the U.S. Stock Market

摘要: 为探究加密数字货币市场和美国股票市场之间是否存在一定的相关性并对某些事件表现出相同的反应，本文以2016年1月5日到2021年2月5日纽交所比特币指数(NYXBT)和美国标普500指数(S&P500)数据为样本，建立t-Copula-GARCH-Skewed-T模型对加密数字货币市场和美国股票市场间的联动性进行了研究。结果发现：样本研究期内，加密数字货币市场和美国股票市场的相关性显著增强，并在事件发生前后呈现出类似的变化趋势。结合相关事件进行分析，本文认为政策的放松、中美贸易摩擦、新冠疫情爆发等特定事件通过影响投资者情绪，从而影响加密数字货币市场和美国股票市场的联动性，且样本研究期内新冠疫情的爆发对两市场间联动性波动的影响最大。

Abstract: Based on t-Copula-GARCH-Skewed-T model, we selected the NYSE Bitcoin Index (NYXBT) and the US S&P500 Index (S&P500) price-day transaction data from January 5th, 2016 to February 5th, 2021 as samples and measured the linkage between the cryptocurrency market and the U.S. stock market. The results show that the correlation between these two markets during this period was signifi-cantly enhanced and there existed obvious characteristics of periodic fluctuation. Meanwhile, it is found that there existed connections between certain events and dynamic conditional correlation. Specific events such as policy relaxation, Sino-US trade frictions, and the outbreak of COVID-19 tend to influence the linkage between the cryptocurrency market and the US stock market by affecting investor sentiment. It is shown that during the sample-studied period, the outbreak of COVID-19 had the greatest impact on the linkage between two markets.

1. 引言

2008年，一篇名为《比特币：一种点对点式的电子现金系统》 [1] 的文章标志着比特币的问世。此后十余年内，基于比特币思想、区块链技术的加密数字货币市场迅速发展。作为金融市场中的“新生儿”，加密数字货币市场一直受到各国政府、投资者和研究学者的密切关注。2020年第一季度，新冠疫情爆发，美股经历“断崖式下跌”并多次触发熔断机制；而在2020年3月12日，加密数字货币市场遭遇“黑色星期四”，比特币、莱特币等价格暴跌。那么二者之间是否存在一定的相关性，使两市场对于某些事件表现出相同的反应呢？

本文研究加密货币市场与美国股票市场之间的联动性，并结合特定事件对动态条件相关系数的估计结果进行解释，旨在探寻两市场间波动性的变化规律，为各国政府及投资者提出合理的监管和投资建议。

2. 文献综述

对金融资产收益率序列的波动过程的研究，最早可追溯到上世纪八十年代。Engel [2] 的ARCH模型可用于刻画和预测收益率序列的条件方差。Bollerslev [3] 首次提出GARCH模型，该模型解决了在实际建模中使用ARCH模型时可能需要高阶滞后项的问题。Engel [4] 提出了DCC-GARCH模型描述金融序列之间波动的时变性。为摆脱正态分布假设的约束，由Sklar提出的Copula理论得到了广泛应用。Patton [5] 基于Copula理论发现，相比起贬值时，美元升值时德国马克与美元及日元与美元的相关性更大；张尧庭 [6] 探究了Copula函数在金融领域的可行性；韦艳华等人多次运用Copula理论对中国股票市场的相依性进行分析 [7] [8] [9]；Riadh等人 [10] 使用多种Copula模型建立“金砖四国”(巴西、俄罗斯、印度和中国)股票市场与美股市场之间的动态条件相依结构。而Copula-GARCH模型将Copula模型的灵活性与金融序列的GARCH效应相结合，可以很好地度量市场间的相依性 [11]。李红权等人 [12] 通过Copula-DCC-GARCH模型考察了中国股票市场的国际影响力。

关于加密数字货币的研究主要可以归为三类。第一，对于加密数字货币自身属性及特征的研究。以比特币、以太币为首的数字加密货币均存在较高的市场风险 [13]，而影响比特币价格的主要因素是其交易和投机动机 [14]。由于数字货币市场的“野蛮生长”，相关部门必须对其严格监管 [15] [16]。第二，对于构建投资组合时加密数字货币的对冲性的研究。Dyhrberg [17] 提出比特币对FTSE指数(Financial Times Stock Exchange Index)具有明显对冲能力，对美元的对冲能力仅在短期内体现。Demir等人 [18] 认为比特币在牛市时期可以对冲经济政策带来的不确定性。Conlon等人 [19] 则结合COVID-19疫情背景，提出比特币并不是抵御市场风险的避风港。第三，对于加密数字货币与金融市场的联动性的研究。徐黎明等人 [20] 提出中美比特币市场间的溢出效应是双向的。Corbet等人 [21] 研究发现加密货币独立于传统金融资产价格的波动，Roman Matkovskyy等人 [22] 研究了从金融市场到数字货币市场的传染效应。曾萤等人 [23] 的研究反映出加密数字货币市场与传统金融市场之间的动态关联性弱于传统金融市场之间的关联性。

基于对上述文献的总结分析，笔者发现既有研究中，鲜有学者结合重大事件分析数字货币市场与传统金融市场之间联动性，且研究方向尚未涉及两市场间的联动性波动特征。在有关数字货币与其他金融资产相关性的现有研究之中，相较于GARCH模型，Copula-GARCH模型的应用较少。同时，对于加密数字货币的研究存在较多结论不统一的现象。如Dyhrberg [24] 认为比特币与黄金和美元有很大的相似性，其属性介于黄金和美元之间；而Corbet等人 [21] 尽管使用与Dyhrberg完全相同的数据样本及经济学模型进行“复制研究”，但得出了比特币与黄金和美元全然不同的结论。

本文的主要贡献在于：第一，运用时变t-Copula-GARCH-Skewed-T模型研究了加密数字货币市场和美国股票市场间的动态联动性，实现了对变量间非线性、非对称性相依关系的描述；第二，本文使用2016年1月5日至2021年2月5日的最新数据进行研究，可以反映出两大金融市场的最新变化，此外，在样本时间段内加密数字货币市场已步入稳定发展的状态，更具有研究价值和说服力；第三，结合本文研究结论对各国监管者及投资者提出了合理建议，具有一定现实意义。

3. 模型构造

3.1. Copula函数

根据Sklar定理，任何一个联合分布函数都可由边缘分布函数和Copula函数构成，且如果所有的边缘分布函数均连续，则可以确定唯一的Copula函数。由于Copula函数具有将联合分布函数与边缘分布函数相连接的作用，故被称为连接函数，该函数可用于描述两个随机变量之间的相依结构。

3.2. 边缘分布函数

金融时间序列的显著特征之一是存在条件异方差。由于异方差可能使t检验结果及模型的预测产生不良影响，故需先消除异方差。为此，Engel [2] 提出自回归条件异方差模型(ARCH模型)。在此基础上，Bollerslev [3] 为提高模型的实用性，提出广义自回归条件异方差模型(GARCH模型)。

基本的GARCH(p,q)模型表示如下：

均值方程：

$r_t=c+\underset{i=1}{\overset{p}{{\displaystyle \sum }}}{\phi }_i{r}_{t-i}+{\epsilon }_t$ (1)

方差方程：

${\sigma }_t^2={\alpha }_0+\underset{i=1}{\overset{p}{{\displaystyle \sum }}}{\alpha }_i{\epsilon }_{t-i}^2+\underset{j=1}{\overset{q}{{\displaystyle \sum }}}{\beta }_j{\sigma }_{t-j}^2$ (2)

其中， $r_t$ 表示资产收益率， ${\epsilon }_t$ 表示随机误差项。 ${\sigma }_t^2$ 表示t时刻 ${\epsilon }_t$ 的条件方差，对于给定的随机变量 ${\epsilon }_{t-1}^2,{\epsilon }_{t-2}^2,\cdots ,{\epsilon }_{t-p}^2$，有 ${\sigma }_t^2=E\left({\epsilon }_t/{\epsilon }_{t-1}^2,{\epsilon }_{t-2}^2,\cdots ,{\epsilon }_{t-p}^2\right)$。 ${\alpha }_i$ 和 ${\beta }_j$ 为待估计参数。

由于金融时间序列的条件分布常出现高峰厚尾、偏斜等特征，不满足正态分布假设，而t分布、Skewed-T分布等可以更加合理地描述金融序列。由于比特币和S&P500的收益率序列均向左偏斜，而Skewed-T分布模型(Bruce E. Hansen)可以准确拟合偏态分布时间序列数据，故本文选用该分布。其密度函数如下式所示：

$\text{Skewed-T}\left(z|\eta ,\Phi \right)=\{\begin{array}{l}bc{\left[1+\frac{1}{\eta -2}{\left(\frac{bz+a}{1-\Phi }\right)}^2\right]}^{-\eta +\frac{1}{2}},z<-\frac{a}{b}\\ bc{\left[1+\frac{1}{\eta -2}{\left(\frac{bz+a}{1+\Phi }\right)}^2\right]}^{-\eta +\frac{1}{2}},z\ge -\frac{a}{b}\end{array}$ (3)

其中， $a=4\Phi c\frac{\eta -2}{\eta -1},b=1+3{\Phi }^2-a^2,c=\frac{\Gamma \left(\eta +\frac{1}{2}\right)}{\sqrt{\pi \left(\eta -2\right)}\Gamma \left(\frac{\eta }{2}\right)}$ ； $\eta$ 为函数的峰度参数，其取值范围为 $2<\eta <\infty$ ；

$\Phi$ 为函数的不对称参数，其取值范围为 $-1<\Phi <1$。

3.3. 动态条件相依结构

Copula模型可以用来进行金融市场联动性分析。本文选用Student-Copula (t-Copula)、Gaussian-Copula、Clayton-Copula和SJC-Copula四个模型拟合加密数字货币和美国股票市场相依关系，依据AIC和Log Likelihood准则，t-Copula的拟合效果最好。因此，本文运用参数时变的二元动态t-Copula来描述股票市场和加密数字货币市场之间的动态非线性相依性，函数模型介绍如下。

自由度为v的二元时变t-Copula函数的分布函数和密度函数分布为：

$C\left(u,\upsilon ;\rho ,v\right)={\displaystyle {\int }_{-\infty }^{T_v^{-1}\left(u\right)}{\displaystyle {\int }_{-\infty }^{T_v^{-1}\left(\upsilon \right)}\frac{1}{2\pi \sqrt{1-{\rho }^2}}\cdot {\left[1+\frac{r^2+s^2-2\rho rs}{v\left(1-{\rho }^2\right)}\right]}^{-\frac{v+2}{2}}\text{d}r\text{d}s}}$ (4)

$c\left(u,\upsilon ;\rho ,v\right)={\rho }^{-\frac{1}{2}}\frac{\Gamma \left(\frac{v+2}{2}\right)\Gamma \left(\frac{v}{2}\right)}{{\left[\Gamma \left(\frac{v+1}{2}\right)\right]}^2}\frac{{\left\{1+\frac{{\left[T_v^{-1}\left(u\right)\right]}^2+{\left[T_v^{-1}\left(\upsilon \right)\right]}^2-2\rho T_v^{-1}\left(u\right)T_v^{-1}\left(\upsilon \right)}{v\left(1-{\rho }^2\right)}\right\}}^{-\frac{v+2}{2}}}{{{\displaystyle \prod }}_{i=2}^2{\left\{1+\frac{{\left[T_v^{-1}(\cdot )\right]}^2}{v}\right\}}^{-\frac{v+2}{2}}}$ (5)

其中 $u,\upsilon$ 是随机变量， $\rho$ 是相关系数， $T_v^{-1}(\cdot )$ 是自由度为v的t-Copula函数的逆函数。

时变t-Copula函数自身尾部较厚，因而对随机变量尾部的相关变化较敏感，故针对金融序列的偏斜、峰尖尾厚等特征有较好的适用性 [25] [26]；同时该函数也可以刻画出变量间相关关系的对称特点，即无论是增大或减小，变量的变化趋势总是对称的。

3.4. 时变t-Copula-GARCH(1,1)-Skewed-T模型参数估计

设随机变量 $R_{\text{cryptocurrency}}$ 和 $R_{\text{stock}}$，其边缘分布分别为 $F\left(R_{\text{cryptocurrency}};{\theta }_1\right)$ 和 $G\left(R_{\text{stock}};{\theta }_2\right)$，边缘分布密度函数为 $f\left(R_{\text{cryptocurrency}};{\theta }_1\right)$ 和 $g\left(R_{\text{stock}};{\theta }_2\right)$， ${\theta }_1$ 和 ${\theta }_2$ 为未知参数。

设Copula分布函数为 $C\left(u_1,u_2;\lambda \right)$，其中 $\lambda$ 为函数中的未知参数。

则Copula的密度函数为：

$c\left(u_1,u_2;\lambda \right)=\frac{{\partial }^{2}C\left(u_1,u_2;\lambda \right)}{\partial u_1\partial u_2}$ (6)

故 $R_{\text{cryptocurrency}}$ 和 $R_{\text{stock}}$ 的联合分布函数为：

$C\left(F\left(R_{\text{cryptocurrency}};{\theta }_1\right),G\left(R_{\text{stock}};{\theta }_2\right);\lambda \right)$ (7)

联合密度函数为：

$\begin{array}{c}c\left(F\left(R_{\text{cryptocurrency}};{\theta }_1\right),G\left(R_{\text{stock}};{\theta }_2\right);\lambda \right)\cdot f\left(R_{\text{cryptocurrency}};{\theta }_1\right)g\left(R_{\text{stock}};{\theta }_2\right)\end{array}$ (8)

则收益率序列的似然函数为(n为样本数量)：

$L\left({\theta }_1,{\theta }_2;\lambda \right)={\displaystyle {\prod }_{i=1}^{n}c\left(F\left(R_{\text{cryptocurrency}};{\theta }_1\right),G\left(R_{\text{stock}};{\theta }_2\right);\lambda \right)\cdot f\left(R_{\text{cryptocurrency}};{\theta }_1\right)g\left(R_{\text{stock}};{\theta }_2\right)}$ (9)

等式两边同取对数，得对数似然函数为：

$\ln L\left({\theta }_1,{\theta }_2;\lambda \right)$ (10)

为使对数似然函数中的各参数同时取得最大值，本文使用由Joe提出的边缘分布推断法(IFM估计)。具体分为两步进行，先估计边缘分布，再估计联合分布函数模型的参数。

首先取各金融资产时间序列样本 $z_{i,t}$，分别对其边缘分布函数的参数 ${\theta }_i$ 进行极大似然估计 $\left(i=1,2;t=1,2,\cdots ,T\right)$ ：

${\hat{\theta }}_1=\arg \max \underset{t=1}{\overset{T}{{\displaystyle \sum }}}\ln f\left(z_{1,t};{\theta }_1\right)$ (11)

${\hat{\theta }}_2=\arg \max \underset{t=1}{\overset{T}{{\displaystyle \sum }}}\ln g\left(z_{2,t};{\theta }_2\right)$ (12)

式中 ${\hat{\theta }}_1,{\hat{\theta }}_2$ 分别为参数 ${\theta }_1,{\theta }_2$ 的估计值。将求解的 ${\hat{\theta }}_1,{\hat{\theta }}_2$ 代入似然函数，即可计算出Copula函数的未知参数。

$\hat{\lambda }=\arg \max \underset{t=1}{\overset{T}{{\displaystyle \sum }}}\ln c\left(F\left(R_{\text{cryptocurrency}};{\hat{\theta }}_1\right),G\left(R_{\text{stock}};{\hat{\theta }}_2\right);\lambda \right)$ (13)

4. 样本选取与描述

4.1. 数据选取

本文研究加密数字货币市场与美国股票市场的联动性，并分别选用纽交所比特币指数(NYXBT)和美国标普500指数(S&P500)作为加密数字货币和美国股票市场的代表。选取二者的收盘价格日数据作为研究样本，货币资产指标选择美元指数。随着2016年比特币产量第二次减半，一年之内其价格飙升十倍，此后比特币活跃于金融投资领域中，并持续至今。故选取的时间区间为2016年1月5日至2021年2月5日，数据频度为日度。数据均来源于英为财情(https://cn.investing.com/)。

由于长期以来，比特币的市值一直占据数字货币市场的主导地位，且影响力和市值占比远高于其他数字货币，故将比特币作为加密数字货币的研究代表。而标普500指数S&P500作为美国股票市场三大股票指数之一，相比道琼斯工业指数和纳斯达克100指数，其采样面更广、代表性更强，故本文选用S&P500作为研究样本。

由于两市场之间存在不同的交易日期，故先对市场间不重叠的交易日(如周末、部分节假日股票市场闭市的日期)交易数据进行了剔除，最终得到1261个时序样本。

为保证所研究的时间序列的平稳性，更好地研究价格变化的程度，将日收盘价格均转化为对数收益性时间序列，公式如下：

$r_t=\ln y_t-\ln y_{t-1}$ (14)

其中， $r_t$ 表示对数收益率， $y_t$ 表示日收盘价格数据。

4.2. 样本数据的基本特征

比特币指数和标普500指数的对数收益率如图1和图2所示。根据两图可初步判断出，两市场收益率均具有突变性，且比特币市场收益率及其波动均更大。

Figure 1. Daily returns of Bitcoin (NYXBT)

图1. 比特币收益率序列

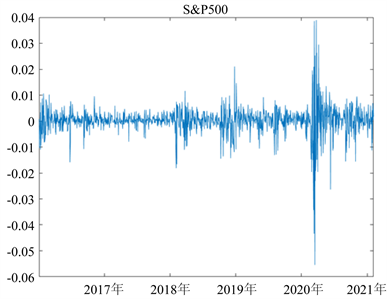
Figure 2. Daily returns of S&P 500 Index (S&P500)

图2. S&P500收益率序列

比特币和S&P500的日收盘价格走势图见图3和图4。从两图中可以初步分析出数字货币市场和美股市场间呈现联动性的变化：2017年比特币发展迅速，价格飙升；同时美股也呈现大幅上涨的趋势。由于政策和监管的影响，2018年数字货币市场持续下跌，而美股市场总体仍呈上涨态势，但两者出现波峰和波谷的时期相近，且近乎同时与2018年底及2019年初急速下跌。随后半年内，二者都开始波动式增长。从2019年6月至2020年2月，数字货币和美股走势相反，但该时间段内出现的波峰和波谷日期相近。在2020年3月12日，比特币遭遇“黑色星期四”，价格暴跌；且美股市场也于该月经历断崖式下跌。随后，两市场又逐渐回暖，价格迅速上涨。

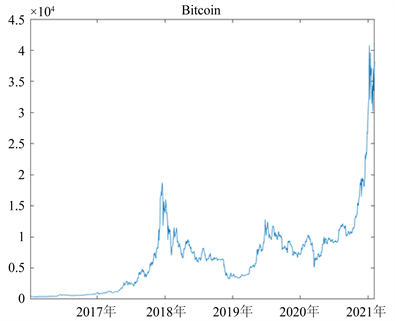
Figure 3. Daily closing price of Bitcoin

图3. 比特币日收盘价格走势图

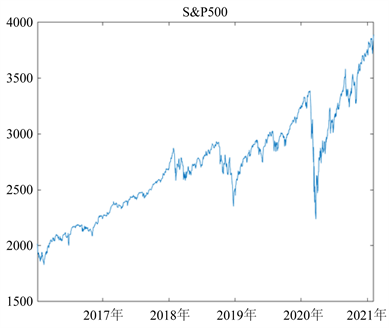
Figure 4. Daily closing price of S&P500

图4. S&P500日收盘价格走势图

通过对价格走势图的简单分析可初步判断出，数字货币市场和美国股票市场周期较一致，二者呈现出联动性特征。

4.3. 数据的统计表述

对比特币和S&P500日收益率序列进行统计性描述，所得结果如表1所示。

Table 1. Descriptive statistics of returns of bitcoin and S&P500

表1. 各日收益率序列的统计描述

注：① 上表中后三行为各项检验的P概率值，使用EVIEWS 10.0计算得出；***、**和*分别表示在1%、5%和10%的水平上显著；② 单位根检验使用“Unit Root Test”进行Augmented Dickey-Fuller检验，原假设为单位根存在(即序列不平稳)；③ 异方差检验使用“Heteroskedasticity Tests”进行ARCH检验，原假设为序列不存在ARCH效应；④自相关检验使用“Serial Correlation LM Test”进行检验，原假设为滞后1阶的序列自相关系数为0 (即序列不存在自相关)。

从上表的统计数据可以看出，比特币的平均日收益率及标准差均高于S&P500，说明比特币市场收益较高、波动较大；同时，比特币最大收益率大于S&P500、最小收益率小于S&P500也说明其收益波动较大。

从偏度来看，两市场收益率均呈左偏趋势，且S&P500市场左偏幅度更大；从峰度来看，两市场收益率均大于3，说明两者分布均呈现尖峰厚尾分布，在1%的置信水平下，不符合正态分布特征；此外，两日收益率序列的JB统计量值均偏大，同样说明两市场的收益率序列拒绝正态分布的假设。

由检验结果可知，在1%显著性水平下，比特币和S&P500的收益率序列均通过单位根检验，故序列平稳，避免了分析中的“伪回归”现象。同时，比特币不存在自相关，但存在异方差；S&P500在1%的置信水平下存在异方差和自相关。

5. 加密数字货币市场与美股市场联动性分析

本文运用前文部分构造的模型进行加密数字货币市场与美股市场联动性实证分析。研究过程如下：第一，对S&P500收益率序列的条件均值建立AR模型，消除其自相关性；第二，由于两收益率序列均存在ARCH效应，故使用GARCH模型分别拟合两序列的条件方差，以消除异方差性；最后，通过比较各类Copula函数的拟合程度来选取合适的模型来分析两市场间的联动性。本文借鉴了Manthos Vogiatzoglou [27] 的动态Copula工具包3.0，并使用MATLAB R2019a软件进行模型计算。具体步骤如下：

首先，通过AR模型对S&P500收益率序列进行拟合，其拟合最优阶数为1阶。

其次，由于样本数据均不服从正态分布，故选择GARCH(1,1)~Skewed-T进行拟合。两收益率序列的边缘分布参数估计结果见表2。

根据表2结果，两序列的AR-GARCH(1,1)-Skewed-T模型中， ${\alpha }_i$ 与 ${\beta }_i$ 之和均小于1，因此模型回归结果稳健。

Table 2. Marginal distribution parameter estimation of bitcoin and S&P500

表2. 比特币和S&P500收益率序列边缘分布参数估计结果

注：上述参数均已通过t检验，即上述表格中的各参数均显著；括号中的数值为标准误差值。

对各序列进行拟合后，对二者进行联动性分析。为了选择能合理且充分对数据进行拟合的模型，本文选用Student-Copula (t-Copula)、Gaussian-Copula、Clayton-Copula和SJC-Copula四个模型对加密数字货币和美国股票市场的对数收益率进行拟合。因为时变t-Copula函数模型的AIC值最小且Log Likelihood检验值最大，所以本文选择该模型对样本数据进行拟合，可以更全面准确地描述加密数字货币与美国股票市场之间的相关关系。

表3列出了t-Copula函数的参数估计结果。系数 $\alpha$ 的估测值非常接近于 0，系数 $\beta$ 的估测值接近于1，而自由度系数 $\nu$ 的估测值大约为20；且在标准误差之下，t-Copula函数的三个系数均在统计上显著。由 $\alpha +\beta <1$ 可知，加密数字货币市场与美股市场的相关性具有长期性，即前一期对本期的相关性有正影响。

Table 3. Parameter estimates of the time-varying t-copula

表3. BTC和S&P500收益率在t-Copula下拟合结果

注：上述参数均已通过t检验，即上述表格中的各参数均显著；括号中的数值为标准误差值。

图5为根据t-Copula-GARCH(1,1)-Skewed-T模型估计出的动态条件相关系数图。

依据动态条件相关系数随时间的变化图，可进行以下分析。

第一，在研究时期内，两市场在2016年3月到9月、2018年2月到3月、2019年2月到6月间较集中地呈现负相依性，在样本时间内的其余时段整体为正相关且相关性系数在0~0.25范围内波动。

第二，根据图5，两市场间的动态条件相关系数在2016年9月9日到2018年3月22日、2018年3月22日到2019年5月6日和2019年5月6日到2021年1月5日单个时间段内呈现出趋同的变化趋势。故本文按照波形图的相似性将样本分为四个阶段，如图6所示。阶段2、3、4内相关性系数的峰值分别为0.09889、0.12613和0.24008，不断增大，说明在样本期间加密数字货币市场和美国股票市场的相关性显著增强。

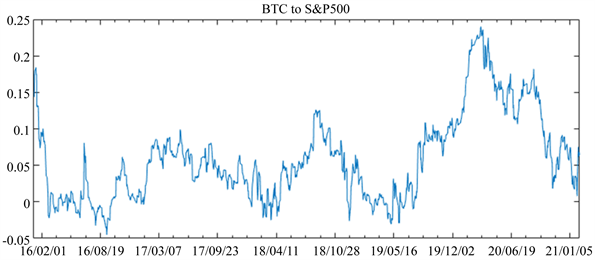
Figure 5. The evolution of dynamic conditional correlation coefficient of Bitcoin and S&P500

图5. 比特币对S&P500的动态条件相关系数

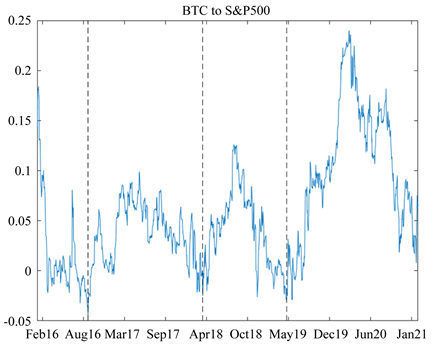注：虚线表示分段日期。本文将样本分为阶段1 (2016/1/5~2016/9/9)、阶段2 (2016/9/9~2018/3/22)、阶段3 (2018/3/22~2019/5/6)和阶段4 (2019/5/6~2021/1/5)

Figure 6. The evolution of dynamic conditional correlation coefficient of Bitcoin and S&P500 (with split stages)

图6. 比特币对S&P500的动态条件相关系数分段图

由于比特币和S&P500收益率序列表现出增强的联动性，表明二者受一些共同因素的影响，对相同事件做出的反应越来越同步，从而价格上呈现出同涨同跌的趋势，且这种趋势不断增强。

阶段2内的相关性系数峰值出现在2017年5月。自2017年初到该峰值出现的时间，比特币和美国股票指数几乎无回调趋势并一直高涨。该年度内，美国政府对加密数字货币整体持积极开放的态度且相关监管政策不严，前美联储主席Jerome H. Powell [28] 还明确表达对比特币等数字货币前景的看好。在此背景下，以比特币为首的各类数字货币繁荣发展并获得了投资者充分的关注。基于对市场的整体把握和预测，投资者在投资一种资产时，通常也会考虑比较、尝试其他金融资产。由于比特币和美股行情持续向好，投资者对金融投资的态度愈发趋于乐观，在市场中的活跃程度得以提升，从而进一步推动两者价格继续上扬，促进两市场间的相关性增强。

阶段3的动态条件相关系数峰值出现在2018年8月，与美国政府对华增加25%关税事件时间相对应。关税的加征不仅未改善美国贸易逆差的情况，而且随着贸易战的升级，美国通货膨胀率增长，普通家庭的年支出增加、美国民众的工作岗位减少。在此背景下，投资者信心指数下降，对投资及市场持消极态度，投资积极性削弱。此外，增加关税、引发贸易摩擦的举措使美国股票市场自身波动加剧，同时也引发了世界经济的不稳定性。在政治、经济不稳定时局之下，投资者的投资力度也极度缩水。因此伴随着中美贸易摩擦，加密数字货币市场与美国股票市场均受到一定冲击，两市场联动性增强、动态条件相关系数增大。

阶段4相关性系数峰值出现在2020年3月，该现象与新冠疫情的爆发密切相关。2020年3月11日，世界卫生组织宣布新冠肺炎疫情已有全球性大流行的趋势。由于新冠疫情期间不确定因素众多，金融序列波动性加强，投资者预测市场趋势的难度增大；同时，新冠疫情对世界各国带来的直接经济损失、对中小企业及普通家庭的损害程度都相当大，投资者用于购买金融资产的自由资金不足。在恐慌、不安定的状态中，投资者自身经济实力减弱，因此对投资的热情和关注度极速降低，将更倾向于将资产进行分配而非大量投资。因此金融市场中的资金流动数量减少、频率降低，加密数字货币市场与美国股票市场均受重创，两市场联动性显著加强。

据以上分析，加密数字货币市场和美国股票市场的联动性针对特定事件表现出一致的变化趋势；特定事件对两市场间联动性变化的传导机制一致，即特定事件通过影响投资者情绪，从而对联动性产生影响。在本文分析的特定事件之中，新冠疫情对加密数字货币市场和美国股票市场的联动性的影响最大。上述事件对加密数字货币市场与美股市场间联动性的影响可总结为图7。

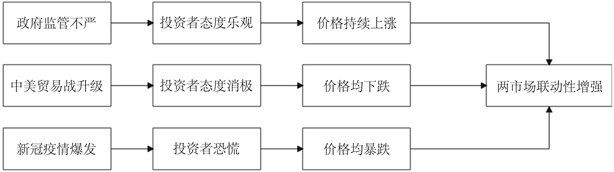
Figure 7. The impacts of specific incidents on the volatility relationship between two markets

图7. 特定事件对两市场间联动性的影响

6. 结论

本文以2016年1月5日到2021年2月5日纽交所比特币指数(NYXBT)和美国标普500指数(S&P500)数据为样本，结合特定事件对加密数字货币市场和美国股票市场间的联动性进行了研究与分析。结果发现：

(1) 以比特币为代表的加密数字货币和以S&P500指数为代表的传统金融资产金融收益率序列均存在尖峰厚尾特征，且加密数字货币的收益率及波动程度更大。通过建立t-Copula-GARCH(1,1)-Skewed-T模型发现，研究期内，加密数字货币市场和美国股票市场相关性显著增强，并在事件发生前后呈现出类似的变化趋势。

(2) 结合相关事件进行分析，本文认为2017年政府监管不严、2018年中美贸易摩擦、2020年新冠疫情爆发等特定事件通过影响投资者情绪，从而影响加密数字货币市场和美国股票市场的联动性。且在2016年到2021年初各大事件的背景下，新冠疫情的爆发对两市场间联动性波动的影响最大。

7. 建议

针对本文的研究结果，提出以下建议。

第一，加强监管力度，注意风险预警。各国政府需寻找有效的监管方法，利用现代科学技术，严格监管加密数字货币市场，从而保证金融市场的安全稳定。同时，由于加密数字货币市场和传统金融市场的联动性易受外部事件的影响，因此相关部门需要实时检测并预测国内外重大事件及形势变化带来的金融风险，从而避免数字货币市场引发传统金融市场的剧烈震荡。

第二，加快建设以中央银行为主导的未来数字货币支付体系。加密数字货币高收益–强波动性、去中心化而不易受政府监管的性质，易使其主要成为投资工具及非法交易媒介。然而，“区块链技术”对数字经济时代意义非凡。因此，我国应尽快完善DC/EP支付体系的建设，在央行的引领、法律的保护之下，充分发挥数字货币反洗钱、反非法交易、降低交易成本的功能，为未来我国经济稳定发展保驾护航。

第三，投资需谨慎。投资者在投资前应充分了解加密数字货币交易的特殊机制，并认识到进行该投资的高风险性。在进行选购时，要通过正规交易平台，在理性分析市场波动趋势的基础上，进行合理的投资。由于加密数字货币市场与传统金融市场之间存在联动关系，且二者针对特定重大事件将做出明显反应，投资者需注意风险防范，提前做好风险管理措施；并掌握市场整体节奏，选择合适的投资周期。

附录

Table A1. Parameter estimates of the time-varying copulas

表A1. 四类时变Copula函数模型拟合情况

Student-Copula、Gaussian-Copula、Clayton-Copula和SJC-Copula模型的拟合情况如上表示。由于student-Copula拟合结果的AIC值最小、Log Likelihood值最大，故选择student-Copula模型作为加密数字货币市场与美国股票市场的动态条件相依结构。