1. 前言和主要结果
本文研究如下Schrödinger-Poisson系统
(1.1)
极小能量变号解的存在性和渐近性态,其中
(
)是一个有界的光滑区域,
是一个大于零的参数,
。
系统(1.1)也来源于经典的Schrödinger-Poisson系统。近年来,一些学者特别关注Schrödinger-Poisson系统变号解问题研究,如文献 [1] - [10]。然而,这些文献都是在泊松函数前的参数大于零的条件下变号解的相关问题。
最近,在文献 [11] 中,Qian研究了如下基尔霍夫方程极小能量变号解
(1.2)
其中
(
)是一个有界光滑区域,
,
,
。运用约束变分,作者首先证明了当
充分小时系统(1.2)基态变号解的存在性;其次,证明了基态变号解的能量值严格大于基态解的能量值;最后,作者讨论了基态变号解的渐近行为。
受上述工作,尤其是文献 [11] 的启发,本文主要讨论系统(1.1)基态变号解的存在性。
设
是标准的Hilbert空间,其上的范数为
。注意到,对任意的
,记
是
在
中的唯一解,且
. (1.3)
把(1.3)带入到系统(1.1)的第一个方程,系统(1.1)可转化为关于u的微分方程,其相应的能量泛函定义为:
显然
,且系统(1.1)的弱解是能量泛函
在
中临界点。
此外,如果
是系统(1.1)的解并且
,则u是系统(1.1)的变号解,此处
,
。
考虑到对于任意的
很难找到一个常数
使得
,其中
。为解决这一困难,定义截断函数
如下:
修正能量泛函
为如下泛函:
,
其中对于任意的
,
。显然,
。
令
,
主要结果如下:
定理1.1存在
,使得对于
系统(1.1)在
中至少有一个基态变号解
,其中
的能量严格大于基态解的能量值。
2. 几个重要引理
引理2.1.
且
,
使得
并且当
足够小时,
。
证明:固定
且
,定义泛函h:
为
(2.1)
因此泛函
。再根据泛函h和
的定义,可得当
时,
。再由泛函h的连续性,可得泛函h在
中存在最大值点
。
下面证明泛函h的最大值点不能在
的边界处取得。不失一般性,假设
是泛函h的最大值点。我们很容易的得到,当
,
且
足够小时
(2.2)
用相同的方法可得
。因此,泛函h的最大值不能在边界处取得,即存在最大值点
满足
。
据此可得
,即
。
根据引理2.1,下面的推论成立。
推论2.1. 对于
,
,
使得
并且当
足够小时,
。
引理2.2. 泛函
是下方有界的且在
上是强制的。
证明:设
,则
,根据p的取值范围,下面分两种情况进行讨论。
1) 当
时:
(2.3)
2) 当
时:
(2.4)
因此,由(2.3)和(2.4)知
是下方有界且强制的。
引理2.3. 令
,则
1) 对于
,
常数
使得
;2) 集合
是闭的。
证明:1) 使用反证法,设
使得
或者
。根据
,
,得到
.
由Sobolev不等式和
,可得到
和
即有
。另一方面,根据
或者
,对于任意的
,很容易得到
.
这是不可能的.因此结论1) 成立。
2) 令
,
。根据
,则
因此,
。
根据1) 中的结论,对于
,可得到
,即
。因此,
。所以,对于
,集合
是闭的。
引理2.4. 存在
和序列
使得对于任意的
有
和
。
证明:根据引理2.2和2.3,对于
,使用Ekeland变分原理得到极小化序列
满足
,且对任意的
有
。显然,
在
中
有界。
如果我们证明了
,则引理2.4证明结束.为了完成证明,对于任意固定的
和任意的
,我们考察如下
泛函
,
.
令
,则
由于
,我们可得到
。此外,有
(2.5)
(2.6)
(2.7)
(2.8)
根据引理2.3的1),对于任意的
,可得到
(2.9)
结合(2.5)~(2.9)和
的有界性,取充分小的
,使得对于任意的
有
.
因此,根据隐函数定理得到
且两个一阶可导泛函
,使得
和
,
. (2.10)
即
,
。
令
,则
,
. (2.11)
根据泰勒展开式,
,从而有
.
根据(2.11),则
. (2.12)
结合(2.5),(2.9)和
的有界性,我们容易得到存在
使得对于任意的
,有
。类似地,我们可得到对于任意的
有
。
下面固定n,令(2.12)中的
,可得到
。
因此,
。所以
。这样我们完成了引理2.4的证明。
根据引理2.2和引理2.3,我们得到
。
引理2.5. 如果
,则
满足
条件。
证明:令
且是
的
序列,即
,
. (2.13)
根据引理2.2可得到
在
中是有界的,因此,存在
满足
,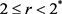 . (2.14)
. (2.14)
根据(2.13)和(2.14),对于足够大的n,我们有
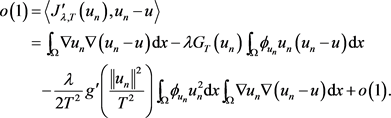 (2.15)
(2.15)
对于任意的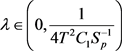 ,也可得到
,也可得到
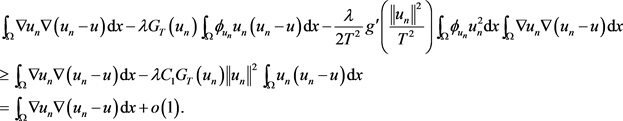
因此,根据(2.15)可得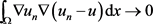 ,即
,即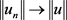 。又
。又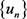 在
在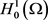 中弱收敛,便可得
中弱收敛,便可得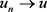 。
。
引理2.6.取引理2.4中的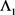 ,则对于任意的
,则对于任意的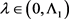 ,存在
,存在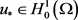 使得
使得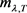 在
在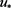 处可达,且
处可达,且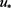 是泛函
是泛函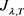 的变号临界点。
的变号临界点。
证明:根据引理2.4,存在极小化序列 使得对于
使得对于 ,有
,有
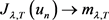 和
和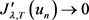 。
。
根据引理2.5,存在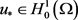 使得在
使得在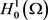 中,
中,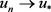 。结合引理2.3,可得到
。结合引理2.3,可得到 ,
,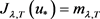 ,
,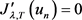 ,即
,即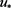 是
是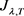 的变号临界点且
的变号临界点且 。
。
引理2.7. 令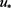 是引理2.6中泛函
是引理2.6中泛函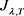 的变号临界点,则当T足够大时,存在
的变号临界点,则当T足够大时,存在 使得对于任意的
使得对于任意的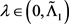 有
有 。
。
证明:定义泛函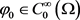 ,
,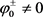 .根据引理2.1,存在
.根据引理2.1,存在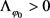 且
且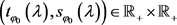 使得
使得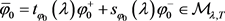 成立,此处的
成立,此处的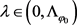 。则可得到
。则可得到
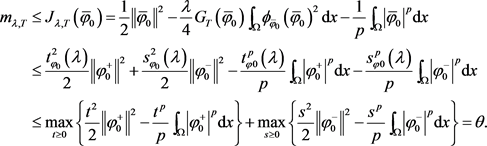 (2.16)
(2.16)
此处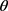 是一个常数,独立于
是一个常数,独立于 ,T。下面将对p分两种情况进行讨论:
,T。下面将对p分两种情况进行讨论:
情况一: 时,在此情况下,与引理2.2的证明类似,由
时,在此情况下,与引理2.2的证明类似,由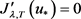 得
得
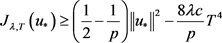 . (2.17)
. (2.17)
假设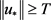 ,则根据(2.16),(2.17)得
,则根据(2.16),(2.17)得
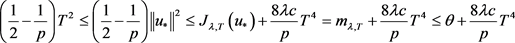 .
.
当T足够大和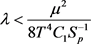 时,得出矛盾。
时,得出矛盾。
情况二: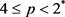 时,与引理2.2证明相同,根据
时,与引理2.2证明相同,根据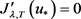 ,可得
,可得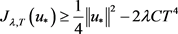 。因此,对于足够大的T,当
。因此,对于足够大的T,当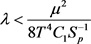 时,得到与情况一相同的结论。这与假设是矛盾的。所以,令
时,得到与情况一相同的结论。这与假设是矛盾的。所以,令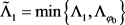 ,当
,当 时结论成立。
时结论成立。
3. 主要结果的证明
定理1.1将分三步来进行证明:
第一步:存在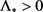 使得对于任意的
使得对于任意的 ,系统(1.1)有基态变号解。
,系统(1.1)有基态变号解。
取引理2.7中的T, ,根据引理2.6和2.7我们可得到
,根据引理2.6和2.7我们可得到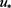 是
是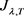 的变号临界点且满足
的变号临界点且满足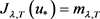 和
和 。再结合
。再结合 得
得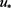 是
是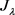 的变号临界点且满足
的变号临界点且满足 。为了证明我们的结论,需要研究下面的极小化问题。令
。为了证明我们的结论,需要研究下面的极小化问题。令
 ,此处
,此处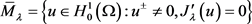 。
。
显然, 中包含系统(1.1)的所有变号解。因此,
中包含系统(1.1)的所有变号解。因此,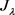 在
在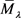 中的极小元就是系统(1.1)的基态变号解。
中的极小元就是系统(1.1)的基态变号解。
由于 ,所以
,所以 。因此,存在极小化序列
。因此,存在极小化序列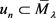 满足
满足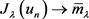 ,
,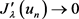 。通过与引理2.2类似的讨论,易得
。通过与引理2.2类似的讨论,易得 在
在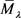 中是强制的和下方有界的。由强制性可得
中是强制的和下方有界的。由强制性可得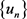 在
在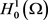 中是有界的。因此,存在常数
中是有界的。因此,存在常数 使得对于任意的
使得对于任意的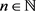 有
有 成立。应用于引理2.5类似的讨论,可得
成立。应用于引理2.5类似的讨论,可得
到对于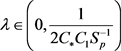 ,
,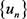 有收敛子列,此处收敛的子序列仍然用
有收敛子列,此处收敛的子序列仍然用 来表示。因此,我们不妨假
来表示。因此,我们不妨假
设在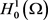 中,存在
中,存在 使得
使得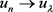 ,从而得到
,从而得到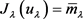 ,
,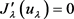 。根据
。根据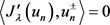 ,则
,则
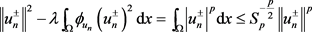 。
。
由于 ,可得到
,可得到
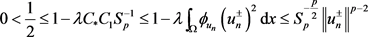 ,
,
即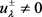 。因此,我们得到
。因此,我们得到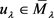 且
且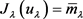 ,即
,即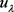 是系统(1.1)的基态变号解。综上,取
是系统(1.1)的基态变号解。综上,取
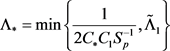 ,当
,当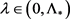 时系统(1.1)存在基态变号解。
时系统(1.1)存在基态变号解。
第二步:系统(1.1)存在基态解。考虑下面的极小化问题
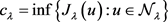 ,此处
,此处 。
。
对于任意的 ,容易得到存在唯一的
,容易得到存在唯一的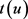 使得
使得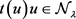 。另外,很容易得到
。另外,很容易得到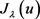 在
在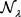 是强制下方有界的且对于任意的
是强制下方有界的且对于任意的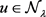 有
有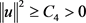 。
。
与第一步的讨论类似,我们可证明存在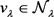 使得
使得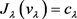 ,
,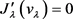 ,即
,即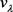 是系统(1.1)的基态解。
是系统(1.1)的基态解。
第三步: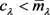 。根据第一步,可得到系统(1.1)存在基态变号解
。根据第一步,可得到系统(1.1)存在基态变号解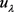 。而且存在唯一的
。而且存在唯一的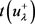 使得
使得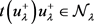 。从而根据推论2.1可得到
。从而根据推论2.1可得到
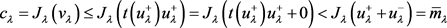 。
。