1. 引言
随着人们燃料消耗和碳排放的日益关注,锂电池由于其能量密度高、自放率低和寿命长逐渐成为最具有发展前景的化学储能电源,被广泛应用于电力输配、可再生能源并网、辅助服务、分布式微网以及电动汽车充换电等储能领域的各个方面 [1]。锂电池作为一类典型的涉及复杂电化学反应的能量存储装置,本身存在较高的安全隐患,此外,在实际运行过程中,受到当前技术水平限制,在某些情况下会发生机、电、热滥用从而引发安全问题,因此锂电池的安全性和可靠性问题十分迫切。热故障是锂电池最重要的故障之一,具有潜在的灾难性。为了更好地检测电池热动态行为以及分析电池热故障行为,对锂电池热动态行为建模是十分必要的。
现有的锂电池热模型按照维度可以划分为集总参数模型,一维、二维和三维模型 [2]。集总参数模型是将锂电池看作一个整体,同时假定锂电池内部温度均匀分布,以此获取电池的温度。一维模型是对电池在某一维度上温度分布的研究,即只计算电池在某个方向的温度分布。二维模型是对电池在某一截面上温度分布的研究。三维模型是对整个电池温度分布的研究,与一、二维模型相比,通过三维模型描述电池温度最为准确,尤其是三维模型可以直接体现锂电池的电热耦合效应,且模型易于分析处理,在扰动信号sigma等于0.1附近建模精度可达95%以上。尽管这些模型可以实现对电池模型的实时估计,但是这些模型没有考虑到电池内部电学行为与热学行为之间的耦合关系,导致电池动态热行为检测失准。
本文主要针对现有的电池热模型中存在的不足,根据锂电池充放电过程中的电化学机理,构造二阶Thevenin等效电路模型,根据产热机理,构造锂电池热模型,以电池核心温度和表面温度为状态,结合锂电池电模型,构造电热耦合模型。考虑到模型误差和测量过程中的测量噪声,设计滤波器,实现锂电池电热耦合特性建模。
2. 模型建立
锂电池在充放电时,内部的锂离子在正负极发生嵌入、脱出和转移等过程,这个过程伴随着电池内部电子得失不平衡等现象 [3]。因此,采用并联的电容和电阻元件模拟这个过程。而等效电路模型就是由电容、电阻和电压源等元器件组成。同时等效电路模型可以通过电阻元件等效电压变化,通过电压源等效电池的开路电压。目前常见的有Thevenin模型、PNGV模型、Rint模型、GNL模型。与其他模型相比,Thevenin模型结构简单,同时可以很好地反映电池的动态特性,是应用最广泛的模型。二阶Thevenin模型在一阶Thevenin模型的理论基础上多加了一个RC回路,更能准确地模拟电池的充放电行为 [4]。因此采用二阶Thevenin模型作为锂电池的电模型。图1所示为二阶Thevenin模型。
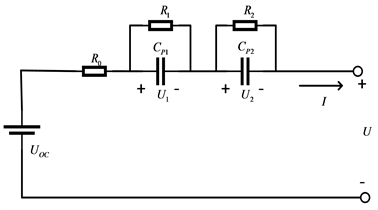
Figure 1. The schematic diagram of the second-order Thevenin model
图1. 二阶Thevenin模型示意图
该模型的数学表达式如下:
(1)
其中,
为电池两端电压,
为电池两端电压,R为电池内阻,I为电池电流。
和
分别为电化学极化电阻和电容,
和
分别为浓差化电阻和电容。
和
分别为两个RC电路的压降。
选用一个双态径向热模型 [5] 描述圆柱形锂电池的热动力学,如图2所示。
表示电池核心温度,
表示电池表面温度。双态径向模型假设锂电池表面温度相同,电池产热仅考虑两个传递过程:(1) 电池内部的热传导即电池核心到电池表面的传递,(2) 电池表面的热交换即电池表面到环境中的交换热。
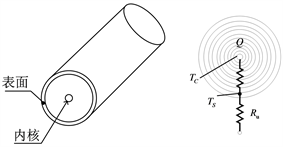
Figure 2. Two-state radial thermal model
图2. 双态径向热模型
双态径向热模型可以表示为:
(2)
式中,
表示电池核心与表面之间的等效热传导电阻。
表示电池表面与冷却空气之间的等效对流电阻。
表示环境温度。
与
分别表示电池内材料的热容系数和电池表面的热容系数。
表示电池核心的发热功率,可以表示为:
(3)
式中,I表示电池电流,U表示电池端电压,
为电池内部电压,
表示焦耳热,
表
示不可逆热。分析电池的产热机理,起主要作用的是锂电池内部产生的焦耳热,电池内部其他产热对于焦耳热可忽略不计,因此不可逆热可忽略 [6]。
电池在工作期间产生热量,影响热模型输入。将电模型与热模型结合,得到电热耦合模型,模型的状态空间方程式可以表示为:
(4)
(5)
将发热功率
和环境温度
作为输入,将表面温度
和核心温度
的测量值作为输出。经过离散化处理后,锂电池电热耦合模型为:
(6)
式中,
和
分别表示k时刻的电池核心温度和表面温度的真实值,是系统的状态向量;
和
分别表示电池核心温度和表面温度的测量值,是系统输出向量;
表示扰动噪声,
表示测量噪声。
表示状态空间矩阵;
表示输入矩阵。
3. 基于全对称多胞体滤波的电热耦合特性建模
全对称多胞体滤波是集员滤波的一种。集员滤波是假设过程噪声和观测噪声是未知但有界的滤波方法,其关键之处在于如何描述真实可行集的复杂形状。全对称多胞体滤波是用全对称多胞体近似实际可行集,通过求取能够包裹预测多胞体与参数可行集交集的最小容积多胞体来得到下一时刻状态变量的可能分布。
全对称多胞体的定义如下:
s阶全对称多胞体
是超立方体
的仿射变换 [7],即:
(7)
其中,
,
称为
的中心,
称为
的生成矩阵。
全对称多胞体有以下性质:
(8)
(9)
基于电热耦合特性建模得出的电热耦合模型,定义如下离散状态空间方程:
(10)
其中,
为系统状态向量,
为系统输入,
为系统
输出。
,
,
,
。
和
分别表示系统未知但有界的扰动噪声和测量噪声,即
,即
。
假设系统(10)的初始状态,扰动噪声和测量噪声分别满足:
(11)
其中,
分别为初始状态,扰动和噪声所在的全对称多胞体集合。
,
,
。针对电热耦合模型,设计全对称多胞体滤波器。该算法分为两步,预测步和更新步。
(1) 预测步
假设k时刻的状态向量
对应的全对称多胞体:
(12)
根据全对称多胞体的性质及系统状态方程可知,第
时刻状态向量预测集为
(13)
(14)
根据
时刻系统输出变量构造带状空间
,如下式所示
(15)
(2) 更新步
求得状态预测集
后,寻求
时刻的带状空间
与状态预测集的交集,进而得到
时刻系统状态估计范围。
为了求解
时刻系统状态估计范围,引入如下定理。
定理1 [8]. 给定全对称多胞体
、带
。若定义:
(16)
其中,
是已知矩阵,
是已知向量,
,
是指定的矩阵,则存在一个全对称多胞体能够包含
与
的交集,满足
(17)
根据引理1,则存在全对称多胞体
,满足
,并由下列各式求得
(18)
(19)
其中,
为任意矩阵,
。
不同的
对应的全对称多胞体
的形状和体积不同,为了使状态范围估计更加准确,增益矩阵
应该使得
的体积最小化,选取
的Frobenius范数作为最优性准则设计滤波器的增益矩阵
[7],表达式如下:
(20)
因此,
时刻的系统状态
的全对称多胞体集合可由公式(21)~(24)计算可得:
(21)
(22)
(23)
(24)
其中,
可由公式(14)计算可得。
结合全对称多胞体滤波算法,可以得到
的区间估计,计算公式如下:
(25)
式中,
分别表示
时刻状态估计的最小上界和最大下界。
4. 仿真示例
基于锂电池电热耦合模型,设置仿真模型参数如表1所示。
在仿真开始前,电池还没有电流流过,因此RC网络端电压
和
都为0。电热耦合模型的输入
由等效电路模型计算得到。环境温度
设为25℃,核心温度
和表面温度
的初始值都设为25℃。扰动和测量噪声限制为
。仿真结果如图3和图4所示。图3是电池核心温度的上下界估计,图4是电池表面温度的上下界估计。黑线代表温度真实值的变化情况,红线代表全对称多胞体滤波算法的上下界。从图3和图4可以看出,全对称多胞体滤波算法可以很好地跟踪状态真值,同时算法的上下界都能包裹系统状态的真实值。由此可见,全对称多胞体滤波算法能够有效地实时估计核心温度和表面温度。

Table 1. Main parameters of electro-thermal coupled characteristics of Li-ion battery
表1. 锂电池电热耦合模型主要参数
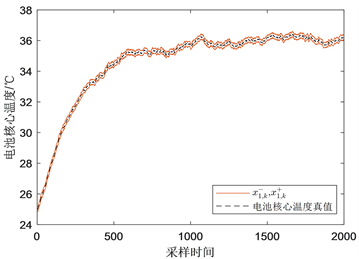
Figure 3. Upper and lower bound estimates of core temperature in battery
图3. 电池核心温度的上下界估计
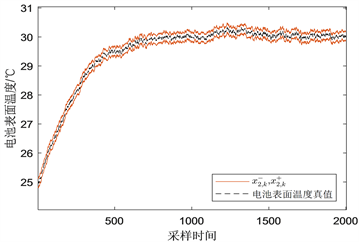
Figure 4. Upper and lower bound estimates of surface temperature in battery
图4. 电池表面温度的上下界估计
5. 结论
本文针对锂电池电热耦合动态行为和实际系统中存在的不确定但有界的噪声,结合电池产热原理与基于机理的电池等效电路模型,设计全对称多胞体滤波器,实现锂电池电热耦合特性建模,文章所提方法可以准确的提供电池核心温度和表面温度的上下界区间,且能实现对电池温度状态的紧致包裹。
基于全对称多胞体滤波的锂电池电热耦合特性建模相比于一般的电池建模,既考虑了锂电池内部电学行为与热学行为之间的耦合,又考虑了实际电池系统中的不确定但有界的噪声,有效、准确地监测电池的热学参数,具有良好的实用性,可以推广至不确定但有界的噪声下系统的状态估计。
NOTES
*通讯作者。