1. 引言
自上个世纪以来,人类社会的发展总是以难以逆转的环境变化为代价。能源消费加剧,生态环境恶化,特别是温室气体的排放使全球气候变暖,人类社会的可持续发展受到严重威胁。发展和充分利用清洁、高效的可再生能源,是推进生态文明建设、实现可持续发展的必然选择。结合能源工业发展现状,利用可再生能源发电越来越受到国际社会的广泛关注。分布式可再生能源发电靠近用户侧,能够直接供能并且便于实现多种能源形式的互补,灵活、环保和经济是其显著优势。另一方面,由于可再生能源发电的间歇性和波动性,在其接入公共电网时不免会对电网的稳定性造成一定的冲击,这对保证电能质量和提高电网的可靠性提出新的挑战,同时对公共电网的控制提出新的问题,这些因素都限制了分布式可再生能源发电的发展 [1]。
为了克服这些问题并充分利用分布式发电的优势,微网的概念应运而生 [2]。微网是由分布式电源、储能系统、负荷、监控和保护装置组成的小型发输配电系统,是能够实现自我控制和管理的自治系统。在各种可再生能源中,以分布式能源形式存在的光伏(Photovoltaic, PV)和风力发电(Wind Turbines, WT)得到了广泛关注。同时为了保证系统在间歇状态下的供电,将储能装置和柴油发电机等加入微网,提高系统运行灵活性,降低系统操作成本并确保微网的整体可靠性。
在设计微网控制系统时,重点考虑对电压和频率稳定的控制、可再生能源的即插即用能力、一次控制下的电压和频率偏差补偿、负载管理和与主网的同步等。在过去近三十年的时间里,微网的研究集中在数据采集、自动化和微网控制方面,对微网的容错控制、故障诊断以及多微网互联等方面缺乏相应的研究 [3]。
分布式发电作为未来配电系统的基石,未来将完全改变配电系统的特性。微网作为小型的发输配电系统,既可以在局部实现功率平衡和能量优化,也可以在宏观上担任配电网的微源或负荷,且建设成本较少、周期较短,使现有的电网有了更大的柔性和可控性,具有巨大的社会意义和经济潜力 [4]。由于微网具有更高的灵活性,在精准建模和控制方面具有更高的要求。同时为了提高分布式电源的渗透率以及满足不断增长的负荷要求,网络规模的扩展和调度方式的更新也是一重要问题。本文对微网的基本模型分别进行讨论,由于微网使用了不可预测和不可控的可再生能源,需要根据不同的应用场合采用不同的模型结构和鲁棒控制策略,讨论基于锁相环策略的同步技术,对并网运行或孤岛运行下微网的主从控制、集中控制和分散控制进行综述,分析多微网系统的发展现状,为今后的研究建立基础。
2. 微网的建模
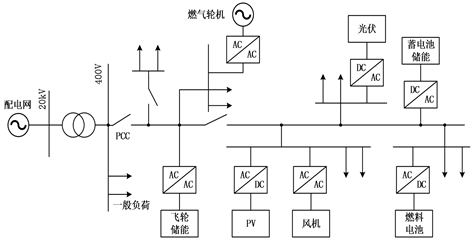
微网作为小型的电力系统,相较于传统电力系统,其具有较高的动态复杂性,应根据系统配置和类型采用不同的建模方式 [5]。精准建模是研究微网控制方式和稳定性的基础,目前尚未建立统一标准的微网模型 [6]。可再生能源的输出有三种:直流输出、变频交流输出和变压交流输出,为了维持电压稳定性,需要一个合适的体系结构来管理微源和电网之间的潮流。按照母线电能类型,将微网分为交流微网、直流微网和交直流混合微网,如图1所示。
 (a)
(a) 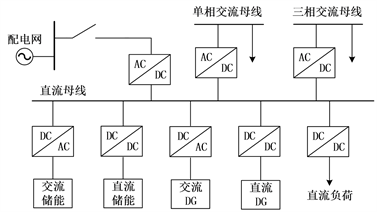 (b)
(b) 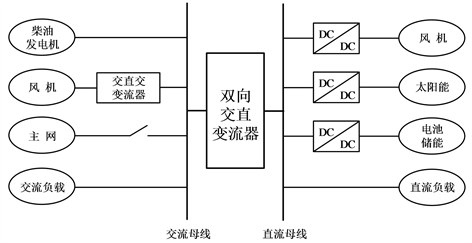 (c)
(c)
Figure 1. Microgrid structure based on photovoltaic-battery energy storage system. (a) AC microgrid structure; (b) DC microgrid structure; (c) AC/DC microgrid structure
图1. 按照母线电流划分。(a) 交流微网结构;(b) 直流微网结构;(c) 交直流混合微网结构
为了更好地与电力系统相互适应,交流微网是目前微网的主要形式,但大多数微源产生直流电,因此需要大量的电力电子转换装置,从而降低了系统运行效率,增加了系统的初始成本,并且由于转换器的开关操作,更多的谐波被引入,输出的电能质量较差是交流微网亟待解决的问题。直流微网中,由于系统输出为直流且只需要考虑电压稳定性,因此不存在谐波和频率稳定性问题 [7],降低功率损耗、降低电压降、增加线路容量是直流配电系统的优点。未来的微网呈现出交流向直流转变的形式,除此之外,直流微网无需考虑频率、相位、无功补偿等问题,控制结构简单,使其更具有广泛的应用前景。不论是交流微网或直流微网,都需要大量的电力电子器件为接口,为了解决这一问题,文献 [8] 提出了交直流混合微网结构,这种结构能够同时容纳交流负载和直流负载,但由于交直流母线之间的功率可以双向流动,同时要兼顾与电网的功率流动,因此控制方式变得更加复杂。
文献 [9] 建立了基于光伏–电池储能系统的微网模型,如图2所示。其中,逆变器控制系统的无功功率和母线电压;连接太阳能光伏阵列的DC/DC变流器控制太阳能光伏阵列的输出功率;电池储能系统通过DC/DC变流器连接到母线,变流器根据天气情况控制蓄电池组的充放电。
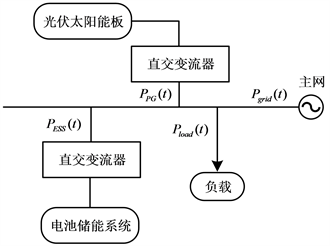
Figure 2. Microgrid structure based on photovoltaic-battery energy storage system
图2. 基于光伏–电池储能系统的微网结构
系统在并网模式和孤岛模式下的功率管理方程如下所示:
(1)
式中,
为光伏阵列的输出功率;
为电池中的功率交换;
和
分别为直流负载和交流负载消耗的功率;
为主网与微网之间的功率交换。
忽略系统的能量损耗,根据能量守恒定律和微网运行约束得到的功率方程如下式所示:
(2)
式中,
为原始负载功率;
为储能系统输出功率;
为微网供电给负荷后,需要主网向其余负载提供的功率。当
,有
;当
,有
,其中
为微网向主网输出的功率。
这种模型结构简单,变流器根据天气情况控制蓄电池组的充放电,但是对单一能源的依赖性较高,影响了微网的可靠性,容错、可伸缩性等特性需要更多的研究。为了解决单一可再生能源发电带来的电力波动和供电可靠性问题,文献 [10] 提出了集风光储于一体的混合可再生能源发电系统,如图3所示,在满足约束条件的前提下,因地制宜地最大限度利用可再生能源,并将其对电网的不利影响降至最低。由于混合微网的结构复杂性和可再生能源的波动性,这类微网在提高供电可靠性的同时对控制方式也提出了较高的要求。
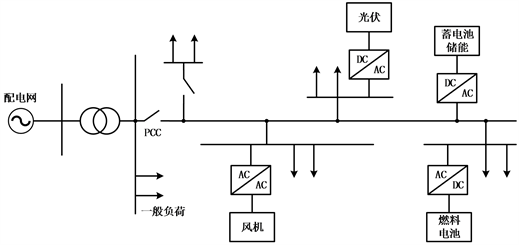
Figure 3. Microgrid structure of wind-PV-battery hybrid system
图3. 风–光–储混合微网结构
作为满足日益增长的能源需求的必然选择,分布式发电在过去几年中呈指数式增长,形成可靠的分布式系统的主要能源是风能、光伏、燃料电池和电池储能 [11]。其中,风能是发展最快、最受欢迎的电力来源。风机的输入是风力,输出是驱动发电机转子的机械动力 [12]。对于变速风机,其输出功率和转矩方程如下所示 [13] [14]:
(3)
式中,
为涡轮功率系数;
为空气密度,单位为kg/m3;A为风机叶片扫过的面积,单位为m2;Vw是风速,单位为m/s;ωm为风机的机械角速度,单位为rad/s。
根据文献 [11] [15] 可得涡轮功率系数:
(4)
风机的机械角速度和转矩的关系可由下式表示:
(5)
式中,J为转动惯量,单位为kg∙m2;Te为电磁转矩,
为机械转矩,单位为N∙m;B是转子的粘滞力,单位为N∙m∙s/rad。由上述方程,可得风机的动态模型如图4所示 [16]。
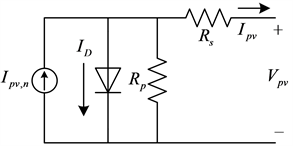
太阳能光伏系统的建模对于光伏特性的准确性十分重要,在光伏系统建模中常用的两种方法是单二极管建模和双二极管建模 [17]。其中单二极管建模较为简单 [18],双二极管建模更为复杂,但其在预测PV特性时更为准确。二者的等效电路如图5所示。
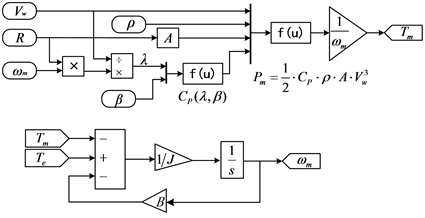
Figure 4. Dynamic model of wind turbine
图4. 风机的动态模型
 (a)
(a)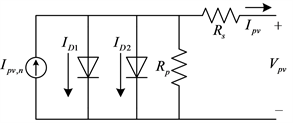 (b)
(b)
Figure 5. Single diode and double diode equivalent circuit. (a) Single diode equivalent circuit; (b) Double diode equivalent circuit
图5. 单二极管和双二极管等效电路。(a) 单二极管等效电路;(b) 双二极管等效电路
利用基尔霍夫电流定律,由单二极管等效电路可得 [11] [19]:
(6)
式中,
、
分别为光伏板的输出电流和电压;
为流过二极管的电流;
、
为串并联电阻;
、
指串并联组成一个模块的单元数;
为反向饱和电流;
为任意温度下的热电压。
双二极管的输出方程:
(7)
式中,
和
是二极管的理想常数。
为了避免电池建模的复杂性,文献 [20] 提出了通用的电池动态模型。目前,蓄电池储能系统是最有效的电化学储能技术之一,该模型采用铅酸蓄电池,当分布式电源不能产生足够的电能时,电池将提供存储的能量。电池的等效电路如图6所示,数学方程如下:
(8)
式中,Eg是储能和电池终端之间的开路电压。
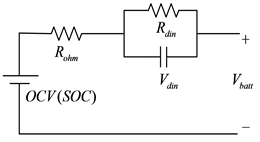
Figure 6. Battery equivalent circuit model
图6. 电池等效电路模型
3. 微网控制
尽管微网有许多优点,并且是未来智能电网的重要组成部分,但微网与配电网的接口仍存在着很多技术问题 [21] [22]。文献 [23] 讨论了变流器与电网的各种同步技巧,使并网前后逆变器电压与电网电压保持同步,最终使逆变器能够连接到电网上,即使电网电压改变了其频率、相位和振幅,微网和主网之间也能够进行功率交换。分布式电源逆变器与主网的功率分配如图7所示。

Figure 7. Power distribution between DG converter and the grid
图7. 变流器与电网之间的功率分配
分布式电源变流器与电网之间有功功率和无功功率分配如9式所示 [24]。
(9)
式中,
为电网电压;
是变流器端电压;(
)为变流器与电网之间的相角差;
是电网电源与变流器之间的线路阻抗。
当变流器与电网之间存在相角差时传递有功功率,无功功率通过调节变流器端电压和电网电压的幅值来控制 [25]。锁相环(Phase locked loop, PLL)在PCC处检测主网的电压、频率和相位 [26],是评估并网逆变器的电网参数的常用方法,具有非线性的特点,在控制微网逆变器电压输出的同时,需要调整锁相环因子以达到合适的性能,以使逆变器电压与电网电压同步。这种特性使其效率低,并且会影响控制器的性能并降低系统的稳定性。
3.1. 锁相环技术
PLL的基本框图如图8所示,相位检测用以确定相角与输入电压之间的变化,再进入环路滤波,利用环路滤波器的输出触发电压控制振荡器(Voltage Controlled Oscillator, VCO),产生电压相位角。
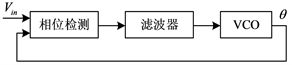
Figure 8. Basic block diagram of a phase locked loop
图8. 锁相环的基本框图
图9为并网逆变器的接线图,其中包括同步单元,实现逆变器与电网的同步。当电网电压改变其频率、相位和幅值时,逆变器可以连接到电网并向电网提供所需的电能。
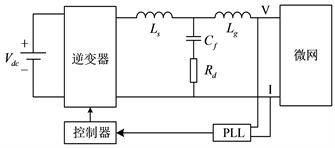
Figure 9. Grid-connected inverter structure
图9. 并网逆变器结构图
瞬时有功–无功功率理论(PQPLL)和同步参考系锁相环(Synchronous Reference Frame PLL, SRFPLL)是目前最常用的锁相环方法,这些方法通常用来分析谐波含量 [27]。当电网在初始时刻存在次谐波,此时电网震荡加剧,传统的方式并不适用,从而无法进行电压跟踪。为了克服这一问题,开发了鲁棒PQPLL技术,其原理框图如图10所示。该方法能够在存在谐波、负序不平衡和不平衡次谐波的情况下,连续跟踪电压并同步 [27]。
SRFPLL适用于三相系统,其不提供相位、频率和振幅的具体值,而只提供平均值,该方法的主要目的是检测逆变器之间公共耦合点的电压幅值和频率 [28],SRFPLL线性化小信号模型框图如图11所示。
当电网系统存在大谐波时,SRFPLL不提供相位信息,进而影响到电网信号响应。另一种方法是增强型锁相环法(Enhanced PLL, EPLL),它用于提供有关频率和序列组件的必要信息,其框图如图12所示 [29]。
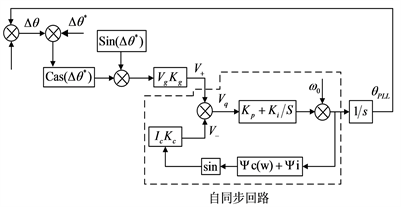
Figure 11. Linearized small signal model of SRFPLL
图11. SRFPLL的线性化小信号模型
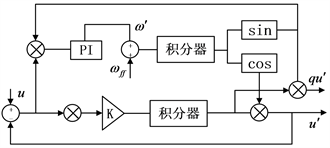
Figure 12. Linearized small signal model of SRFPLL
图12. SRFPLL的线性化小信号模型
EPLL的状态方程如下式所示 [28]:
(10)
式中,
、
、
为待选取的常数;
为输入与输出之间的变化。
正弦信号积分器锁相环(Sinusoidal Signal Integrator PLL, SSIPLL)是一种通过确定同步参考系锁相环的正序来估计主网电压的方法。该方法适用于电压畸变、电压不平衡等情况 [30],其框图如图13所示。锁相环及其改进方法是实现电网同步的常用方式,通过引入相位跟踪来提高估计精度和速度,但这种方式对谐波干扰和不确定性比较敏感,实际应用效果有待提高。对各类锁相环技术的比较如表1所示。

Table 1. Compare of PLL technology
表1. 锁相环技术的比较
3.2. 微网的协调控制策略
目前,微网的协调控制一般分为主从控制、分散控制和分层控制三种 [31],其中以中央控制器为核心的分层控制是较为主流的控制方式。集中控制策略的优势在于能够在线优化输入参数、运行设定值、约束、网络参数和信息来预测和预防故障 [32],而相对的分散式控制允许以分布式和本地的方式进行决策,拥有即插即用的潜能。在集中式控制策略中,中央控制器与本地控制器之间的通信至关重要,而分散式控制的趋势是开发位于本地控制器的第二级控制,使用本地测量数据来调节分布式单元而不是依赖于远程中央控制器的控制动作 [33]。
文献 [34] 针对孤岛模式下的直流微网,采用状态反馈的方案提出了一种新的鲁棒集中式控制器,所设计的控制器对分布式发电机组的参数不确定具有鲁棒性,并能衰减外部干扰,但设计的控制器仅针对直流微网,对用于交流微网中的性能没有进行研究且并未考虑控制器时延的影响。并网逆变器是微网的主要组成部分之一,并网逆变器的故障会对整个微网造成危害,现存文献缺乏对上述问题的研究。文献 [35] 设计了一种适用于集中控制结构的具有容错功能的双向变流器,即在逆变器故障状态下也能维持微网运行,但有待开发一种故障检测算法,以实现不同模式间的平稳切换。上述文献均未采用网络化的控制结构,而网络化控制系统具有资源共享、远程控制等优势,增加了系统的灵活性和可靠性。文献 [36] 提出了一种基于网络的混合分布式潮流控制方式,该方法由一组在每个分布式发电单元的分布式功率调节器组成,以完成对中央能源管理单元分配的最优设定值的确切跟踪。微网中央控制器对微网各部分的协调控制如图14所示 [37]。文献 [38] 提出了基于网络的主动同步方案,用于对多个分布式电源和储能系统的协调控制。在可再生能源输出波动和负荷快速变化的情况下,实现了可靠的确定性同步。传统的下垂控制方案通常用于实现电压和频率的自主调节,只考虑了局部信息而忽略了全局性能是否达到最优,针对这种问题,文献 [3] 设计了中央控制器来保持微网在不同模式下的稳定运行:在孤岛模式下,应用二次调节控制回路消除电压偏差,并实施有源补偿消除环流。在并网模式下,采用外部控制回路调节逆变器的输出功率。
文献 [39] 提出了一种适用于孤岛模式下的微网分散自趋优分层控制策略,所设计的系统不包含微网中央控制器和其与微源控制器之间的通信,通过局部反馈实现电力系统的三层控制,具有参与系统调频和优化发电机出力的能力。文献 [40] 在分散控制和集中控制的基础上,面向直流微网提出了一种新型控制架构,其中包括变流器控制层、母线控制层和调度管理层,如图15所示,分别实现了系统的可靠性和灵活性,保证了系统的能量流动和信息交互。
为了进一步提高可再生能源的渗透率以及保证日益增长的供电需求,多微网互联是有力的解决方式。现存文献对多微网系统研究停留在潮流优化和电压控制上,缺乏考虑储能系统的微网间的动态调度及性能优化 [41]。文献 [42] 对互联微网运行管理的分层随机能源管理系统进行建模,如图16所示,提出的分层能源管理策略:中央控制器负责微网的运行,计算微网内部、微网与主网之间交换的功率参考值,并
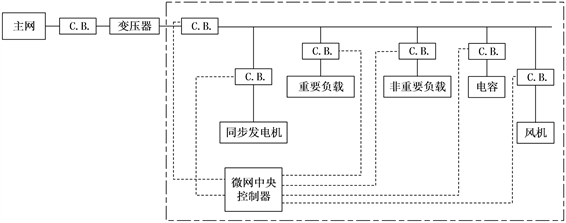
Figure 14. Block diagram of a microgrid model with microgrid central controller
图14. 微网中央控制器示意图
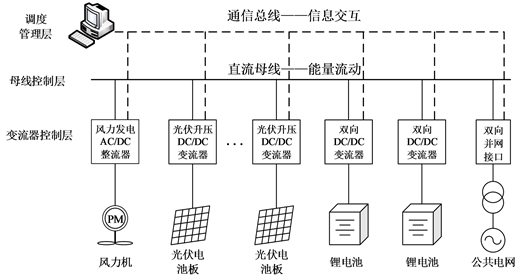
Figure 15. A new control architecture of DC microgrid
图15. 直流微网的新型控制架构
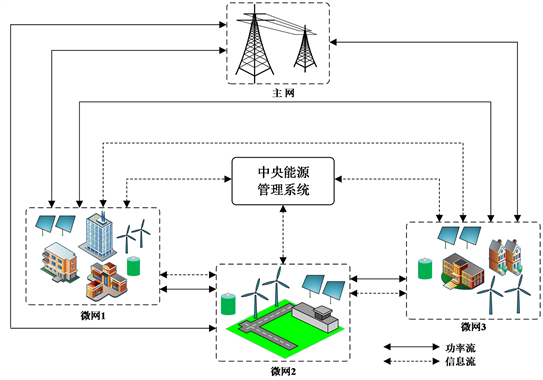
Figure 16. Control architecture of multi-microgrid system
图16. 多微网系统的控制架构
与本地的能源管理系统进行通信;在底层,考虑相邻子系统之间功率交换不确定性的影响,采用基于机会约束模型预测控制的决策方法对微网进行局部运行管理。该决策降低了微网对主网的依赖程度,最大限度地利用了网络的可用容量,但没有考虑通信故障和电力线故障等其他不确定因素。
以上文献缺乏对主从控制方式下的微网研究,主从模式的微网在海岛等偏远地区更具普适性,文献 [43] 设计了主从模式下的终端滑模控制策略,在孤岛模式下,电压和频率由采用了终端滑模控制的主分布式单元控制,从分布式单元采用传统的滑模控制,并且从分布式单元的数量可以增加,根据其各自的容量,通过功率均衡模块来分别分配参考值。文献 [44] 对主从控制模式下的独立性微网的稳定性问题进行了研究,采用特征值理论分析方法,提出了由于主电源电压环比例增益和从电源的数量和负载等变化引起的不稳定问题的解决办法,仿真验证了该方法能够有效改善系统稳定性并保证系统稳定运行。
4. 结论与展望
本文对交流微网、直流微网和交直流混合微网的结构分别进行了讨论,由于微网使用了不可预测的可再生能源,应根据不同的应用场合采用不同的模型结构和鲁棒控制策略,讨论了锁相环策略和同步技术,重点研究了对并网运行或孤岛运行下微网的主从控制、集中控制和分散控制,总结出应不同应用场合下独特的结构。
未来的微网发展应着重考虑可再生能源的波动性和间歇性以及电、热、冷协调运行等方面,合理地进行能源规划,充分利用风、光等便于获取的可再生能源,在保证微网安全、可靠运行的同时,获得最佳的经济效益。另外,微网的运行控制与保护、保证系统在不同运行模式以及在运行模式切换期间的电压和频率稳定也是微网控制的关键问题。由于微网内的电源采用电力电子技术,不免产生谐波污染,电能质量的监测与治理也是未来智能微网研究的重要课题。在微网管理中,未来应更多地考虑电能质量指标、设备寿命等,而在控制方面,负荷控制方法需要进一步研究。微网之间的互联、多代理、分散和集中控制过程为微网在电网中的发展带来了新的问题。现存文献都试图解决微网的不确定性,以及对不确定性进行准确的建模,使网络具有抗波动的鲁棒性,但当多种不确定变量同时存在时,需要一种综合的建模方法。
未来的微网与能源、信息技术的融合包含信息与计算嵌入微网能源、微网能源融入广域信息网络、基于信息的微网智能化等。同时,通过借助物联网、云计算、数据挖掘等新兴技术,为灵活地整合、管理、调度分布式资源奠定基础,提倡电网与用户的互动,将大大提高系统运行能力和接纳可再生能源的能力,进一步解决大规模分布式可再生能源的接入和消纳问题。