1. 引言
对于介质能使电容增大的现象,一个多世纪以来都是介质极化解释的。由此有介质介电和介电常数等概念,介电常数随频率变化而变化 [1]。2019年1月,有人根据地球物理勘探激电法的一次二次电压现象证明了岩石具有电容 [2],2020年1月,根据介质的充放电、介电常数等实验数据证明了介质同样是电容,介质电容不随频率变化而变化 [3]。极化说和电容说的主要矛盾在于对介质使平板电容增加的成因、弛豫时间、吸收电流、介电常数、电耗的解释完全不同。电介质理论不仅涉及化学物理基础理论,同样影响到其他相关应用学科,因此有必要分析对比上述两种矛盾的理论。
2. 介质电容理论
介质电容理论认为介质本身就是并联的若干含内阻的电容 [3]。
(1)
式中j为单位向量,ω为频率,C1、C2、Cn为介质内的并联电容,R1、R2、Rn为介质内相应电容的内阻(电容的串联电阻,电容内电导的倒数),R0为介质的(漏电)电阻(介质电导的倒数)。平行板加入介质后电容的导纳Y可写为平行板电容容纳与介质电容导纳的和,有
(2)
Cp为平行板电容为介质影响电场后的电容,其值为含介质电容频率趋于无穷的电容值。这可以理解为频率趋于无穷时,介质含内电阻电容的等效电容趋于0,电路的电容就是平行板电容Cp。式2可以写为
(3)
复电容Ci为
(4)
一定电压U下,并联的串联电容电阻的充放电I和时间t的关系可写为下式(正负符号分别电和放电),其短接充放电流I为
(5)
3. Debye介质介电常数理论
Debye给出了介电常数和弛豫时间及频率关系的公式 [4],根据该公式可以得到介电常数和损耗(电耗)的关系为一个半圆。Cole-Cole在该公式的基础上,给出一个圆弧的经验公式 [5] [6],Davidson和Havriliak又提出了斜歪的圆弧的经验公式 [7]。现代对非均匀体的研究表明,介电常数和损耗的关系可以为多个圆弧。上述关系都有相应实验数据的支持 [8] [9]。Schweidler认为Debye公式偏离实验结果是因为介质极化并非是单一的,给出了复介电常数ε公式(Ai为权重因子)和弛豫函数
经验公式公式 [10]。
(6)
(7)
4. 介质电容理论与Debye介电常数理论对比
4.1. 公式对比
Debye的介电常数半圆公式是建立在假设的基础上的 [10]。即假设在t时刻介质极化强度Pr的增长速度dPr/dt正比于其终值
与该时刻Pr之差(1/τ为比例常数)。即
(8)
而介质电容公式的推导没有假设条件。当介质的电阻很大时式4可以写为
(9)
该公式(式9)和Schweidler的公式(式6)在数学上完全一致,当n = 1时,就是Debye的半圆公式。介质充放电公式(式5)和Schweidler的弛豫函数公式(式7)在数学上完全一致,当n = 1时,就是Debye的弛豫函数公式。介质电容的两个公式和Debye的公式的一致是因为Debye推导这两个公式的假定条件(式8)和介质充放电的电压电流关系的微分方程 [2] 在数学上完全一致。该微分方程为
(10)
式中Vc为电压,I为电流,C为电容,R0为介质电阻,R1为电容内电阻。
换句话说,在数学上,Debye弛豫函数推导的假设就是把极化假设为电容。
利用介质电容公式,给定特定值(表1),可以得到Cole的圆弧,Davidson和Havriliak的斜歪圆弧以及多峰圆弧 [3] (图1、图2、图3、图4)。实际上Cole的圆弧、Davidson和Havriliak的斜歪圆弧的经验公式都可以用介质电容公式(式4)在数学上逼近(证明从略),换句话说Cole、Davidson和Havriliak的经验公式都是Schweidler的公式或介质电容公式的特例。

Table 1. Given value of capacitor and resistor of dielectrics
表1. 介质电容电阻取值表(Cp = 0.000005F)

Figure 1. Semicircle curve of equivalent Ce and periodic electrical loss Cϵ
图1. 半圆等效电容Ce和周期电耗Cϵ
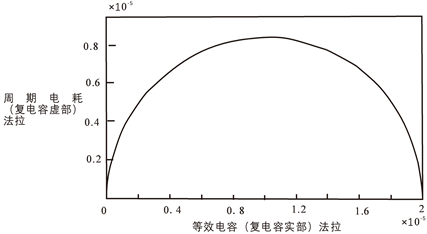
Figure 2. Arc curve of equivalent Ce and periodic electrical loss Cϵ
图2. 弧状等效电容Ce和周期电耗Cϵ

Figure 3. Slope curve of equivalent Ce and periodic electrical loss Cϵ
图3. 斜歪等效电容Ce和周期电耗Cϵ
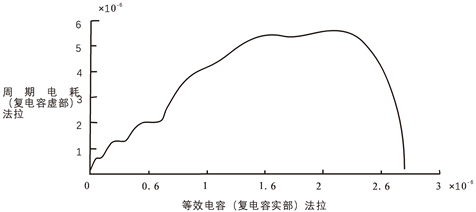
Figure 4. Multimodal curve of equivalent Ce and periodic electrical loss Cϵ
图4. 多峰等效电容Ce和周期电耗Cϵ
对于介质短接放电,可对介质电容充放电公式(式5)拟合 [3]。相对Debye弛豫函数,有很多经验公式描述非Debye体,其中Kohlrausch-Williams-Katts (KWW)函数 [4] (β伸展参数)被广泛应用
(11)
实际上,这个公式也可以用介质充放电公式(式5)和Schweidler弛豫函数(式7)通过Muntz法逼近的(证明从略)。或说数学上讲,KWW函数相当于介质充放电公式(式5)和Schweidler弛豫函数(式7)。
4.2. 放电电流方向
根据介质极化理论,在介质外加电场下,介质会产生极化电场,该电场和外加电场方向是相反的。外电场撤销后,极化电场的放电方向应该是由负极流向正极。这和实际情况相反。介质电容理论是介质电容和平行板电容的并联,因此其放电方向时从正极到负极,和实际情况相符。
4.3. 介质电容测定
交流情况下对介质电容的测定通用的为西林电桥(Resonance)法。当测试系统为可变电容(C)并联可变电阻(W)的情况下,认为介质电容就是C,电耗为1/ωWC0 (C0为不含介质时的电容)。当测试系统为可变电容(C)串联可变电阻(R)的情况下,并不认为介质电容就是可变电容(C),其电容和C0的比值
(介电常数)及电耗
如下式 [1]
(12)
(13)
结合式12和式13可以得到复式电容Ci
(14)
式14可等效于一个电容和电阻的并联,其电容Ci电导Di分别为(电阻Ri电导Di = 1/Ri)
(15)
(16)
由此可见,不管电桥系统采用电容电阻并联还是串联,都是假定介质电容和电阻都是并联来计算介质电容电耗的。
如果电桥系统按照介质电容理论设计系统电路,即用电容Cp并联若干串联电阻Ri的电容Ci及电阻R0 (电阻很大时,看作开路)。对满足Schweidler公式(式6)的介质进行电容测试时,取
(17)
(18)
(19)
可以预见,在改变系统频率时不用调整(或微调)系统电容电阻值,电桥能够保持平衡。这样的实验能够证实介质的电容并不是随频率的改变而改变的。
4.4. 无极板条件
介质极化介电常数理论都是在有极板的情况下讨论的,而介质电容不一定需要极板。对于地球物理勘探激电法中的一次二次电压现象(是在没有极板的情况下) [2],介质电容理论能够很好地解释。
4.5. 讨论
比较热运动的无序状态和电场作用下偶极矩定向排列(有序),可以看到热运动对电荷的作用是有方向的,如果说极化的作用方向是有序,热运动作用方向指向无序。或说,偶极矩是矢量,它从有序指向无序。如果说介质在电场作用(极化过程中)由于克服热运动而产生弛豫时间,那么外电场消失后,热运动则是恢复无序状态的动力,这个过程中不应该产生弛豫时间。这和事实不符合。而介质电容则认为时间常数取决于RC值,没有方向性。极化过程中,如果把定向排列看作是势能的积累,那么外电场消失后,趋于无序状态则是势能的释放,不应该产生电损。这同样与事实不符。
5. 结论
介质使电容增加的现象是因为介质本身就是电容,极化不是电容增加的原因。介质的弛豫时间就是介质电容充放电的时间常数,吸收电流就是介质电容的充电电流,电耗就是介质单位周期的电耗与平行板真空条件下电容的比值,交流状况下的介电常数反映的就是介质电容的等效电容。极化说在利用电桥测量介质电容实际假定了介质是电容和电阻的并联电路。极化说不能解释介质电容说能够解释的没有平行板条件下的一次二次电压现象。利用改进的西林电桥能够证实介质的电容不随频率改变而改变。偶极矩是矢量,它从有序指向无序。极化说的经验公式之所以能满足实验数据,是在推导经验公式时,在数学上实际把极化强度变化假设为电容的电压变化。