1. 前言
MRD作为智能控制的执行器或被控对象应用于车辆半主动悬架系统,具有可控性强、频率响应高、阻尼力可调范围广、低成本低能耗等特点 [1],在动态特性上更能满足减振防护的要求,因此MR悬架系统具有良好的发展前景。
由于MRD本身固有的高度非线性和滞环特性,MR悬架系统在路面不平度激励下可能导致车辆产生诸如分岔、混沌等复杂的非线性振动 [2],这种非线性动力学现象不利于大多机械振动系统。一是混沌振动时极大程度上会增大系统噪声,加剧悬架振动,二是造成机械系统内部零件磨损,甚至存在轮跳和翻车的危险,严重影响行车安全。因此国内外学者对MR悬架非线性动力学行为进行了大量研究。
准确模拟MRD非线性特性和耗能特性是保证半主动精准控制的前提和出。目前应用较为广泛的是参数化模型有Bingham模型 [3]、非线性双粘性模型 [4]、Sigmoid模型 [5]、Bouc-Wen模型及其修正Bouc-Wen模型 [6]。李等 [7] 考虑电流控制和激励性质对MRD输出阻尼力的影响,提出了双Sigmoid模型。徐等 [8] 充分考虑温升效应对MRD力学性能的影响,提出了包括质量元素的温度唯象模型,仿真结果表明该模型不仅能呈现MRD的静摩擦黏滞效应和力衰减现象,同时模拟出其内部阻尼力–位移(F-x)阻尼力–速度(F-v)非线性关系。臧等 [9] 引入行为指数n并且结合遗传算法获得最优模型参数,得到了改进的S型滞环模型,仿真表明该模型能准确地描述高速度区的饱和特性。陶 [10] 讨论了MRD参数化模型的优缺点,指出利用神经网络等智能算法拟合的非参数化模型不仅可以描述MRD工作特性,还能准确地反映MRD的逆向动态特性。
在车辆悬架模型的非线性动力学研究领域,黄等 [11] 采用Sigmiod模型建立二自由度悬架模型,研究了系统在谐波激励频率、幅值变化下的分岔特性,结果表明系统运动状态对路面激励变化非常敏感。张等 [12] 基于修正Bouc-Wen模型系统地分析了单频激励下二自由度悬架系统的非线性动力学特性,并进一步设计了线性反馈控制器抑制系统混沌振动。吴 [13] 通过相平面图、分岔图和庞加莱截面图揭示了路面变化或MR悬架系统自身参数变导致系统发生混沌振动。
目前对非线性悬架系统的建模及动力学响应问题已有研究,然而有关MRD输出阻尼力计算模型的成果多局限于拟合阻尼器的实验数据,追求得到精确的非线性滞环模型,尚缺乏研究MRD滞环模型对悬架的非线性动力学特性的影响。
揭示非线性动力系统的分岔、复杂混沌运动一直是提升悬架动力学性能的热点。本文以二自由度MR悬架为研究对象,针对国际上已提出的三种典型模型:Sigmoid模型、修正Bouc-Wen模型、S型模型,结合天棚(Skyhook)半主动控制原理,采用数值方法研究三种滞环模型的MR悬架在路面激励频率、幅值变化下通向混沌振动的路径,分析比较不同MRD滞环模型悬架系统的振动响应。
2. MRD滞环模型
本文采用的MRD滞环模型考虑了电流控制,将电流控制对MRD输出阻尼力的滞环特性从模型中分离出来 [14],通过改变MRD的外加电流控制外加磁场,进而改变MRF中磁性颗粒的黏滞特征,实现MRD输出阻尼力Fd连续可调。得到电流控制MRD的通用滞环模型表现为
(1)
式中,Fd表示MRD的输出阻尼力,i表示MRD的控制电流,x表示MRD活塞的相对位移,
表示MRD活塞运动的相对位移速度,
表示MRD活塞运动的相对位移加速度,
表示MRD的电流控制函数,
表示MRD非线性滞环算子。
电流控制函数
,如下式
(2)
2.1. Sigmoid模型
基于对称和不对称的Sigmoid函数,王等 [15] 构建了一种通用MRD滞环模型,其结构简图如图1所示,对称的Sigmoid函数反映MRD在特定激励和控制电流下的典型F-v特性较为接近,其滞环算子为
(3)
(4)
(5)
(6)
(7)
式中Fh(v)为滞环算子函数;vh表示阻尼力过零点时的速度;σ表示滞环的斜率;kv表示激励性质变化时对阻尼力的影响系数;vm表示激励信号的峰值速度。
2.2. 修正Bouc-Wen模型
为了能拟合实验结果,Wen [16] 对Bouc提出的迟滞模型加以发展和完善,提出了Bouc-Wen模型。Spencer等 [17] 提出了基于Bouc-Wen模型的现象模型,简称现象模型,该模型结构如图2所示,由Bouc-Wen单元、粘滞阻尼单元和弹簧元件组成。
计算滞环式子的表达式
(8)
(9)
(10)
式中,k0表示弹簧元件的刚度系数;k1表示MRD蓄能器刚度系数;c0表示高速情况下粘滞阻尼系数;c1表示低速情况下粘滞阻尼系数;x0表示弹簧k1的初始位移;y,x为内变量;通过调整参数β、γ、n和A可以改变F-v曲线的形状。
2.3. S型滞环模型
杨 [18] 采用神经网络理论中神经元S型传递函数,并结合改进的非线性Binghan模型,即将非线性Binghan模型中的符号函数用双曲正切S型传递函数tansgn代替,提出了S型滞环模型,其计算滞环式子为:
(11)
(12)
(13)
(14)
式中,cp表示磁流变材料屈服后塑性粘度系数;k表示气体蓄能腔所形成的刚度系数;tansgn表示神经网络模型的神经S型传递函数。
3. 基于MRD的车辆悬架模型
3.1. 二自由度MR悬架系统模型
车辆悬架是由弹簧、阻尼器、轮胎等非线性器件组成的复杂系统 [19],当仅考虑汽车悬架系统的平顺性,即车辆垂直方向的振动特性时,可以根据研究对象的不同进行简化,本文为了探究MRD滞环模型对车辆悬架非线性影响采用二自由度车辆悬架模型。该模型中参数少、结构简单,但是能基本反映车辆悬架行驶过程中车身垂直方向的振动加速度、悬架动行程以及轮胎动载荷这些本质特征。

Figure 3. 2-DoF MR suspension system dynamics model
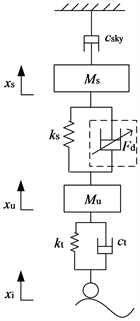
图3. 二自由度MR悬架系统动力学模型
图3示出了二自由度MR悬架系统模型。其中ms、mu分别为簧载质量和非簧载质量;ks、kt分别为悬架弹簧刚度和车轮等效刚度;ct为车轮阻尼系数,xs、xu分别为簧载质量位移和非簧载质量位移;xin为路面激励位移;Fd为MRD输出的可控阻尼力。根据牛顿运动定律,该悬架系统的动力学方程为:
(15)
(16)
3.2. 基于改进Skyhook的半主动控制策略
半主动悬架中控制策略的好坏直接影响到控制效果的优劣,结合实际应用的要求,本文采用基于改进天棚半主动控制策略。
“天棚”(Skyhook)阻尼控制策略是由Karnopp [20] 提出的一种经典车辆悬架阻尼控制方法,目前在车辆半主动悬架系统振动控制中被广泛采用。理想模型如图4(a)所示,假设将系统中的阻尼器位于簧载质量与某固定的“天棚”之间,使其作用力方向与簧载质量相反,从而抑制车身振动。理想的阻尼力为:
(17)
其中,csky是天棚阻尼系数,根据悬架系统参数优化确定。
 (a)
(a)  (b)
(b)
Figure 4. Skyhook control. (a) Ideal skyhook damping system model; (b) Improved skyhook damping system model
图4. 天棚阻尼控制。(a) 理想天棚阻尼系统模型;(b) 改进型天棚阻尼系统模型
如图4(a)所示的天棚阻尼是一种理想模型,没有考虑到在
时的控制状态以及各状态变量测量等问题,所以单纯的天棚很难实现,可以采用等效性在一定的范围内实现天棚阻尼控制如图4(b)所示,在簧载质量与非簧载质量之间的半主动控制阻尼器的阻尼力可以根据控制策略的变化而变化。为实现天棚阻尼控制,结合MR阻尼器的工作特点基于改进型天棚阻尼控制器的系统框图如图5所示,改进型天棚阻尼控制方案以驱动电流的形式给出:
(18)
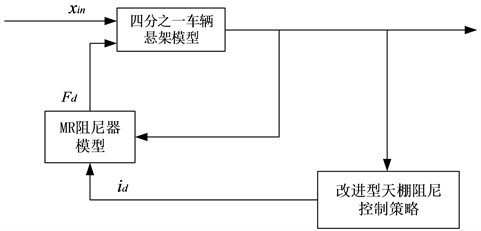
Figure 5. System framework of improved skyhook damping controller
图5. 改进型天棚阻尼控制器的系统框架
4. MR悬架系统非线性动力学分析
4.1. MRD滞环模型验证

Table 1. Three hysteresis model parameters
表1. 三种滞环模型参数
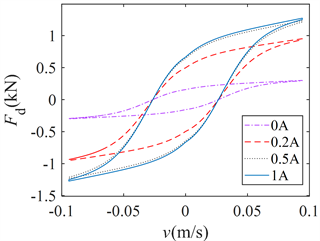
为验证MRD滞环模型对悬架性能的影响,首先对三种滞环模型F-v特性曲线计算结果进行比较分析,采用模型参数如表1所示。图6示出了不同控制电流下三种模型的滞环F-v特性曲线,正弦激励信号的幅值为0.01 m,幅值为1.5 Hz,控制电流分别为0 A、0.2 A、0.3 A、0.5 A。从图6中可以看出,在不同控制电流下,三种模型具有良好的一致性,表明非线性饱和的电流控制函数准确描述了电流对阻尼力的控制特性。
 (a)
(a) 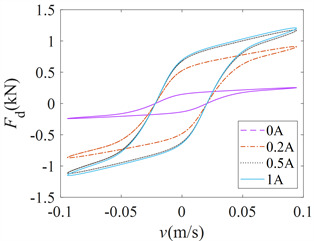 (b)
(b)  (c)
(c)
Figure 6. F-v characteristic curve at different control currents. (a) Sigmoid; (b) Modified Bouc-Wen; (c) S
图6. 控制电流不同时F-v特性曲线。(a) Sigmoid;(b) 修正Bouc-Wen;(c) S
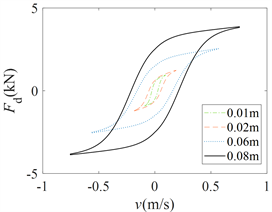
图7示出了正弦激励信号频率为1.5 Hz,控制电流为0.2 A,正弦激励信号幅值分别为0.01 m、0.02 m、0.06 m、0.08 m时滞环F-v特性曲线。图8示出了正弦激励信号幅值为0.01 m,控制电流为0.2 A,正弦激励信号幅值分别为1.5 Hz、5 Hz、15 Hz时滞环F-v特性曲线。
由图7(a)、图8(a)可以看出,当改变路面激励幅值和频率时,Sigmoid模型滞环F-v特性曲线没有改变;而从图7(b)、图8(b)可以看出,Bouc-Wen模型在低速时F-v特性曲线坡度变小,能够描述MRD在低速时的滞回性能。并且随着激励幅值和频率的增加,滞回宽度增大,最大屈服力在增加,阻尼力明显增大;对于S模型而言,从图7(c)、图8(c)可以看出若增大激励幅值和频率,在低速时F-v特性曲线坡度变小,非线性变大。
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 7. F-v characteristic curve with different excitation amplitudes. (a) Sigmoid; (b) Modified Bouc-Wen; (c) S
图7. 激励幅值不同时F-v特性曲线。(a) Sigmoid;(b) Bouc-Wen;(c) S
 (a)
(a)  (b)
(b) 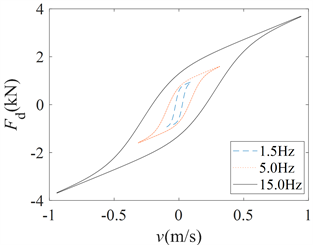 (c)
(c)
Figure 8. F-v characteristic curve with different excitation frequency. (a) Sigmoid; (b) Modified Bouc-Wen; (c) S
图8. 激励频率不同时F-v特性曲线。(a) Sigmoid;(b) 修正Bouc-Wen;(c) S
上述仿真结果表明,Sigmoid模型、修正Bouc-Wen模型、S型模型均可以描述MRD非线性饱和的电流控制特性,且F-v特性曲线对激励幅值、频率变化较为敏感,但控制电流对其影响较小。同时也可以反映出Sigmoid模型在激励性质变化时适应能力优于修正Bouc-Wen模型和S型模型。
4.2. MR悬架系统非线性动力学仿真结果
在分析路面随机激励下系统发生分岔、混沌等非线性动力学行为时,很少涉及MRD滞环模型对系统振动响应的影响。因此研究MRD滞环模型对MR悬架系统非线性振动的影响,有利于MRD结构改进与滞环模型设计,避免混沌运动造成车辆失稳影响悬架整体性能,对半主动悬架控制具有重要的理论意义与工程价值。
选择谐波路面作为路面输入,即
,其中f表示激励频率,amp表示激励幅值。系统参数簧载质量ms = 288.9 kg,非簧载质量mu = 28.58 kg,悬架刚度系数ks = 19,960 N/m,轮胎刚度系统kt = 155,900 N/m,轮胎等效阻尼系统ct = 100 N/(m∙s−1)。
1) 激励频率f变化时MR悬架系统的非线性特性
实际路面扰动的幅值通常为1~10 cm,幅值越大,表明当前路面不平整度越大,影响车辆行驶时平顺性和操控性。当悬架系统幅值保持不变,但车速产生变化时,路面对车辆的激励频率将随之发生变化。因此,本小节考虑两种路况下即amp = 2 cm和amp = 8 cm,对基于三种不同滞环模型的MR悬架系统簧载质量位移xs进行时域仿真。
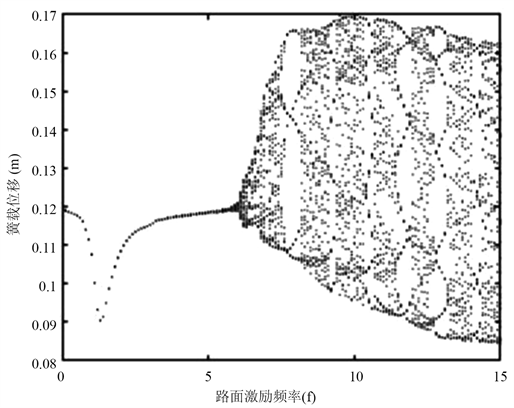
图9所示的是amp = 2 cm路况较好时的局部分岔图,由图中可以看出,Sigmoid模型悬架系统在6.5 Hz时最先进入混沌运动,随后进入周期与混沌运动交替的状态。修正Bouc-Wen模型悬架系统在6.4 Hz时由周期3运动随后短暂进入周期5,在7.2 Hz时系统出现混沌运动。S模型悬架系统在9.2 Hz时由周期1进入混沌运动。从图中可以直接观察到,系统随着激励频率的增大,MR悬架会处于周期与混沌运动交替的状态,当系统处于混沌振动时,其运动的不稳定和无规律会加剧系统内部振动,减短零部件使用寿命,威胁到行车安全。
 (a)
(a)  (b)
(b) 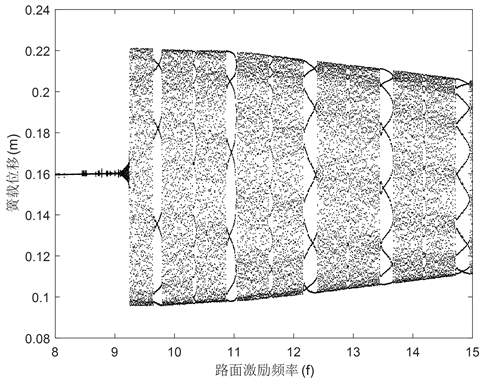 (c)
(c)
Figure 9. Bifurcation diagram of suspension system sprung mass displacement at amp=2cm. (a)Sigmoid; (b) Modified Bouc-Wen; (c) S
图9. amp = 2 cm悬架系统簧载质量位移xs分岔图。(a) Sigmoid;(b) 修正Bouc-Wen;(c) S
图10所示的是悬架模型在路况较差amp = 8 cm时的分岔图,由图10(b)可以看出修正Bouc-Wen模型悬架系统相较于图9(b)路况较好时,随着f的增加悬架系统在f = 3.3 Hz时更早进入周期与混沌运动交替的状态。由图10(a)、图10(c)可知Sigmoid模型悬架系统和S模型悬架系统分别在4.5 Hz、8.9 Hz时由周期1进入混沌运动,说明修正Bouc-Wen模型悬架系统在路面激励增大的情况下提前进入混沌运动状态,而Sigmoid模型悬架系统和S模型悬架系统响应受影响较小。
 (a)
(a)  (b)
(b) 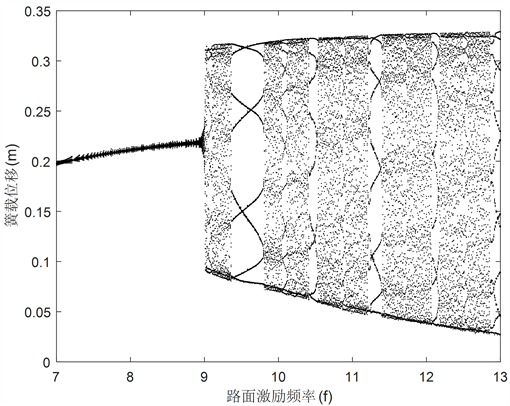 (c)
(c)
Figure 10. Bifurcation diagram of suspension system sprung mass displacement at amp = 8 cm. (a) Sigmoid; (b) Modified Bouc-Wen; (c) S
图10. Amp = 8 cm悬架系统簧载质量位移xs分岔图。(a) Sigmoid;(b) 修正Bouc-Wen;(c) S
2) 激励幅值amp变时MR悬架系统的非线性特性
车辆悬架系统存在两个固有频率,分别是低频段的簧载固有频率和高频段的非黄载固有频率。本节选取路面输入激励频率分别为3.2 Hz和11.5 Hz对三种不同计算模型的MR悬架系统动力学特性进行分析。
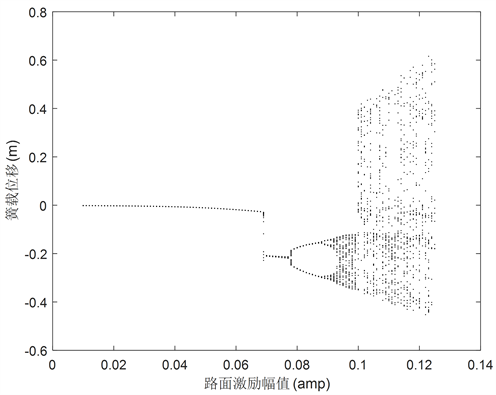
图11为f = 3.2 Hz时三种滞环模型MR悬架系统簧载质量位移xs随激励幅值变化的分岔图。从图11(a)可以看出,Sigmoid悬架系统在激励幅值变化过程中,系统主由倍周期分岔联至混沌运动。当amp小于6.8 cm时,系统处于稳定周期1;随着激励幅值的增大,系统由稳定的周期1进入周期2;当amp大于9.2 cm时,系统进入混沌运动状态。图11(b)反映修正Bouc-Wen悬架系统在[1.5 cm, 2.5 cm]区间内和大于4 cm区间内系统发生混沌振动。图11(c)直观描述了S模型悬架系统在[0.1 cm, 3.8 cm]区间内系统处于稳定周期1;在[3.8 cm, 5.0 cm]区间系统处于周期3,随后系统进入混沌运动,当激励幅值大于6.5 cm时,系统重新进入周期1。
 (a)
(a)  (b)
(b) 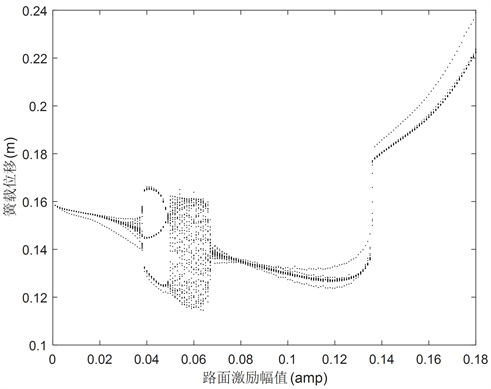 (c)
(c)
Figure 11. Bifurcation diagram of suspension system sprung mass displacement at f = 3.2 Hz. (a) Sigmoid; (b) Modified Bouc-Wen; (c) S
图11. f = 3.2 Hz悬架系统簧载质量位移xs分岔图。(a) Sigmoid;(b) 修正Bouc-Wen;(c) S
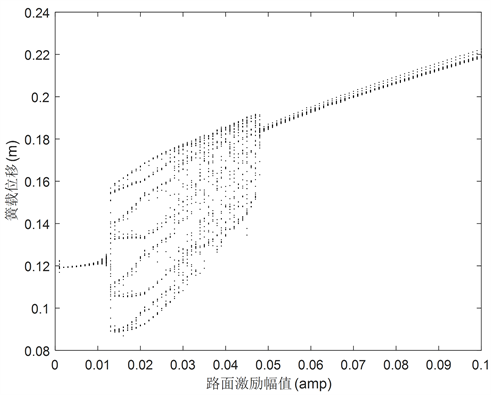
图12为f = 11.5 Hz时三种滞环模型MR悬架系统簧载质量位移xs随激励幅值变化的分岔图。从图12(a)可以看出,Sigmoid模型悬架系统在amp小于1.2 cm时,系统处于稳定周期1;随着激励幅值的增大,系统由稳定的周期1进入周期8;当在[3 cm, 4.8 cm]区间内时,系统进入混沌运动状态;当amp大于4.8 cm时,系统重新进入周期1。图11(b)描述了修正Bouc-Wen悬架系统在小幅值时就进入周期9;
 (a)
(a)  (b)
(b) 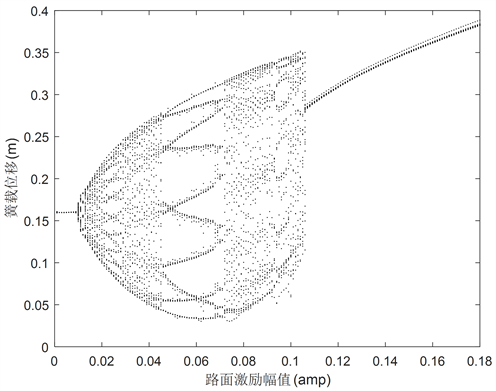 (c)
(c)
Figure 12. Bifurcation diagram of suspension system sprung mass displacement at f = 11.5 Hz. (a) Sigmoid; (b) Modified Bouc-Wen; (c) S
图12. f = 11.5 Hz时悬架系统簧载质量位移xs分岔图。(a) Sigmoid;(b) 修正Bouc-Wen;(c) S
在amp = 0.9 cm时系统发生极为短暂的混沌运动,随后系统进入周期9;当amp = 2 cm时系统发生混沌运动;在amp在区间[5.5 cm, 9.1 cm]内系统进入周期2;amp大于9.1 cm时系统发生混沌运动。从图12(c)可以看出S悬架系统在区间[0.001 cm, 0.016 cm]内系统处于稳定周期1,随后进入混沌运动;在区间[2.0 cm, 2.9 cm]内系统短暂处于周期19,随后系统进入混沌运动;当激励幅值大于4.2 cm时,系统重新进入周期10;当amp = 7.2 cm系统又进入混沌运动;当amp大于10.5 cm时,S模型悬架系统进入稳定周期1。
上述仿真结果表明,在路面激励幅值变化时,三种悬架系统均经历了周期运动、混沌运动等丰富动力学行为。在低频段时,Sigmoid模型悬架系统在小幅值激励响应下能保持稳定的周期1状态,修正Bouc-Wen模型悬架系统和S模型悬架系统均出现混沌区域,而随着幅值增大S模型悬架系统能恢复到稳定状态。在高频段时,随着幅值增大Sigmoid模型悬架系统和S模型悬架系统能摆脱混沌状态进入周期运动,而修正Bouc-Wen模型悬架系统无法脱离不稳定的非线性振动。
5. 结论
本文基于二自由度MR悬架系统的动力学模型,通过簧载质量位移xs的分岔图系统地研究了路面激励信号频率和幅值变化时,三种MRD滞环模型对悬架系统非线性振动的影响,根据观测MR悬架系统的动力学演化过程,得出以下结论。
1) 路况较好时,MR悬架系统对频率变化较为敏感。当路面激励信号频率较小时,基于三种模型的悬架系统均能长久保持周期运动;随着路面激励信号频率增大,悬架系统会多次出现混沌振动,基于Sigmoid模型的悬架系统最先进入混沌振动,但振动幅值最小。
2) 路况较差时,基于修正Bouc-Wen模型的悬架系统提前进入混沌振动,而对Sigmoid模型悬架系统和S模型悬架系统影响较小。
3) 路面激励信号频率较小时,Sigmoid模型悬架系统能长久保持周期运动,仅在amp大于0.092 m即路况极其糟糕的情况下,才会进入混沌振动;S模型悬架系统在0.05 m~0.065 m出现混沌振动,修正Bouc-Wen悬架系统则在大于0.04 m情况下长期处于混沌振动。
4) 路面激励信号频率较大时,Sigmoid模型悬架系统在0.03 m~0.048 m区间内,S模型悬架系统在0.016 m~0.020 m、0.029 m~0.042 m、0.072 m~0.0105 m区间,修正Bouc-Wen模型悬架系统在0.020 m~0.055 m区间内均出现不同程度的混沌振动。
上述研究表明:MR悬架系统属于强非线性系统,在路面激励输入下系统极易出现复杂的非线性动力学行为。MRD滞环模型的不同也会改变悬架系统非线性动力学行为,Sigmoid模型悬架系统在抑制混沌振动中优于修正Bouc-Wen模型悬架系统和S模型悬架系统,因此Sigmoid模型非常适用于MRD的工程设计和应用。本文研究结果对MR系统半主动控制策略的研究有着十分重要的指导意义,可以通过修正MRD滞回模型和完善控制器设计来有效抑制MR悬架系统混沌振动的发生。
NOTES
*通讯作者。