长江上游气温时空变化特征分析

Analysis of Spatial and Temporal Variation of Air Temperature in the Upper Reaches of the Yangtze River

摘要: 为了获得长江上游地区在全球变暖背景下的气温时空变化特征，本文利用中国气象局国家气候中心提供的长江上游近60年的逐日平均气温资料，通过趋势分析、Morlet小波变换以及M-K突变分析方法，对长江上游气温的时空变化特征进行了分析。结果表明：1) 从空间分布上看，长江上游多年平均气温自西北向东南逐渐升高；而在变化趋势上，长江上游平均气温升温趋势自西北向东南减弱，其中长江源区和金沙江水系区域升温幅度最大。2) 长江上游地区1961~2020年的多年平均气温为12.1℃，近60年平均气温上升趋势显著，增温率为0.194℃/10a，并且21世纪00年代增幅最大，同时，四季中以冬季增温最为明显。3) 长江上游地区平均气温突变发生在2001年，春、夏、秋、冬四季平均气温突变时间分别为2003、2005、1998和1997年前后。在周期变化方面，近60年来长江上游地区夏季和冬季的平均气温在3 a、6~7 a和10~15 a的时间尺度上都存在周期变化。

Abstract: In order to obtain the upper Yangtze River region in spatial and temporal variation characteristics under the background of global warming temperatures, using the daily average temperature data in the upper reaches of the Yangtze River in recent 60 years provided by the National Climate Center of China Meteorological Administration, this paper analyzes the temporal and spatial variation characteristics of temperature in the upper reaches of the Yangtze River through trend analysis, Morlet wavelet transform and M-K catastrophe analysis. The results show that: 1) In terms of spatial distribution, the annual mean temperature in the upper reaches of the Yangtze River increased gradually from northwest to southeast; on the other hand, the warming trend of average air temperature in the upper reaches of the Yangtze River weakened from northwest to southeast, with the largest warming in the source region of the Yangtze River and the Jinsha River system. 2) The annual average temperature in the upper reaches of the Yangtze River was 12.1˚C from 1961 to 2020, and the average temperature increased significantly in the last 60 years, with a warming rate of 0.194˚C/10a. The increase rate was the largest in the 2000s, and winter was the most obvious temperature increase in the four seasons. 3) The abrupt change of mean temperature in the upper reaches of the Yangtze River occurred in 2001, and the abrupt change time of spring, summer, au-tumn and winter were around 2003, 2005, 1998 and 1997, respectively. In terms of periodic variation, the average temperature in summer and winter in the upper reaches of the Yangtze River has a periodic variation on the time scales of 3 a, 6~7 a and 10~15 a in the last 60 years.

1. 引言

目前，全球变暖是近百年来气候变化的突出特征之一 [1]。联合国政府间气候变化专门委员会第五次评估报告中指出，自1950年以来，世界各地几乎所有的地区都存在某种程度的变暖，1880~2012年全球地表平均温度上升了0.85℃，而中国1905~2001年的年平均气温升高了0.79℃ [2]。在全球变暖的大背景下，许多气象灾害的发生越来越频繁。而作为世界“屋脊”和世界“第三极”的青藏高原也已成为了许多气象学家钻研气候变化波动的焦点区域，青藏高原的气候变化不只影响着我国西南地区，更是对全球的气候波动有触发的作用 [3] [4]，而从青藏高原腹地至湖北宜昌的长江上游是中国重要并且影响范围广泛的生态功能区 [5]。故此，针对长江上游平均气温的时空变化特征开展研究不仅对我国乃至对全球的气候发展变化都具有重要的意义。

关于长江上游平均气温的时空变化特征，已经有许多学者做了相关研究，并得到了一定的成果：马振峰等 [6] 在2003年就长江上游夏季气温的时空变化进行了研究，并提出夏季气温存在阶段性变化的观点。姜彤等 [7] 和王艳君等 [8] 在2005年的研究表明，近几十年长江流域的年平均温度呈上升趋势，并且上世纪90年代升温幅度最大、升温趋势最明显。在此基础上，丁斌等 [9] 指出20世纪90年代增温幅度处于0.3~0.6℃/10a之间。随后，曾小凡 [10] 等研究发现，长江上游增温幅度在0.20℃/10a左右，同时指出其主要的增温区域为金沙江流域。同年，周德刚等 [11] 发现长江上游西北部升温趋势比较显著，并且通过季节比对发现平均气温在冬季比在其他季节的增温更加明显。而在空间分布方面，钟晨晨等 [12] 和王雨茜等 [13] 的研究结果显示，长江上游平均气温呈现东部南部向西北部递减的分布规律。在周期变化上，孙甲岚等 [14] 得出了长江上游年平均气温的相位变化主要以3 a、7 a和31 a为周期。随后关颖慧等 [15] 和吴双桂等 [16] 突变检验上有了新进展，其研究发现年平均气温的突变发生在1997年，并且冬季气温突变发生在年平均气温突变之前。

以上的研究成果可以大概说明长江上游气温的时空变化特征，但是上述研究选取的时间序列较短，不够具有代表性，并且在平均气温的变化趋势空间分布方面的研究有所欠缺，不够全面和深入，因此本文在上述研究的基础上，对1961~2020年长江上游气温的时空变化特征开展研究是十分必要的。

本文以长江上游流域68个气象站点的逐日日平均气温资料为基础，结合小波分析和M-K趋势检验等方法，分析长江上游流域1961~2020年(近60年)平均气温的空间分布和时间变化特征，对合理开发利用长江流域的水资源，提高灾害管理和预防能力，并促进开展中国气候变化研究都具有重要的作用 [17]。

2. 资料与方法

2.1. 研究区域与资料概况

本文利用的是1961~2020年的中国气象局国家气候中心的逐日日平均气温资料，该资料包含全国站点数据，从中选取包含在长江上游区域内的68个站点，这些站点观测完整，缺测值少，并且在所选年份之间变动不大。在1961年之后，我国的地面气象观测站覆盖更加全面，因此本文用到的数据都具有科学性。

长江上游区域范围如图1所示，长江上游经纬度范围为90˚~112˚E，24˚~36˚N，其覆盖面积宽广，影响范围广泛，先后涉及青海、西藏、四川、云南、重庆、湖北等省、区、市。长江发源地以下至四川宜宾为金沙江江段，长约3463千米，落差大，约占全江落差的95%，四川宜宾以下至湖北宜昌为长江上游干流，长约1040千米。整个长江上游区域主要汇入了雅砻江、岷江、嘉陵江和乌江等支流。

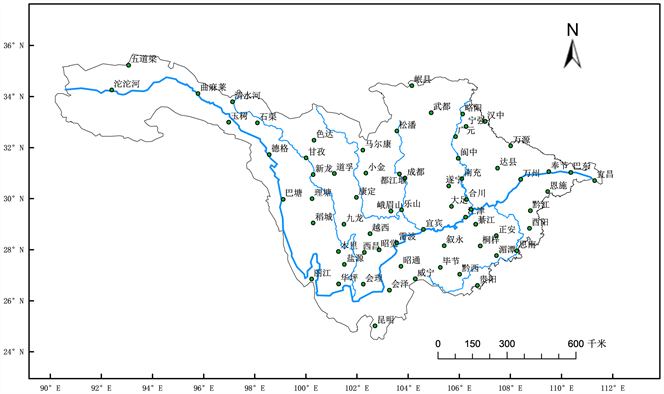
Figure 1. Distribution of meteorological stations in the upper reaches of the Yangtze River (the thick blue lines are the main stream of the Yangtze River, and the thin lines are the tributaries of the Yangtze River)

图1. 长江上游气象站点分布图(蓝色粗线条为长江干流，细线条为长江支流)

2.2. 研究方法

本文主要运用三种方法来分析气温的时空变化特征：用线性回归方法来分析气温的主要时间变化趋势；用Mann-Kendall突变检验法对其做相应的突变分析并确定突变时间；用小波分析法来研究平均气温的周期变化。

2.2.1. 线性回归

线性回归是一种统计分析方法，用于确定两个或两个以上变量之间的定量相互依存关系。本文采用一元线性回归分析方法进行趋势分析。

用 $y_i$ 表示样本量为n的某一变量，用 $x_i$ 表示 $y_i$ 对应的另外一组变量，建立起 $y_i$ 和 $x_i$ 之间的线性关系：

$y=bx+b_0$ (1)

其中：

$\{\begin{array}{l}{b}_0=\bar{y}-b\bar{x}\\ b=\frac{{\displaystyle {\sum }_{i=1}^n{x}_i{y}_i}-\frac{1}{n}\left({\displaystyle {\sum }_{i=1}^n{x}_i}\right)\left({\displaystyle {\sum }_{i=1}^n{y}_i}\right)}{{\displaystyle {\sum }_{i=1}^n{x}_i^2}-\frac{1}{n}{\left({\displaystyle {\sum }_{i=1}^n{x}_i}\right)}^2}\end{array}$ (2)

式中b为回归系数， $b_0$ 为回归常数。回归系数b的符号反映了变量y的倾向方向。B > 0表明变量y随着变量x的增加而上升，b < 0表明变量y随着变量x的增加而下降，b值的大小表示变量y随变量x变化的倾向速率。

上述趋势倾向的显著性可通过F检验来判别，构造F统计量：

$F=\frac{r^2}{\frac{1-r^2}{n-2}}$ (3)

其中r为变量x与变量y的相关系数，按下式计算：

$r=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{x}_i^2}-\frac{1}{n}{\left({\displaystyle {\sum }_{i=1}^n{x}_i}\right)}^2}{{\displaystyle {\sum }_{i=1}^n{x}_i^2}-\frac{1}{n}{\left({\displaystyle {\sum }_{i=1}^n{y}_i}\right)}^2}}\times b$ (4)

统计量F遵从分母自由度为(n − 2)、分子自由度为1的F分布，对于给定的显著性水平 $\alpha$ (0.05)，可以得到临界值 $F_{\alpha }$ (4.007)，当 $F>F_{\alpha }$ 时，回归方程被认为是显著的，反之则认为不显著。

2.2.2. Mann-Kendall检验法

Mann-Kendall检验法是世界气象组织推荐的一种非参数检验方法，在许多气象方面的研究都能看到Mann-Kendall方法的应用，尤其是在对降水、气温等气象要素时间序列的变化趋势分析方面。但本文利用Mann-Kendall法对时间序列进行突变分析并确定突变发生的时间，该方法的优点是样本不必遵从一定的分布，也不受少数异常值的干扰，并且该方法的计算比其他方法的计算更加简便。

通过构造序列：

$S_k={\displaystyle {\sum }_{i=1}^k{\displaystyle {\sum }_j^{i-1}{\alpha }_{ij}}}\left(k=2,3,4,\cdots ,n\right)$ (5)

其中，

${\alpha }_{ij}=\{\begin{array}{l}1x_i>x_j\\ 0x_i\le x_j\end{array}$, $1\le j\le i$ (6)

定义统计变量：

$U{F}_k=\frac{\left|S_k-E\left(S_k\right)\right|}{\sqrt{V\alpha \gamma \left(S_k\right)}}\left(k=1,2,\cdots ,n\right)$ (7)

式中 $E\left(S_k\right)$ 是 $S_k$ 的均值， $V\alpha \gamma \left(S_k\right)$ 是 $S_k$ 的方差，其表达式如下：

$E\left(S_k\right)=k\left(k-1\right)/4$ (8)

$V\alpha \gamma \left(S_k\right)=k\left(k-1\right)\left(2k+5\right)/72$ (9)

$U{F}_k$ 满足标准正态分布，在显著性水平 $\alpha$ 上，若 $\left|U{F}_k\right|>U_{\alpha }$，则表明序列存在明显的变化趋势，将时间序列x按逆序排列，再按照(1.7)式计算，得到 $U{B}_k$ ：

$\{\begin{array}{l}U{B}_k=-U{F}_k\\ k=n+1-k\end{array}\left(k=1,2,\cdots ,n\right)$ (10)

分析统计量 $U{F}_k$ 和 $U{B}_k$，可以找到突变点并明确突变的时间。若 $U{F}_k$ 值大于0，则表明序列呈上升趋势；若 $U{F}_k$ 值小于0则表明呈下降趋势；当它们超过临界直线时，表明其上升或下降的趋势显著。如果UF和UB这两条曲线在置信区间内相交，这个交点即突变点，而突变点对应的时刻就是突变发生的时刻 [18] [19] [20] [21]。

2.2.3. 小波分析

小波分析在分辨不同尺度上时间序列的演变特征方面是非常有效的。在一定的时间尺度下，小波系数能反映时间序列中所包含的某一时间尺度的周期震荡的强弱，而小波方差对应峰值处的尺度即为该序列的主要时间尺度，即主要周期。由此可判断该序列存在的主要周期并进行阶段分析。

定义一个小波函数：设 $\phi \left(t\right)$ 为一平方可积函数，即 $\phi \left(t\right)\in L^2\left(R\right)$，若其傅里叶变换 $\Psi \left(\omega \right)$ 满足容许条件：

$C_{\phi }={\displaystyle {\int }_R\frac{{\left|\Psi \left(\omega \right)\right|}^2}{\omega }\text{d}\omega }<+\infty$ (11)

则 $\phi \left(t\right)$ 称为一个基本小波或小波母函数，伸缩和平移小波函数 $\phi \left(t\right)$，就得到连续小波 ${\phi }_{a,\tau }\left(t\right)$ ：

${\phi }_{a,\tau }\left(t\right)=\frac{1}{\sqrt{a}}\phi \left(\frac{t-\tau }{a}\right),a,\tau \in R,a>0$ (12)

将连续小波变换(任意函数 $f\left(t\right)\in L^2\left(R\right)$ )定义为：

$W_f\left(a,\tau \right)=\langle f\left(t\right),{\phi }_{a,\tau }\left(t\right)\rangle =\frac{1}{\sqrt{a}}{\displaystyle {\int }_{R}f\left(t\right)\phi \left(\frac{t-\tau }{a}\right)\text{d}t}$ (13)

其中，a是尺度因子， $\tau$ 为平移因子， $W_f\left(a,\tau \right)$ 称为小波系数。本文的小波母函数是采用的Matlab小波分析工具箱中的Morlet小波，利用该小波对长江上游的气温资料进行连续小波变换。

引入小波方差：

$Wp\left(a\right)={\displaystyle {\int }_{-\infty }^{+\infty }{\left|W_f\left(a,\tau \right)\right|}^2\text{d}\tau }$ (14)

式中： $Wp\left(a\right)$ 为小波方差， $W_f\left(a,\tau \right)$ 为小波系数。由(1.11)式可知，小波方差能反映气温时间序列波动的能量随尺度因子a的分布情况 [22] [23] [24]。

3. 平均气温的空间分布特征

3.1. 空间分布特征

根据长江上游地区全年平均气温空间分布图发现(图2)：长江上游地区气温的空间分布差异明显，气温相差较大，东部和南部(华坪以及宜宾至宜昌的长江干流一带)是平均温度的高值区，最高可达20℃，长江源区包括沱沱河、五道梁等是长江上游最冷的区域，最低平均温度只有−5℃。同时理塘、稻城和峨眉相对其周边地区是一个相对低值中心，由此可见，长江上游平均气温自西北向东南逐渐升高。

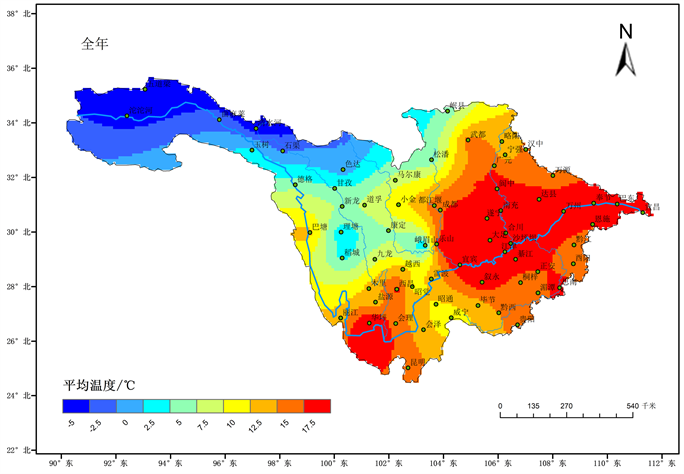
Figure 2. Spatial distribution of annual mean temperature (unit: ˚C) in the upper reaches of the Yangtze River

图2. 长江上游全年平均气温(单位：℃)空间分布图

由长江上游四季平均气温空间分布图(图3)可知，长江上游地区各季节多年平均气温的空间分布与全年的空间分布基本一致，自西北向东南，平均温度逐渐升高，其中夏季最高温度可达28℃，冬季最低温度为−16℃，春秋季的平均温度范围相差不大，处于−4℃~16℃之间。

Figure 3. Spatial distribution of average temperature in spring (a), Summer (b), Autumn (c) and Winter (d) over the upper reaches of the Yangtze River

图3. 长江上游(a) 春季、(b) 夏季、(c) 秋季、(d) 冬季平均气温(单位：℃)空间分布图

由各年代平均气温分布图(图4)可知，总体而言，20世纪60年代至21世纪10年代是一个升温的过程。具体来说，20世纪60~80年代是一个降温过程，80~90年代处于波动调整阶段，90年代后开始快速升温。

从图上可以看出20世纪60~80年代最低温度的分布范围几乎没有变化，而最高温度的分布范围明显减小。80~90年代最高温度的分布范围开始扩大，但变化不明显，90年代后，最高温度的分布范围明显增加，90年代高温区仅位于宜宾、江津、沙坪坝地区，而21世纪10年代已经延伸到万州、奉节一带，并且就最低温度而言，20世纪90年代的最低温度处于−6℃~−5℃之间，而21世纪10年代的最低温度已经上升到−4℃以上，升高了近2℃，说明20世纪90年代至21世纪10年代的平均温度整体上升明显。

Figure 4. Spatial distribution of mean temperature (unit: ˚C) in the upper reaches of the Yangtze River in (a) 1960s, (b) 1970s, (c) 1980s, (d) 1990s; (e) 2000s and (f) 10s

图4. 长江上游(a) 60年代、(b) 70年代、(c) 80年代、(d) 90年代、(e) 00年代、(f) 10年代平均气温(单位：℃)空间分布图

3.2. 变化趋势空间分布特征

如图5所示，长江上游地区平均气温变化趋势空间差异明显，并且在所选的68个站点中有56个站点均通过了显著性水平为0.05的显著性检验。长江上游区域平均气温的升温一致性较好，中部和西部显著上升，而东南部呈显著下降趋势，升温幅度从西北向东南方向逐渐减弱。长江源区和金沙江水系区域升温幅度最大，其气温变化率介于0.3~0.6℃/10a。

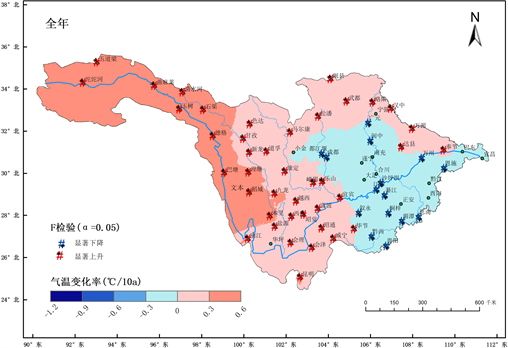
Figure 5. Spatial distribution of annual mean temperature trend (unit: ˚C/10a) in the upper reaches of the Yangtze River

图5. 长江上游全年平均气温变化趋势(单位：℃/10a)空间分布图

由各季节的变化趋势空间分布图(图6)分析可得，春季，长江上游地区除了理塘和武都外，均呈现上升趋势，且其中有48个站点通过显著性检验，大部分地区气温变化率介于0~0.3℃/10a之间，整体升温幅度较小，其中高值中心为木里，达到了0.694℃/10a。理塘和武都两地是气温变化的两大低值中心，其气温变化率分别为−0.889℃/10a和−0.811℃/10a，但没有通过显著性水平为0.05的显著性检验，表明这两个站点的变化趋势不显著。

夏季，长江上游地区平均气温在东北部呈下降趋势，中部和东部气温上升，且中部升温幅度最大。在呈下降趋势的站点中只有岷县、武都、沙坪坝、万州、奉节和巴东通过了显著性检验，其余地区下降趋势不显著；而呈上升趋势的站点只有少数未通过显著性检验，其中木里升温幅度达到了0.616℃/10a。

秋季，长江上游大部分地区平均气温均呈现上升趋势，且大部分站点气温上升显著。曲麻莱和巴塘是气温变化的两大低值区，其气温变化率分别为−1.124℃/10a和−0.725℃/10a，但未通过显著性检验，升温幅度最大的依旧是木里，达到了0.713℃/10a。

冬季的气温变化趋势分布与全年的分布一致，金沙江流域升温显著，其中升温幅度最大的是木里，达到0.926℃/10a。

Figure 6. Spatial distribution of average temperature variation trend (unit: ˚C/10a) in Spring (a), Summer (b), Autumn (c) and Winter (d) over the upper reaches of Yangtze River

图6. 长江上游(a) 春季、(b) 夏季、(c) 秋季、(d) 冬季平均气温变化趋势(单位：℃/10a)空间分布图

4. 平均气温的时间变化特征

如图7所示，近60年来，长江上游地区的多年平均气温为12.1℃，整体呈现上升趋势，其增温率为0.194℃/10a，并通过了显著性水平为0.05的F检验，表明在0.05的显著性水平下有统计显著性，同时由图7可知，21世纪00年代增温幅度最大，全年平均气温的最大值为13.11℃ (2006年)，最小值为11.36℃ (1968年)。

分析四季的平均气温曲线图(图8)可以得知，春、夏、秋、冬四季的平均气温也呈现明显的上升趋势，其中冬季的上升趋势最为显著，其次是秋季。春、夏、秋、冬四季的多年平均气温依次是12.60℃、20.25℃、12.48℃、3.11℃，显而易见，冬季的多年平均气温较其他三个季节低，但其变暖趋势比其他三个季节明显，并且其增幅最大，达0.245℃/10a，大于全年的增幅。秋季的升温幅度仅次于冬季，其升温率为0.2℃/10a，同样略大于全年增幅。由此可以得出，秋冬季是长江上游年平均气温上升的主要贡献者。春夏季的多年平均气温较高，夏季多年平均气温的最大值达到了21.72℃ (2013年)，春季最大值为13.89℃ (2018年)，但是这两个季节增温趋势都较弱，并且在1980~1987年整体平均气温都是下降的，之后才出现缓慢持续的升温。

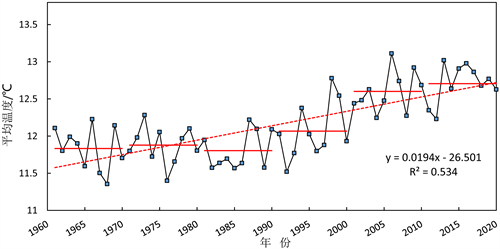
Figure 7. Curve of annual mean temperature (unit: ˚C) in the upper reaches of the Yangtze River (black broken line is annual mean temperature, red solid line is decadal mean temperature, and red dotted line is trend line)

图7. 长江上游全年年平均气温(单位：℃)变化曲线图(黑色折线为年平均温度、红色实线为年代平均温度、红色虚线为趋势线)

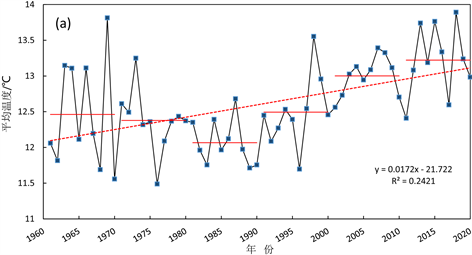
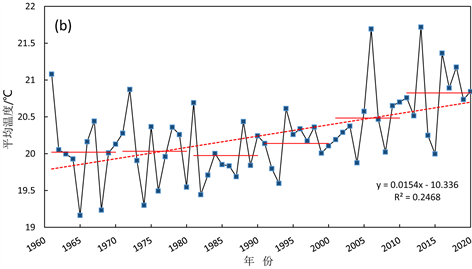
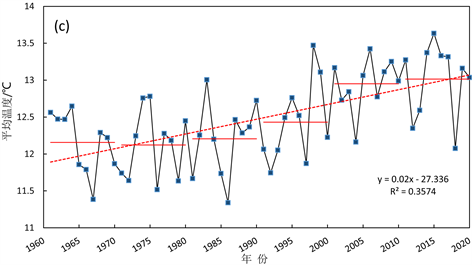
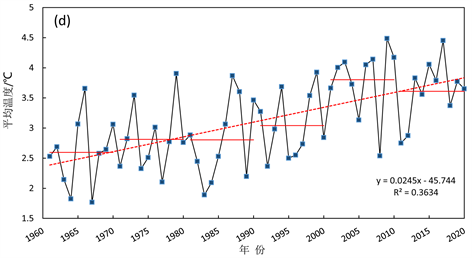
Figure 8. Curve of annual mean temperature (unit: ˚C) in Spring (a), Summer (b), Autumn (c) and Winter (d) over the upper reaches of the Yangtze River (black broken line is annual mean temperature, solid red line is decadal mean temperature, and red dotted line is trend line)

图8. 长江上游(a) 春季、(b) 夏季、(c) 秋季、(d) 冬季年平均气温(单位：℃)变化曲线图(黑色折线为年平均温度、红色实线为年代平均温度、红色虚线为趋势线)

5. M-K突变检验分析

长江上游年平均气温的M-K突变检验结果(图9)显示该区域总体呈现先下降后上升的变化趋势，

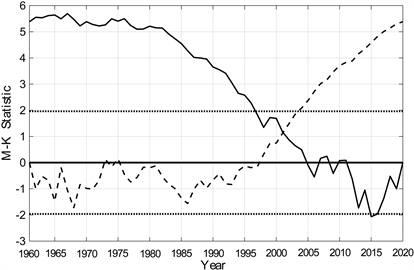
Figure 9. M-K mutation test of annual mean temperature in the upper reaches of the Yangtze River (the black solid line is UB, the dotted line is UF, and the dotted line is α₉₅ = ±1.96 critical line)

图9. 长江上游全年平均气温M-K突变检验(黑色实线为UB、虚线为UF、点线为α₉₅ = ±1.96临界直线)

1997年以前，UF小于0，气温下降，1997年之后气温开始回升，在2001年UF统计量和UB统计量在0.95的置信水平下相交，交点在置信区间内，说明长江上游地区平均气温在2001年发生突变。而在2004年，UF开始超出置信区间，升温趋势变得显著。

由图10可知，长江上游地区各季节的平均气温均存在突变。在1975年以前，春季气温波动上升，1976~1998年气温逐渐下降，随后又出现升温过程。突变开始的时间为2003年，2007年春季平均气温开始呈现显著上升的趋势。

夏季，长江上游平均气温在1996年之前气温大体呈下降趋势，其中1964~1966年的下降趋势显著，1996年之后，气温逐渐上升，在2005年气温开始突变，2009年UF统计量超出置信区间，气温的上升趋势逐渐显著。

秋季，长江上游的平均气温在1961~1994年呈现出下降的趋势，该趋势在1970~1973年是显著的。从图中可以看出，1998年平均气温发生了突变，加速上升，在2005年上升趋势变得显著。

冬季，平均气温在1967年之前波动变化，在1967年之后大体呈现上升趋势。1997年，气温开始发生突变，在2001年之后，升温趋势愈加显著。

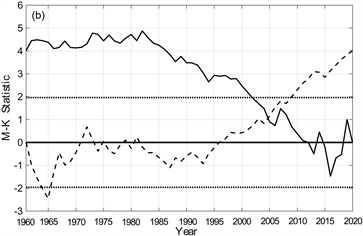
Figure 10. M-K mutation test of mean temperature in (a) Spring, (b) Summer, (c) Autumn and (d) Winter over the upper reaches of the Yangtze River (the black solid line is UB, the dotted line is UF, and the dotted line is α₉₅ = ±1.96 critical line)

图10. 长江上游(a) 春季、(b) 夏季、(c) 秋季、(d) 冬季平均气温M-K突变检验(黑色实线为UB、虚线为UF、点线为α₉₅ = ±1.96临界直线)

6. Morlet小波分析

本文采用Morlet小波分析法对长江上游的全年平均气温和四季平均气温进行周期性检验，绘制了长江上游全年平均气温和四季平均气温的小波变换系数实部等值线图(图11和图12)，小波系数的大小表示信号的强弱，图中红色表示正相位，即气温偏暖；蓝色表示负相位，即气温偏冷。为了进一步分析气温变化的周期规律，绘制了夏季和冬季平均气温的小波方差图(图13)。

图11可知，长江上游平均气温在55~60a的时间尺度上周期震荡明显，呈上升–下降–上升的交替循环，并且在2020年后不久等值线即将闭合，预计未来2020年长江上游地区平均气温将下降，其次在3 a的时间尺度上，年平均气温也存在弱周期变化，主要发生在1988~2013年。

Figure 11. Real part contour map of wavelet coefficients of mean temperature in the upper Reaches of the Yangtze River

图11. 长江上游平均气温小波系数实部等值线图

图12(a)表明，春季平均气温在时间尺度为50~60 a上，出现上升–下降–上升的循环并较为显著，除此之外，年平均气温在5~10年的时间尺度上也存在弱周期变化，但没有50~60 a时间尺度的震荡明显。

从图12(b)发现，夏季，同样在50~55 a的时间尺度上，平均气温的周期震荡明显，依旧出现上升–下降–上升的周期循环，同时在3~10 a的时间尺度里，年平均气温的周期变化也较为清晰，以3 a为周期的变化主要发生在1961~1983年和2003~2018年，以6 a为周期的变化主要发生在1960~1977年，以10 a为周期的变化主要发生在1960~1985年。

由图12(c)可知，长江上游秋季平均气温在5 a、55~60 a的时间尺度上都存在较明显变化，其中以5 a为周期的变化主要发生在1965~2000年，而在55~60 a时间尺度上的变化与春、夏季的变化基本一致。小波系数等值线在2020年接近闭合，说明2020年后将存在一个缓慢持续的降温过程。

分析图12(d)可知，冬季长江上游平均气温的周期变化较春夏秋季更加显著，以下3个时间尺度上的周期震荡都较为明显：8、15、60 a，当时间尺度为8 a时，其周期变化主要发生在1963~1993年；当时间尺度为15 a时，其周期变化主要发生在1980~2020年；当时间尺度为60 a时，其周期变化主要发生在1963~2020年。

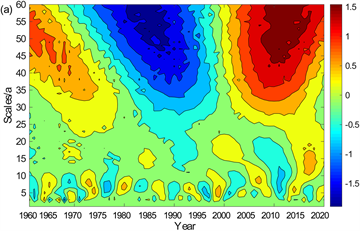
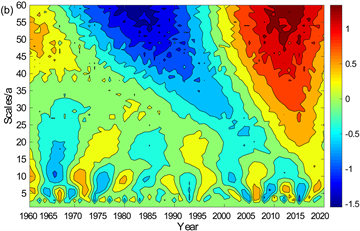
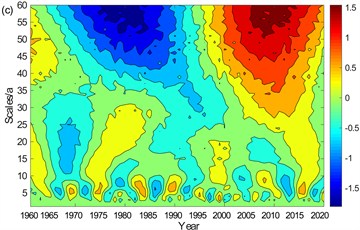
Figure 12. Real part contour maps of wavelet coefficients of mean temperature in (a) Spring, (b) Summer, (c) Autumn and (d) Winter over the upper reaches of the Yangtze River

图12. 长江上游(a) 春季、(b) 夏季、(c) 秋季、(d) 冬季平均气温小波系数实部等值线图

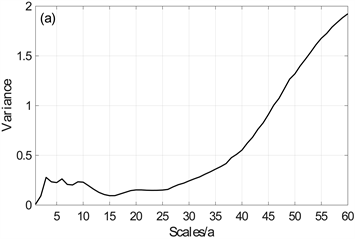
Figure 13. Wavelet square difference of mean temperature in (a) Summer and (b) Winter in the upper reaches of the Yangtze River

图13. 长江上游(a) 夏季、(b) 冬季平均气温小波方差图

根据小波方差图(图13)可以看出：夏季和冬季，小波方差最大值对应的时间尺度为60 a，其次是59 a和58 a，除了上述震荡比较明显的3个时间尺度外，小波方差在时间尺度3 a、6~7 a和10~15 a上有极值，说明夏季和冬季年平均气温在3 a、6~7 a和10~15 a时间尺度存在一定的周期变化。

7. 结论

结合长江上游地区1961~2020年68个气象站点的逐日日平均气温数据资料，主要利用M-K突变检验和Morlet小波分析方法，对长江上游平均气温的时间变化趋势、空间分布、突变检验和变化周期进行了研究，得出了如下结论：

1) 长江上游地区平均气温的空间分布差异较大，平均气温自西北向东南方向逐渐升高。在变化趋势空间分布方面，长江上游地区升温一致性较好，升温幅度从西北向东南方向逐渐减弱，其中长江源区和金沙江水系区域升温幅度最大。

2) 长江上游地区1961~2020年的多年平均气温为12.1℃，整体呈现上升趋势，增温率为0.194℃/10a，并且21世纪00年代增温幅度最大。通过季节对比发现秋冬季增温较春夏季增温显著，表明秋冬季平均气温的上升对长江上游平均气温的上升有主要贡献。

3) 从突变特征来看，长江上游地区平均气温在2001年发生突变，2004年之后升温显著；四季平均气温突变时间依次为2003、2005、1998、1997年前后，其中秋冬季突变时间早于春夏季，说明秋冬季的增温贡献大于春夏季。从变化周期来看，近60年长江上游地区夏季和冬季的平均温度在3 a、6~7 a和10~15 a的时间尺度上存在周期变化。

参考文献