1. 引言
高聚物薄膜因其良好的性能在材料加工技术不断发展的今天得到了广泛的关注,构建基于高聚物非牛顿流体的流变学特质的本构关系,用来描述非牛顿流体的流动传热传质行为具有重要研究价值。Chen [1] 研究了非稳态拉伸板上的非牛顿流体薄膜的流动和传热。粘弹性流体是最常见的非牛顿流体之一,其中最简单的粘弹性流体是具有松弛时间效应的Maxwell流体。起初,Khan [2] 研究了收缩和拉伸板上Maxwell流体的薄膜流动。Hayat等人 [3] 运用同伦分析方法(HAM)得到了上随体Maxwell磁流体通过多孔收缩板边界层流动的解析解。随后,Nadeem等人 [4] 用数值方法考虑了Maxwell磁流体的边界层流动。进一步,Hayat等人 [5] 分析了Maxwell流体的三维边界层流动和传热行为,Zhang [6] 利用韦兰胶溶液的流变学实验,建立了能同时描述剪切变薄和粘弹性的Maxwell-幂律本构方程,讨论了以非稳态拉伸板为界的变化厚度的Maxwell-幂律流体的流动传热性质。
研究表明,在聚合物中添加纳米粒子可有效提高材料的导热性能。纳米流体作为一种新的换热基质,在化工、能源、航天航空等领域都发挥了巨大作用。纳米流体的概念由Choi [7] 在1995年首次提出,Fakour [8] 与Li [9] 等人对非稳态拉伸平板上的牛顿纳米流体薄膜的流动与传热进行了研究,Malvandi [10] 提出了有关粘弹性纳米流体薄膜流动的数学模型。然而,有关Maxwell-幂律纳米流体的传热特征至今还未见研究。
实际上,对于热固表面存在有热量交换,Hayat [11] 与Nayak [12] 等人研究了在对流换热边界条件下的纳米流体的传热。随后,Qayyum [13] 等人在对流换热边界中考虑到与位置相关的对流换热系数,讨论了Jeffrey纳米流体的流动传热问题。Khalili [14] 与Eid [15] 等人考虑到与时空相关的对流换热系数,研究了幂律纳米流体的流动传热问题。如何结合非傅里叶导热定律修正对流换热边界条件仍有待研究。
在通常情况下,流体并不粘附于固体边界,称之为速度滑移。通过实验 [16] [17] 与理论分析 [18] 可以证明在固液壁面之间存在速度滑移。Beavers and Joseph [19] 提出了一种滑移边界条件,Andersson [20] 研究了拉伸表面上的滑移流动,Seth与Mishra [21] 以及Noghrehabadi [22] 等人分析了在Navier速度滑移作用下牛顿纳米流体的边界层流动问题,Nandy [23] 讨论了可渗透拉伸板上具有Navier速度滑移的Maxwell纳米流体的非稳态流动。然而,上述非牛顿流体滑移速度的表达式仍基于牛顿流体本构方程得到的。
针对以上研究存在的问题,本文建立了可渗透拉伸板上Maxwell-幂律流体的流动传热边界层控制方程。采用相似变换将偏微分方程转化为常微分方程,并且利用双参数变形展开方法(DPTEM)进行求解。通过图形分析了戴博拉数、磁场参数、纳米粒子的体积分数等对膜厚、速度场和温度场的影响。
2. 模型建立
根据流变学实验已经证实了韦兰胶水溶液符合Maxwell-幂律本构 [6]。为提高导热性能,在韦兰胶溶液中加入SiO2纳米粒子,制备Maxwell-幂律纳米流体,相关物性参数见表1。考虑可渗透拉伸板上Maxwell-幂律纳米流体薄膜的流动传热问题。假定拉伸板以笛卡尔坐标原点为起点,物理模型如图1所示。

Table 1. Related physical parameters of base fluid and nanoparticles
表1. 基液和纳米粒子的相关物性参数
可渗透拉伸板以uw = bx的速度沿x轴方向从窄缝中拉出,拉伸板温度为
,其中T0是窄缝温度,Tref是正常参考温度,b为拉伸速率,d是一个常数。y轴垂直于拉伸板的方向。考虑磁场效应对流体速度的影响。
Maxwell-幂律本构方程为:
(1)
其中λ表示松弛时间参数,S是应力张量,μ表示流体的粘度系数,
是剪切速率,A为里夫林–埃里克森张量,
表示上随体导数。
根据质量守恒、动量守恒定律,可得如下连续性方程和Maxwell-幂律流体的动量方程:
(2)
(3)
其中u和v分别表示流体在x和y方向上的速度分量,μnf表示纳米流体粘度,ρnf表示纳米流体密度,σ表示电导率,B表示磁场。
依据动量守恒与能量守恒的比拟原理,引入如下具有幂律导热系数的Cattaneo-Christov热通量模型 [24]:
(4)
式中λE表示热松弛时间参数,q表示热通量向量,k为导热参数,T为温度。忽略粘性耗散,可以得到如下能量方程:
(5)
根据Maxwell-幂律本构方程以及Navier滑移的定义,在壁面y = 0处,修正的速度滑移边界条件为:
(6)
其中λ1为滑移参数。
壁面y = 0处的吸入速度为:
(7)
在薄膜上表面y = h(x)处的速度满足如下条件:
(8)
在壁面y = 0处存在对流换热,基于具有幂律导热系数的Cattaneo-Christov热通量模型,修正后的对流换热边界条件为:
(9)
其中αnf表示纳米流体的热扩散系数。
在薄膜上表面y = h(x)处没有对流换热,相应的边界条件为:
(10)
为将控制方程转化为无量纲的常微分方程组,引入如下流函数和相似变换:
其中β是无量纲的薄膜厚度,将相似变换代入偏微分控制方程和边界条件中,得到速度和温度的常微分控制方程组:
(11)
(12)
其中:
对应的边界条件转化为:
当
时:
(13)
当
时:
其中:
其中
表示纳米流体的体积分数,ρ表示密度,ρCp表示热容量,α表示热扩散系数,下标f,s和nf分别代表流体基液,纳米颗粒和纳米流体,S表示渗透参数,
和
分别表示松弛时间和热松弛时间的戴博拉数,
是普朗特数,Bi是比渥数。
3. DPTEM方法求解
采用双参数变形展开的方法 [25] 求解具有边界条件(13)的常微分方程组(11)~(12)。假设:
(14)
其中a和b表示未知常数,常微分方程中的自变量和因变量可以转化为:
(15)
(16)
(17)
其中
是小参数,
为无量纲自变量,
是关于
的未知函数。
将
在
附近展开成幂级数形式:
(18)
(19)
对应的边界条件为:
(20)
(21)
将方程(20)~(21)代入方程(18)~(19),得到如下初值条件:
(22)
(23)
将方程(15)~(19)代入方程(11)~(12)中,对比ε相同次幂前的系数,根据多项式性质,使系数等于零,可以得到一系列常微分方程,根据初值条件(22)~(23)可以得到
的表达式,进而得到
的表达式,根据方程(15)~(17),可以得到
的表达式。根据边界条件(13)确定常数a和b的值。
4. 结果与讨论
采用双参数变形展开的方法得到了微分方程的近似解析解。并且,通过图形分析了各物性参数对速度场和温度场的影响。
图2给出了戴博拉数De对速度场的影响,由图2可知,随着De的增加流体速度增加,膜厚减小。

Figure 2. Influence of De on the velocity field
图2. De对速度的影响
图3显示了磁场参数M对速度的影响,随着M的增大,在磁场作用下的洛伦兹力阻碍了流体的流动,流动速度减小。

Figure 3. Influence of M on the velocity field
图3. M对速度的影响
图4反映了渗透参数S变化时对速度的影响,随着S的减小,流体在重力作用下的动量越小,流体的流速也随之减小。渗透能力越强,膜厚越薄。

Figure 4. Influence of S on the velocity field
图4. S对速度的影响
图5揭示了戴博拉数DeE对温度场的影响,DeE的增加有助于流体温度的升高,但对膜厚的影响很微弱。
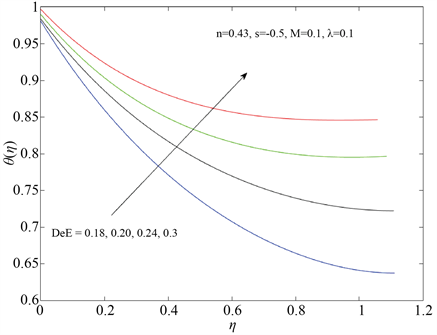
Figure 5. Influence of DeE on the temperature field
图5. DeE对温度的影响
图6表明了纳米粒子的体积分数对温度场的影响,随着体积分数的增大,温度也随之增加,这是由于在靠近薄膜上表面时,θ(η)是参数
的增函数,而在薄膜上表面的对流换热影响很小,所以温度会呈现增加的趋势。

Figure 6. Influence of
on the temperature field
图6.
对温度的影响
5. 总结
本文针对具有Maxwell-幂律本构的流体考虑了相应的速度滑移及对流换热边界条件来描述其流动传热行为,并且利用巧妙的相似变换将控制方程转化为常微分方程,结合双参数变形展开方法与基函数方法(DPTEM-BF)进行求解。De、M和S对膜厚影响十分显著,而DeE和
对膜厚几乎没有影响。增大De和S有助于流体的流动,增大DeE和
有助于增强传热效果。
基金项目
国家自然科学基金项目(No. 12102032),北京市自然科学基金–北京市教委联合项目基金(KZ201810016018),北京建筑大学青年教师科研能力提升计划(X21027)。
NOTES
*通讯作者。