基于GM(1,1)模型的秦皇岛市老龄化程度预测

Prediction of Aging Degree in Qinhuangdao City Based on the GM(1,1) Model

摘要: 2019年，秦皇岛市60岁以上老年人口有69.68万人，占总人口的23.12%，高于全国、全省的平均水平，老龄化问题非常明显。本文利用2010~2019年秦皇岛市60岁以上老年人口及总人口数据，运用灰色GM(1,1)模型，分别预测了2020~2030年秦皇岛市60岁以上老年人口数及老龄化系数。预测结果表明未来十年秦皇岛市60岁以上老年人口数量将依然保持逐年上升，老龄化系数同时也在持续上涨。最后，从预测结果出发，为秦皇岛市进入老龄化社会后相关部门制定相关政策提供建议。

Abstract: In 2019, there were more than 690 thousand people over 60 years old in Qinhuangdao, which accounts for 23.12% of the total population and is higher than the national and provincial average level. And the aging problem is very obvious. Based on the data of the elderly population over 60 years old and the total population in Qinhuangdao city from 2010 to 2019, using the grey GM(1,1) model prediction methods, this paper forecasts the number of the elderly population over 60 years old and the aging coefficient in Qinhuangdao city from 2020 to 2030. The prediction results show that the number of people over 60 years old in Qinhuangdao will increase year by year in the next decade, and the aging coefficient will also continue to rise. Finally, this paper provides suggestions for relevant departments to formulate relevant policies after Qinhuangdao enters an aging society based on the prediction results.

1. 引言

人口老龄化与社会可持续性发展已经成为备受关注的两大世界性问题。其中人口老龄化与社会经济发展有着密切关系，老龄人口增多将带来劳动力减少、社会保障费用增加、养老需求过高、经济发展缓慢等显著问题。

如何判断一个社会处于老年型社会，目前国际上的标准是，当地60岁以上的老年人口数目占该地区人口总数目的10%，或65岁以上的老年人口数目占该地区人口总数目的7% [1]。

灰色系统理论最早由我国学者邓聚龙于1982年提出，目前使用最广泛的灰色系统模型是用于1阶、1个变量的GM(1,1)模型，与其他模型相比，GM(1,1)模型简单，只需要较小的数据量就可以较好地预测中短期人口，而且由于灰色系统本身的良好特性，模型中可以含有未知信息，国内学者在预测中短期人口数量时也会优先选择GM(1,1)模型。王泽旻 [2] 将GM(1,1)模型应用于我国人口数量研究之中，预测了未来10年我国人口数目的变化；谭春英 [3]、王莉 [4]、高红 [5] 分别用GM(1,1)模型对未来烟台市、厦门市、南京市的人口规模进行预测，并都取得了良好的效果。

地处人口大省——河北省的秦皇岛市，2019年的常住人口中60岁及以上人口数量已经达到了69.68万人，占比高达23.12%，远远超过了当年全国平均老龄化水平18.1%。且秦皇岛市家庭不断小型化，农村劳动力不断向城市转移，社会抚养负担日益加重，研究秦皇岛市人口老龄化问题，预测未来秦皇岛市老年人口数量，为秦皇岛市进入老年型社会后相关部门制定相关政策提供数据支持，提出有助于秦皇岛市养老产业发展的建议有着重要的现实意义。本研究将根据秦皇岛市人口数据的灰白不确定性特点，通过建立GM(1,1)模型预测秦皇岛市未来短期老龄化程度。

2. 人口预测模型的建立和结果

2.1. 数据检验与处理

从《秦皇岛市统计年鉴》中获得2010~2019年秦皇岛市总人口及60岁以上人口数据，计算得出2010~2019年秦皇岛市老龄化系数的数据，如表1所示。

在建立GM(1,1)模型之前，首先需要对秦皇岛市2010~2019年60岁以上人口数量及老龄化系数数据进行级比检验，分别计算两个数列的级比。记原始序列为 $X^{\left(0\right)}\left(t\right),t=1,2,\cdots ,n$，根据级比公式

$\sigma \left(t\right)=\frac{X^{\left(0\right)}\left(t-1\right)}{X^{\left(0\right)}\left(t\right)},t=2,3,\cdots ,n$，计算出两个序列的级比 $\sigma \left(t\right)$ 均符合 $\sigma \left(t\right)\in \left({\text{e}}^{-\frac{2}{n+1}},{\text{e}}^{\frac{2}{n+1}}\right)=\left(0.833,1.199\right)$，所有的级比都落在了可容覆盖区间内，说明两个原始数据序列均满足灰色预测模型的级比判断条件。所以可以对秦皇岛市2010~2019年60岁以上人口数量及老龄化系数构建灰色GM(1,1)模型，且可以进行灰色预测。

Table 1. Statistical table of population aged over 60 and aging coefficient of Qinhuangdao city from 2010 to 2019

表1. 2010~2019年秦皇岛市60岁及以上人口和老龄化系数统计表

2.2. 模型建立

由表1可得秦皇岛市2010~2019年60岁以上人口数量序列：

$\begin{array}{c}{X}^{\left(0\right)}=\left\{X^{\left(0\right)}\left(1\right),X^{\left(0\right)}\left(2\right),\cdots ,X^{\left(0\right)}\left(n\right)\right\}\\ =\left\{403235,456164,500159,527168,555306,590404,608476,641777,674177,696756\right\}\end{array}$

对 $X^{\left(0\right)}$ 进行一次累加(通过累加的过程可以使灰色过程由灰变白)，得到一阶累加生成序列：

$X^{\left(1\right)}\left(t\right)={\displaystyle \underset{i=1}{\overset{t}{\sum }}{X}^{\left(0\right)}}\left(i\right),t=1,2,\cdots ,n$

记 $X^{\left(1\right)}=\left\{X^{\left(1\right)}\left(1\right),X^{\left(1\right)}\left(2\right),\cdots ,X^{\left(1\right)}\left(n\right)\right\}$，则有

$X^{\left(1\right)}=\left\{403235,859399,1359558,1886726,2442032,3032436,3640912,4282689,4956866,5653622\right\}$。

GM(1,1)模型的灰微分方程基本形式为

$X^{\left(0\right)}\left(t\right)+a{Z}^{\left(1\right)}\left(t\right)=u$，

其中， $Z^{\left(1\right)}\left(k\right)$ 为累加序列 $X^{\left(1\right)}$ 的紧邻均值生成序列， $Z^{\left(1\right)}\left(t\right)=-\frac{1}{2}\left(X^{\left(1\right)}\left(t-1\right)+X^{\left(1\right)}\left(t\right)\right),t=2,3,\cdots ,n$，a为发展系数，反映原始序列及累加序列的发展态势，u为灰色作用量，反映数据变化的关系 [6]。

记参数列 $\hat{a}={\left[a,u\right]}^{\text{T}}$， $B=\left[\begin{array}{cc}-\frac{1}{2}\left(X^{\left(1\right)}\left(1\right)+X^{\left(1\right)}\left(2\right)\right)& 1\\ -\frac{1}{2}\left(X^{\left(1\right)}\left(2\right)+X^{\left(1\right)}\left(3\right)\right)& 1\\ ⋮& ⋮\\ -\frac{1}{2}\left(X^{\left(1\right)}\left(n-1\right)+X^{\left(1\right)}\left(n\right)\right)& 1\end{array}\right]$， $Y=\left(\begin{array}{c}{X}^{\left(0\right)}\left(2\right)\\ X^{\left(0\right)}\left(3\right)\\ ⋮\\ X^{\left(0\right)}\left(n\right)\end{array}\right)$，则可以应用最小二乘估计法计算出 $\hat{a}={\left[a,u\right]}^{\text{T}}={\left(B^{\text{T}}B\right)}^{-1}{B}^{\text{T}}Y={\left[-0.05011,441467.95781\right]}^{\text{T}}$。

GM(1,1)模型相对应的白化方程形式为：

$\frac{\text{d}{X}^{\left(1\right)}\left(t\right)}{\text{d}t}+a{X}^{\left(1\right)}\left(t\right)=u$，

求解微分方程即可得到时间响应函数序列为：

${\hat{X}}^{\left(1\right)}\left(t+1\right)=\left(X^{\left(0\right)}\left(1\right)-\frac{u}{a}\right){\text{e}}^{-at}+\frac{u}{a}=9213769{\text{e}}^{0.05011t}-8810534,t=1,2,\cdots ,10$。

类似的，以计算出的秦皇岛市2010-2019年老龄化系数为原始序列 $X^{\left(0\right)}$ 建立灰色GM(1,1)模型，最终得到的预测模型为：

$X^{(1)}(t+1)=351.2493e^{0.04539t}-337.259,t=1,2,\cdots ,10$。

2.3. 模型检验

为了判断建立的模型是否可以真实地反映秦皇岛市老龄化情况，需要对建立的模型进行模型精度检验。常用的GM(1,1)模型精度检验方法为相对误差检验和和后验差检验。

1) 相对误差检验

相对误差的计算公式为： $\epsilon \left(t\right)=\frac{|X^{\left(0\right)}\left(t\right)-{\hat{X}}^{\left(0\right)}\left(t\right)|}{X^{\left(0\right)}\left(t\right)},t=1,2,\cdots ,n$。

Table 2. Prediction value and relative error of Grey GM(1,1) model for elderly population

表2. 老年人口灰色GM(1,1)模型预测值及相对误差

根据数据计算出的老年人口数量预测值和相对误差如表2所示，可以看出利用建立的GM(1,1)模型得出的秦皇岛市60岁以上人口数量预测值与实际值误差小，相对误差均小于5%，平均相对误差1.004%，说明模型拟合效果较好，预测精度较高，预测结果可靠性较强。

根据数据计算出的老龄化系数预测值和相对误差见表3。从表3中可以看出，对秦皇岛市老龄化系

Table 3. Prediction value and relative error of Grey GM(1,1) model for aging coefficient

表3. 老龄化系数GM(1,1)模型预测值及相对误差

数建立的GM(1,1)模型得出的老龄化系数预测值也与实际值误差小，相对误差也均小于5%，平均相对误差0.998%，说明模型拟合效果也较好，预测精度较高，预测结果可靠性较强。

2) 后验差检验

原始序列标准差： $S_1=\sqrt{\frac{{\displaystyle \sum {\left[X^{\left(0\right)}\left(t\right)-{\bar{X}}^{\left(0\right)}\right]}^2}}{n-1}}$ ；

绝对误差序列标准差： $S_2=\sqrt{\frac{{\displaystyle \sum {\left[e\left(t\right)-\bar{e}\right]}^2}}{n-1}}$，其中 $\bar{e}=\frac{1}{n}{\displaystyle \underset{t=1}{\overset{n}{\sum }}e\left(t\right)}$ ；

后验差比值： $C=\frac{S_2}{S_1}$ ；

小误差概率： $P=P\left\{|e\left(t\right)-\bar{e}|<0.6745S_1\right\}$。

一般来说，计算得到的后验差比值C的值越小，小误差概率值P的值越大，则模型精度越好。具体模型精度等级的具体划分标准见表4。

Table 4. GM(1,1) model test accuracy standard

表4. GM(1,1)模型检验精度等级划分标准

利用MATLAB软件可以计算出建立的秦皇岛市60岁以上人口数量GM(1,1)模型的后验值比差 $C=0.0003<0.35$，小误差概率值 $P=1>0.095$ ；秦皇岛市老龄化系数GM(1,1)模型的后验值比差 $C=0.0002<0.35$，小误差概率值 $P=1>0.095$，按照GM(1,1)模型精度等级划分标准，说明建立的两个模型预测等级为好，模型预测的结果可信度高，可以用这两个模型对秦皇岛市未来老年人口数量及老龄化系数进行预测。

2.4. 预测结果

基于上述过程建立的GM(1,1)模型，可以预测出2020~2030年秦皇岛市60岁以上人口数和老龄化系数，预测结果如表5所示，模型预测的走势图分别如图1、图2所示。

Table 5. Prediction of population aged over 60 and aging coefficient in Qinhuangdao from 2020 to 2030

表5. 2020~2030年秦皇岛市60岁及以上人口数量和老龄化系数预测

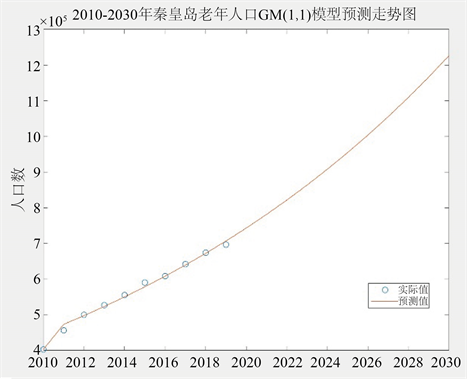
Figure 1. Forecast trend of GM(1,1) model for elderly population in Qinhuangdao from 2010 to 2030

图1. 2010~2030年秦皇岛老年人口GM(1,1)模型预测走势图

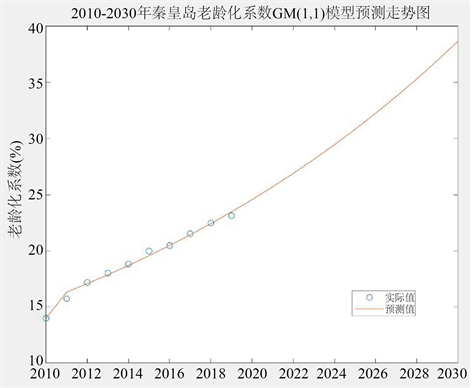
Figure 2. Forecast trend of GM(1,1) model for aging coefficient in Qinhuangdao from 2010 to 2030

图2. 2010~2030年秦皇岛老龄化系数GM(1,1)模型预测走势图

3. 结论与建议

本论文根据2010~2019年秦皇岛市总人口及60岁以上人口数据建立了秦皇岛60岁以上人口数量和老龄化系数的GM(1,1)模型，并对秦皇岛市2020~2030年的老龄人口数及老龄化系数进行了预测，模型对于数据量要求较小，通过相对误差检验和后验差检验，得到模型预测精度较高，具有较强的可靠性和可信度的结果。GM(1,1)预测模型可以对不确定系统整体变化进行动态科学仿真。因此建立的GM(1,1)预测模型的预测结果可以为秦皇岛市未来城市规划提供科学依据。

根据上文的GM(1,1)模型预测结果可以看出，到2030年秦皇岛市60岁以上的老年人口数量从2010年的40.32万人增长到了122.66万人，老龄化系数更是从2010年的13.99%迅速增长到了38.65%。而且未来10年中老龄化系数将逐年递增，增速逐渐加快，老龄化趋势日益加剧。老龄政策的制定应建立在对老龄化过程、前景的科学认识之上 [7]，所以，我们应该重视秦皇岛市的老龄化问题，实施合理有效的政策和措施减缓老龄化程度，解决因老龄化产生的种种问题。

1) 结合秦皇岛市情，建立健全社会养老体系。

老年人口日益增多，老年卫生服务问题矛盾也将凸显。为进一步提升老年医疗卫生服务水平，可以与京津医疗协作，推进北戴河国际健康城等特色医疗设施建设，引领医疗与养老、保健、旅游等相关领域的协同发展 [8]。同时需要继续完善社会医疗保险制度，争取实现形成全市全方位的社会养老保障体系。

2) 积极调整产业结构，推动秦皇岛市养老服务业发展。

秦皇岛市自然环境优越，生态气候良好，本市老龄化程度日益增高，且需要承担周边京津地区部分养老压力，需要尽快发展养老服务业，继续建设居家、社区相协调、医养康养相结合的养老服务业发展体系 [9]。另外，可以将关注点也放在老年人口的消费市场上，更好地满足老年人的衣、食、住、行需要。

3) 响应国家政策，及时调整人口政策。

出生率低是造成老龄化问题的原因之一，提高出生率可以缓解老年人口抚养压力，增加社会工作活力。为进一步优化生育，目前我国已经实施一对夫妻可以生育三个子女的政策，同时出台了相应的配套支持措施。秦皇岛也积极顺应国家要求，针对三孩政策推出了延长产假、增设育儿假等条例。另外实行人才引进计划 [10]，吸引更多年轻人留秦就业，也有利于稳定社会劳动人口年龄结构。

老年型社会的到来对秦皇岛市的经济、卫生、生态等都带来了极大的挑战，应对老龄化问题推行各种政策举措刻不容缓。