应用背景下“高等数学”课程思政若干案例

Some Cases of Ideological and Political Work in the Course of “Advanced Mathematics” under the Background of Application

摘要: 本文围绕应用背景下高等数学课程特点、大学生特点及教师教学特点出发，通过古籍古诗、数学的实际应用、数学思想方法、数学知识结构、数学蕴含的科研思想、数学史、数学解题思路七大方面来挖掘高等数学课程思政案例。以研促教，通过案例挖掘反思高等数学教学应做好六点重视：教研相长，通过高等数学课程思政实践教学帮助我校学生更好的学习数学，并为应用型高校数学教师的高等数学教学提供参考。

Abstract: This paper focuses on the characteristics of advanced mathematics curriculum, the characteristics of college students and the teaching characteristics of teachers. The paper explores the cases of ideological and political work in the course of advanced mathematics by referring to the Chinese masterpieces and poems and using the practical application of mathematics, the method of mathematical thinking, the structure of mathematical knowledge, the scientific research ideas contained in mathematics, the history of mathematics and the thinking pattern of mathematical problem-solving. To promote teaching through research and to reflect on the teaching of Advanced Mathematics through case study, we should pay attention to six points, teaching and research are mutually beneficial, and through ideological and political practice teaching of advanced mathematics course, we can help the students of our university to study mathematics better, it also provides the reference for the Advanced Mathematics Teaching of the Applied University Mathematics Teachers.

1. 引言

人类社会的进步与数学这门科学的广泛应用是分不开的，其中一个重要的原因就是数学是一门偏重于思维训练的学科，学习数学的过程就是思维训练的过程。所以高等数学作为一门基础学科，它在本科教学中有着举足轻重的作用 [1]。应用背景下的高等数学课程、大学生及教师教学的特点有其特殊性，高等数学课程思政的融入需要围绕这些特点出发。

1.1. 应用背景下高等数学课程特点

高等数学作为应用型大学工科类通识课程，每周5~6学时，开设2个学期，上承初等数学，下启学生专业课程，又是学生专升本、考研中的必考科目，对学生的知识体系的搭建有着重大意义和深远影响。《高等数学》这门课的课程特点和教学地位，决定了它在开展课程思政建设工作中的重要地位以及课程思政建设的必要性和重大意义。

高等数学这门课理论性强，抽象度高、难度系数大，这一定程度上阻碍了这门课程中融入思政建设的有效进行和实施。

应用型大学专业设置的培养方案是文理兼招，这就使得同一个班级的学生数学知识储备和接受数学知识的能力参差不齐，因此我们对学生的初等数学能力不能高估。

学生学完高等数学后往往不会应用，这有违应用型大学的人才培养初衷。数学的学习，归根到底是为了解决生活中的问题，对于应用型高校，引导学生更好的明白数学方法的产生以及数学知识在生活生产科技中的应用是非常关键和必要的。

1.2. 应用背景下大学生特点

当代学生面临社会上的各种诱惑，并且对自己不认同的观点有很强的抵触情绪。当学生领悟不到微积分的美妙时，就会抵触高等数学的学习。

当代大学生大多是独生子女，从小被家长溺爱又没有受到良好的劳动锻炼，吃苦耐劳及克服困难的坚强意志有所欠缺，高等数学课程的特点使得很多学生心生畏惧。

通过教学实践了解到学生在高中阶段对数学基础知识的掌握并不扎实。有的学生对初等数学的学习就兴趣不高，再面对高等数学，更是望而却步。

1.3. 应用背景下高等数学教学特点

高等数学教学任务重，多数教师采取“填鸭式”的传统教学模式 [2]，加之高等数学知识容量广，每次课教学密度大，但是教师教学手段相对单一，情景引入相对单调，这也直接或间接地影响了学生的学习兴趣，进而影响了学生的发展。

本文基于以上思考，以我校地球科学与工程学院本科生为研究对象，教材以同济大学第七版《高等数学》(上、下)为例，从教学实践出发，围绕古籍古诗、数学的实际应用、数学思想方法、数学知识结构、数学蕴含的科研思想、数学史、数学解题思路七大方面来挖掘高等数学课程思政案例，力图在不改变高等数学基本知识即“骨架”的基础上，开发思政案例，丰富高等数学的“血肉”，一方面将思政元素应用到教学当中，实现教学相长，教学与科研相统一，为“高等数学”课程的课程思政教学改革提供支撑；另一方面，帮助我校学生更好的学习数学，并为应用型高校数学教师的高等数学教学提供参考。

2. “高等数学”课程思政若干案例

2.1. 古籍古诗相关案例

1) 以极限为例，古诗“落霞与孤鹜齐飞，秋水共长天一色”，“水天一色”，水的极限处是天，带领学生在诗词中感悟数学，体会数学也可以是灵动文艺的，感受中国古典的博大精深。

2) 以函数的极值为例，用古诗“横看成岭侧成峰，远近高低各不同”引入，让学生认识极值是一个局部性的概念，好比我们的人生通过高考达到了局部极大值，而是否为最大值就要从暮年回望我们这一生才能得出结论，所以我们要不断努力，争取每一个人生阶段都收获极大值。

2.2. 数学的实际应用

1) 以极限为例，极限思想本质是一个动态性的过程，可联系到社会经济发展，发展是硬道理，经济问题是在动态发展中解决的。

2) 以定积分的应用为例，提出“洱海海岸线有多长？”这一问题。海岸线的变化是非均匀的，解决就要考虑用“局部均匀化求近似，再利用极限得精确”的思想来解决，实际就是用我们所学的定积分来解决。纵观国家经济，经济发展借助于市场化整为零，国计民生和重大全局项目由国家统筹推进就是积零为整，集中力量办大事。同时，“先富带动后富”就是化整为零，“共同富裕”就是积零为整。

这种问题驱动的教学方式不仅能增加学生运用数学解决生活中实际问题的能力，也是理论与实践相结合的马克思主义哲学观。联系实际意义对应数学知识，让学生从理论中来，到实践中去，真正的把数学的学习放到生活中、专业中去应用。

2.3. 围绕数学思想方法

1) 以映射为例，函数是特殊的映射，认识了一般情形，进而得出特殊情形，即从一般到特殊的思想方法。

2) 以微积分基本公式为例，认识了变速直线运动路程运算结果这一特殊情形，进而得出更一般的牛顿-莱布尼兹公式，即从特殊到一般的思想方法。

3) 数学上有些逻辑关系是不好进行论证的，但是通过举特殊的反例却能更直观的说明递推关系不成立，比如一元函数 $y=\left|x\right|$ 在点 $x=0$ 处连续但是不可导，二元函数 $z=\left|x\right|+\left|y\right|$ 在点 $\left(0,0\right)$ 处连续，但是不可导。举反例也是数学特有的辩证的思想方法。同时，反正法也是数学证明中常用的论证方法。

4) 以级数的比较审敛法为例，涉及了放缩法。

2.4. 数学知识结构

1) 以函数的间断点为例，建构树杈图(如图1)帮助学生从连续的对立面总结出间断点的分类，通俗的呈现知识点，让抽象复杂的内容用最简单、直观的语言或者图形来刻画，既升华了知识点的内涵，也便于学生理解。同时，间断与连续是辩证统一的，通过学习，帮助学生提升辩证思维能力。

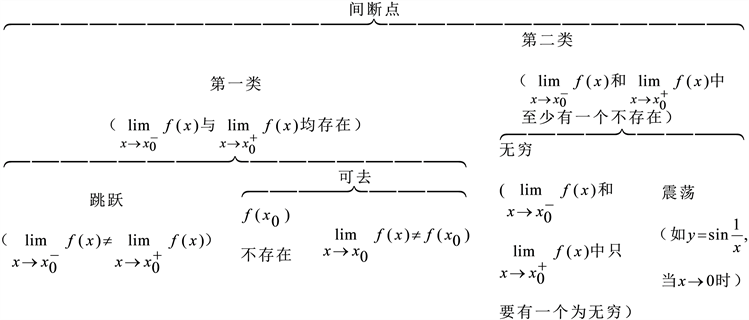
Figure 1. Classification of discontinuous points of function-bifurcation diagram

图1. 函数的间断点分类树杈图

2) 以洛必达法则为例，善于抓住知识点之间的联系(如图2)，对应马克思主义哲学观，抓住知识的本质，即抓住主要矛盾，掌握解决主要矛盾的方式方法，通过转化，次要矛盾也迎刃而解。

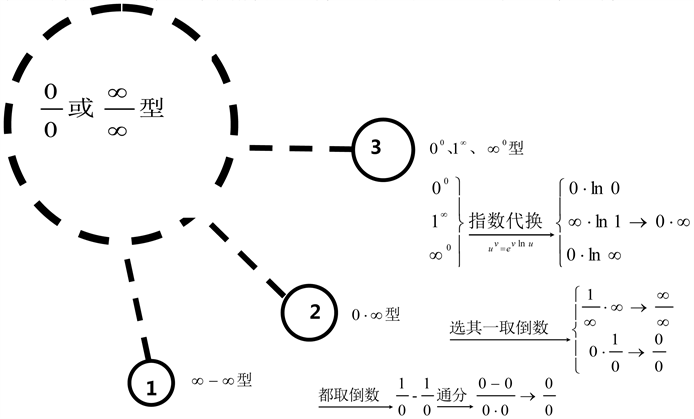
Figure 2. L’Hôpital’s rule involves the transformation and normalization of computing types

图2. 洛必达法则涉及的计算类型的转化与归一图

3) 以一元函数与多元函数可微、可导、连续 [3] [4] 之间的关系图为例(如图3)，教会学生学习要善于类比，又要区别异同。能联系过去，把过去适用的作为现在的基础，又能丰富现在，在原有认识的基础上拔高认知。

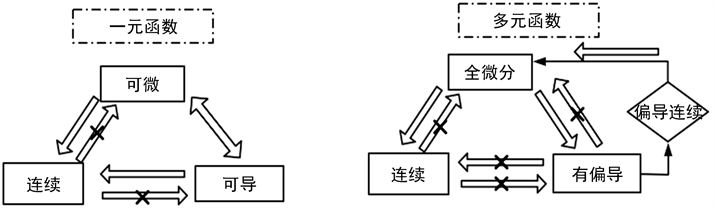
Figure 3. The comparison of the relation between the function of one variable and the function of many variables in three relations

图3. 一元函数与多元函数在三大关系上的联系对比图

2.5. 围绕数学蕴含的科研思想

著名数学家高斯曾说过 [5]：“若无某种大胆果敢的猜想，一般来说是不可能有知识进展的”。以下的课程思政教学案例将围绕猜想设计，抛出“困难”，引导学生思考，恰当给出“发现”，诱导学生“合理猜想”，亦或给出数学家当初的猜想，再展示数学家的证明过程，最后给出完美数学结论。通过这个过程既能潜移默化培养学生科学研究的正确思路和方法，又能带领学生领悟科学的发展历程，养成热爱研究的习惯，进而树立正确的人生观、世界观和价值观。

1) 教学案例1：微积分基本公式

困难：定积分是特定形式的和的极限，即 $\underset{\lambda \to 0}{\lim }{\displaystyle \underset{i=1}{\overset{n}{\sum }}f\left({\xi }_i\right)\Delta x_i}\stackrel{存在}{=}{\displaystyle {\int }_a^{b}f\left(x\right)\text{d}x}$，经过“分割、近似、求和、

取极限”四个步骤得到，不好求解。

发现：变速直线运动的路程 $S=\underset{\lambda \to 0}{\lim }{\displaystyle \underset{i=1}{\overset{n}{\sum }}v\left({\tau }_i\right)\Delta t_i}={\displaystyle {\int }_{T_1}^{T_2}v\left(t\right)\text{d}t}=S\left(T_2\right)-S\left(T_1\right)$，且 $S^{\prime }\left(t\right)=v\left(t\right)$。

思考：是否该特例不是一个偶然而具有普适性，且由上一节易知

${\displaystyle {\int }_0^{1}x{}^2\text{d}x}=\underset{\lambda \to 0}{\lim }{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(\frac{i}{n}\right)}^2}\cdot \frac{1}{n}=\underset{n\to \infty }{\lim }\frac{1}{n^3}\cdot {\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(i\right)}^2}=\frac{1}{3}$，正好等于 $x^2$ 的原函数 $\frac{1}{3}{x}^3$ 在0到1上的增量。

猜想： $f\left(x\right)\in C\left[a,b\right]$， $F^{\prime }\left(x\right)=f\left(x\right)$，则 ${\displaystyle {\int }_a^{b}f\left(x\right)\text{d}x}=F\left(b\right)-F\left(a\right)$。事实上，这就是著名的牛顿-莱

布尼兹公式，也称为微积分基本公式。

辅助定义、定理：想要证明这个猜想，需要定义积分上限函数 $\Phi \left(x\right)={\displaystyle {\int }_a^{x}f\left(t\right)\text{d}t}$，并给出积分上限函

数求导的定理 ${\Phi }^{\prime }\left(x\right)=f\left(x\right)$，得出积分上限函数也是定积分的被积函数的原函数。

证明猜想：用辅助定理证明即可。

思政元素：几千百年来，苹果砸在了无数人的身上，但是只有牛顿开始研究万有引力定律，这就是科学研究精神。我们每一次多一些思考，多做一些事情，也许就会让世界变得不一样。同时，微积分基本定理的出现不是偶然的，是有依据的，但是要严谨的证明还需要提供新的定义及定理。这告诉我们科学的思考方式很重要，用新的方法解决了新的问题就是伟大的创新，这好比用新的花瓶插了新的花朵。

2) 教学案例2：一阶线性微分方程的通解

困难：一阶非齐次线性微分方程 $y^{\prime }+P\left(x\right)y=Q\left(x\right)$ 不易求通解。

发现：一阶齐次线性微分方程 $y^{\prime }+P\left(x\right)y=0$ 通过可分离变量得其通解为 $y=C\cdot {\text{e}}^{{\displaystyle \int -P\left(x\right)\text{d}x}}$。

思考：齐次等式的右边是常数0，非齐次等式的右边是一个关于x的函数，是否其通解就是把齐次通解中的C换成一个关于x的函数。

猜想：一阶非齐次线性微分方程的解为 $y=u\left(x\right)\cdot {\text{e}}^{{\displaystyle \int -P\left(x\right)\text{d}x}}$。这就是常数变易法。

验证：将假设带回方程检验，求出 $u\left(x\right)={\displaystyle \int Q\left(x\right)\cdot {\text{e}}^{{\displaystyle \int P\left(x\right)\text{d}x}}\text{d}x}+C$，这确实是一个关于x的函数。可见这

不仅是非齐次的解，还是非齐次的通解。

思政元素：饭是一口一口吃的，解决问题也一样，先解决了简单的问题，合理对比，合理猜想，再严谨的验证。伟大的数学问题的解决往往带有“柳暗花明又一村”的意境。这个过程也是用已有的方法解决了新的困难，相当于用旧的花瓶插了新的花朵。

3) 教学案例3：高阶线性微分方程的通解

困难：高阶线性微分方程的通解不好求。

发现：一阶线性微分方程的通解有以下结构特征：

$y=\underset{一阶齐次线性通解}{\underset{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}{C\cdot {\text{e}}^{{\displaystyle \int -P\left(x\right)\text{d}x}}}}+\underset{一阶非齐次线性特解}{\underset{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}{{\displaystyle \int Q\left(x\right)\cdot {\text{e}}^{{\displaystyle \int -P\left(x\right)\text{d}x}}\text{d}x}}}$。

思考：二阶线性微分方程的通解是否仍有该结构特征，若有，能否进一步推广到高阶线性微分方程。

猜想：二阶非齐次线性微分方程 $y^{″}+P\left(x\right)y^{\prime }+Q\left(x\right)=f\left(x\right)$ 的特解为 $y^{*}$，对应的二阶齐次线性微分方程 $y^{″}+P\left(x\right)y^{\prime }+Q\left(x\right)=0$ 的通解为Y，则 $y=Y+y^{*}$ 为所给二阶非齐次线性微分方程的通解。且高阶线性微分方程也有该解的结构。

辅助定理：

定理1 [3]：当 $y_1\left(x\right),y_2\left(x\right)$ 是微分方程 $y^{″}+P\left(x\right)y^{\prime }+Q\left(x\right)=0$ 的两个特解时， $Y=C_1{y}_1+C_2{y}_2$ 也是该微分方程的解。

鉴于Y并不一定是该微分方程的通解，进一步定义线性相关与线性无关的概念。

定理2 [3]：当 $y_1\left(x\right),y_2\left(x\right)$ 是微分方程 $y^{″}+P\left(x\right)y^{\prime }+Q\left(x\right)=0$ 的两个线性无关的特解时， $Y=C_1{y}_1+C_2{y}_2$ 也是该微分方程的通解。

验证猜想：将 $y=Y+y^{*}$ 带回二阶非齐次微分方程进行验证，发现该通解结构适用于二阶线性微分方程。同时，可推广到高阶线性微分方程。

思政元素：数学之所以美的一个原因在于它的辩证法，辅助定理1很容易让我们觉得Y即为通解。但是事物是发展变化的，矛盾是事物发展变化的源泉和动力，数学概念的每一次扩展无一不是解决矛盾的过程。定义了线性无关，辅助定理2完美的推进了定理1。这个问题相当于用新的瓶子来插已有的花。

4) 教学案例4：已知物体做变速直线运动，其运动规律为 $S=S\left(t\right)$，求物体在某一时刻 $t_0$ 处的瞬时速度 [3]。

困难：在知道路程与时间的关系式下求速度，而且是变速直线运动。

已有经验：若为匀速直线运动，则 $\bar{v}=\frac{\Delta S}{\Delta t}=\frac{S\left(t_0+\Delta t\right)-S\left(t_0\right)}{\Delta t}=v_{t_0}$。

思考：当时间改变量 $\Delta t$ 越小， $\bar{v}$ 就越接近于瞬时速度 $v_{t_0}$。

辅助定义：函数 $f\left(x\right)$ 在点 $x_0$ 的某去心邻域内有定义，当x越来越接近 $x_0$ 时，函数 $f\left(x\right)$ 越来越接近

于常数A，则记 $\underset{x\to x_0}{\lim }f\left(x\right)=A$。称常数A为函数 $f\left(x\right)$ 在 $x\to x_0$ 下的极限 [3]。

结论：当 $\Delta t$ 越来越接近于0时，有 $\underset{\Delta t\to 0}{\lim }\bar{v}=v_0$，即 $\underset{\Delta t\to 0}{\lim }\frac{\Delta S}{\Delta t}=v_0$。

思政元素：生活中，交警查车辆违章就是应用了这个思想，短时间内快速的抓拍两张汽车行驶照片，即有了时间的改变量与路程的改变量，就可以测算该车辆是否超速。数学的伟大在于它源于生活，应用于生活而又高于生活。我们的研究为的就是能解决一些原来解决不了的问题，通过研究让我们的生活过得更好这是我们社会主义接班人应有的人生追求。

2.6. 围绕数学史

1) 以极限为例，介绍“刘徽割圆术”的思想方法，引出我国早期就有的极限思想，增加民族自豪感。

2) 以微分中值定理为例，认识数学家费马、罗尔、拉格朗日、柯西的同时，学习他们身上对科学孜孜不倦的探索精神。

贯穿数学史，带领学生领略科学研究精神及数学的有趣发展历程。特别在我们引入新的知识点时，讲明是什么问题背景引起的知识点诞生是很重要的，这不仅能增加学生学习数学的兴趣，也能增加学生勇于思考问题、积极解决问题的能力。

2.7. 围绕数学解题思路

1) 以计算该极限

$\underset{n\to \infty }{\lim }\left(\frac{1}{\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+2}}+\cdots +\frac{1}{\sqrt{n^2+n}}\right)=1$

为例，这是无穷多个无穷小相加，结果却不是无穷小，这不仅体现了“勿以善小而不为”的儒家思想，又体现了“滴水穿石”及“量变到了一定程度就能引起质变”的哲学观，鼓励学生要学会坚持。

2) 以计算该三重积分 ${\displaystyle \underset{D}{\iiint }z\text{d}x\text{d}y\text{d}z}$ 为例，其中D是由曲面 $z=x^2+y^2$ 与平面 $z=4$ 所围的闭区域。根据

三重积分的计算法，本题既可以采用柱坐标计算又可以采用截面法计算，用柱坐标计算过程中，仅是把坐标系换为柱面坐标系，采用的本质方法是投影法，而显然用“先二后一”比“先一后二”更好计算。这不仅体现了我们只有努力了，能力达到了相应标准，我们才有选择的权利，同时，也表明选择很重要，更恰当的选择能帮助我更快捷的到达彼岸。

3) 以计算二重积分 ${\displaystyle \underset{D}{\iint }{\text{e}}^{-y^2}\text{d}x\text{d}y}$ 为例，其中D是以 $O\left(0,0\right),A\left(1,1\right),B\left(0,1\right)$ 为顶点的三角形闭区域 [4]。根

据二重积分的计算，因为函数 ${\text{e}}^{-y^2}$ 的原函数不是初等函数，所以本题用直角坐标系下的X型无法解决，但用Y型却能得到“豁然开朗”的结果。这也说明，我们遇到困难要有百折不挠的精神，不是这个方法不行了就放弃思考，否则问题永远解决不了，生活中的问题也一样，不主动去解决，问题就像滚雪球会越滚越大，多一些耐心，多一些努力，转换一下思路，问题就能解决，我们数学的解题思路与我们的个人成长一样，也应该是一个螺旋式的上升过程；当然，本题若用极坐标，由于极坐标系下积分区域为

$D=\left\{\left(\rho ,\theta \right)|0\le \rho \le \frac{1}{\sin \theta },\frac{\pi }{4}\le \theta \le \frac{\pi }{2}\right\}$，计算过程冗长；而格林公式的给出，告诉我们二重积分还可以用

第二类曲线积分进行计算，通过恰当选择 $P\left(x,y\right),Q\left(x,y\right)$ 便能很快得到结果。可见，格林公式是一个伟大的创新，它将二重积分和曲线积分之间建立了完美联系，这种创新的精神值得我们学习借鉴。同时由后边的学习可以知道，高斯公式建立了三重积分与曲面积分之间的关系，斯托克斯公式又进一步建立的曲面积分与曲线积分的关系，从三个公式的结构来看，也可以给我们很多科研的思路。

以上案例都是通过极其普通的数学题，渗透其中蕴含的为人处世的道理。而解决数学题的过程，既要不怕麻烦，又要有纵观全局择最优方法的能力，这既能培养学生直面困难、勇于挑战、全局考虑、慎重选择的思维品质，又能加强学生的逻辑思维能力，增强学生的学习能力及自我认知能力。

3. 高等数学课程思政案例反思

应用背景下的高等数学课程、大学生及教师教学有其独特性，通过案例挖掘及实践，笔者反思到高等数学教学中，我们要做好以下六点重视：

第一，重视诱发猜想，激发学生求知欲望。只有打开学生想象的空间，才能帮助学生更好的创新。波利亚曾指出“教学必须为发明作准备，或者至少给一点发明的尝试，无论如何，教学不应该压抑学生中间的发明萌芽 [6]。”我们数学教师在教学中，要恰当设计教学过程，帮助学生合情合理进行猜想。

第二，重视问题驱动教学。亚里士多德说“思维自疑问和惊奇开始” [7]，高等数学就是一门以问题驱动教学的课程。教师教学，不仅要注重问，还要精心设计“问题”，让每个问题都问出质量。高等数学的教学需要我们点燃学生的好奇心，需要我们培养学生发现问题解决问题的科学研究精神。

第三，重视数学史、数学名人的介绍，没有一种知识是无缘无故产生的。数学的学习离不开数学史，我们都是站在“巨人”的肩膀上学习的，就要了解“巨人”的故事，从名人轶事中学习科学研究方法，感悟科研精神力量。通过课程思政中数学史的融入，高等数学就犹如活水，有了来源。好比牛顿，既是数学家又是物理学家，他在研究物理问题时候遇到了困难，转而开始研究数学，这就是伟大的科研精神。

第四，重视挖掘数学理论最原始最火热的思考。国际数学教育委员会前主席，荷兰数学家H. Freudenthal有句很有启发性的名言：“没有一种数学思想，以他被发现时的那个样子发表出来，一个问题被解决以后，相应的发展成一种形式的技巧，结果使得火热的思考变成了冰冷的美丽 [8]。”高等数学集完美的微积分理论于一体，但是没有给出理论最原始的思考历程，对学生而言这就是冰冷的，所以需要我们教师去帮助学生挖掘出这些火热的思考，带领学生习得正确的科研方法及提升学生学习数学的兴趣。

第五，重视帮助学生从结构上理解数学知识。布鲁纳认为：不论我们教什么学科，务必使学生理解该学科的基本结构。数学作为一门基础学科，对其知识结构的理解能够很好的帮助学生学习。通过课程思政中知识结构的融入，高等数学知识模块更加清晰，学生不仅能掌握高等数学的“骨架”，还能从“骨架”联系到“血肉”。这是一个把高等数学书读厚再到读薄的过程。同时也可为部分考研学生打下扎实的数学基础。

第六，重视教学结合实践，数学是一门工具性学科，为了达到学以致用的目的，教学必须与学生的专业应用相结合。可以通过恰当引入学生专业中的简单例子，帮助学生习得将数学应用于专业的能力，这才能与应用型大学培养应用型人才的初衷吻合。

4. 结语

本文通过对应用背景下高等数学、大学生、教师教学的特点分析，挖掘了七大方面的课程思政案例，并在实践教学中做出了六点反思。但是，高等数学课程思政远不止于此，我们既可以继续丰富以上已有的每个大方面下的小案例，也可以继续挖掘其他方面的高等数学课程思政案例，最终形成应用背景下的高等数学课程思政案例库、课件库等。同时，为了能更好的在高等数学课程中融入课程思政，应用背景下的高等数学教学模式也需要进一步改革与实践。

基金项目

应用背景下的高等数学课程思政建设(21KC06)，《高等数学》金课建设(21JK11)。