一种空气弹簧的动力特性分析

Dynamic Characteristic Analysis of an Air Spring

摘要: 空气弹簧有着优越的振动控制效果，本文建立了带辅气室的空气弹簧简化模型，利用热动力学、流体力学的基本原理，求解了不同孔径参数下的振动传导特性，讨论了气室容积比对系统阻尼比的影响。结果表明连管孔径对空气弹簧垂向力学特性影响较大，连管孔径越大，空气弹簧系统振动传导率峰值越小，固有频率越小；空气弹簧系统阻尼比随容积比的增加而增加，当容积比超过一定值后，弹簧阻尼不再快速变化；选择合适的孔径和容积比参数可有效调节振动传导，提高空气弹簧的性能。最后建立了空气弹簧的三维模型进行仿真分析。

Abstract: Air spring has a superior vibration control effect. This paper establishes a simplified model of air spring with auxiliary volumes. By using the basic principles of thermal dynamics and fluid mechanics, the vibration transmissibility characteristics of the different parameters of the pipeline have been solved, and the gas chamber volume ratio on the system damping ratio has been discussed. The results show that the diameter of the connecting tube has a great influence on the vertical mechanical properties of the air spring. The larger the diameter of the connecting pipe is, the smaller the peak value of the vibration conductivity of the air spring system is, and the smaller the natural frequency is. The damping ratio of the air spring system increases with the increase of the volume ratio, but when the volume ratio exceeds a certain value, the spring damping does not change rapidly. Selecting the appropriate aperture and volume ratio parameters can effectively adjust the vibration conduction and improve the performance of the air spring. Finally, the three-dimensional model of air spring is established for simulation analysis.

1. 引言

空气悬架系统(如图1所示)是以空气弹簧(如图2所示)为弹性元件，利用气体的可压缩性实现其弹性作用的一种悬架，可以大大提高运载效果和乘坐的舒适性。空气弹簧是一种非金属弹簧，由有帘线的橡胶囊和充入其内腔的压缩空气等非金属弹性元件所组成，按形状可分为囊式、膜式和袖筒式空气弹簧三大类，其中囊式空气弹簧是较为常见的一类，如图2所示。

Figure 1. The suspension with air spring

图1. 空气悬架

Figure 2. The air spring

图2. 空气弹簧

与传统线性弹簧相比，空气弹簧具有承载能力强、非线性特性好、刚度可调、阻尼特性优良、固有频率可调、隔音性能好、重量轻等特性，主要表现为：高度和内部气压可随时调节、可根据需要设计理想的特性线、吸收高低频振动和降噪的性能、刚度可以通过附加气室的容积和有效面积来进行改变、自振频率很低而且基本不变、空气弹簧主气室和附加气室之间有一节流孔或管路，通过改变节流孔的孔径和管路直径、长度可以达到最佳的阻尼系数 [1]。

空气弹簧的振动传导特性是决定空气悬架系统性能的关键，其振动传导特性主要通过刚度、固有频率、阻尼特性等参数进行表征。通过调节空气弹簧内压和体积可达到空气弹簧刚度调节的目的，也可以通过增加辅助气室的方式调节空气弹簧的刚度。在承载能力不变的前提下，空气弹簧可以通过改变自身刚度的大小来调整系统固有频率 [2]。

目前，国内外对空气弹簧系统进行振动特性计算的研究较少。Lee [3] 等人将空气弹簧的体积和有效面积近似表示为位移的三次多项式，建立空气弹簧静刚度模型，并通过实验进行验证。Zhu [4] 构建了一个空气弹簧模型，其中粘性阻尼是速度指数，这个指数的数值是1.8。2012年陈寒霜利用非线性有限元理论和方法对空气弹簧垂向弹性特性进行了理论分析、试验研究和仿真计算，建立了空气弹簧座椅悬架系统单自由度仿真模型 [5]。王家胜等建立了带附加气室空气弹簧系统的动力学方程，经过线性化处理后推导出系统的复刚度模型，建立了系统的等效刚度、等效阻尼及固有频率计算模型 [6] [7] [8]。2018年于航、姚国凤 [9] 等运用有限元分析方法开展了低温环境对空气弹簧静力学特性的研究。2018年祝恒佳、张云青 [10] 等人提出幅变、频变非线性空气弹簧的动力学模型，提出了改进的Berg摩擦模型并进行了实验。2021年尹航、邬明宇等人 [11] 结合复合材料特性及空气弹簧的几何结构，提出了膜式空气弹簧有效面积计算的理论公式，并进行了实验验证。

本文将从悬架系统出发，建立空气弹簧简化模型(带辅气室)，利用动力学方程，分析节流孔直径和气室容积比对空气弹簧振动特性的影响规律。

2. 计算模型

空气弹簧是由帘线层、内外橡胶层或钢丝圈经成型后形成的一种密封曲形胶囊，通过向其中充入压缩空气形成压缩空气室，从而实现隔振和缓冲作用的非金属弹簧。内胶层起密封作用，外胶层除了密封作用之外还能起到保护帘布层的作用。一般来说空气弹簧由上底座、下底座和缓冲垫经装配后形成的具

Figure 3. Computation model

图3. 计算模型

有密封气室的整体。本文选用常用的双曲囊式空气弹簧进行简化分析，双曲囊式空气弹簧主要分为主气室、附加气室、节流孔和活动底座组成，对其进行简化，如图3所示，以便于建立计算模型。

以一种带附加气室的双曲囊式空气弹簧为对象，利用热动力学、流体力学的基本原理建立计算模型。为简化计算模型，假定：

1) 空气弹簧内的气体是理想气体；

2) 弹力作用区域面积保持不变；

3) 热传递发生在弹簧和它的周围

4) 由粘弹性表示弹簧材料的未知阻尼；

5) 空气弹簧内的气体符合流体方程和质量守恒定律。

在实际工况下，辅气室与主气室间有气体流动，当空气弹簧受压时，气囊开始受压变形，得益于上下两个气室的形状和参数设计，气室间产生压差，气体在两个气室间产生流动，假设气体的流动是连续的，则可定义 [4] [5] [6]：

$\frac{\text{d}{m}_1}{\text{d}t}=-\stackrel{\dot{}}{m}=-\frac{\text{d}{m}_2}{\text{d}t}$ (1)

式中 $\stackrel{\dot{}}{m}$ 、 $m_1$ 、 $m_2$ 分别是气体质量流动率及上下气室空气质量。

橡胶在收缩和膨胀过程中气流摩擦会导致能量的损耗，使得动能转化为热能，从而实现空气弹簧的吸能减振功能，能量损耗主要由达西–韦史巴赫方程决定：

$P_l\left(t\right)=f_l\frac{l}{d}\frac{V{\left(t\right)}^2}{2g}$ (2)

式中P_l是气体内部摩擦能量耗散量，f_l是摩擦系数，d是连管直径，l是连管长度，V是流速，g是重力加速度。

其中摩擦系数与空气本身的粘度和管壁的粗糙度相关：

$f_l={\left(-0.86\ln \frac{e}{3.7d}\right)}^{-2}$ (3)

式中e是管壁粗糙度，空气粘度参数由常系数表达。

利用管道流体能量方程并考虑流体摩擦有效面积可获得：

$\stackrel{\dot{}}{m}\left(t\right)=\frac{\left(\pi /4\right)d^2\sqrt{2\frac{P_1\left(t\right)+P_2\left(t\right)}{R\left(T_1\left(t\right)+T_2\left(t\right)\right)}\left|P_1\left(t\right)-P_2\left(t\right)\right|}}{\left(1/d\right)\sqrt{f_l}+K_C+K_E}+K_X\mathrm{sgn}\left(P_1\left(t\right)-P_2\left(t\right)\right)$ (4)

式中T是温度，K_C和K_E分别是收缩耗散系数和膨胀耗散系数，K_X是管道摩擦耗散系数。

空气弹簧使用过程中，气体温度变化率方程：

${\stackrel{\dot{}}{T}}_1\left(t\right)=\frac{A_1{P}_1\left(t\right){\stackrel{\dot{}}{x}}_1\left(t\right)-C_p{T}_1\left(t\right)\stackrel{\dot{}}{m}\left(t\right)+Q{A}_{s1}\left(t\right)\left(T_{s1}-T_1\left(t\right)\right)}{m_1\left(t\right)C_v}$ (5)

式中Q是热交换系数，A是管壁面积，C_p和C_v分别是恒压比热和恒容比热。

将温度变化率方程和流体质量变化率方程代入到压力方程，并利用理想气体方程：

${\stackrel{\dot{}}{P}}_1\left(t\right)=-\left(1+\frac{R}{C_v}\right){\stackrel{\dot{}}{x}}_1\left(t\right)\frac{P_1\left(t\right)}{x_1\left(t\right)}-\left(1+\frac{C_p}{C_v}\right)\stackrel{\dot{}}{m}\left(t\right)\frac{P_1\left(t\right)}{m_1\left(t\right)}+\frac{2R}{r_1{C}_v}Q\left(T_a-T_1\left(t\right)\right)$ (6)

式中R是气体常数。

对于辅气室，忽略掉热交换后同样有：

${\stackrel{\dot{}}{P}}_2\left(t\right)=\left(1+\frac{C_p}{C_v}\right)\stackrel{\dot{}}{m}\left(t\right)\frac{P_2\left(t\right)}{m_2\left(t\right)}$ (7)

定义空气弹簧系统的振动传导率：

$TR\left(frequency\right)=\frac{\max Z}{\max Z^{\prime }}$ (8)

式中Z和 $Z^{\prime }$ 分别是激励幅值和响应幅值。可以联立上述公式求解。

3. 算例

按照常用空气弹簧参数及经验参数对算例中的各参数进行取值，如表1所示。其中上气室管壁面积A₁，上气室上盖板位移x的初始值为0.08 m，温度T初始值为290 K，上气室空气质量为30 kg，气体初始流速c = 400，气体常数R = 280，重力加速度g = 9.8，热交换系数Q，下气室气体体积V₂初始值为0.0008 m³，连管长度l = 0.03 m，气体压强P初始值为160e3Pa，管壁粗糙度e = 0.005，收缩耗散系数K_C = 0.5，膨胀耗散系数K_E = 1.1，管道摩擦耗散系数K_X = 1，根据上文公式得到不同直径下振动传导率随频率变化的变化曲线。

当节流连管直径d分别取1、2、5 mm时，振动传导率随频率变化的变化曲线如图4所示，当d = 1 mm时，其振动传导率峰值为3.5，固有频率为3.25 Hz，当d = 2 mm时，其振动传导率峰值为2.75，固有频率为3 Hz，当d = 5 mm时，其振动传导率峰值为2.25，固有频率为2.25 Hz，可发现节流连管直径越大，空气弹簧系统振动传导率峰值越小，固有频率越小。这主要是由于连管直径大小对系统刚度和阻尼均有明显影响，连管直径增大，空气弹簧刚度减小，系统阻尼比先增大后减小，进而固有频率减小，振动传导率峰值减小。

当容积比(上气室气体体积V₁/下气室气体体积V₂)变化时，系统阻尼比变化曲线如图5所示，可以发现容积比从0增加到8，系统阻尼比从0.15增加到0.4，但增大速率随着容积比的增加而缓慢减低，容积比超过8时，系统阻尼比增大速率降低为0，系统阻尼比几乎不再增加。因此在一定范围内系统阻尼比随容积比的增加而增加，超过此范围系统阻尼比基本不变。

4. 仿真模型

本文建立了空气弹簧的简单三维模型，并利用有限元分析原理进行仿真分析。根据算例中的数值建立了模型，三维模型如图6所示。图7为模型的横截面显示。

Table 1. The parameter value

表1. 算例中各参数取值

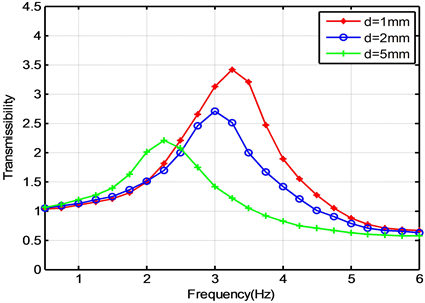
Figure 4. The transmissibility of 3 pipe diameters

图4. 3种孔径下的振动传导率

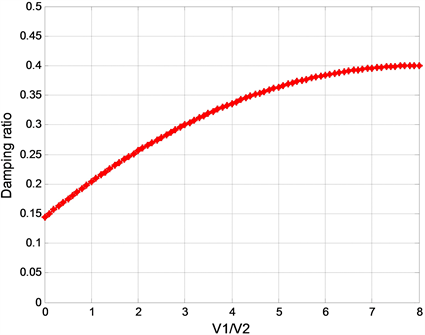
Figure 5. The curve of damping ratio-volume ratio

图5. 阻尼比–容积比曲线

Figure 6. 3D model of air spring

图6. 空气弹簧的3D模型

Figure 7. The cross section of the model

图7. 横截面模型

Figure 8. The deformation of the response amplitude

图8. 响应幅值云图

Figure 9. The cross section of the deformation

图9. 变形截面图

节流连接管直径D为5 mm，输入激励幅值为10 mm。通过模态分析计算出此时其固有频率为2 Hz，响应幅值为4.8 mm。响应幅值的变形如图8所示。图9为变形截面。

根据上一节的理论计算公式，可以得到此时的振动电导率为10/4.8 = 2.08，由上一节理论计算得到的振动电导率曲线可知，仿真计算出的数值与理论计算非常接近。仿真结果也验证了理论计算的准确性和可行性。

5. 结论

理论计算结果表明，带附加气室的空气弹簧减振吸能能力明显提升，通过连管孔径设计，可实现刚度和固有频率的精确调节，从而避免共振带来的负面影响。连管直径对其垂向力学特性影响较大，连管直径越大，空气弹簧系统振动传导率峰值越小，固有频率越小，容易与外界产生共振，但可以获得较好的阻尼效果；连管直径越小，系统刚度越大，固有频率越高，虽然可有效避免与外界共振，但阻尼特性又相对较差，因此，调节连管直径大小对空气弹簧性能至关重要，根据实际应用的功能要求，后续研究可通过参数优化设计获得较好的孔径值。

空气弹簧系统阻尼比随容积比的增加而增加，当容积比超过一定值后，弹簧阻尼不再快速变化，这说明附加气室的作用并不随着设计体积增大而无限上升，在考虑生产成本和产品外形限制的情况下，可根据具体需要设计较为合适的附加气室。

仿真结果在一定程度上验证了理论计算的准确性和可行性。未来我们可以尝试通过仿真模型进行更深入的研究。